Curriculum Builder Portal 2/11/10 9:26 AM
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

La Situation Économique Retient L'attention
Le journal lu par 95% de la population qu'il dessert ! À L’INTÉRIEUR Éthanol...........HA3Pensée Pensée Accident : deux blessés.........HA05Pensée Les Élans termi- nentPe 3e........HA28nsée Vol. 30 No 46 Hearst On ~ Le mercredi 8 février 2006 1,25$ + T.P.S. Dame Nature s’est déchaînée dimanche et lundi, laissant plus de 30 centimètres de neige sur son pas- PenséePensée sage. Les vents violents ont également compliqué la tâche des piétons et des automobilistes. Plusieurs personnes, dont Yvon Grenon, ont dû avoir recours Celui qui apprend les règles à leur pelle hier matin pour nettoyer. Photo Le Pensée Nord/CP de sagesse sans y conformer sa vie est semblable à un homme qui labourerait son champ sans l’ensemencer. Proberbe persan Le directeur d’un asile de fous a deux perroquets: un rouge et un vert. Un jour, ils s’échappent et vont se percher dans un arbre. Le directeur demande si un des patients peut grimper dans l’ar- bre. Un fou se présente, monte dans l’arbre et ramène le perroquet rouge. Ensuite, il va s’asseoir. Le directeur lui demande pourquoi il ne va pas chercher le perroquet vert. Le fou lui répond : - Comme il n’est pas mûr, je l’ai laissé sur l’arbre ! Discours du maire La situation économique retient l’attention HEARST (FB) – La situation À une question à propos d’un la rue Prince, entre les 3e et 6e - le remplacement des planchers économique est un des sujets qui projet de porcherie dans la rues; au Centre récréatif. 6 a retenu l’attention lors du dis- région, le maire Sigouin a indi- - la construction du nouveau che- Par ailleurs, la sécheresse de MERCREDI cours inaugural du maire Roger qué qu’on procédait à une étude min industriel pour détourner la l’été dernier a forcé l’installation Sigouin, dimanche. -
Program Guide Report
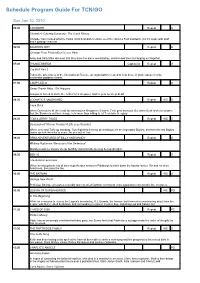
Schedule Program Guide For TCN/GO Sun Jan 10, 2010 06:00 CHOWDER Repeat G Chowder's Catering Company / The Catch Phrase Chowder has created what he thinks is his best dish creation ever! He calls it a Foof sandwich, but it's made with stuff that's garbage material. 06:30 SQUIRREL BOY Repeat G Stranger Than Friction/Don't Cross Here Andy and Salty Mike discover that they have the same weird hobby, which leads them to hanging out together. 07:00 THUNDERBIRDS Captioned Repeat G Cry Wolf Part 2 Follow the adventures of the International Rescue, an organisation created to help those in grave danger in this marionette puppetry classic. 07:30 CAMP LAZLO Repeat G Sweet Dream Baby / Dirt Nappers Lumpus is forced to invite the Jellies for a sleepover and he gets no sleep at all! 08:00 LOONATICS UNLEASHED Repeat WS G Cape Duck When Duck takes all the credit for catching the Shropshire Slasher, Tech gets annoyed. But when Duck starts to suspect that the Slasher is out for revenge, he's more than willing to let Tech take the glory. 08:30 TOM & JERRY TALES Repeat WS G Sasquashed/ Xtreme Trouble/ A Life Less Guarded When Jerry and Tuffy go camping, Tom frightens them by pretending to be the legendary Bigfoot, but then the real Bigfoot teams up with the mice to scare the wits out of Tom. 09:00 GRIM ADVENTURES OF BILLY AND MANDY Repeat G Waking Nightmare / Because of the Undertoad Mandy needs her beauty sleep, but Billy risks his hide to keep her up all night. -

Sydney Program Guide
12/13/2019 prtten04.networkten.com.au:7778/pls/DWHPROD/Program_Reports.Dsp_ELEVEN_Guide?psStartDate=15-Dec-19&psEndDate=2… SYDNEY PROGRAM GUIDE Sunday 15th December 2019 06:00 am Toasted TV G Want the lowdown on what's hot in the playground? Join the team for the latest in pranks, movies, music, sport, games and other seriously fun stuff! Featuring a variety of your favourite cartoons. 06:05 am The Amazing Spiez (Rpt) G Killer Condos Sharky, a top real estate agent, decides to eliminate his competition by selling them his Condos. The Spiez are sent to investigate the disappearances, but find themselves facing a shark. 06:30 am Cardfight!! Vanguard G: Girs Crisis G Shion Vs. Ace (Rpt) After getting stronger through the G Quest, Shion lures Ace out for a fight in the hope of regaining the Kiba family fortune. 06:55 am Toasted TV G Want the lowdown on what's hot in the playground? Join the team for the latest in pranks, movies, music, sport, games and other seriously fun stuff! Featuring a variety of your favourite cartoons. 07:00 am Cardfight!! Vanguard G: Next (Rpt) G Evil Eye Sovereign Enishi, the last remaining member of Team Jaime Flowers, goes up against Onimaru. 07:25 am Toasted TV G Want the lowdown on what's hot in the playground? Join the team for the latest in pranks, movies, music, sport, games and other seriously fun stuff! Featuring a variety of your favourite cartoons. 07:30 am Transformers: Robots In Disguise (Rpt) G The Golden Knight An ancient Cybertronian signal sends Bumblebee and chivalry-obsessed Fixit, to a remote English island for a routine scouting mission that quickly turns into the duo's very own call to adventure. -

LAW and ORDER SPECIAL VICTIMS UNIT "CREDIT" by Matt Sheppo
LAW AND ORDER SPECIAL VICTIMS UNIT "CREDIT" By Matt Sheppo Matt Sheppo [email protected] WGA Registered M. SHEPPO LAW AND ORDER SPECIAL VICTIMS UNIT “CREDIT” TEASER FADE IN: INT. THAD AND BARRY’S APARTMENT - NIGHT THAD, a preppy looking guy in his 20s, stands in his kitchen, perturbed by a smell in the air. He opens a cabinet under the sink and grabs a bag of trash. He sniffs it. THAD Christ, Barry... (calling) Barry! He heads through the bland, middle class apartment, arriving at: BARRY’S ROOM Entering the open door, Thad looks down at BARRY, a large, unkempt man strewn across the floor. PSYCHEDELIC MUSIC plays trough a stereo. THAD Barry, please, if all you’re gonna eat is tuna, disgusting by the way, throw the empty-- Barry? Thad nudges the unmoving Barry with his foot. Nothing. He bends down to get a closer look, putting his finger tips under Barry’s oily nostrils. Again, nothing. He turns Barry’s head to the side and a frothy white substance drains out of his mouth, down his cheek. THAD (CONT'D) Oh Jesus, Barry. Barry!! Suddenly, Barry lets out a stuttered HICCUP and rolls over. There is a bong underneath him, the water soaking the floor. A content smile comes to Barry’s lips. Thad shakes his head. CUT TO: EXT. APARTMENT BUILDING ALLEY - NIGHT Thad opens a dumpster lid and tosses the trash bag inside. As he’s about to close the lid, he does a double take. He looks in the dumpster, flinching in fear. M. -

APA Student Guide
APA Student Guide Centre for Applied Arts & Sciences September 2020 https://lethbridgecollege.ca/document-centre/forms/apa-style-guide/apa-guide Course Writers: Andrew Derksen, Amy Hodgson-Bright, Carolyn Ethier, Rylan Spenrath, Jonathan Davies, Silvana Campus, Judas Bialik Formatter: Amber Bagu Produced by: Centre for Applied Arts and Sciences, Centre for Teaching, Learning & Innovation, Lethbridge College © September 01, 2020 Lethbridge College No part of this manual may be reproduced or stored in any form (now or in the future), including photocopying (unless otherwise indicated) without the prior written consent of Lethbridge College. All rights reserved. Lethbridge College Attn: Intellectual Property Office 3000 College Dr. South Lethbridge, Alberta, Canada, T1K 1L6 Telephone: 403.320.3202, ext. 5506 Care has been taken to trace ownership of copyright material contained within this publication. Lethbridge College welcomes any information that will allow us to rectify any reference or credit for subsequent editions. All requests, concerns, or inquiries regarding copyright should be directed to the Intellectual Property Office at the address above. For permission to use material credited to another source, please direct your request to the appropriate source. This product/publication may include material used under “fair dealing.” Reproduction and communication of this material is allowed by Exceptions in Canadian copyright law, also known as Users Rights, such as section 29, Fair Dealing and Educational Exceptions including section 30.04, Work That is Available Through the Internet. Acknowledgements Thank you especially to the teams in the Learning Café, Learning Services, the Buchanan Library, CTLI, and CAAS. Thanks also to faculty who have provided feedback on the student guide in recent years: Teri Dyck, Kirsten Fantazir, Cheryl Meheden, Brad Keim, Cindy Wilmore, Cathy Takeda, and many faculty members in CAAS. -

5.00 #216 October/November 2008
$5.00 #216 OCTOBER/NOVEMBER 2008 New Books from Hanging Loose Press Tony Towle Sharon Mesmer Michael Cirelli William Corbett Winter Journey The Virgin Formica Lobster with Ol’ Opening Day Raves from his last “At turns intimate or Dirty Bastard A large new collection collection: Tony Towle boisterously satiric, “Vital and eye- of poems. Of past is “one of the New York The Virgin Formica catching and new.” – books: “Taut, School’s best-kept can gently detonate or David Lehman. precise...lucid and secrets.” – John erupt, carrying “Shows how hip-hop unflinching...” – Siri Ashbery. “Tony Towle’s readers along on is the evolution of Hustvedt. “One of the is one of the clear, ripples or classic poetry.” – few poets of our time authentic voices of shockwaves.” – Paul Kanye West. “Tender, who attends so well to American poetry.” – Violi. tough, revelatory...a the ear.” – Library Kenneth Koch. “Smart Praise for previous voice that doesn’t Journal. “Corbett is and sly, sure to disarm work: “. beautifully seem to have occurred interested in the and delight.” – Billy bold and vivaciously before.” – Patricia moment of clarity – Collins. His twelfth modern.” – Allen Smith. First revelation – and lets collection. Ginsberg. collection, by the the force and nature Paper, $16. Hardcover, Paper, $16. director of Urban of ‘seeing’...generate $26. Hardcover, $26. Word NYC. shapes in language.” – August Kleinzahler. Indran Marie Carter Paper, $16. Hardcover, $26. Paper, $16. Amirthanayagam The Trapeze Hardcover, $26. The Splintered Diaries R. Zamora Face: Tsunami Linmark Poems First book from the And keep in mind – editor of Word Jig: New The Evolution of a “These poems both Fiction from Scotland. -

Ask the Expert: Bush's 'Seinfeld' Strategy Michael
Ask the expert: Bush’s ‘Seinfeld’ strategy Michael Fullilove Financial Times www.ft.com 5 April 2007 “In recent times US grand strategy has been guided by a new kind of doctrine, named after not its author but its exemplar: the Costanza doctrine”, writes Michael Fullilove, director of the global issues programme at the Lowy Institute for International Policy in Sydney. “This doctrine”, argues Mr Fullilove, “recalls the classic episode of the TV comedy Seinfeld, “The Opposite”, in which George Costanza temporarily improves his fortunes by rejecting all the principles according to which he has lived his life and doing the opposite of what his training indicates he should do.” Mr Fullilove believes that the Iraq policy pursued by the Bush administration satisfies the Costanza criterion because it is the opposite of every foreign policy the world has ever met. “The Costanza doctrine is all about hope“, he writes, “but when it comes to making your way, in New York or the world, experience is the better guide.” FT.com readers were invited to post their questions on Bush the Costanza doctrine to Mr Fullilove. He answers appear below. ............................................................................................................................................ Q: Isn’t it more accurate to equate the Bush Administration’s Iraq policy to the Seinfeld episode (The Pez Dispenser) where George Costanza needed a hand in his relationship with women? George Bush thought an easy win in Iraq would give the US the upper hand with North Korea and Iran. Instead, the failures in Iraq have left the US, like George Costanza, with no hand at all. Ray Betzner, Philadelphia, US Michael Fullilove: There’s no question that for the ultra-conservatives even more than the neo- conservatives, one of the attractions of the Iraq war was the demonstration effect it would supposedly have. -

Bridge Over Troubled Concrete
NEW SENIOR CENTER OFFERS POOL MEMBERSHIPS! PAGE 13. •!• Greater Newark's Hometown N :· . I. ·. Newark, Del. • 50¢ 86th Year, Issue 24 ©1996 Jur.· 28, 1996 THIS WEEK Bridge IN SPORTS "·-· over LOCALRNALS troubled UNITE FOR THE BLUE concrete GoLDALL Elkton Road could be closed STAR GAME. 19 for bridge repairs By MARY E. PETZAK ••t t ffOfOOOfOOowo o o o oo o o o oo• oo oo o toooo o ooooo o oao o ooO . IN LIFESTV:LE NEWARK POST STAFF WR ITER One of Newark 's most-tra ' leu thoroughfares could b ~ hut dow n for repairs in the neur future. Bors &GIRLS Ac cordin g to cit y manag r Carl Lufl. officials al th e . tale department of tran ponation advi sed the city" . CLUB, BAYARD DoNATION TO CHS liBRARY traffi c division last week th at th e Elk ton Road bridg over th e hri stina Mrs. Elmer s. Monroe, right, recently donated her collection of 300 National Geographic magazines reek nedr Casho Mill Road mi ght TFAM UP FOR dating back to the 1950s to the library at Christiana High School. Her late husband served as a huve to be clos d for repair.. member of the Christina School District Board of Education. Accepting the donation Is Sylvia "I don 't want to be an alarmi st " Williamson. of the school district staff. Mrs. Williamson graduated from Newark High School when UNUSUAL Mr. Monroe was on the school board. See BRIDGE , 2 ...,_ ACfiVITY. 8 - " · IN' THE NEWS. '• QSTIX SCRATCHES HlTE CLAY Creek make an appearance, and 60 Civil ttofAfilt;c•J-JJ State Park will be the War re.-enactots will be . -

A Celebration of Lifes Simple Pleasures Pdf, Epub, Ebook
JUST LITTLE THINGS: A CELEBRATION OF LIFES SIMPLE PLEASURES PDF, EPUB, EBOOK Nancy Vu | 1 pages | 11 Jul 2013 | Penguin Putnam Inc | 9780399162978 | English | United States Just Little Things: A Celebration of Lifes Simple Pleasures PDF Book David Hockney. Based on the popular website, this book will strike a chord in anyone who is open to celebrating the little moments of greatness all around us. Vintage Paperback Celebrity Magazines. Explanation of what you received vs what you expected to receive. Nov 10, PST. Find it and experience true bliss. Back to home page. New other. More filters. The whole world is an art gallery when you're mindful. We care as much about your item as you do which is why each item is carefully packaged to ensure a safe delivery. See all 10 - All listings for this product. Let each day be a Festival of Joy. It made me think of things that I had either not thought about in a while or said Yes, I do like those things too. If you request to cancel through eBay within 30 minutes of when your order is placed, we will do our best to cancel, however, it is not guaranteed. Sara says:. One night I was watching TV in bed when one of them came in to kiss me goodnight carrying the balloon. Contact Us with your Feedback! This amount is subject to change until you make payment. For additional information, see the Global Shipping Program terms and conditions - opens in a new window or tab See details. God gave us the gift of life; it is up to us to give ourselves the gift of living well. -

Applying Insights from Cultural Studies to Adult Education: What Seinfeld Says About the AERC
Kansas State University Libraries New Prairie Press Adult Education Research Conference 1999 Conference Proceedings (DeKalb, IL) Applying Insights from Cultural Studies to Adult Education: What Seinfeld Says About the AERC Nod Miller University of East London, UK Follow this and additional works at: https://newprairiepress.org/aerc Part of the Adult and Continuing Education Administration Commons This work is licensed under a Creative Commons Attribution-Noncommercial 4.0 License Recommended Citation Miller, Nod (1999). "Applying Insights from Cultural Studies to Adult Education: What Seinfeld Says About the AERC," Adult Education Research Conference. https://newprairiepress.org/aerc/1999/papers/30 This is brought to you for free and open access by the Conferences at New Prairie Press. It has been accepted for inclusion in Adult Education Research Conference by an authorized administrator of New Prairie Press. For more information, please contact [email protected]. Applying Insights from Cultural Studies to Adult Education: What Seinfeld Says About the AERC Nod Miller University of East London, UK Abstract: The zany adventures of a glamorous British professor who goes to an important international conference but spends most of her time searching for a TV in order to watch her favourite sitcom. Despite her commitment to "no hugging, no learning", she gains some profound insights into mass culture, adult education, friendship and postmodernity as a result. Parental guidance suggested. Prologue: The Convergence This paper has grown out of a critical incident in my own learning biography, where a convergence of two cultural events brought together several discrete elements of my personal and professional identity and led me to reflect on aspects of relationships between the mass media and adult education. -

DVD SPOTLIGHT BATMAN BEGINS PAGE 46 Plus
Cover_October 05 9/6/05 11:28 AM Page 1 3/C B G october 2005 | volume 6 | number 10 R DVD SPOTLIGHT BATMAN BEGINS PAGE 46 Plus... KEVIN 100 2 5 25 50 75 95 98 BACON on WHERE THE TRUTH LIES IN HER SHOES’ CAMERON DIAZ 100 2 5 25 50 75 95 98 ORLANDO BLOOMtalks ELIZABETHTOWN 100 2 5 25 50 75 95 98 100 2 5 25 50 75 95 98 PUBLICATIONS MAIL AGREEMENT NO. 40708019 ANTHONY HOPKINS, GWYNETH PALTROW AND OTHER STARS RECOMMEND READING Famous Proof 9/8/05 12:35 PM Page 1 3/C B The biggest risk in life G is not taking one. R 100 2 5 25 50 75 95 98 Gwyneth Paltrow Anthony Hopkins 100 2 5 25 50 75 95 98 Jake Gyllenhaal Hope Davis 100 2 5 25 50 75 95 98 Based on the Pulitzer Prize Winner ® From the Director of the Academy Award Winning Film “Shakespeare in Love” 100 2 5 25 50 75 95 98 MIRAMAX FILMS PRESENTS IN ASSOCIATION WITH ENDGAME ENTERTAINMENT A HART SHARP ENTERTAINMENT PRODUCTION A FILM BY JOHN MADDEN GWYNETH PALTROW ANTHONY HOPKINS JAKE GYLLENHAAL HOPE DAVIS “PROOF” CASTING MUSIC COSTUME EDITED PRODUCTION DIRECTOR OF CO-EXECUTIVE BYBILLY HOPKINS SUZANNE SMITH KERRY BARDENBY STEPHEN WARBECKDESIGNER JILL TAYLORBY MICK AUDSLEYDESIGNER ALICE NORMINGTONPHOTOGRAPHY ALWIN KÜCHLER, BSC CO-PRODUCERMARK COOPERPRODUCER MICHAEL HOGAN EXECUTIVE PRODUCED BASED ON SCREENPLAY DIRECTED PRODUCERSBOB WEINSTEIN HARVEY WEINSTEIN JULIE GOLDSTEIN JAMES D.STERNBY JEFFREY SHARP JOHN N.HART JR. ROBERT KESSEL ALISON OWENTHE PLAY BY DAVID AUBURNBY DAVID AUBURN AND REBECCA MILLERBY JOHN MADDEN SOUNDTRACK AVAILABLE ON www.proof-movie.com ARTWORK ©2005 MIRAMAX FILM CORP. -

The Culture of Post-Narcissism
THE CULTURE OF POST-NARCISSISM The Culture of Post-Narcissism Post-teenage, Pre-midlife Singles Culture in Seinfeld, Friends, and Ally – Seinfeld in Particular MICHAEL SKOVMAND In a recent article, David P. Pierson makes a persuasive case for considering American television comedy, and sitcoms in particular, as ‘Modern Comedies of Manners’. These comedies afford a particular point of entry into contemporary mediatised negotiations of ‘civility’, i.e. how individual desires and values interface with the conventions and stand- ards of families, peer groups and society at large. The apparent triviality of subject matter and the hermetic appearance of the groups depicted may deceive the unsuspecting me- dia researcher into believing that these comedies are indeed “shows about nothing”. The following is an attempt to point to a particular range of contemporary American televi- sion comedies as sites of ongoing negotiations of behavioural anxieties within post-teen- age, pre-midlife singles culture – a culture which in many aspects seems to articulate central concerns of society as a whole. This range of comedies can also be seen, in a variety of ways, to point to new ways in which contemporary television comedy articu- lates audience relations and relations to contemporary culture as a whole. American television series embody the time-honoured American continental dicho- tomy between the West Coast and the East Coast. The West Coast – LA – signifies the Barbie dolls of Baywatch, and the overgrown high school kids of Beverly Hills 90210. On the East Coast – more specifically New York and Boston, a sophisticated tradition of television comedy has developed since the early 1980s far removed from the beach boys and girls of California.