A Comparative Analysis Through Time and Space of Centrality’S Role in County Centers’ Spatial Position for Several Counties in Romania
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Proces-Verbal De Desemnare a Operatorilor De Calculator Ai
3URFHVYHUEDOGHGHVHPQDUHDRSHUDWRULORUGHFDOFXODWRUDLELURXULORUHOHFWRUDOHDOHVHFĠLLORU GHYRWDUHFRQVWLWXLWHSHQWUXDOHJHUHDDXWRULWă܊LORUDGPLQLVWUD܊LHLSXEOLFHORFDOHGLQGDWDGH27 septembrie 2020, conform deciziei AEP nr. 52 din 04.09.2020, %LURXO(OHFWRUDOGH&LUFXPVFULS܊LH-XGHĠHDQăQU21 HARGHITA Nr. crt. UAT 1U6HF܊LH ,QVWLWX܊LD Nume Prenume ,QL܊LDOD )XQF܊LD WDWăOXL 1 MUNICIPIUL 1 TEATRUL MUNICIPAL ´CSIKI CÂMPEAN LIVIU-MANOLE Operator MIERCUREA-CIUC JÁTÉKSZÍN´MIERCUREA-CIUC 2 MUNICIPIUL 2 LICEUL DE ARTE ´NAGY ISTVÁN´ MIHALCEA 0$5(܇9,25(/ Operator MIERCUREA-CIUC MIERCUREA-CIUC 3 MUNICIPIUL 3 &$6$'(&8/785Ă$6,1',&$7(/25 PAP MARIA A Operator MIERCUREA-CIUC MIERCUREA-CIUC 4 MUNICIPIUL 4 ܇&2$/$*,01$=,$/Ă´NAGY IMRE´ INCZE RÉKA Operator MIERCUREA-CIUC MIERCUREA-CIUC 5 MUNICIPIUL 5 ù&2$/$*,01$=,$/ĂÄNAGY IMRE´ GABOR LORÁND Operator MIERCUREA-CIUC MIERCUREA-CIUC 6 MUNICIPIUL 6 ܇FRDOD*LPQD]LDOă´Nagy Imre´ POPESCU CRISTINA Operator MIERCUREA-CIUC 7 MUNICIPIUL 7 ܇&2$/$*,01$=,$/Ă´3(7ė), SZÁSZ Zsófia A Operator MIERCUREA-CIUC SÁNDOR´MIERCUREA-CIUC 8 MUNICIPIUL 8 ܇&2$/$*,01$=,$/Ă´3(7ė), OZSVÁTH-BERÉNYI HAJNALKA-JUDIT Operator MIERCUREA-CIUC SÁNDOR´MIERCUREA-CIUC 9 MUNICIPIUL 9 ܇&2$/$*,01$=,$/Ă´LIVIU GYÖRGY Adél A Operator MIERCUREA-CIUC REBREANU´MIERCUREA-CIUC 10 MUNICIPIUL 10 *5Ă',1,ğ$ÄNAPRAFORGÓ´ GALEA MIHAI-VLAD Operator MIERCUREA-CIUC MIERCUREA-CIUC ^ƚƌ͘^ƚĂǀƌŽƉŽůĞŽƐ͕Ŷƌ͘ϲ͕ƵĐƵƌĞƔƚŝ͕^ĞĐƚŽƌϯ͕ϬϯϬϬϴϰ 1/23 Telefon: 021.310.07.69, fax: 021.310.13.86 www.roaep.ro, e-mail: [email protected] 3URFHVYHUEDOGHGHVHPQDUHDRSHUDWRULORUGHFDOFXODWRUDLELURXULORUHOHFWRUDOHDOHVHFĠLLORU -

Some Actual Aspects About the Tourism Accomodation in Harghita County
GeoJournal of Tourism and Geosites Year VII, no. 2, vol. 14, November 2014, p.158-167 ISSN 2065-0817, E-ISSN 2065-1198 Article no. 14106-162 SOME ACTUAL ASPECTS ABOUT THE TOURISM ACCOMODATION IN HARGHITA COUNTY George-Bogdan TOFAN* “Babeş-Bolyai” University, Faculty of Geography, Cluj-Napoca, 5-7 Clinicilor Street, 40006, Romania, e-mail: [email protected] Adrian NIŢĂ “Babeş-Bolyai” University, Faculty of Geography, Gheorgheni Branch, Romania, e-mail: [email protected] Abstract: The aim of the study is to synthetically present the tendencies of one of the most important elements of the tourism, the accommodation, within Harghita County. Analyzed for more than two decades, quantitatively it presents an evolution with different positive and negative rates. By categories, the tourist villas dominate at the beginning of the ’90s, especially in the tourist resorts of the county (Borsec, Lacu Roşu, Izvoru Mureşului, Harghita-Băi, Băile Tuşnad, Băile Homorod). Later the situation changed for newer categories, existing and functioning on private initiatives (tourist pensions, agritourist pensions, bungalows), plus for some of the classic categories, the tourist chalet, adapted for the mountain tourism, the hotel, present especially in urban settlements and several resorts (Miercurea-Ciuc, Gheorgheni, Odorheiu Secuiesc, Topliţa, Băile Tuşnad, Harghita-Băi, Borsec), the motel and the tourist stop, specific to the automobile travel. Key words: accommodation, comfort degree, villas, tourist pensions, Harghita * * * * * * INTRODUCTION Aspects about the evolution of the accommodation in Harghita County were presented before in several studies approaching the geographic domain at national level (Geografia României, Geografia Umană şi Economică, 1984), at county level (the Romanian Academy series about the Romanian Counties, Judeţul Harghita, Pişotă, Iancu, Bugă, 1976; Judeţul Harghita, Cocean et al., 2013) or in some doctoral theses regarding the mountain depressions (Şeer, 2004, Mara, 2008, Tofan, 2013). -

Draft Map and the List of Administrative Units
Defining the Scope of Application for the Strategy for Development of Sustainable Tourism of the Carpathians: Draft map and the list of administrative units The Carpathian Convention Working Group on Sustainable Tourism at its meeting on 12-14 May 2014, Bratislava, Slovakia, discussed the map presented below. The Working Group concluded that along with administrative units, the map should include the geographical scope of the Carpathians as it is currently defined by the Party. The geographical scope of the Carpathians defines the core area for implementing the actions outlined in the strategy, while the administrative borders are useful for decision making, resource allocation and monitoring purposes. The Working Group decided to develop two maps that may be useful during the implementation of the strategy: 1. A map of local administrative units on LAU1 level in EU countries, “raions” in Ukraine and municipalities in Serbia that also features the geographical scope of the Carpathians. Such map may be helpful when involving the authorities and stakeholders into project development and implementation and when action is needed for decision making and implementation on the smallest administrative level. 2. A map of administrative units at NUTS3 or NUTS2 level, “oblast” in Ukraine and districts in Serbia that also features the geographical scope of the Carpathians. Such map would be useful when action is needed on the regional decision level, and whenever the interlinkage of the Carpathians with surrounding areas is important (e.g. for optimizing -
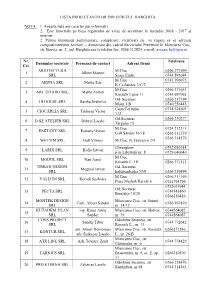
Evidenta-Proiectanti-Final
LISTA PROIECTANTILOR DIN JUDETUL HARGHITA NOTA: 1. Această lista are caracter pur informativ 2. Este întocmită pe baza registrului de avize de securitate la incendiu 2008 - 2017 şi internet. 2. Pentru informaţii suplimentare, completare, rectificări etc. vă rugam să vă adresați compartimentului Avizare – Autorizare din cadrul Serviciului Prevenire în Miercurea Ciuc, str. Borviz, nr. 2, jud. Harghita sau la telefon/fax: 0266 312824, e-mail: [email protected] Nr. Telefoane Denumire societate Persoană de contact Adresă firmă Crt. ARHITECTURA M.Ciuc 0266 371690 1 Albert Marton SRL Szasz Endre 0744 593694 M.Ciuc 0745 396075 2 AEDNA SRL Mathe Ede K.Cs.Sandor 3/C/2 M.Ciuc 0266 371651 3 ARC STUDIO SRL Mathe Zoltan Kossuth Lajos 11 0744 697961 Od. Secuiesc 0266 217199 4 1B HOUSE SRL Bartha Szabolcs Morii 1/B 0740 256445 Capu Corbului 0728 524601 5 CIOCÂRLIA SRL Tudoran Victor 112 Od.Secuiesc 0266 210277 6 D-SZ ATELIER SRL Dobrai Laszlo Târgului 15 M.Ciuc 0724 212311 7 ESZTANY SRL Esztany Gyozo Gall Sandor 16/18 0266 311539 0266 314576 8 WELTIM SRL Gall Vilmos M.Ciuc, N. Balcescu 2/4 Gheorgheni 0742 010144 9 LARIX SRL Kollo Istvan p-ţa Libertăţii nr. 8 0729 040040 M.Ciuc 10 MODUL SRL Nan Aurel Kossuth L. 18 0266 371511 URBAN DESIGN Od. Secuiesc 11 Magyari Istvan SRL Independenţei 53/8 0266 219499 M.Ciuc 0266 311169 12 VALLUM SRL Korodi Szabolcs Piaţa Majlath Karoly 6 0744793799 0732633944 Od. Secuiesc 13 PECTA SRL 0744345460 Breslelor 16/20 0266216426 MONTEK DESIGN Miercurea Ciuc, str. Inimii, 14 Carh. -

Studiu De Piaţă Judeţul Harghita
CAMERA NOTARILOR PUBLICI TÂRGU MUREŞ Târgu Mureş, str. Căprioarei, nr. 7., jud. Mureş Telefon +40 265 250 050 Fax 0372 255 097 e-mail: [email protected] STUDIU DE PIAŢĂ JUDEŢUL HARGHITA -ANUL 2020- EXPERŢILOR TEHNICI MUREŞ S.R.L. Târgu Mureş, str. Arany János, nr. 18., jud. Mureş Telefon +40 265 214 169 Fax +40 265 250 021 e-mail: [email protected] Studiu de piaţă privind valorile minime consemnate pe piaţa imobiliară - Judeţul Harghita CUPRINS Introducere 6 Capitolul 1. Prezentarea datelor 9 Apartamente situate în clădiri - blocuri de locuințe - 12 condominiu – cu destinație rezidențială Clădiri de locuit individuale (familiale) şi anexele acestora 15 Clădiri-construcţii nerezidenţiale 21 Terenuri situate în intravilanul localităţilor 30 Terenuri situate în extravilanul localităţilor 34 Capitolul 2. Tabele privind valorile minime 42 Judeţul Harghita, Circumscripţia Notarială Miercurea Ciuc 43 o Apartamente din clădiri - blocuri de locuințe - condominiu – cu 44 destinație rezidențială o Apartamente cu suprafaţă utilă ≤ 40 mp 44 o Apartamente cu suprafaţă utilă > 40 şi ≤ 70 mp 45 o Apartamente cu suprafaţă utilă >70 mp 46 o Anexe ale apartamentelor 47 o Clădiri de locuit individuale (familiale) şi anexele acestora 48 o Anexe gospodăreşti la clădirile de locuit individuale (familiale) 50 o Clădiri - costrucţii cu detinație nerezidenţială 54 o Costrucţii administrative și social-culturale 54 o Construcţii industriale și edilitare 57 o Costrucţii anexă 59 o Terenuri situate în intravilanul localităţilor 62 o Terenuri situate -

Circumscripţia Electorala Sediul Biroului Electoral De Circumscripţie
SEDIUL ŞI DATELE DE CONTACT ALE BIROULUI ELECTORAL DE CIRCUMSCRIPŢIE JUDEŢEANĂ NR. 21 HARGHITA SI ALE BIROURILOR ELECTORALE MUNICIPALE, ORAŞENEŞTI, COMUNALE ALEGERILE LOCALE 27 SEPTEMBRIE 2020 Circumscripţia Sediul Datele de contact Program de electorala Biroului electoral activitate de circumscripţie Adresa poştală Telefon Fax E-mail locală CIRCUMSCRIPŢIA PALATUL MUNICIPIUL 0266320020 0266320022 [email protected] Zilnic între orele ELECTORALĂ ADMINISTRATIV MIERCUREA CIUC 09.00 – 17.00 * JUDEŢEANĂ CAMERA 13 P-ŢA LIBERTAŢII NR. HARGHITA 5, PARTER, CAMERA 13 COD 530100 JUD.HARGHITA CIRCUMSCRIPŢIA SEDIUL MUNICIPIUL 0266315120/ 0266371165 [email protected] Zilnic între orele ELECTORALĂ PRIMĂRIEI MUN. MIERCUREA-CIUC, 104 [email protected] 09.00 – 17.00 * MUNICIPALĂ MIERCUREA- PŢA. CETĂŢII NR. 1, MIERCUREA- CIUC CIUC,ET. 1, COD 530110 CAMERA NR. 119, JUD. HARGHITA SALA DE ȘEDINȚE CIRCUMSCRIPŢIA CLĂDIREA UATM MUNICIPIUL 0266364006 0266364006 [email protected] Zilnic între orele ELECTORALĂ GHEORGHENI, GHEORGHENI, STR. 0784258447 [email protected] 09.00 – 17.00 * MUNICIPALĂ unde are sediul CARPAŢI NR. 1, GHEORGHENI Compartimentul COD 535500 protecția civilă, JUD. HARGHITA sănătate și securitate în muncă al UATM Gheorgheni CIRCUMSCRIPŢIA PRIMARIA MUNICIPIUL 0266218145 0266218032 hr.odorheiusecuiesc@be Zilnic între orele ELECTORALĂ MUNICIPIULUI ODORHEIU c.ro 09.00 – 17.00 * MUNICIPALĂ ODORHEIU SECUIESC, PIAȚA [email protected] ODORHEIU SECUIESC, VÁROSHÁZA NR. 5 SECUIESC CLĂDIRE COD: 535600 PRIMĂRIEI, JUD. HARGHITA ETAJUL II, CAMERA -

RAPORT Februarie 2020
COMISIA DE DIALOG SOCIAL de la nivelul Judeţului Harghita Raport privind activitatea Comisiei de Dialog Social pe luna februarie 2020 Nr. Data Ordinea de zi crt. şedinţei Punct propus Iniţiator Rezultatul concluziilor sau al eventualelor comisiei de rezoluţii dialog social 1. Temă de interes local: - Din răspunsurile date de către primării, ca urmare a Situaţia cabinetelor medicale Directorul executiv al unei adrese transmise de către reprezentanţii DSP 1. 25.02.2020 şcolare din judeţul Harghita Direcţiei de Sănătate Harghita au rezultat următoarele concluzii: (cadrul legal actual de Publică Harghita - 7 primării au încheiat deja un contract de funcţionare al activităţilor prin colaborare cu medicul de familie pentru care este asigurată asistenţa servicii de asistenţă medicală acordate medicală; gradul de acoperire cu preşcolarilor, şcolarilor din unităţile de servicii medicale la unităţile învăţământ: Căpâlnița, Ciceu, Ocland, Satu şcolare din judeţ; funcţionarea Mare, Sândominic și Sânmartin; sistemului în momentul de faţă, - 3 primării au informat că medicul de familie a precum şi alte aspecte asigurat şi asigură asistenţa medicală în şcoli considerate a fi de interes). şi fără contract de colaborare: Plăieșii de Jos, Mihăileni (cu asistent medical comunitar), iar Sântimbru (are intenţia de a înfiinţa cabinet); - 3 primării au informat că triajul epidemiologic şi examenele de bilanţ sunt realizate de asistentul medical comunitar în colaborare şi sub îndrumarea, coordonarea medicului/medicilor de familie: Borsec, Mihăileni și Vlăhița. -

RAPORT VACCINARE.Pdf 528,1 KO
D I R E C Ţ I A D E S Ă N Ă T A T E P U B L I C Ă H A R G H I T A 530180, Miercurea-Ciuc, Str.Mikó nr. 1 tel: 0266-310423, fax: 0266-371142 e-mail: [email protected]; http://www.dspharghita.ro Nr. 1125/19.02.2021 Către, INSTITUȚIA PREFECTULUI JUDEȚUL HARGHITA Raport vaccinări COVID-19 în județul Harghita Vaccinarea împotriva COVID-19 în România se realizeză în trei etape, în care vor fi vaccinate grupele populaționale eligibile pentru etapa respectivă. Recomandările privind grupurile prioritare au fost elaborate în concordanţă cu documente emise de OMS şi ECDC în urma consultărilor de ţară realizate cu 19 ţări din Europa şi a analizei situaţiei existente în România. Recomandările STRATEGIEI DE VACCINARE ÎMPOTRIVA COVID 19 ÎN ROMÂNIA sunt în dinamică şi pot fi actualizate în funcţie de evoluţia pandemiei de COVID-19 şi de eficienţa tipurilor de vaccinuri aprobate şi disponibile pentru diferite categorii populaţionale. Aceste grupuri prioritare sunt cele care ar trebui vaccinate în prima etapă, urmând ca, odată epuizată această etapă, vaccinarea să fie disponibilă pentru toată populaţia, în vederea asigurării protecţiei faţă de formele severe şi realizării imunităţii colective, estimată în prezent la circa 70% din totalul populaţiei. (STRATEGIE din 27 noiembrie 2020 de vaccinare împotriva COVID-19 în România - MONITORUL OFICIAL nr. 1171 din 3 decembrie 2020, actualizat) Conform strategiei pentru vaccinarea împotriva COVID-19 în România vaccinarea este voluntară, ne-obligatorie și gratuită. Documentul are în vedere întregul proces și lanț de vaccinare împotriva COVID 19, de la principiile generale, până la organizarea vaccinării, depozitarea vaccinurilor, păstrarea lanțului de frig, monitorizarea siguranței și eficacității și managementul deșeurilor. -

Lista Fondurilor Şi Colecţiilor Date În Cercetare De Către Direcţia Judeţeană Harghita a Arhivelor Naţionale
Lista fondurilor şi colecţiilor date în cercetare de către Direcţia Judeţeană Harghita a Arhivelor Naţionale Nr. inventar Denumirea fondului sau colecţiei Anii extremi Nr. u.a. Nr. crt. 1. 23; 24; 243 Administraţia de Domenii Márpatak din Tulgheş. 1841 - 1864 899 2. 341 Administraţia Finanaciară a judeţului Odorhei. 1928 - 1949 171 3. 342; 344-348; Administraţia Financiară a judeţului Ciuc. 1915 - 1956 170 996; 997 4. 404 Asociaţia de Educaţie Populară Odorhei. 1869 - 1926 13 5. 323 Asociaţia Joagărelor de pe Olt din Băile Tuşnad. 1915 - 1949 1 6. 862 Asociaţia Română pentru legători cu U.R.S.S. (A.R.L.U.S.) – 1946 - 1959 27 Judeţeană şi Raională Ciuc. 7. 863 Asociaţia Română pentru legători cu U.R.S.S. (A.R.L.U.S.) – 1947 - 1957 9 Judeţeană şi Raională Odorhei. 8. 946 Asociaţii şi Organizaţii Obsteşti. 1910 - 1967 58 9. 224 Atelier de Reparat Maşini Fraţii Bartox din Odorhei. 1921 - 1950 21 10. 406 Avocatura Statului din judeţul Ciuc. 1921 - 1940 7 11. 743 Banca Agricolă Sucursala Regională Mureş – Topliţa. 1955 - 1960 29 12. 709 Banca de Investiţii Miercurea Ciuc. 1950 - 1966 379 13. 324 Banca Naţională a României – Sucursala Miercurea Ciuc. 1944 - 1951 136 13. 687 Şcoala de instructori superiori de pionieri Cristur. 1952 - 1954 13 14. 320 Banca Naţională a României – Sucursala Odorhei. 1930 - 1950 45 15. 703 Banca Naţională a României – Sucursala Topliţa. 1948 - 1968 65 16. 1013 Banca Populară “Speranţa” Joseni. 1924 - 1947 71 17. 8 Banca Populară Gheorgheni. 1947 - 1948 7 18. 187 Banca Populară Lăzarea. 1929 - 1947 2 19. 315 Biroul Electoral Judeţean Ciuc. -

Raport Corel 15 Final Tipar.Cdr
Building foundations 2012 for stronger communities Community foundations contribute to the for the future community foundations in transformation of local communities, so Oradea, Prahova, Bacău and Țara they can reach their development Făgărașului were also launched. potential, based on the opportunities, the resources and the ideals of their Two regional funds are also established inhabitants. They help build dynamic, based on local leadership: in Cristuru connected and supportive communities, Secuiesc, hosted by Odorheiu Secuiesc with a higher living standard. Community Foundations and in Reghin, hosted by Mureș Community Foundation. Community foundations are local organizations; they support philanthropy, The Romanian Community Foundations encourage the community spirit and offer Federation was created in 2012, as a financial support to projects from various representation platform for community areas – education, culture, environment foundation, supporting the development protection, and youth development. of philanthropy at a national level. Community foundations build funds, This report presents the framework, starting from the philanthropic interests of participants and results of a national donors, which they channel back towards support program to help develop communities as grants and scholarships. At community foundations in Romania. The the same time, they also support non- program was initiated by Association of profit organizations, initiative groups and Community Relations (ARC) and had two individuals and take leadership in building main stages so far: 2006-2008 and 2009- dialogue and cooperation platforms to 2012. address community needs or opportunities. The current stage of the program has been implemented in cooperation with The first community foundations were Romanian Environmental Partnership established in Romania five years ago in Foundation and PACT Foundation and is Cluj and Odorheiu Secuiesc. -

Plan Urbanistic Zonal Proiect Regional De Dezvoltare Infrastructurii De Apă Și Apă Uzată În Județul Harghita
s.c. ARHITECTURA s.r.l. MIERCUREA CIUC, str. ZÖLD PÉTER nr 19, jud. HARGHITA tel. 0744 593 694 PLAN URBANISTIC ZONAL PROIECT REGIONAL DE DEZVOLTARE INFRASTRUCTURII DE APĂ ȘI APĂ UZATĂ ÎN JUDEȚUL HARGHITA BENEFICIAR: S.C. HARVIZ SA PROIECTAT: S.C. ARHITECTURA S.R.L. PROIECT NR. 1602/2020 s.c. ARHITECTURA s.r.l. MIERCUREA CIUC, str. ZÖLD PÉTER nr 19, jud. HARGHITA tel. 0744 593 694 Denumirea lucrării Proiect regional de dezvoltare infrastructurii de apă și apă uzată în județul Harghita Amplasament com. SÂNSIMION, sat CETĂȚUIA com. ZETEA, sat SUB CETATE, sat IZVOARE com. SÂNCRĂIENI, sat SÂNCRĂIENI mun. ODORHEIU SECUIESC mun. MIERCUREA CIUC, zona CIBA, zona SZÉCSENY com. CIUCSÂNGEORGIU, sat COTORMANI com. PLĂIEȘII DE JOS, sat PLĂIEȘII DE JOS, sat CAȘINU NOU com. PRAID, sat BUCIN Inițiator S.C. HARVIZ SA Beneficiar S.C. HARVIZ SA Proiectant general S.C. ARHITECTURA S.R.L. Miercurea Ciuc, str. Zöld Péter nr. 19 Faza P.U.Z. Număr contract 1602/2020 Volumul Piese scrise și desenate – Plan urbanistic zonal (PUZ) Prevederi generale Director S.C. ARHITECTURA S.R.L. arh. ALBERT MARTIN Miercurea Ciuc, 07.07. 2020 s.c. ARHITECTURA s.r.l. MIERCUREA CIUC, str. ZÖLD PÉTER nr 19, jud. HARGHITA tel. 0744 593 694 COLECTIV TEHNIC DE COORDONARE GENERALĂ A PROIECTULUI S.C. ARHITECTURA S.R.L. arh. ALBERT MARTIN atestat R.U.R. PROIECTANȚI P.U.Z. ȘEF PROIECT dipl. arh. ALBERT MARTIN ARHITECTURĂ dipl. arh. ALBERT MARTIN dipl. arh. ALBERT MARIANA dipl. arh. BÍRÓ JÓZSEF dipl. arh. LÁSZLÓ BEÁTA Miercurea Ciuc, 07.07.2020 s.c. -

C U P R I N S
ROMÂNIA Nesecret MINISTERUL AFACERILOR INTERNE Instituţia prefectului – Judeţul Harghita Nr. 9415 Data: 03.06.2019 R A P O R T U L A N U A L privind starea economico - socială a judeţului Harghita, pe anul 2018 C U P R I N S PREZENTAREA GENERALĂ A JUDEŢULUI HARGHITA ............................... 1 1. STAREA ECONOMICĂ ............................................................................ 6 1.1. Evoluţia principalelor sectoare economice .................................................... 6 a). Industrie .................................................................................................... 6 b). Agricultura ............................................................................................... 19 c). Turism ..................................................................................................... 29 1.2. Amenajarea teritoriului, urbanism şi locuinţe, servicii publice de gospodărie comunală ................................................................................ 36 a). Urbanism şi amenajarea teritoriului ............................................................ 36 b). Locuinţe ................................................................................................... 38 c). Servicii comunitare de utilităţi publice ......................................................... 39 1.3. Stadiul realizării programului de investiţii ................................................... 73 1.4. Comerţ şi protecţia consumatorului ........................................................... 82