Minimum Lap Time of Race Cars: Modelling and Simulation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2 0 1 8 Motorsportbrochure
LIKE | facebook.com/TwynhamsTours VISIT | twynhamstours.co.uk 2018 MOTORSPORT BROCHURE FORMULA ONE / MILLE MIGLIA / MONACO HISTORIC GP TWYNHAMS TOURS | INTRODUCTION 1 GOODWOOD REVIVAL / SILVERSTONE CLASSIC / SPA SIX HOURS LIKE | facebook.com/TwynhamsTours VISIT | twynhamstours.co.uk It’s impossible to keep this brochure updated throughout the season. So for up-to-minute information JOIN US FOR A TRULY GREAT ONLINE you can keep in touch online. LINE UP OF MOTORSPORT TOURS IN 2018 Following on from our hugely popular 2017 Classic motorsport events are well catered for motorsport season, we are pleased to present with the Mille Miglia Hosted Tour, the Twynhams our new and expanded 2018 motorsport tours Tours’ exclusive Brooklands Hospitality Suite brochure. for the Silverstone Classic, the Belmond British Pullman trip to the amazing period spectacle that We continue to innovate and expand our event is the Goodwood Revival. And new for this year portfolio in conjunction with the rich heritage of we present the Spa Six Hours race in September. core motorsport events that you request year- on-year. 2017 saw the launch of our enormously successful Aviation Tours business. For 2018 we are adding WEB FACEBOOK TWITTER Our unwavering desire to create perfect events an incredible line up of new tours, passenger for the enthusiast has led us to concentrate our flight packages and airshow hospitality. These efforts on creating ‘hosted tours’, whether that are all showcased in our comprehensive new Book your VIP Tours securely online 24 hours a day in We have one of the UK’s most popular hospitality Our Twitter feed delivers the freshest, most relevant be to the Mille Miglia or Italian Grand Prix. -

Race Preview 2013 ITALIAN GRAND PRIX 06 – 08 SEPTEMBER 2013
Race Preview 2013 ITALIAN GRAND PRIX 06 – 08 SEPTEMBER 2013 Round 12 of the 2013 Formula One World CIRCUIT DATA Championship marks the sport’s final race of the AUTODROMO DI MONZA season in Europe and, as has become traditional, Length of lap: 5.793km it takes place at one of F1’s great venues – Italy’s Lap record: 1:21.046 Monza circuit. (Rubens Barrichello, Ferrari, 2004) F1’s original temple of speed, La Pista Magica, as it is Start/finish line offset: known, is now out on its own in modern F1 as a true 0.309km low-downforce, high-speed circuit, with just a handful Total number of race laps: 53 of fast bends and chicanes to get in the way of drivers Total race distance: 306.720km clocking the highest average lap speed of any track on Pitlane speed limits: the current calendar – around 245kmh. 80km/h throughout the entire event weekend. The presence of slow chicanes breaking the high- speed straights means that suspension settings are CHANGES TO THE crucial, as to secure a good lap time drivers need CIRCUIT SINCE 2012 to be able to ride the kerbs hard. The flat out nature ►The leading edges of the of the track also means that engines take more kerbs at the apex of Turn 1 punishment than at most circuits with up to 70 per and 4 will be longer, to avoid the possibility of a car being cent of a lap being run at full throttle. The final effect launched when crossing them. of all that speed is that tyres are subjected to heavy ►The kerb at the exit of Turn longitudinal forces under braking and blistering can be 6 will be extended by 20m in an issue. -
Tony Stewart
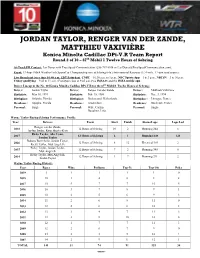
JORDAN TAYLOR, RENGER VAN DER ZANDE, MATTHIEU VAXIVIÈRE Konica Minolta Cadillac DPi-V.R Team Report Round 2 of 10 – 67th Mobil 1 Twelve Hours of Sebring At-Track PR Contact: Laz Denes with True Speed Communication (256-717-8014 or [email protected]). Event: 12-hour IMSA WeatherTech SportsCar Championship race at Sebring (Fla.) International Raceway (3.74-mile, 17-turn road course). Live Broadcast (race time 10:40 a.m. EDT Saturday): CNBC – 10:30 a.m. to 1 p.m.; NBC Sports App – 1 to 3 p.m.; NBCSN – 3 to 10 p.m. Friday qualifying – 9:45 to 11 a.m. (Prototype class at 9:45 a.m.) via IMSA.tv and the IMSA mobile app. Driver Lineup in the No. 10 Konica Minolta Cadillac DPi-V.R for the 67th Mobil 1 Twelve Hours of Sebring: Driver: Jordan Taylor Driver: Renger van der Zande Driver: Matthieu Vaxivière Birthdate: May 10, 1991 Birthdate: Feb. 16, 1986 Birthdate: Dec. 3, 1994 Birthplace: Orlando, Florida Birthplace: Dodewaard, Netherlands Birthplace: Limoges, France Residence: Apopka, Florida Residence: Amsterdam Residence: Bordeaux, France Personal: Single Personal: Wife, Carlijn Personal: Single Daughter, Lola Wayne Taylor Racing Sebring Performance Profile: Year Drivers Event Start Finish Status/Laps Laps Led Renger van der Zande, 2018 12 Hours of Sebring 10 2 Running/344 8 Jordan Taylor, Ryan Hunter-Reay Ricky Taylor, Alex Lynn, 2017 12 Hours of Sebring 6 1 Running/348 123 Jordan Taylor Rubens Barrichello, Jordan Taylor, 2016 12 Hours of Sebring 8 12 Electrical/169 2 Ricky Taylor, Max Angelelli Ricky Taylor, Jordan Taylor, -

ACES WILD ACES WILD the Story of the British Grand Prix the STORY of the Peter Miller
ACES WILD ACES WILD The Story of the British Grand Prix THE STORY OF THE Peter Miller Motor racing is one of the most 10. 3. BRITISH GRAND PRIX exacting and dangerous sports in the world today. And Grand Prix racing for Formula 1 single-seater cars is the RIX GREATS toughest of them all. The ultimate ambition of every racing driver since 1950, when the com petition was first introduced, has been to be crowned as 'World Cham pion'. In this, his fourth book, author Peter Miller looks into the back ground of just one of the annual qualifying rounds-the British Grand Prix-which go to make up the elusive title. Although by no means the oldest motor race on the English sporting calendar, the British Grand Prix has become recognised as an epic and invariably dramatic event, since its inception at Silverstone, Northants, on October 2nd, 1948. Since gaining World Championship status in May, 1950 — it was in fact the very first event in the Drivers' Championships of the W orld-this race has captured the interest not only of racing enthusiasts, LOONS but also of the man in the street. It has been said that the supreme test of the courage, skill and virtuosity of a Grand Prix driver is to w in the Monaco Grand Prix through the narrow streets of Monte Carlo and the German Grand Prix at the notorious Nürburgring. Both of these gruelling circuits cer tainly stretch a driver's reflexes to the limit and the winner of these classic events is assured of his rightful place in racing history. -

Formula One Events Motorsport Travel, Race
.5 =82 /$3 + <- +< 38'-+3 + 82- + 2- - 954 7#0,, > 9@. / )-3 <'8% 2? "@ >23 -+ <%> )2( +:)8 %-8&3%-8 -+ 3 % 3/))3 -:8 ;'3'-+ *'$%8 %; + .13 :2$23 3+(3 + !-2 -2*:) .13 !:8:2 $2838 ;2 2';2 2))>'+$ <'8% %'3 .5 =82 /$3 + <- +< 38'-+3 + 82- + 2- .4% - 954 7# ,, > 9@. 0 / )-3 <'8% 2? "@ >23 -+ <%> )2( +:)8 %-8&3%-8 -+ 3 % 3/))3 -:8 ;'3'-+ *'$%8 %; + .13 :2$23 3+(3 + . 0 !-2 -2*:) .13 !:8:2 $2838 ;2 2';2 2 )>'+$ <'8% %'3 % . # D 9 /- >' & & >> + A ,)+>/- >' 91/8>79 >B/ 2&+)>> 8)-&3 18)E #/@8(>), ',19 981 #/8 #)A >@--)-& ),& 9 ' 78 )- >' 199 -& 8 9 > B' - #8/, @9>8+) B)9 + >9 ')9 ')8 /B- 6 /8 >' $89> >), )- 0 ')9>/8D >B/ #/@8(>), B/8+ ',1)/-9 &/ ' (>/(' #/8 $#>' >)>+ 4 C1 8> /1)-)/- - B)>' />' B)9 ,)+>/- - >> + )- @8 > ' -+D9)9 /# 8 9 /,1 >)>)A 89 >' $&'> #/8 9@18 ,D 9'/@+ >'8)++ 84 >79 /- - )>' 8 - ##/8 >/ +/9 " - -+D9)9 $ 888) - @++ '- 9 )- ?F0! * % .4% * ' > 8 )-9/879 # - 8 D/@8 &8)++)-& 8+/9 )-E 8) # ')9>/8D /# 8 A +9 ')9 #A/@8)> @8& 8 /8,@+ 0 # #' 9)> /B- B)>' >' 18 9) -> '# - C1+/8 ')9 A)9)/- #/8 0 > D,/-9 /- >' +> 9> /) 2$/ #$1 $/, * !#)2 ' /, $1 $/, )++ /8/ /99/ - /- * &**$# $) &$) # /))* ,$",$*( "( *$0) !! ,* # "$) * )!$* #3 * #,))$,$# @8-)-& )99@ /)+ 918)-&/8 >/ >> 8 >')-&9 6 :KHUH DUH DOO WKHVH SHRSOH FRPLQJ IURP" 5HQDXOW V KRVS WDOLW\ ,$ ) . )$ 7KDW V D JRRG TXHVWLRQ 0\ KDV EHHQ ÀDWRXW WKURXJK OXQFKWLPH DQG DV RQH RI WKH FUHZ JX GHV $ /, %) IDYRXU WH EXUJHU LV Q /RQGRQ ) 5DFLQJ WR RXU DSSRLQWHG WDEOH KHU IDFH FRQWRUWV LQWR D ULFWXV RI %) $ % % EXW , FDQ QHYHU FKRRVH EHWZHHQ GLVDSSURYDO DV VKH FORFNV WKH VWDLQV OHIW RQ WKH WDEOHFORWK E\ SUHYLRXV ) -) .)$ +RQHVW %XUJHUV DQG 3DWW\ %XQ JXHVWV (YLGHQFH RI WKH U RɣHQGLQJ VSODWWHU LV SURPSWO\ ZK VNHG DZD\ ) . -

July 2021 Contents Nick’S Natter Editorial 2021 Events It’S an Uphill Struggle Backfire Bits 2021 Calendar
Bristol Pegasus Motor Club Magazine Ace Classic Tour Photo Andy Moss July 2021 Contents Nick’s Natter Editorial 2021 Events It’s an uphill struggle Backfire Bits 2021 Calendar Motorsport UK RS Clubman licence Renew or Apply for your free 2021 Licence now ! From 2020 Motorsport UK introduced a requirement for all competitors to hold a new RS Clubman licence as a minimum, which is free of charge. If you compete, but don’t currently hold a licence you will need to apply for this. These changes will affect Autotests,Trials, Cross Country, Road Rallying, 12 Cars and Scatters. Passengers will also now be required to hold an RS Clubman licence. The RS Clubman licence can be applied for online and aims to encourage more grass roots participation, as well ensuring all Motorsport UK event competitors are covered by comprehensive insurance. Additionally, licence holders will have access to Motorsport UK’s Member Benefits Programme that includes the new upgraded personal accident cover. Online Application for the FREE RS Clubman licence begins here:- https://rsclubman.motorsportuk.org/ Nick's Natter Well the Cross Trophy Trial was good fun even if I didn’t do that well! Starting from July 25th and running until October we have now had confirmation that our monthly Breakfast meet will take place at Dean Forest Railway. Steam meets petrol. Breakfast baguettes will be available but if possible we would like a rough idea of numbers. I’ve just had a lovely scorching hot day at Thruxton. Andy & I went up in the Mustang which has excellent air con so we were nice and cool when we arrived. -

Carrera Cup Great Britain 2018
Carrera Cup Great Britain 2018 With the FIA Formula E Championship conrmed for 2019, an enhanced GT programme and other motorsport-related activities being evaluated, the future of Porsche Motorsport has never looked more exciting. Changes made to the Porsche Carrera Cup Great Britain 2018 championship are just as thrilling. The combination of an all-new 911 GT3 Cup, a new race format and a new points structure promises even more challenging racing for the drivers and teams and even more spectacle for the fans. The recent increased rewards and benets remain in place meaning Porsche Carrera Cup GB still oers unprecedented prize money in addition to extensive support and huge exposure. We are already looking forward to the exhilaration of Porsche Carrera Cup GB 2018 and hope you will join us for what promises to be the most action-packed championship yet. We wish you every success for 2018. Ragnar Schulte General Manager, Marketing Porsche Cars Great Britain All information and oers within this document are provisional and subject to MSA approval, and subject to contract and may be withdrawn by Porsche at any time. 4 Why Porsche? 6 Porsche Carrera Cup GB 8 2018 highlights 10 The new fastest one-make car in the UK 12 The new 911 GT3 Cup 14 New race format for the Pro category 15 New points structure 16 World-class 2018 race calendar 18 2018 championship dates 20 Rookie Championship 22 Porsche Carrera Cup GB Junior 2018/2019 24 Incredible prize money 26 Exceptional championship prizes 28 Registration fees 29 Early registration rewards 30 First-class driver well-being 32 Extensive team support 34 Team Cayenne 2018 36 Race weekend hospitality 38 Nationwide exposure and awareness 40 Media awareness 42 Sponsorship that works 44 Best of Porsche Carrera Cup GB 2017 4 Why Porsche? Porsche and motorsport: the two are inseparable With over 60 years of racing history and more than 32,000 victories to date, Porsche is the biggest manufacturer in the world to specialise in high performance cars and the most successful marque in motorsport. -
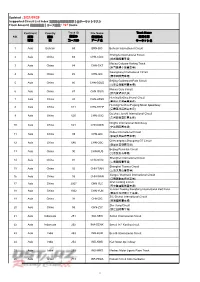
Updated : 2021/09/29 Supported Circuit List Index 支援的全球賽道清單│全サーキットリスト Track Amount 賽道總數量│コース総数 : 747 Tracks
Updated : 2021/09/29 Supported Circuit List Index 支援的全球賽道清單│全サーキットリスト Track Amount 賽道總數量│コース総数 : 747 tracks Continent Country Track ID File Name Track Name NO. 洲別 國家 賽道ID 賽道檔名 賽道名稱 地域 国 コースID データ名 サーキット名 1 Asia Bahrain 69 BRN-BIC Bahrain International Circuit Chengdu International Circuit 2 Asia China 83 CHN-CDIC (成都國際賽車場) Macau Coloane Karting Track 3 Asia China 84 CHN-CKT (澳門路環小型賽車場) Guangdong International Circuit 4 Asia China 85 CHN-GIC (廣東國際賽車場) Beijing Goldenport Park Circuit 5 Asia China 86 CHN-GOLD (北京金港國際賽車場) Macau Guia Circuit 6 Asia China 87 CHN-GUIA (澳門東望洋賽道) Hunting Beijing Shunyi Circuit 7 Asia China 88 CHN-HTBS (豪庭北京順義賽車場) Hunting Huizhou Fugang Motor Speedway 8 Asia China 611 CHN-HTHF (豪霆惠州福岗赛车场) Guizhou Junchi International Circuit 9 Asia China 620 CHN-JCIC (贵州骏驰国际赛车场) Ningbo International Speedway 10 Asia China 621 CHN-NBIS (宁波国际赛车场) Ordos International Circuit 11 Asia China 89 CHN-OIC (鄂爾多斯國際賽車場) Qinhuangdao Shougang GT Circuit 12 Asia China 640 CHN-QSC (秦皇岛首钢赛车场) Beijing Ruisiclub Circuit 13 Asia China 90 CHN-RUS (北京銳思賽車場) Shanghai International Circuit 14 Asia China 91 CHN-SHIC (上海國際賽車場) Shanghai Tianma Circuit 15 Asia China 92 CHN-TIAN (上海天馬山賽車場) Jiangsu Wantrack International Circuit 16 Asia China 93 CHN-WAN (江蘇萬馳國際賽車場) Xi'an Lintong Circuit 17 Asia China 2067 CHN-XLC (西安臨潼國際賽車場) Yunnan Trading Xiongfeng International Kart Field 18 Asia China 1062 CHN-YUN (雲南交投雄風卡丁車場) ZIC-Zhuhai International Circuit 19 Asia China 94 CHN-ZIC (珠海國際賽車場) Zhe Jiang Circuit 20 Asia China 95 CHN-ZJC (浙江国际赛车场) 21 Asia Indonesia 251 INA-SEN Sentul International Circuit 22 Asia Indonesia 252 INA-SENK Sentul Int'l Karting circuit 23 Asia India 253 IND-BUD Buddh International Circuit 24 Asia India 254 IND-KMS Kari Motor Speedway 25 Asia India 255 IND-MMS Madras Motor Sports Race Track 26 Asia Israel 713 ISR-PEZA Pezael Circuit Anti-Clockwise 1 Continent Country Track ID File Name Track Name NO. -

42 ENG PR 20171810 It F4 Championship
Press Release Number 42 / 2017 At the Monza Autodrome, 18 drivers took to the circuit for the third official test of the 2017 season In less than 48 hours – from Friday the 20th to Sunday the 22nd of October – the Brianza circuit will host the seventh and final round of the season. The fastest driver was Job Van Uitert Monza 18/10/2017 – Monza hosted the third and final official test of the 2017 Italian F4 Championship powered by Abarth season. It is here, from Friday the 20th through to Sunday the 22nd of October, that the closing round of the series will take place which will award the titles of both cham- pion driver and team. In the eight hours available – from 9:00am to 13:00 and from 14:00 through to 18:00 – there was two rivals for the title: the lea- der, the New Zealander Marcus Armstrong (Prema Power Team), who was fastest in the morning and the Dutch driver Job Van Uitert (Jenzer Motor- sport) the fastest in the afternoon session and indeed the fastest overall with a time of 1’53”151. As in previous official sessions, the drivers spared nothing with some completing more than 100 laps, a testament to the relia- bility of the single-seater cars powered by Abarth and using Magigas fuel and Pirelli tyres. • Behind Van Uitert was his teammate, the Indian Kush Maini (1’53”219), Armstrong (1’53”235, time recorded in the morning), and the driver who took pole position here at Monza last year, the Venezuelan Sebastian Fer- nandez (Bhaitech), with 1’53”365. -

FIA WORLD RALLY the FIA to Seek Alternatives the PART of the RALLY CHAMPIONSHIP to the Fixtures That Had to Be THAT TAKES PLACE - " Cancelled
raceguide 2020 Michelin AUTODROMO NAZIONALE DI MONZA (ITA LY) ACI RALLY2020 MONZA DECEMBER 3»6 Rally Monza didn’t figure on the original 2020 WRC - calendar but the pandemic forced the promoter and ROUND 7 2020 FIA WORLD RALLY the FIA to seek alternatives THE PART OF THE RALLY CHAMPIONSHIP to the fixtures that had to be THAT TAKES PLACE - " cancelled. The part of the rally ORGANISED BY AT THE CIRCUIT ITSELF WILL AUTOMOBILE CLUB ITALIA that takes place at the circuit BE A BIG CHALLENGE itself will be a big challenge in terms of tyre management as the track surface’s unique characteristics clearly differ from those of ordinary roads. The weather MICHELIN at this time of year could bring some surprises, so Arnaud Rémy this has the makings of being a very interesting AND RALLY MONZA WRC Programme Manager Michelin Motorsport event that will put tyre strategy at the centre of conversations once more as we wrap up the season. MICHELIN’S TYRES FOR THE 2020 RALLY MONZA michelin pilot sport pilot alpin The first Rally Monza to qualify for the FIA WRC Held at the Autodromo Nazionale di H5 S6 fw3 A4 (soft) (rain) non-studded Monza since 1978 (hard) WRC Since 2000, the event has taken the form of a year-ending ‘Rally Show’ 3 Michelin has contested the Monza Allocation: Drivers may use up to 28 tyres from an overall allocation of 24 H5s, 18 S6s, 12 FW3s and 8 A4s. Rally Show on numerous occasions with its factory partners Michelin Pilot Sport R33 (hard), RS (soft) Michelin won the Monza Rally Michelin Pilot Sport A MW1 (rain) Show in 2011 (with Sébastien Loeb) Michelin Pilot Alpin NA00 (non studded) and 2013 (Dani Sordo) 3 Allocation: Drivers may use up to 26 tyres from an The 2020 Rally Monza sees Michelin WRC2 overall allocation of 22 R33s, 16 RSs, 12 A MW1s and 8 NA00s. -

Instruction Booklet This Seal Is Your Assurance That Nintendo Has Approved the Quality of This Product
INSTRUCTION BOOKLET THIS SEAL IS YOUR ASSURANCE THAT NINTENDO HAS APPROVED THE QUALITY OF THIS PRODUCT. ALWAYS LOOK FOR THIS SEAL WHEN BUYING GAMES AND ACCESSORIES TO ENSURE COMPLETE COMPATIBILITY WITH YOUR NINTENDO SYSTEM. WARNING: Please carefully read the separate Health and Safety Precautions Booklet included with this product before using your Nintendo® Hardware system, Disc or Accessory. The booklet contains important safety information. THIS GAME SUPPORTS 50Hz (576i) AND 60Hz (480i) MODE. Modes Supported IMPORTANT LEGAL INFORMATION THIS NINTENDO GAME IS NOT DESIGNED FOR USE WITH ANY UNAUTHORISED DEVICE. USE OF ANY SUCH DEVICE WILL INVALIDATE YOUR NINTENDO PRODUCT WARRANTY. COPYING OF ANY NINTENDO GAME IS ILLEGAL AND IS STRICTLY PROHIBITED BY DOMESTIC AND INTERNATIONAL INTELLECTUAL PROPERTY LAWS. NINTENDO, Wii AND THE SEAL OF QUALITY ICON ARE TRADEMARKS OF NINTENDO. GETTING STARTED Insert the Ferrari Challenge-Trofeo Pirelli Disc into the Disc Slot. The Wii™ console will switch on. The Health and Safety Screen, as shown here, will be displayed. After reading the details press the A Button. The Health and Safety Screen will be displayed even if the Disc is inserted after turning the Wii console’s power on. Point at the Disc Channel from the Wii Menu Screen and press the A Button. The Channel Preview Screen will be displayed. Point at START and press the A Button. The Wii Remote™ Wrist Strap Information Screen will be displayed. Tighten the strap around your wrist, then press the A Button. The Title Screen will be displayed. System Menu Update Please note that when first loading the Disc into the Wii™ console, the console will check if you have the latest System Menu, and if necessary a Wii System Update Screen will appear. -

Crosslé Press Release
1 CROSSLÉ CAR COMPANY Press Release 13 November 2012 A New Chapter for The Crosslé Car Company The Crosslé Car Company Limited, the UK’s oldest constructor of racing cars, has announced exciting plans for its future. From Tuesday 13th November 2012, Arnie Black hands over ownership and management of the company to long-time Crosslé customer and enthusiast Paul McMorran. After thirty-two years as engineer and executive in the global oil industry, Paul brings a vibrant new approach to the business while safeguarding the values on which Crosslé was founded. A well-known competitor in historic racing across Europe, Paul’s collection of Crosslé cars includes the 12F that boosted exports by winning the US Formula B Championship in 1968, and the unique 1970 17F Formula 3 car originally raced by John Watson, Northern Ireland’s five-time Grand Prix winner. Paul drove the 17F to a podium finish at the Monaco Historic meeting in 2010. “I’m very excited by the opportunity to lead this iconic company. Historic motor racing continues to grow in popularity and Crosslé, with over fifty years of continuous manufacture, has a very special place in that history. The company continues to provide an unbroken link between the people who designed and built Crosslé cars here in Northern Ireland, and the many enthusiasts who continue to enjoy them worldwide. Crosslé has a famous past, a unique position in the market today, a great team of people and, I believe, a very bright future” said the new owner at the announcement. “This is wonderful news for the company and its staff,” said 2 Arnie Black, the multiple racing champion who took over ownership and management of the company in 1997 from its founder, Dr.