DOCSLIB.ORG

Saleh Faruque Radio Frequency Modulation Made Easy

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Saleh Faruque Radio Frequency Modulation Made Easy SPRINGER BRIEFS IN ELECTRICAL AND COMPUTER ENGINEERING Saleh Faruque Radio Frequency Modulation Made Easy 123 SpringerBriefs in Electrical and Computer Engineering More information about this series at http://www.springer.com/series/10059 Saleh Faruque Radio Frequency Modulation Made Easy 123 Saleh Faruque Department of Electrical Engineering University of North Dakota Grand Forks, ND USA ISSN 2191-8112 ISSN 2191-8120 (electronic) SpringerBriefs in Electrical and Computer Engineering ISBN 978-3-319-41200-9 ISBN 978-3-319-41202-3 (eBook) DOI 10.1007/978-3-319-41202-3 Library of Congress Control Number: 2016945147 © The Author(s) 2017 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. The publisher, the authors and the editors are safe to assume that the advice and information in this book are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or the editors give a warranty, express or implied, with respect to the material contained herein or for any errors or omissions that may have been made. Printed on acid-free paper This Springer imprint is published by Springer Nature The registered company is Springer International Publishing AG Switzerland Preface By inventing the wireless transmitter or radio in 1897, the Italian physicist Tomaso Guglielmo Marconi added a new dimension to the world of communications. This enabled the transmission of the human voice through space without wires. For this epoch-making invention, this illustrious scientist was honored with the Nobel Prize for Physics in 1909. Even today, students of wireless or radio technology remember this distinguished physicist with reverence. A new era began in Radio Communications. The classical Marconi radio used a modulation technique known today as “Amplitude Modulation” or just AM. This led to the development of Frequency Modulation (FM), amplitude shift keying (ASK), phase shift keying (PSK), etc. Today, these technologies are extensively used in various wireless communication systems. These modulation techniques form an integral part of academic curricula today. This book presents a comprehensive overview of the various modulation tech- niques mentioned above. Numerous illustrations are used to bring students up-to-date in key concepts and underlying principles of various analog and digital modulation techniques. In particular, the following topics will be presented in this book: • Amplitude Modulation (AM) • Frequency Modulation (FM) • Bandwidth occupancy in AM and FM • Amplitude shift keying (ASK) • Frequency shift keying (FSK) • Phase shift keying (PSK) • N-ary coding and M-ary modulation • Bandwidth occupancy in ASK, FSK, and PSK This text has been primarily designed for electrical engineering students in the area of telecommunications. However, engineers and designers working in the area v vi Preface of wireless communications would also find this text useful. It is assumed that the student is familiar with the general theory of telecommunications. In closing, I would like to say a few words about how this book was conceived. It came out of my long industrial and academic career. During my teaching tenure at the University of North Dakota, I developed a number of graduate-level elective courses in the area of telecommunications that combine theory and practice. This book is a collection of my courseware and research activities in wireless communications. I am grateful to UND and the School for the Blind, North Dakota, for affording me this opportunity. This book would never have seen the light of day had UND and the State of North Dakota not provided me with the technology to do so. My heartfelt salute goes out to the dedicated developers of these technologies, who have enabled me and others visually impaired to work comfortably. I would like to thank my beloved wife, Yasmin, an English Literature buff and a writer herself, for being by my side throughout the writing of this book and for patiently proofreading it. My darling son, Shams, an electrical engineer himself, provided technical support in formulation and experimentation when I needed it. For this, he deserves my heartfelt thanks. Finally, thanks are also to my doctoral student Md. Maruf Ahamed who found time in his busy schedule to assist me with the simulations, illustrations, and the verification of equations. In spite of all this support, there may still be some errors in this book. I hope that my readers forgive me for them. I shall be amply rewarded if they still find this book useful. Grand Forks, USA Saleh Faruque May 2016 Contents 1 Introduction to Modulation .............................. 1 1.1 Background . 1 1.2 Modulation by Analog Signals . 3 1.2.1 AM, FM, and PM . 3 1.2.2 AM and FM Bandwidth at a Glance . 4 1.3 Modulation by Digital Signal . 5 1.3.1 Amplitude Shift Keying (ASK) Modulation . 5 1.3.2 Frequency Shift Keying (FSK) Modulation. 6 1.3.3 Phase Shift Keying (PSK) Modulation . 7 1.4 Bandwidth Occupancy in Digital Modulation . 7 1.4.1 Spectral Response of the Encoded Data . 8 1.4.2 Spectral Response of the Carrier Frequency Before Modulation. 9 1.4.3 ASK Bandwidth at a Glance. 10 1.4.4 FSK Bandwidth at a Glance . 11 1.4.5 BPSK Bandwidth at a Glance. 12 1.5 Conclusions . 14 References . 15 2 Amplitude Modulation (AM) ............................. 17 2.1 Introduction . 17 2.2 Amplitude Modulation . 19 2.3 AM Spectrum and Bandwidth . 20 2.3.1 Spectral Response of the Input Modulating Signal. 20 2.3.2 Spectral Response of the Carrier Frequency . 21 2.3.3 AM Spectrum and Bandwidth. 21 2.3.4 AM Response Due to Low and High Modulating Signals . 23 2.3.5 AM Demodulation . 24 2.3.6 Drawbacks in AM. 24 vii viii Contents 2.4 Double Sideband-Suppressed Carrier (DSBSC) . 25 2.4.1 DSBSC Modulation. 25 2.4.2 Generation of DSBSC Signal . 26 2.4.3 DSBSC Spectrum and Bandwidth . 27 2.4.4 DSBSC Drawbacks . 28 2.5 Single Sideband (SSB) Modulation . 29 2.5.1 Why SSB Modulation? . 29 2.5.2 Generation of SSB-Modulated Signal. 29 2.5.3 SSB Spectrum and Bandwidth . 30 2.6 Conclusions . 32 References . 32 3 Frequency Modulation (FM) ............................. 33 3.1 Introduction . 33 3.2 Frequency Modulation (FM) . 34 3.2.1 Background . 34 3.2.2 The Basic FM . 35 3.3 FM Spectrum and Bandwidth . 37 3.3.1 Spectral Response of the Input Modulating Signal. 37 3.3.2 Spectral Response of the Carrier Frequency . 38 3.3.3 FM Spectrum . 39 3.3.4 Carson’s Rule and FM Bandwidth. 40 3.3.5 Bessel Function and FM Bandwidth . 41 3.3.6 FM Bandwidth Dilemma . 42 3.4 Conclusions . 44 References . 44 4 Amplitude Shift Keying (ASK) ............................ 45 4.1 Introduction . 45 4.2 ASK Modulation . 46 4.3 ASK Demodulation . 48 4.4 ASK Bandwidth . 49 4.4.1 Spectral Response of the Encoded Data . 49 4.4.2 Spectral Response of the Carrier Frequency Before Modulation. 51 4.4.3 ASK Bandwidth at a Glance. 51 4.5 BER Performance . 53 4.6 Conclusions . 54 References . 55 5 Frequency Shift Keying (FSK) ............................ 57 5.1 Introduction . 57 5.2 Frequency Shift Keying (FSK) Modulation. 58 5.3 Frequency Shift Keying (FSK) Demodulation . 60 Contents ix 5.4 FSK Bandwidth. 61 5.4.1 Spectral Response of the Encoded Data . 61 5.4.2 Spectral Response of the Carrier Frequency Before Modulation. 63 5.4.3 FSK Bandwidth at a Glance . 63 5.5 BER Performance . 65 5.6 Conclusions . 67 References . 67 6 Phase Shift Keying (PSK) ............................... 69 6.1 Introduction . 69 6.2 Binary Phase Shift Keying (BPSK) . 70 6.2.1 BPSK Modulation . 70 6.2.2 BPSK Demodulation . 73 6.3 QPSK Modulation . 74 6.4 8PSK Modulation . 75 6.5 16PSK Modulation . 75 6.6 PSK Spectrum and Bandwidth . 77 6.6.1 Spectral Response of the Encoded Data . 77 6.6.2 Spectral Response of the Carrier Before Modulation . 79 6.6.3 BPSK Spectrum . 79 6.7 Conclusions . 82 References . 82 7 N-Ary Coded Modulation................................ 85 7.1 Introduction . 85 7.2 N-Ary Convolutional Coding and M-Ary Modulation . 86 7.2.1 Background . 86 7.2.2 Generation of Complementary Convolutional Codes . ..
Load more

Recommended publications
  • Discrete Cosine Transform Based Image Fusion Techniques VPS Naidu MSDF Lab, FMCD, National Aerospace Laboratories, Bangalore, INDIA E.Mail: [email protected]
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by NAL-IR Journal of Communication, Navigation and Signal Processing (January 2012) Vol. 1, No. 1, pp. 35-45 Discrete Cosine Transform based Image Fusion Techniques VPS Naidu MSDF Lab, FMCD, National Aerospace Laboratories, Bangalore, INDIA E.mail: [email protected] Abstract: Six different types of image fusion algorithms based on 1 discrete cosine transform (DCT) were developed and their , k 1 0 performance was evaluated. Fusion performance is not good while N Where (k ) 1 and using the algorithms with block size less than 8x8 and also the block 1 2 size equivalent to the image size itself. DCTe and DCTmx based , 1 k 1 N 1 1 image fusion algorithms performed well. These algorithms are very N 1 simple and might be suitable for real time applications. 1 , k 0 Keywords: DCT, Contrast measure, Image fusion 2 N 2 (k 1 ) I. INTRODUCTION 2 , 1 k 2 N 2 1 Off late, different image fusion algorithms have been developed N 2 to merge the multiple images into a single image that contain all useful information. Pixel averaging of the source images k 1 & k 2 discrete frequency variables (n1 , n 2 ) pixel index (the images to be fused) is the simplest image fusion technique and it often produces undesirable side effects in the fused image Similarly, the 2D inverse discrete cosine transform is defined including reduced contrast. To overcome this side effects many as: researchers have developed multi resolution [1-3], multi scale [4,5] and statistical signal processing [6,7] based image fusion x(n1 , n 2 ) (k 1 ) (k 2 ) N 1 N 1 techniques.
    [Show full text]
  • Digital Signals
    Technical Information Digital Signals 1 1 bit t Part 1 Fundamentals Technical Information Part 1: Fundamentals Part 2: Self-operated Regulators Part 3: Control Valves Part 4: Communication Part 5: Building Automation Part 6: Process Automation Should you have any further questions or suggestions, please do not hesitate to contact us: SAMSON AG Phone (+49 69) 4 00 94 67 V74 / Schulung Telefax (+49 69) 4 00 97 16 Weismüllerstraße 3 E-Mail: [email protected] D-60314 Frankfurt Internet: http://www.samson.de Part 1 ⋅ L150EN Digital Signals Range of values and discretization . 5 Bits and bytes in hexadecimal notation. 7 Digital encoding of information. 8 Advantages of digital signal processing . 10 High interference immunity. 10 Short-time and permanent storage . 11 Flexible processing . 11 Various transmission options . 11 Transmission of digital signals . 12 Bit-parallel transmission. 12 Bit-serial transmission . 12 Appendix A1: Additional Literature. 14 99/12 ⋅ SAMSON AG CONTENTS 3 Fundamentals ⋅ Digital Signals V74/ DKE ⋅ SAMSON AG 4 Part 1 ⋅ L150EN Digital Signals In electronic signal and information processing and transmission, digital technology is increasingly being used because, in various applications, digi- tal signal transmission has many advantages over analog signal transmis- sion. Numerous and very successful applications of digital technology include the continuously growing number of PCs, the communication net- work ISDN as well as the increasing use of digital control stations (Direct Di- gital Control: DDC). Unlike analog technology which uses continuous signals, digital technology continuous or encodes the information into discrete signal states (Fig. 1). When only two discrete signals states are assigned per digital signal, these signals are termed binary si- gnals.
    [Show full text]
  • Radio Frequency Interference Analysis of Spectra from the Big Blade Antenna at the LWDA Site
    Radio Frequency Interference Analysis of Spectra from the Big Blade Antenna at the LWDA Site Robert Duffin (GMU/NRL) and Paul S. Ray (NRL) March 23, 2007 Introduction The LWA analog receiver will be required to amplify and digitize RF signals over the full bandwidth of at least 20–80 MHz. This frequency range is populated with a number of strong sources of radio frequency interference (RFI), including several TV stations, HF broadcast transmissions, ham radio, and is adjacent to the FM band. Although filtering can be used to attenuate signals outside the band, the receiver must be designed with sufficient linearity and dynamic range to observe cosmic sources in the unoccupied regions between the, typically narrowband, RFI signals. A receiver of insufficient linearity will generate inter-modulation products at frequencies in the observing bands that will make it difficult or impossible to accomplish the science objectives. On the other hand, over-designing the receiver is undesirable because any excess cost or power usage will be multiplied by the 26,000 channels in the full design and may make the project unfeasible. Since the sky background is low level and broadband, the linearity requirements primarily depend on the RFI signals presented to the receiver. Consequently, a detailed study of the RFI environment at candidate LWA sites is essential. Often RFI surveys are done using antennas optimized for RFI detection such as discone antennas. However, such data are of limited usefulness for setting the receiver requirements because what is relevant is what signals are passed to the receiver when it is connected to the actual LWA antenna.
    [Show full text]
  • Microwave Frequency Demodulation Using Two Coupled Optical Resonators with Modulated Refractive Index
    PHYSICAL REVIEW APPLIED 15, 034056 (2021) Microwave Frequency Demodulation Using two Coupled Optical Resonators with Modulated Refractive Index Adam Mock * School of Engineering and Technology, Central Michigan University, Mount Pleasant, Michigan 48859, USA (Received 16 October 2020; revised 1 February 2021; accepted 10 February 2021; published 18 March 2021) Traditional electronic frequency demodulation of a microwave frequency voltage is challenging because it requires complicated phase-locked loops, narrowband filters with fixed passbands, or large footprint local oscillators and mixers. Herein, a different frequency demodulation concept is proposed based on refractive index modulation of two coupled microcavities excited by an optical wave. A frequency- modulated microwave frequency voltage is applied to two photonic crystal microcavities in a spatially odd configuration. The spatially odd perturbation causes coupling between the even and odd supermodes of the coupled-cavity system. It is shown theoretically and verified by finite-difference time-domain sim- ulations how careful choice of the modulation amplitude and frequency can switch the optical output from on to off. As the modulating frequency is detuned from its off value, the optical output switches from off to on. Ultimately, the optical output amplitude is proportional to the frequency deviation of the applied voltage making this device a frequency-modulated-voltage to amplitude-modulated-optical- wave converter. The optical output can be immediately detected and converted to a voltage that would result in a frequency-demodulated voltage signal. Or the optical output can be fed into a larger radio- over-fiber optical network. In this case the device presents a compact, low power, and tunable route for multiplexing frequency-modulated voltages with amplitude-modulated optical communication systems.
    [Show full text]
  • How I Came up with the Discrete Cosine Transform Nasir Ahmed Electrical and Computer Engineering Department, University of New Mexico, Albuquerque, New Mexico 87131
    mxT*L. BImL4L. PRocEsSlNG 1,4-5 (1991) How I Came Up with the Discrete Cosine Transform Nasir Ahmed Electrical and Computer Engineering Department, University of New Mexico, Albuquerque, New Mexico 87131 During the late sixties and early seventies, there to study a “cosine transform” using Chebyshev poly- was a great deal of research activity related to digital nomials of the form orthogonal transforms and their use for image data compression. As such, there were a large number of T,(m) = (l/N)‘/“, m = 1, 2, . , N transforms being introduced with claims of better per- formance relative to others transforms. Such compari- em- lh) h = 1 2 N T,(m) = (2/N)‘%os 2N t ,...) . sons were typically made on a qualitative basis, by viewing a set of “standard” images that had been sub- jected to data compression using transform coding The motivation for looking into such “cosine func- techniques. At the same time, a number of researchers tions” was that they closely resembled KLT basis were doing some excellent work on making compari- functions for a range of values of the correlation coef- sons on a quantitative basis. In particular, researchers ficient p (in the covariance matrix). Further, this at the University of Southern California’s Image Pro- range of values for p was relevant to image data per- cessing Institute (Bill Pratt, Harry Andrews, Ali Ha- taining to a variety of applications. bibi, and others) and the University of California at Much to my disappointment, NSF did not fund the Los Angeles (Judea Pearl) played a key role.
    [Show full text]
  • Digital Audio Broadcasting : Principles and Applications of Digital Radio
    Digital Audio Broadcasting Principles and Applications of Digital Radio Second Edition Edited by WOLFGANG HOEG Berlin, Germany and THOMAS LAUTERBACH University of Applied Sciences, Nuernberg, Germany Digital Audio Broadcasting Digital Audio Broadcasting Principles and Applications of Digital Radio Second Edition Edited by WOLFGANG HOEG Berlin, Germany and THOMAS LAUTERBACH University of Applied Sciences, Nuernberg, Germany Copyright ß 2003 John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England Telephone (þ44) 1243 779777 Email (for orders and customer service enquiries): [email protected] Visit our Home Page on www.wileyeurope.com or www.wiley.com All Rights Reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except under the terms of the Copyright, Designs and Patents Act 1988 or under the terms of a licence issued by the Copyright Licensing Agency Ltd, 90 Tottenham Court Road, London W1T 4LP, UK, without the permission in writing of the Publisher. Requests to the Publisher should be addressed to the Permissions Department, John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England, or emailed to [email protected], or faxed to (þ44) 1243 770571. This publication is designed to provide accurate and authoritative information in regard to the subject matter covered. It is sold on the understanding that the Publisher is not engaged in rendering professional services. If professional advice or other expert assistance is required, the services of a competent professional should be sought.
    [Show full text]
  • History of Radio Broadcasting in Montana
    University of Montana ScholarWorks at University of Montana Graduate Student Theses, Dissertations, & Professional Papers Graduate School 1963 History of radio broadcasting in Montana Ron P. Richards The University of Montana Follow this and additional works at: https://scholarworks.umt.edu/etd Let us know how access to this document benefits ou.y Recommended Citation Richards, Ron P., "History of radio broadcasting in Montana" (1963). Graduate Student Theses, Dissertations, & Professional Papers. 5869. https://scholarworks.umt.edu/etd/5869 This Thesis is brought to you for free and open access by the Graduate School at ScholarWorks at University of Montana. It has been accepted for inclusion in Graduate Student Theses, Dissertations, & Professional Papers by an authorized administrator of ScholarWorks at University of Montana. For more information, please contact [email protected]. THE HISTORY OF RADIO BROADCASTING IN MONTANA ty RON P. RICHARDS B. A. in Journalism Montana State University, 1959 Presented in partial fulfillment of the requirements for the degree of Master of Arts in Journalism MONTANA STATE UNIVERSITY 1963 Approved by: Chairman, Board of Examiners Dean, Graduate School Date Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. UMI Number; EP36670 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a complete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. UMT Oiuartation PVUithing UMI EP36670 Published by ProQuest LLC (2013).
    [Show full text]
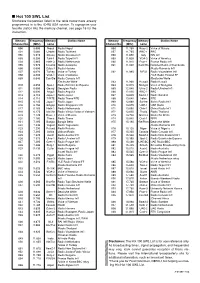
  • Hot 100 SWL List Shortwave Frequencies Listed in the Table Below Have Already Programmed in to the IC-R5 USA Version
    I Hot 100 SWL List Shortwave frequencies listed in the table below have already programmed in to the IC-R5 USA version. To reprogram your favorite station into the memory channel, see page 16 for the instruction. Memory Frequency Memory Station Name Memory Frequency Memory Station Name Channel No. (MHz) name Channel No. (MHz) name 000 5.005 Nepal Radio Nepal 056 11.750 Russ-2 Voice of Russia 001 5.060 Uzbeki Radio Tashkent 057 11.765 BBC-1 BBC 002 5.915 Slovak Radio Slovakia Int’l 058 11.800 Italy RAI Int’l 003 5.950 Taiw-1 Radio Taipei Int’l 059 11.825 VOA-3 Voice of America 004 5.965 Neth-3 Radio Netherlands 060 11.910 Fran-1 France Radio Int’l 005 5.975 Columb Radio Autentica 061 11.940 Cam/Ro National Radio of Cambodia 006 6.000 Cuba-1 Radio Havana /Radio Romania Int’l 007 6.020 Turkey Voice of Turkey 062 11.985 B/F/G Radio Vlaanderen Int’l 008 6.035 VOA-1 Voice of America /YLE Radio Finland FF 009 6.040 Can/Ge Radio Canada Int’l /Deutsche Welle /Deutsche Welle 063 11.990 Kuwait Radio Kuwait 010 6.055 Spai-1 Radio Exterior de Espana 064 12.015 Mongol Voice of Mongolia 011 6.080 Georgi Georgian Radio 065 12.040 Ukra-2 Radio Ukraine Int’l 012 6.090 Anguil Radio Anguilla 066 12.095 BBC-2 BBC 013 6.110 Japa-1 Radio Japan 067 13.625 Swed-1 Radio Sweden 014 6.115 Ti/RTE Radio Tirana/RTE 068 13.640 Irelan RTE 015 6.145 Japa-2 Radio Japan 069 13.660 Switze Swiss Radio Int’l 016 6.150 Singap Radio Singapore Int’l 070 13.675 UAE-1 UAE Radio 017 6.165 Neth-1 Radio Netherlands 071 13.680 Chin-1 China Radio Int’l 018 6.175 Ma/Vie Radio Vilnius/Voice
    [Show full text]
  • Radio Broadcasting
    Programs of Study Leading to an Associate Degree or R-TV 15 Broadcast Law and Business Practices 3.0 R-TV 96C Campus Radio Station Lab: 1.0 of Radiologic Technology. This is a licensed profession, CHLD 10H Child Growth 3.0 R-TV 96A Campus Radio Station Lab: Studio 1.0 Hosting and Management Skills and a valid Social Security number is required to obtain and Lifespan Development - Honors Procedures and Equipment Operations R-TV 97A Radio/Entertainment Industry 1.0 state certification and national licensure. or R-TV 96B Campus Radio Station Lab: Disc 1.0 Seminar Required Courses: PSYC 14 Developmental Psychology 3.0 Jockey & News Anchor/Reporter Skills R-TV 97B Radio/Entertainment Industry 1.0 RAD 1A Clinical Experience 1A 5.0 and R-TV 96C Campus Radio Station Lab: Hosting 1.0 Work Experience RAD 1B Clinical Experience 1B 3.0 PSYC 1A Introduction to Psychology 3.0 and Management Skills Plus 6 Units from the following courses (6 Units) RAD 2A Clinical Experience 2A 5.0 or R-TV 97A Radio/Entertainment Industry Seminar 1.0 R-TV 03 Sportscasting and Reporting 1.5 RAD 2B Clinical Experience 2B 3.0 PSYC 1AH Introduction to Psychology - Honors 3.0 R-TV 97B Radio/Entertainment Industry 1.0 R-TV 04 Broadcast News Field Reporting 3.0 RAD 3A Clinical Experience 3A 7.5 and Work Experience R-TV 06 Broadcast Traffic Reporting 1.5 RAD 3B Clinical Experience 3B 3.0 SPCH 1A Public Speaking 4.0 Plus 6 Units from the Following Courses: 6 Units: R-TV 09 Broadcast Sales and Promotion 3.0 RAD 3C Clinical Experience 3C 7.5 or R-TV 05 Radio-TV Newswriting 3.0
    [Show full text]
  • A Guide for Radio Operators BROCHURE RADIO TRANSM ANG 3/27/97 8:47 PM Page 2
    BROCHURE RADIO TRANSM ANG 3/27/97 8:47 PM Page 17 A Guide for Radio Operators BROCHURE RADIO TRANSM ANG 3/27/97 8:47 PM Page 2 Aussi disponible en français. 32-EN-95539W-01 © Minister of Public Works and Government Services Canada 1996 BROCHURE RADIO TRANSM ANG 3/27/97 8:47 PM Page 3 CUTTING THROUGH... INTERFERENCE FROM RADIO TRANSMITTERS A Guide for Radio Operators This brochure is primarily for amateur and General Radio Service (GRS, commonly known as CB) radio operators. It provides basic information to help you install and maintain your station so you get the best performance and the most enjoyment from it. You will learn how to identify the causes of radio interference in nearby electronic equipment, and how to fix the problem. What type of equipment can be affected by radio interference? Both radio and non-radio devices can be adversely affected by radio signals. Radio devices include AM and FM radios, televisions, cordless telephones and wireless intercoms. Non-radio electronic equipment includes stereo audio systems, wired telephones and regular wired intercoms. All of this equipment can be disturbed by radio signals. What can cause radio interference? Interference usually occurs when radio transmitters and electronic equipment are operated within close range of each other. Interference is caused by: ■ incorrectly installed radio transmitting equipment; ■ an intense radio signal from a nearby transmitter; ■ unwanted signals (called spurious radiation) generated by the transmitting equipment; and ■ not enough shielding or filtering in the electronic equipment to prevent it from picking up unwanted signals. What can you do? 1.
    [Show full text]
  • Reception Performance Improvement of AM/FM Tuner by Digital Signal Processing Technology
    Reception performance improvement of AM/FM tuner by digital signal processing technology Akira Hatakeyama Osamu Keishima Kiyotaka Nakagawa Yoshiaki Inoue Takehiro Sakai Hirokazu Matsunaga Abstract With developments in digital technology, CDs, MDs, DVDs, HDDs and digital media have become the mainstream of car AV products. In terms of broadcasting media, various types of digital broadcasting have begun in countries all over the world. Thus, there is a demand for smaller and thinner products, in order to enhance radio performance and to achieve consolidation with the above-mentioned digital media in limited space. Due to these circumstances, we are attaining such performance enhancement through digital signal processing for AM/FM IF and beyond, and both tuner miniaturization and lighter products have been realized. The digital signal processing tuner which we will introduce was developed with Freescale Semiconductor, Inc. for the 2005 line model. In this paper, we explain regarding the function outline, characteristics, and main tech- nology involved. 22 Reception performance improvement of AM/FM tuner by digital signal processing technology Introduction1. Introduction from IF signals, interference and noise prevention perfor- 1 mance have surpassed those of analog systems. In recent years, CDs, MDs, DVDs, and digital media have become the mainstream in the car AV market. 2.2 Goals of digitalization In terms of broadcast media, with terrestrial digital The following items were the goals in the develop- TV and audio broadcasting, and satellite broadcasting ment of this digital processing platform for radio: having begun in Japan, while overseas DAB (digital audio ①Improvements in performance (differentiation with broadcasting) is used mainly in Europe and SDARS (satel- other companies through software algorithms) lite digital audio radio service) and IBOC (in band on ・Reduction in noise (improvements in AM/FM noise channel) are used in the United States, digital broadcast- reduction performance, and FM multi-pass perfor- ing is expected to increase in the future.
    [Show full text]
  • Additive Synthesis, Amplitude Modulation and Frequency Modulation
    Additive Synthesis, Amplitude Modulation and Frequency Modulation Prof Eduardo R Miranda Varèse-Gastprofessor [email protected] Electronic Music Studio TU Berlin Institute of Communications Research http://www.kgw.tu-berlin.de/ Topics: Additive Synthesis Amplitude Modulation (and Ring Modulation) Frequency Modulation Additive Synthesis • The technique assumes that any periodic waveform can be modelled as a sum sinusoids at various amplitude envelopes and time-varying frequencies. • Works by summing up individually generated sinusoids in order to form a specific sound. Additive Synthesis eg21 Additive Synthesis eg24 • A very powerful and flexible technique. • But it is difficult to control manually and is computationally expensive. • Musical timbres: composed of dozens of time-varying partials. • It requires dozens of oscillators, noise generators and envelopes to obtain convincing simulations of acoustic sounds. • The specification and control of the parameter values for these components are difficult and time consuming. • Alternative approach: tools to obtain the synthesis parameters automatically from the analysis of the spectrum of sampled sounds. Amplitude Modulation • Modulation occurs when some aspect of an audio signal (carrier) varies according to the behaviour of another signal (modulator). • AM = when a modulator drives the amplitude of a carrier. • Simple AM: uses only 2 sinewave oscillators. eg23 • Complex AM: may involve more than 2 signals; or signals other than sinewaves may be employed as carriers and/or modulators. • Two types of AM: a) Classic AM b) Ring Modulation Classic AM • The output from the modulator is added to an offset amplitude value. • If there is no modulation, then the amplitude of the carrier will be equal to the offset.
    [Show full text]