Assessing Regional Scale Weed Distributions, with an Australian Example Using Nassella Trichotoma
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Water Recycling in Australia (Report)
WATER RECYCLING IN AUSTRALIA A review undertaken by the Australian Academy of Technological Sciences and Engineering 2004 Water Recycling in Australia © Australian Academy of Technological Sciences and Engineering ISBN 1875618 80 5. This work is copyright. Apart from any use permitted under the Copyright Act 1968, no part may be reproduced by any process without written permission from the publisher. Requests and inquiries concerning reproduction rights should be directed to the publisher. Publisher: Australian Academy of Technological Sciences and Engineering Ian McLennan House 197 Royal Parade, Parkville, Victoria 3052 (PO Box 355, Parkville Victoria 3052) ph: +61 3 9347 0622 fax: +61 3 9347 8237 www.atse.org.au This report is also available as a PDF document on the website of ATSE, www.atse.org.au Authorship: The Study Director and author of this report was Dr John C Radcliffe AM FTSE Production: BPA Print Group, 11 Evans Street Burwood, Victoria 3125 Cover: - Integrated water cycle management of water in the home, encompassing reticulated drinking water from local catchment, harvested rainwater from the roof, effluent treated for recycling back to the home for non-drinking water purposes and environmentally sensitive stormwater management. – Illustration courtesy of Gold Coast Water FOREWORD The Australian Academy of Technological Sciences and Engineering is one of the four national learned academies. Membership is by nomination and its Fellows have achieved distinction in their fields. The Academy provides a forum for study and discussion, explores policy issues relating to advancing technologies, formulates comment and advice to government and to the community on technological and engineering matters, and encourages research, education and the pursuit of excellence. -

Ace Works Layout
South East Australian Transport Strategy Inc. SEATS A Strategic Transport Network for South East Australia SEATS’ holistic approach supports economic development FTRUANNSDPOINRTG – JTOHBSE – FLIUFETSUTYRLE E 2013 SEATS South East Australian Transport Strategy Inc. Figure 1. The SEATS region (shaded green) Courtesy Meyrick and Associates Written by Ralf Kastan of Kastan Consulting for South East Australian Transport Strategy Inc (SEATS), with assistance from SEATS members (see list of members p.52). Edited by Laurelle Pacey Design and Layout by Artplan Graphics Published May 2013 by SEATS, PO Box 2106, MALUA BAY NSW 2536. www.seats.org.au For more information, please contact SEATS Executive Officer Chris Vardon OAM Phone: (02) 4471 1398 Mobile: 0413 088 797 Email: [email protected] Copyright © 2013 SEATS - South East Australian Transport Strategy Inc. 2 A Strategic Transport Network for South East Australia Contents MAP of SEATS region ......................................................................................................................................... 2 Executive Summary and proposed infrastructure ............................................................................ 4 1. Introduction ................................................................................................................................................. 6 2. Network objectives ............................................................................................................................... 7 3. SEATS STRATEGIC NETWORK ............................................................................................................ -

2015/16 Annual Review
ANNUAL REVIEW 15/16 PMS > CMYK > REVERSED > PROVIDING REGIONAL WATER AUTHORITIES WITH INDEPENDENT, EXPERT ADVICE, TECHNICAL SUPPORT, SHARED INDUSTRY KNOWLEDGE, IMPROVED EFFICIENCIES AND LONG TERM PLANNING. CHAIR’S REVIEW In 2015/16 the Water Directorate made notable is the eleventh Executive Committee member advances in the face of change and challenges. to reach this milestone. Very special mention The year commenced with NSW Office of Water goes to Wayne Beatty, Water and Sewerage advising its new name of DPI Water and that Strategic Manager at Orange City Council, for it will focus on water planning and policy in his dedicated support of the Water Directorate. urban and rural areas, and will also oversee At the March Executive Committee meeting I government funded water infrastructure presented Wayne with a 15-year medallion and programs and develop more information on thanked him and Orange City Council for his water for the community. Final structural input and advised that Wayne is only the fourth arrangements and the impact on urban water Executive Committee member to achieve this branch within DPI Water are still being resolved. significant milestone. Highest number of members yet Important links with the wider water industry I was extremely pleased when the 98th council In these interesting times we place great value joined the Water Directorate: our highest level of on our relationships with Local Government membership in 18 years. We appreciate this show NSW, IPWEA, AWA, WSAA and WIOA. of support from our member councils throughout On a lighter note, at the WIOA Conference in 2015/16. Representation is 96% of the102 NSW Newcastle, Nambucca Shire Council was judged local water utilities - but ironically this milestone to have the best tasting NSW water in 2016. -

Government Gazette of the STATE of NEW SOUTH WALES Number 108 Friday, 27 August 2010 Published Under Authority by Government Advertising
3995 Government Gazette OF THE STATE OF NEW SOUTH WALES Number 108 Friday, 27 August 2010 Published under authority by Government Advertising LEGISLATION Online notification of the making of statutory instruments Week beginning 16 August 2010 THE following instruments were officially notified on the NSW legislation website (www.legislation.nsw.gov.au) on the dates indicated: Proclamations commencing Acts Food Amendment (Beef Labelling) Act 2009 No 120 (2010-462) — published LW 20 August 2010 Regulations and other statutory instruments Children and Young Persons (Care and Protection) (Child Employment) Regulation 2010 (2010-441) — published LW 20 August 2010 Crimes (Interstate Transfer of Community Based Sentences) Regulation 2010 (2010-443) — published LW 20 August 2010 Crimes Regulation 2010 (2010-442) — published LW 20 August 2010 Exhibited Animals Protection Regulation 2010 (2010-444) — published LW 20 August 2010 Food Amendment (Beef Labelling) Regulation 2010 (2010-463) — published LW 20 August 2010 Library Regulation 2010 (2010-445) — published LW 20 August 2010 Property (Relationships) Regulation 2010 (2010-446) — published LW 20 August 2010 Public Sector Employment and Management (General Counsel of DPC) Order 2010 (2010-447) — published LW 20 August 2010 Public Sector Employment and Management (Goods and Services) Regulation 2010 (2010-448) — published LW 20 August 2010 Road Transport (Vehicle Registration) Amendment (Number-Plates) Regulation 2010 (2010-449) — published LW 20 August 2010 State Records Regulation 2010 (2010-450) -

2014/15 Annual Review
ANNUAL REVIEW 14PMS > /15 CMYK > Providing regional water authorities REVERSEDwith independent, > expert advice, technical support, shared industry knowledge, improved efficiencies and long term planning. Chair & Executive Officer Review CHAIR REVIEW EXECUTIVE OFFICER REVIEW As my first full year as Chair, I am pleased to The release of the 2013-14 NSW Water Supply report that we have continued to strengthen and Sewerage Performance Monitoring Report our position as the leading technical shows that NSW LWUs continue to lead the association for NSW local water utilities. way nationally in providing safe and affordable water and sewer services for regional NSW. The In November we held the Local Water Utilities outstanding performance of LWUs is highlighted Regulations Workshop in response to the NSW in this annual review. Government’s Fit for the Future discussion paper. The workshop was well attended and The results of an occupational profile survey developed a number of Heads of Consideration undertaken by the NSW Public Sector ITAB on for the regulation. Formal discussions are behalf of the Water Directorate this year are also now underway with senior staff of the Office of highlighted in this annual review. The survey Local Government regarding these outcomes. determined the number of employees in the water occupations as defined in the Australian Water In December the Water Directorate and WSAA Occupations Framework. signed an MOU establishing opportunities for our members and reinforcing our commitment Over the past year we have concentrated on to work together as advocates for the water continuing to produce high quality technical industry. documents including: a revised Blue-Green Algae Action Flowchart; a new technical document Previously I indicated that a major focus for Guidelines for Trenchless Installation, Replacement this year would be the update of our extensive or Rehabilitation; and the Easement Guidelines suite of manuals and guidelines. -

List of Successful Round 2 and Round 2.5 Projects
Fixing Country Roads Rounds 2 & 2.5 Successful Projects List Fixing Country Roads Round 2 Local Government Area(s) Project Name Funding Amount Armidale Dumaresq Council Armidale Dumaresq Council Level 3 Bridge (Now Armidale Regional $95,000 Inspections Council) Bellingen Shire Timber Bridge Capacity Bellingen Shire Council $135,000 Assessment Bombala Shire Council (now Rosemeath Road Widening and Pavement Snowy Monaro Regional $375,000 Strengthening Council) Bombala Shire Council (now Snowy Monaro Regional Upgrade of Regional Tantawangalo Road $150,000 Council) MR 241 Murringo Road Pavement Widening Boorowa Council (now at 3.25-3.75km and 8-8.9km West of Lachlan $461,000 Hilltops Council) Valley Way Boorowa Council (now MR 380 Cunningar Road Pavement $960,000 Hilltops Council) Rehabilitation and Widening Eyre/Comstock and Comstock//Patton Street Broken Hill City Council $700,000 Intersection Concrete Upgrade Clarence Valley Council Jacks Bridge Replacement $40,000 Clarence Valley Council Kinghorn Bridge Replacement $175,000 Clarence Valley Council Romiaka Channel Bridge Replacement $1,731,000 Cobar Shire Council Seal extension Wilga Downs Road (SR26) $800,000 Coffs Harbour City Council Rebuilding Taylors Bridge $180,000 Validation of maximum load limits for Coffs Coffs Harbour City Council $175,000 Harbour City Council Regional Road Bridges Coolamon Shire Council Ardlethan Grain Hub Connectivity Project $666,300 Cooma Monaro Shire Council (now Snowy Monaro Cooma Monaro Shire Bridge Assessment $184,000 Regional Council) Cooma Monaro Shire -

PUBLISHED VERSION Beer, Andrew; Tually, Selina; Rowley, Steven; Haslam Mckenzie, Fiona; Schlapp, Julia; Birdsall-Jones, Christi
PUBLISHED VERSION Beer, Andrew; Tually, Selina; Rowley, Steven; Haslam McKenzie, Fiona; Schlapp, Julia; Birdsall-Jones, Christina; Corunna, Vanessa The drivers of supply and demand in Australia's rural and regional centres AHURI Final Report, 2011; No.165:1-127 © 2013 AHURI http://www.ahuri.edu.au/publications/download/ahuri_40586_fr PERMISSIONS As per email correspondence from AHURI : Received: Friday 28 June 2013 1:29 PM http://hdl.handle.net/2440/73162 The drivers of supply and demand in Australia’s rural and regional centres authored by Andrew Beer, Selina Tually, Steven Rowley, Fiona Haslam McKenzie, Julia Schlapp, Christina Birdsall Jones and Vanessa Corunna for the Australian Housing and Urban Research Institute Southern Research Centre Western Australia Research Centre RMIT Research Centre March 2011 AHURI Final Report No. 165 ISSN: 1834-7223 ISBN: 978-1-921610-66-0 Authors Beer, Andrew University of Adelaide Tually, Selina University of Adelaide Rowley, Steven Curtin University Haslam McKenzie, Fiona Curtin University Schlapp, Julia RMIT University Birdsall-Jones, Christina Curtin University Corunna, Vanessa Curtin University Title The drivers of supply and demand in Australia’s rural and regional centres ISBN 978-1-921610-66-0 Format PDF Key Words driver, supply, demand, Australia, rural, regional, centre Editor Jim Davison AHURI National Office Publisher Australian Housing and Urban Research Institute Melbourne, Australia Series AHURI Final Report; no.165 ISSN 1834-7223 Preferred Citation Beer, A. et al. (2011) The drivers of supply and demand in Australia’s rural and regional centres, AHURI Final Report No.165. Melbourne: Australian Housing and Urban Research Institute i ACKNOWLEDGEMENTS This material was produced with funding from the Australian Government and the Australian states and territory governments. -

Assessment of Council Fit for the Future Proposals: Appendix C
Assessment of Council Fit for the Future Proposals: Appendix C Local Government — Final Report October 2015 3 IPART’s assessment and decision 26 IPART North Sydney Council’s application for a special variation ALBURY CITY COUNCIL – CIP FIT Area (km2) 306 Population 2011 49,450 OLG Group 4 (2031) 56,950 ILGRP Group E Merger 2011 59,500 (2031) 66,900 Operating revenue $72.5m TCorp assessment Moderate FSR (2013-14) Neutral outlook ILGRP options Council in Upper Murray JO (all shaded) or merge with (no preference) Greater Hume (part or all) (yellow). Assessment summary Scale and capacity Satisfies Financial criteria: Satisfies overall Sustainability Satisfies Infrastructure and Satisfies service management Efficiency Satisfies Fit for the Future – FIT The council satisfies the scale and capacity criterion. The council satisfies the financial criteria overall. It satisfies the sustainability, infrastructure and service management and efficiency criteria. Scale and capacity – satisfies The council has a robust revenue base and is home to Albury, a large regional centre. Our analysis suggests this population is sufficient to enable the council to have the strategic capacity to meet the future needs of its community and be a capable partner in the regional area for government. The council’s proposal to stand alone in a JO is consistent with the ILGRP’s options for this council. The council indicates it is actively considering opportunities for an Upper Murray JO. The council rejected a proposal to merge and did not submit a merger business case. We do not have sufficient evidence to evaluate the costs and benefits of the merger option compared to the stand alone proposal. -

IPART Report Card
REPORT CARD IPART assessment of NSW council Fit for the Future proposals The Independent Pricing and Regulatory IPART assessed the proposals against Tribunal (IPART) has recently provided the the following criteria: NSW Government with its report on the • Scale and capacity assessment of 139 Fit for the Future council • Financial criteria proposals (received from 144 councils). - Financial sustainability This report card provides a snapshot of - Infrastructure and service what IPART found. management - Efficiency The IPART report clearly shows that the system of local government in NSW is broken. 60%Not fit 40%Fit “Our (IPART’s) analysis and Sydney metro merges could save close to the analysis undertaken by our independent economic consultants, Ernst & Young, indicated the merger option would provide large net benefits to the local communities.” $2billion *IPART 20-year NPV estimate usung standardised assumptions Assessment of Council Fit for the Future Proposals - p2 based on council consultant business cases - p40 Sydney metropolitan councils: Regional councils: 71% Not fit 56%Not fit This report card was produced by the Office of Local Government. The full IPART report can be found atwww.ipart.nsw.gov.au REPORT CARD - Key Findings Merger benefits - up to Councils prefered rate $2 billion rises to merging IPART conducted additional analysis on Many councils proposed rate increases to business cases submitted by councils and improve financial performance. Some 32 estimate between $1.8 billion to $2.0 billion in councils proposed a rate rise to get fit with 15 NPV benefits could be realised over 20 years councils proposing rises above 30%. if mergers were to occur in Sydney. -

18150 WD Annual Review 2012/2013
Annual Review 2012 /2013 Providing PMS > regional water authorities with indePendent, exPert advice, technical suPPort, shared industry knowledge, imProved efficiencies and long CMYK > term Planning REVERSED > Photos supplied courtesy of Water Directorate member councils. Chair Review In the absence a response from the a large number of members from representation opportunities more State Government regarding local different regions. However, our closely in the near future. water utility reform the Water strong membership base and good Once again I would like to thank the Directorate has remained focussed communication channels meant that on promoting the good work achieved we could consult widely with members members of the Executive Committee by local water utilities, particularly on the content of our submissions for their involvement in all our activities. since the introduction of the best prior to the closing dates. I particularly want to thank retiring practice framework by the NSW members Carmel Krogh and Simon Office of Water in 2007. A copy of our submissions to the State Thorn who have been stalwart members Infrastructure Strategy 2012-32, the of the Executive Committee over a In recent months we made Local Government Acts Taskforce, number of years. Their professionalism submissions to four separate the Joint Review of the Water and passion for the local government government inquiries that strongly Industry Competition Act 2006 and the water industry will be missed. promoted the benefit of water and/ Independent Local Government Review or sewerage services being delivered Most importantly I want to thank our by local water utilities. The Water Panel are available on our website. -
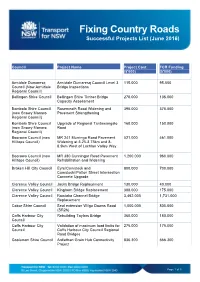
Fixing Country Roads Successful Projects List (June 2016)
Fixing Country Roads Successful Projects List (June 2016) Council Project Name Project Cost FCR Funding ($'000) ($'000) Armidale Dumaresq Armidale Dumaresq Council Level 3 115.000 95.000 Council (Now Armidale Bridge Inspections Regional Council) Bellingen Shire Council Bellingen Shire Timber Bridge 270.000 135.000 Capacity Assessment Bombala Shire Council Rosemeath Road Widening and 395.000 375.000 (now Snowy Monaro Pavement Strengthening Regional Council) Bombala Shire Council Upgrade of Regional Tantawangalo 160.000 150.000 (now Snowy Monaro Road Regional Council) Boorowa Council (now MR 241 Murringo Road Pavement 521.000 461.000 Hilltops Council) Widening at 3.25-3.75km and 8- 8.9km West of Lachlan Valley Way Boorowa Council (now MR 380 Cunningar Road Pavement 1,200.000 960.000 Hilltops Council) Rehabilitation and Widening Broken Hill City Council Eyre/Comstock and 800.000 700.000 Comstock//Patton Street Intersection Concrete Upgrade Clarence Valley Council Jacks Bridge Replacement 130.000 40.000 Clarence Valley Council Kinghorn Bridge Replacement 388.000 175.000 Clarence Valley Council Romiaka Channel Bridge 3,462.000 1,731.000 Replacement Cobar Shire Council Seal extension Wilga Downs Road 1,000.000 800.000 (SR26) Coffs Harbour City Rebuilding Taylors Bridge 360.000 180.000 Council Coffs Harbour City Validation of maximum load limits for 275.000 175.000 Council Coffs Harbour City Council Regional Road Bridges Coolamon Shire Council Ardlethan Grain Hub Connectivity 836.300 666.300 Project Page 1 of 5 Fixing Country Roads Successful -

Official Committee Hansard
COMMONWEALTH OF AUSTRALIA Official Committee Hansard HOUSE OF REPRESENTATIVES SELECT COMMITTEE ON THE RECENT AUSTRALIAN BUSHFIRES Reference: The recent Australian bushfires THURSDAY, 10 JULY 2003 COOMA BY AUTHORITY OF THE HOUSE OF REPRESENTATIVES INTERNET The Proof and Official Hansard transcripts of Senate committee hearings, some House of Representatives committee hearings and some joint committee hearings are available on the Internet. Some House of Representatives committees and some joint committees make available only Official Hansard transcripts. The Internet address is: http://www.aph.gov.au/hansard To search the parliamentary database, go to: http://search.aph.gov.au HOUSE OF REPRESENTATIVES SELECT COMMITTEE ON THE RECENT AUSTRALIAN BUSHFIRES Thursday, 10 July 2003 Members: Mr Nairn (Chair), Mr Adams (Deputy Chair), Mr Bartlett, Mr Causley, Ms Ellis, Mrs Gash, Mr Gibbons, Mr Hawker, Mr McArthur, Mr Mossfield, Mr O’Connor, Mr Organ, Ms Panopoulos and Mr Schultz. Members in attendance: Mr Bartlett, Mr McArthur, Mr Nairn, Mr Organ, Ms Panopoulos and Mr Schultz. Terms of reference for the inquiry: The Select Committee on the recent Australian Bushfires seeks to identify measures that can be implemented by governments, industry and the community to minimise the incidence of, and impact of bushfires on, life, property and the environment with specific regard to the following. (a) the extent and impact of the bushfires on the environment, private and public assets and local communities; (b) the causes of and risk factors contributing