Analytical Models Correlation for Vehicle Dynamic Handling Properties
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Automotive Service Modern Auto Tech Study Guide Chapter 67 & 69 Pages 1280 1346 Suspension & Steering 32 Points Automotive Service 1
Automotive Service Modern Auto Tech Study Guide Chapter 67 & 69 Pages 1280 1346 Suspension & Steering 32 Points Automotive Service 1. The ____________________ system allows a vehicle’s tires & wheels to move up and down as they roll. Steering Suspension Brake Automotive Service 2. Suspension can be grouped into 2 broad categories: _________________ & ________________. Independent & Nonindependent Coil Springs & Air Springs Active & Passive Automotive Service 3. The perfect suspension system balances understeer and oversteer, resulting in ______________ steering. Tight Neutral Loose Automotive Service 4. Compressing springs is known as ________. As springs extend, they are said to ________. Jounce, Rebound Bounce, Resound Dribble, Rebound Automotive Service 5. Springs can be one of 4 types: A. _________, B. __________, C. _________________ ______, & D. _______. Coil Leaf Air Torsion Bar Automotive Service 6. ______________ weight is all of the weight supported by the springs. __________________ weight is all of the weight not supported by the springs. The more sprung weight, the better the vehicle will ride. Spring, Unspring Sprang, Unsprang Sprung, Unsprung Automotive Service 7. Control arms are connected to the steering knuckles with pivoting joints called ___________ joints. Automotive Service Automotive Service 8. __________ ______________ limit spring oscillations (jounce & rebound), but don’t effect ride height Slack Absorbers Shock Absorbers Shock Restorers Automotive Service 9. ______ shocks are filled with low pressure nitrogen gas to prevent fluid aeration (bubble formation). Gas Water Air Automotive Service 10. Options on shock absorbers include the ___________________________ feature & adjustable stiffness. SelfLeveling SelfIgniting SelfEnergizing Automotive Service Automotive Service Automotive Service 11. A ______ assembly consists of a shock, coil spring & an upper damper/pivot bearing. -

Driving Near the Limits Dick Maybach, Appalachian Region – PCA [email protected] January 13, 2018
Driving Near the Limits Dick Maybach, Appalachian Region – PCA [email protected] January 13, 2018 This work is licensed under the Creative Commons Attribution-noncommercial 4.0 International License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc/4.0/ or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042, USA. You are free to: • Share – copy and redistribute the material in any medium or format • Adapt – remix, transform, and build upon the material • The licensor cannot revoke these freedoms as long as you follow the license terms. Under the following terms: • Attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use. • NonCommercial – You may not use the material for commercial purposes. • No additional restrictions – You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits. This article has two main topics, vehicle dynamics and driving techniques, and concludes with a brief recap. We’ll begin vehicle dynamics by looking at a single tire, because all forces, whether you’re accelerating, braking, or turning, are applied through your tires. Next we’ll look at understeer and oversteer. Understanding these key concepts is essential to maintain control of your car as you maneuver. Another important aspect of vehicle dynamics is weight shifting. As your car changes speed and direction, the distribution of traction among your tires also changes. -

Car Suspension and Handling Fourth Edition
Car Suspension and Handling Fourth Edition List of Chapters: Preface to the Fourth Edition 3.8 Tire Uniformity 3.9 Aspect Ratios Preface to the First Edition 3.10 Tire Selection and Air Chamber Geometry Notation 3.11 References Chapter 1 Introduction Chapter 4 Steering 1.1 Scope and Layout of the Book 4.1 Dynamic Function of the Steering 1.2 The Function of the Suspension System System 4.2 Steering Angles: Effects of Tire Slip 1.3 Suspension Geometry Angles and Steering and Suspension 1.4 Kinematics and Compliance (K&C) Kinematics 1.5 Vehicle Dynamics 4.3 Relative Positions of Front- and Rear- 1.6 References Wheel Tracks 4.4 Understeer and Oversteer Chapter 2 Disturbances and Sensitivity 4.5 Directional Stability 2.1 Road Irregularities 4.6 Torque in the Steering System 2.2 Influence of Wheel Size 4.7 Steering Torque Effects Due to 2.3 Subjective Assessment of Ride Steering Geometry 2.4 Human Sensitivity to Vibration 4.8 The Steering Column 2.5 Measurement Standards for Vibration 4.9 Steering Gear 2.6 Influence of Noise on Assessment of 4.10 Constant Velocity (CV) Driveshaft Ride Comfort Joints 2.7 Influence of Phase of Differential 4.11 Torque Steer Effects Vibration on Assessment of Ride 4.12 Front-Wheel Steering Oscillations— Comfort Shimmy 2.8 References 4.13 Power Assistance 4.14 Electric Power Steering Chapter 3 The Wheel and Tire 4.15 Rear-Wheel Steering Systems 3.1 Introduction 4.16 References 3.2 The Wheel Rim 3.3 Tire Size Designation Chapter 5 Suspension Systems and 3.4 Tire Construction Types Their Effects 3.5 Tire Properties -

SUSP-15, Suspension Information and Upgrades Introduction The
SUSP-15, Suspension Information and Upgrades Introduction The intent of this article is to provide a discussion regarding suspension dynamics in general and information regarding potential upgrades to the 944 suspension. Suspension Dynamics To optimize the performance of your car's suspension it's essential to have an understanding of suspension dynamics. This includes and understanding of the concepts of "oversteer" and "understeer" and what must be done to correct these conditions when necessary. Now, I'm sure many of you know what oversteer and understeer are, but you may not have a complete understanding of what causes these conditions. Still others may have no idea what understeer and oversteer are. So, we'll start by discussing some suspension basics and work our way on from there. If you follow any type of auto racing, you may have overheard conversations between the driver and pit crew where the driver tells the crew that the car is "pushing" or the car is "loose". There are actually referring to understeer (push) and oversteer (loose) conditions. During hard cornering the weight of the car shifts away from the inside wheels toward the outside wheels. The softer the suspension, the more weight is transferred to the outside wheels. The added weight on the outside wheels causes the outside tires to grip better allowing the car to steer safely through the turn. With a perfectly "neutral" suspension setup, the weight would transfer such that the front and rear tires would have the same amount of grip and, at the limit, both tires would lose traction at the same time. -

36050 Federal Register / Vol
36050 Federal Register / Vol. 80, No. 120 / Tuesday, June 23, 2015 / Rules and Regulations DEPARTMENT OF TRANSPORTATION Avoidance Standards, by telephone at A. Outriggers (202) 366–9146, and by fax at (202) 493– B. Automated Steering Machine National Highway Traffic Safety 2990. For legal issues, you may contact C. Anti-Jackknife System Administration David Jasinski, Office of the Chief D. Control Trailer E. Sensors Counsel, by telephone at (202) 366– F. Ambient Conditions 49 CFR Part 571 2992, and by fax at (202) 366–3820. You G. Road Test Surface [Docket No. NHTSA–2015–0056] may send mail to both of these officials H. Vehicle Test Weight at the National Highway Traffic Safety I. Tires RIN 2127–AK97 Administration, 1200 New Jersey J. Mass Estimation Drive Cycle Avenue SE., Washington, DC 20590. K. Brake Conditioning Federal Motor Vehicle Safety SUPPLEMENTARY INFORMATION: L. Compliance Options Standards; Electronic Stability Control M. Data Collection Systems for Heavy Vehicles Table of Contents XII. ESC Disablement I. Executive Summary A. Summary of Comments AGENCY: National Highway Traffic II. Statutory Authority B. Response to Comments Safety Administration (NHTSA), III. Background XIII. ESC Malfunction Detection, Telltale, Department of Transportation (DOT). IV. Safety Need and Activation Indicator ACTION: Final rule. A. Heavy Vehicle Crash Problem A. ESC Malfunction Detection B. Contributing Factors in Rollover and B. ESC Malfunction Telltale SUMMARY: This document establishes a Loss-of-Control Crashes C. Combining ESC Malfunction Telltale new Federal Motor Vehicle Safety C. NTSB Safety Recommendations With Related Systems Standard No. 136 to require electronic D. Motorcoach Safety Plan D. ESC Activation Indicator stability control (ESC) systems on truck E. -

IFS on Trucks Will Explained in Chapter 3
Independent Front Suspension on Trucks Ride comfort analysis and improvements Ing. P.W. Fleuren DCT Report no: 2009.065 TU/e Master’s Thesis Supervisor: Prof. Dr. H. Nijmeijer (Eindhoven University of Technology) Coach: Dr. Ir. I.J.M. Besselink (Eindhoven University of Technology) Committee: Dr. Ir. F.E. Veldpaus (Eindhoven University of Technology) Ir. R. Liebregts (DAF Trucks) Eindhoven University of Technology Department of Mechanical Engineering Dynamics and Control group Eindhoven, January 2009 Prefaceii 8.4 Ride comfort weighting functions iii Preface Over the past year I have been working on my master’s thesis. It started with answering a question coming from the truck market. Answering this question resulted in many more questions, which take most of the time of my master project to answer them. At the end of my master project I have researched and developed some goals to deal with the most important problem. In the beginning of my master project I had intensive contact with different people form the truck industry, who submitted the question. To answer this question I moved in to the automotive engineering science laboratory which is located within the mechanical engineering facility of the TU/e. Here I had the most important tools like the, the tractor semi-trailer multi-body model to my disposal. In the mean time I remained in contact with the truck market, while answering their questions. I was working with different people which all had there own view on the problem. During this master project I learned to search for an answer using multi-body theory in a multi-body simulation model. -
Test #2 11/6/09 Closed Book, Closed Notes
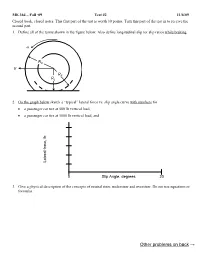
ME 364 – Fall ‘09 Test #2 11/6/09 Closed book, closed notes. This first part of the test is worth 30 points. Turn this part of the test in to receive the second part. 1. Define all of the terms shown in the figure below. Also define longitudinal slip (or slip ratio) while braking. RU V RE RL 2. On the graph below sketch a “typical” lateral force vs. slip angle curve with numbers for a passenger car tire at 500 lb vertical load, a passenger car tire at 1000 lb vertical load, and Lateral force, lb 0 Slip Angle, degrees 20 3. Give a physical description of the concepts of neutral steer, understeer and oversteer. Do not use equations or formulas. Other problems on back → 4. Define the following terminology related to vehicle dynamics: Ackerman steer angle roll center sideslip angle tire scrub Other problems on back → ME 364 – Fall ‘09 Test #2 11/6/09 Closed book, closed notes, one 8.5 x 11 inch page of handwritten formulas allowed. Show all work. 5. Weight and geometric data 700 Vertical Load for a vehicle is given below. 2000 lb Experimental data for the 1800 lb tires used on this vehicle is 600 1600 lb shown in the plot. Determine: 500 1400 lb a) Cornering stiffness of a front tire 1200 lb 400 b) Cornering stiffness of a 1000 lb rear tire 800 lb 300 c) Understeer gradient 600 lb 200 d) Steer angle required for . Fy Force, (lb) Lateral this vehicle to travel a circle of radius 100 R=240 feet at a speed of 60 mph 0 0 0.5 1 1.5 2 Slip Angle, a (deg) Curb Weight: 4370 lb Inches Feet Wheelbase: 116.0 9.67 CG distance behind front axle: 51.04 4.25 CG distance in front of rear axle: 64.96 5.42 CG distance from ground: 23.28 1.94 6. -

The Synaptic Damping Control System: Increasing the Drivers Feeling and Perception by Means of Controlled Dampers
The Synaptic Damping Control System: increasing the drivers feeling and perception by means of controlled dampers Giordano Greco Magneti Marelli SDC Vehicle control strategies Stuttgart, 6 May 2008 From ‘passive’ to ‘controlled’ suspension Vehicle suspension systems should guarantee: Safety & Comfort handling Passive suspension Comfort vehicle Sport Vehicle Suspension tuning Soft suspension Rigid suspension Low damping suspension High damping suspension Controlled suspension Adapt its behavior to different running conditions and to driver requests Stuttgart, 6 May 2008 2 The Synaptic Damping Control system Synaptic Damping Control (SDC) is the continuous damping system by Magneti Marelli suited to control vertical vehicle dynamics and body motions, caused by road surface and by driver inputs (steering wheel, accelerator, brake, gears,..), through controlled shock absorbers. The system is made up of the following components: 4 Electronically controlled shock Command current increases absorbers 400 300 1 Electronic Control Unit (ECU) 200 100 ) daN 3 Body Accelerometers ( Force 0 0 100 200 300 400 500 600 700 800 900 1000 2 Front Hub Accelerometers -100 -200 Embedded SW Control strategies -300 Velocity (mm/s) CAN node connection Command current increases Electronically controlled shock absorbers include proportional electro-valves which continuously vary their characteristics from a minimum (low command current) to a maximum (high command current) damping curve. Stuttgart, 6 May 2008 3 The Synaptic Damping Control system architecture Front left body accelerometer Front right body accelerometer Rear left body accelerometer Front left hub accelerometer Front right hub accelerometer Rear Sensors set ECU shock absorbers Front shock absorbers CAN network ¾Engine control node; ¾Gear-shift control node; CAN signals from: ¾ABS, EBD, ASR, VDC control node; ¾Steering wheel control node; ¾Body computer node. -

Ford RSC 1 ROLL RATE BASED STABILITY CONTROL
ROLL RATE BASED STABILITY CONTROL - THE ROLL STABILITY CONTROL ™ SYSTEM Jianbo Lu Dave Messih Albert Salib Ford Motor Company United States Paper Number 07-136 ABSTRACT precise detection of potential rollover conditions and driving conditions such as road bank and vehicle This paper presents the Roll Stability Control ™ loading, the aforementioned approaches need to system developed at Ford Motor Company. It is an conduct necessary trade-offs between control active safety system for passenger vehicles. It uses a sensitivity and robustness. roll rate sensor together with the information from the conventional electronic stability control hardware to In this paper, a system referred to as Roll Stability detect a vehicle's roll condition associated with a Control™ (RSC), is presented. Such a system is potential rollover and executes proper brake control designed specifically to mitigate vehicular rollovers. and engine torque reduction in response to the The idea of RSC, first documented in [10], was detected roll condition so as to mitigate a vehicular developed at Ford Motor Company and has been rollover. implemented on various vehicles within Ford Motor Company since its debut on the 2003 Volvo XC90. INTRODUCTION The RSC system adds a roll rate sensor and necessary control algorithms to an existing ESC system. The The traditional electronic stability control (ESC) roll rate sensor, together with the information from systems aim to control the yaw and sideslip angle of a the ESC system, help to effectively identify the moving vehicle through individual wheel braking and critical roll conditions which could lead to a potential engine torque reduction such that the desired path of vehicular rollover. -

Car Control and Driver Training Manual
CAR CONTROL AND DRIVER TRAINING MANUAL TABLE OF CONTENTS: PAGE TITLE ii WELCOME 1 SEATING POSITION SAFETY HARNESS 2 STEERING WHEEL/HAND POSITION SHIFTING 3 THE FOUR CONTACT PATCHES 4 HEEL & TOE TECHNIQUE 5 ORDER OF EVENTS 6 GENERAL INFORMATION 7 OUT ON THE COURSE 8 CORNERING 9 PROPER ENTRY, APEX AND EXIT OF CORNER 10 HOW TO WORK A CORNER PROPERLY 11 HOW TO WORK A CORNER PROPERLY (90°) 12 TRAILING BRAKE TECHNIQUE 13 UNDERSTEER 14 OVERSTEER 15 CAUSE AND CORRECTION 16 PASSING PROCEDURES IF YOU GO OFF COURSE 17 BE PREPARED 18 GLOSSARY 22 FLAGS AND THEIR MEANING 23 NOTES WELCOME TO THE PORSCHE OWNERS CLUB! Judging by the car you have chosen, you are a driver of a special breed, and you are probably no novice when it comes to automobiles. Remember, however, that, as with any vehicle, you should take time to familiarize yourself with your PORSCHE and its performance characteristics. Our objective is to instruct you in the basic techniques of car control. This manual along with proper instruction should answer why certain things occur under certain conditions and give you an understanding of the proper procedures to use in order to maintain control of your vehicle. You are about to learn a great deal about car control and yourself. MOST OF ALL, HAVE FUN, AND GOOD LUCK! ii SEATING POSITION: BE COMFORTABLE! Your seat position should be such that you can reach all the controls (i.e. steering wheel, gear shift lever, all pedals). The back of the car seat, as well as the under leg portion, should make as much contact with you as possible. -

HPDE Handbook (Rev-B 2016) 2
Introduction – This handbook is a selection of fundamentals put together to help you increase your knowledge of both car dynamics and driving at Higher Performance levels. It begins with the concept of understanding the complete driving ‘System’. A system that encompasses 5 varying elements that must all be considered and are key in further developing your skills. Included after that are detailed outlines of some of the principles, techniques, and terms that will guide you as you progress. This book is meant strictly as an aid and is in no-way a replacement for actual practice and experience. The information contained here-in should serve as a basis from which you can expand upon by attending several of our Driver’s Education events. TABLE OF CONTENTS START WITH DRIVING STYLE: A SYSTEM OF 5 ELEMENTS…………………………………… 3 FLAGS………………………………………………………………………………………………………………… 5 PROPER SEAT POSITIONING………………………………………………………………………………. 6 SMOOTHNESS AND CONSISTENCY AND CONCENTRATION………………………………… 7 UPSHIFTING AND DOWNSHIFTING……………………………………………………………………. 7 OVERSTEER AND UNDERSTEER…………………………………………………………………………. 8 TRAILBRAKING TECHNIQUE .………………………………………………………………………….…. 9 THE LINE…………………………………………………………………………………………………………... 10 GUIDELINE OF LEARNING ASPECTS IN DIFFERENT RUN GROUPS………………………. 12 TRACK MAP………………………………………………………………………………………………………. 13 TERMS…………………………………………………………………………………………………………….….14 SEM PCA – HPDE Handbook (rev-B 2016) 2 Start with Driving Style: A System of 5 Elements 1: The first element - The human being: Why you first? Because you are the driver. Because in the end, everything depends on yourself. You want to become a better driver, you want to be faster, you want to be in control of the car, you want to learn (which means to accept criticism and feedback, discipline and endurance) — you want to win! You are the most variable Element of the whole System. -

Analysis and Testing of the Steady-State Turning Of
Pages 135-161 ANALYSIS AND TESTING OF THE STEADY-STATE TURNING OF MULTIAXLE TRUCKS Christopher Winkler University of Michigan Transportation Research Institute John Aurell Volvo Truck Corporation ABSTRACT The International Standards Organization (ISO) is currently involved in an effort to develop a standard test procedure for evaluating the steady-state turning behavior of heavy vehicles.1 In the course of developing this standard, a new analysis has evolved which expands the basic understanding of the steady-state turning of all motor vehicles. The established, simplified analyses of steady-state turning are based on a simple vehicle model in which lateral acceleration is the only motion variable that affects tire slip angles. The new analysis examines a more complex vehicle whose slip angles depend on lateral acceleration plus another motion variable. Basic differences in the steady-state turning behavior of simple and complex vehicles are explained using the handling diagram. It is shown that the complex vehicle can be represented as a simple vehicle with an equivalent wheelbase. Trucks with multiple, nonsteering rear axles are one example of the complex vehicle. An analysis specific to such trucks is presented as is a physical interpretation of the equivalent wheelbase of trucks. Results from simulated and actual track tests which confirm this analysis are presented. INTRODUCTION The steady-state handling performance of the pneumatic-tired vehicle has been well understood for some time. While many papers on the subject appear in the literature, Pacejka presented an excellent review of the state-of-the-art understanding in a series of three papers in 1973 [1,2,3] 2 The more germane points of these papers are reviewed herein, but the reader is urged to become familiar with these papers before proceeding.