DOCSLIB.ORG

A Rational Expression Is an Expression Which Is the Ratio of Two Polynomials: Example of Rational Expressions: 2X

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Rational Expression Is an Expression Which Is the Ratio of Two Polynomials: Example of Rational Expressions: 2X A Rational Expression is an expression which is the ratio of two polynomials: Example of rational expressions: 2x − 1 1 x3 + 2x − 1 5x2 − 2x + 1 , − , , = 5x2 − 2x + 1 3x2 + 4x − 1 x2 + 1 3x + 2 1 Notice that every polynomial is a rational expression with denominator equal to 1. x2 + 5 For example, x2 + 5 = 1 Think of the relationship between rational expression and polynomial as that be- tween rational numbers and integers. The domain of a rational expression is all real numbers except where the denomi- nator is 0 3x + 4 Example: Find the domain of x2 + 3x − 4 Ans: x2 + 3x − 4 = 0 ) (x + 4)(x − 1) = 0 ) x = −4 or x = 1 Since the denominator, x2 + 3x − 4, of this rational expression is equal to 0 when x = −4 or x = 1, the domain of this rational expression is all real numbers except −4 or 1. In general, to find the domain of a rational expression, set the denominator equal to 0 and solve the equation. The domain of the rational expression is all real numbers except the solution. To Multiply rational expressions, multiply the numerator with the numerator, and multiply denominator with denominator. Cross cancell if possible. Example: x2 + 3x + 2 x2 − 2x + 1 (x + 1)(x + 2) (x − 1)(x − 1) x − 1 · = · = x2 − 1 x2 + 5x + 6 (x − 1)(x + 1) (x + 2)(x + 3) x + 3 To Divide rational expressions, flip the divisor and turn into a multiplication. Example: x2 − 2x + 1 x2 − 1 x2 − 2x + 1 x2 − 16 (x − 1)(x − 1) (x + 4)(x − 4) ÷ = · = · x2 + 5x + 4 x2 − 16 x2 + 5x + 4 x2 − 1 (x + 4)(x + 1) (x + 1)(x − 1) (x − 1) (x − 4) x2 − 5x + 4 = · = (x + 1) (x + 1) x2 + 2x + 1 To Add or Subtract rational expressions, we need to find common denominator by finding the Least Common Multiple, or LCM of the denominators. Example: x + 1 1 + x − 1 x2 − 1 Ans: We can factor the denominator of the second fraction: x + 1 1 x + 1 1 + = + x − 1 x2 − 1 x − 1 (x − 1)(x + 1) The LCM of the two fractions is (x − 1)(x + 1) since these are the two factors that are present in one or the other fraction. To obtain commond denominator, we need to multiply the numerator and denominator of the first fraction by x + 1: x + 1 1 (x + 1)(x + 1) 1 + = + x − 1 (x − 1)(x + 1) (x − 1)(x + 1) (x − 1)(x + 1) x2 + 2x + 1 1 (x2 + 2x + 1) + 1 x2 + 2x + 2 = + = = x2 − 1 x2 − 1 x2 − 1 x2 − 1 Example: 2x − 3 x + 7 2x − 3 x + 7 − = − x2 + 3x + 2 x2 − x − 6 (x + 2)(x + 1) (x + 2)(x − 3) The L.C.M of the two fractions is (x + 2)(x + 1)(x − 3). We have: 2x − 3 x + 7 (2x − 3)(x − 3) (x + 7)(x + 1) − = − (x + 2)(x + 1) (x + 2)(x − 3) (x + 2)(x + 1)(x − 3) (x + 2)(x − 3)(x + 1) 2x2 − 9x + 9 x2 + 8x + 7 (2x2 − 9x + 9) − (x2 + 8x + 7) = − = (x + 2)(x + 1)(x − 3) (x + 2)(x − 3)(x + 1) (x + 2)(x − 3)(x + 1) 2x2 − 9x + 9 − x2 − 8x − 7 x2 − 17x + 2 = = (x + 2)(x − 3)(x + 1) (x + 2)(x − 3)(x + 1) To perform Long Division of Polynomials, we use a process similar to long division of integers. If we were to divide two numbers, say 2137 ÷ 13, we start by writing the dividen, 2137, inside the division sign, and the divisor, 13, outside. We proceed by finding out how many times the divisor, 13, goes into the dividend/remainder: 164 13 2137 1300 837 780 57 52 5 We do long division of polynomial similarly. We put the dividend inside the division symbol and the divisor on the outside, and proceed similar to that of long division of numbers. Example: Divide the polynomial x3 + 3x2 − 3x + 4 by the polynomail x − 4. In other words, we want (x3 + 3x2 − 3x + 4) ÷ (x − 4) Ans: We first put the dividend, x3 +3x2 −3x+4 inside of the long division symbol, and the divisor, x − 4, outside: x − 4 x3 + 3x2 − 3x + 4 We ask, what multiplied to x will give x3 ? Answer is x2, so we put x2 on the first column on top of the long division symbol. Note that the powers of the x’s should line-up. x2 x − 4 x3 + 3x2 − 3x + 4 We now multiply x2 to the divisor, x−4, and subtract this result from the dividend. x2 x − 4 x3 + 3x2 − 3x + 4 − x3 + 4x2 We get a new polynomial with a lower degree. We repeat the process with this polynomial. x2 x − 4 x3 + 3x2 − 3x + 4 − x3 + 4x2 7x2 − 3x What multiplied to x will give 7x2 ? Answer is 7x, so we put 7x in the next column on top. x2 + 7x x − 4 x3 + 3x2 − 3x + 4 − x3 + 4x2 7x2 − 3x We then repeat the process, multiply 7x to the divisor, x − 4, and subtract the result from the top: x2 + 7x x − 4 x3 + 3x2 − 3x + 4 − x3 + 4x2 7x2 − 3x − 7x2 + 28x We get yet another expression of lower degree. x2 + 7x x − 4 x3 + 3x2 − 3x + 4 − x3 + 4x2 7x2 − 3x − 7x2 + 28x 25x + 4 We repeat the process until the degree of the remainder is strictly less than the degree of the divisor. At this stage, the degree of the remainder, 25x + 4, is 1, which is equal to the degree of the divisor, x − 4, we must still continue. We ask, what multiplied to x will give 25x? Answer is 25, so we put 25 on top: x2 + 7x + 25 x − 4 x3 + 3x2 − 3x + 4 − x3 + 4x2 7x2 − 3x − 7x2 + 28x 25x + 4 Multiply 25 to x − 4 and subtract the result from the top: x2 + 7x + 25 x − 4 x3 + 3x2 − 3x + 4 − x3 + 4x2 7x2 − 3x − 7x2 + 28x 25x + 4 − 25x + 100 The remainder is now the constant 104. The degree of a constant is 0, which is strictly less than the degree of the divisor. We are done. x2 + 7x + 25 x − 4 x3 + 3x2 − 3x + 4 − x3 + 4x2 7x2 − 3x − 7x2 + 28x 25x + 4 − 25x + 100 104 In this completed long division, the quotient is the polynomial x2 + 7x + 25, the remainder is the polynomial 104. Example: Perform the long division and find the quotient and remainder: (3x5 − 2x3 + 4x2 + 1) ÷ (x2 − x + 1) Ans: Notice that the dividend, (3x5 − 2x3 + 4x2 + 1), has some missing powers of x (missing x4 and x term). When performing the long division, we should leave enough space inside the long division symbol so we can align the powers of x’s correctly. Another approach to make sure that the powers of x’s are lined-up correctly is to fill in 0’s where powers of x are missing. Remember that only like powers of x’s can be subtracted or added. 3x3 + 3x2 − 2x − 1 x2 − x + 1 3x5 − 2x3 + 4x2 + 1 − 3x5 + 3x4 − 3x3 3x4 − 5x3 + 4x2 − 3x4 + 3x3 − 3x2 − 2x3 + x2 2x3 − 2x2 + 2x − x2 + 2x + 1 x2 − x + 1 x + 2 The quotient polynomial is 3x3 + 3x2 − 2x − 1. The remainder polynomial is x + 2. Example: Perform the long division and find the quotient and remainder: (2x4 − x2 − 3x) ÷ (x2 − 1) This time, both the dividend and divisor have missing powers of x. Pay close attention to spacing and alignment when trying to subtract the polynomials from each other: 2x2 + 1 x2 − 1 2x4 − x2 − 3x − 2x4 + 2x2 x2 − 3x − x2 + 1 − 3x + 1 The quotient is 2x2 + 1, remainder is −3x + 1. Example: Perform the long division to find quotient and remainder: (x5 − 4x3 + x2 − 3x + 2) ÷ (x − 2) Ans: x4 + 2x3 + x − 1 x − 2 x5 − 4x3 + x2 − 3x + 2 − x5 + 2x4 2x4 − 4x3 − 2x4 + 4x3 x2 − 3x − x2 + 2x − x + 2 x − 2 0 In this example, when (x5 − 4x3 + x2 − 3x + 2) is divided by (x − 2), the remainder is 0. We say that (x − 2) is a factor of (x5 − 4x3 + x2 − 3x + 2). To solve Rational Expression Equations, multiply both sides of the equation by the LCM of the frations to eliminate the fraction. Be sure to check for Extraneous Solution. E.g. 18 2 + = 4 y + 1 5 The LCM of the fractions is 5(y + 1), so we multiply both sides of the equation by 5(y + 1). 18 2 5(y + 1) + = [5(y + 1)]4 y + 1 5 18 2 5(y + 1) + 5(y + 1) = 20(y + 1) y + 1 5 5 · 18 + 2(y + 1) = 20y + 20 90 + 2y + 2 = 20y + 20 2y + 92 = 20y + 20 18y = 72 y = 4 Any time we multiplied both sides of the equation by a variable term, we could potentially have introduced extraneous solution, which are numbers that shows up in the process of solving an equation when we perform some operations (like multiply both sides by a variable term or square both sides). An extraneous solution is not a solution to an equation. Notice the difference between an extraneous solution from a wrong solution, which is a number that simply comes from something you did incorrectly. You could have made no algebraic or other mathematical error and you could still introduce extra- neous solution. Extraneous solution comes from the result of some mathematical process of solving an equation, such as multiply both sides by a variable term or square both sides.
Load more

Recommended publications
  • Black Hills State University
    Black Hills State University MATH 341 Concepts addressed: Mathematics Number sense and numeration: meaning and use of numbers; the standard algorithms of the four basic operations; appropriate computation strategies and reasonableness of results; methods of mathematical investigation; number patterns; place value; equivalence; factors and multiples; ratio, proportion, percent; representations; calculator strategies; and number lines Students will be able to demonstrate proficiency in utilizing the traditional algorithms for the four basic operations and to analyze non-traditional student-generated algorithms to perform these calculations. Students will be able to use non-decimal bases and a variety of numeration systems, such as Mayan, Roman, etc, to perform routine calculations. Students will be able to identify prime and composite numbers, compute the prime factorization of a composite number, determine whether a given number is prime or composite, and classify the counting numbers from 1 to 200 into prime or composite using the Sieve of Eratosthenes. A prime number is a number with exactly two factors. For example, 13 is a prime number because its only factors are 1 and itself. A composite number has more than two factors. For example, the number 6 is composite because its factors are 1,2,3, and 6. To determine if a larger number is prime, try all prime numbers less than the square root of the number. If any of those primes divide the original number, then the number is prime; otherwise, the number is composite. The number 1 is neither prime nor composite. It is not prime because it does not have two factors. It is not composite because, otherwise, it would nullify the Fundamental Theorem of Arithmetic, which states that every composite number has a unique prime factorization.
    [Show full text]
  • Saxon Course 1 Reteachings Lessons 21-30
    Name Reteaching 21 Math Course 1, Lesson 21 • Divisibility Last-Digit Tests Inspect the last digit of the number. A number is divisible by . 2 if the last digit is even. 5 if the last digit is 0 or 5. 10 if the last digit is 0. Sum-of-Digits Tests Add the digits of the number and inspect the total. A number is divisible by . 3 if the sum of the digits is divisible by 3. 9 if the sum of the digits is divisible by 9. Practice: 1. Which of these numbers is divisible by 2? A. 2612 B. 1541 C. 4263 2. Which of these numbers is divisible by 5? A. 1399 B. 1395 C. 1392 3. Which of these numbers is divisible by 3? A. 3456 B. 5678 C. 9124 4. Which of these numbers is divisible by 9? A. 6754 B. 8124 C. 7938 Saxon Math Course 1 © Harcourt Achieve Inc. and Stephen Hake. All rights reserved. 23 Name Reteaching 22 Math Course 1, Lesson 22 • “Equal Groups” Word Problems with Fractions What number is __3 of 12? 4 Example: 1. Divide the total by the denominator (bottom number). 12 ÷ 4 = 3 __1 of 12 is 3. 4 2. Multiply your answer by the numerator (top number). 3 × 3 = 9 So, __3 of 12 is 9. 4 Practice: 1. If __1 of the 18 eggs were cracked, how many were not cracked? 3 2. What number is __2 of 15? 3 3. What number is __3 of 72? 8 4. How much is __5 of two dozen? 6 5.
    [Show full text]
  • RATIO and PERCENT Grade Level: Fifth Grade Written By: Susan Pope, Bean Elementary, Lubbock, TX Length of Unit: Two/Three Weeks
    RATIO AND PERCENT Grade Level: Fifth Grade Written by: Susan Pope, Bean Elementary, Lubbock, TX Length of Unit: Two/Three Weeks I. ABSTRACT A. This unit introduces the relationships in ratios and percentages as found in the Fifth Grade section of the Core Knowledge Sequence. This study will include the relationship between percentages to fractions and decimals. Finally, this study will include finding averages and compiling data into various graphs. II. OVERVIEW A. Concept Objectives for this unit: 1. Students will understand and apply basic and advanced properties of the concept of ratios and percents. 2. Students will understand the general nature and uses of mathematics. B. Content from the Core Knowledge Sequence: 1. Ratio and Percent a. Ratio (p. 123) • determine and express simple ratios, • use ratio to create a simple scale drawing. • Ratio and rate: solve problems on speed as a ratio, using formula S = D/T (or D = R x T). b. Percent (p. 123) • recognize the percent sign (%) and understand percent as “per hundred” • express equivalences between fractions, decimals, and percents, and know common equivalences: 1/10 = 10% ¼ = 25% ½ = 50% ¾ = 75% find the given percent of a number. C. Skill Objectives 1. Mathematics a. Compare two fractional quantities in problem-solving situations using a variety of methods, including common denominators b. Use models to relate decimals to fractions that name tenths, hundredths, and thousandths c. Use fractions to describe the results of an experiment d. Use experimental results to make predictions e. Use table of related number pairs to make predictions f. Graph a given set of data using an appropriate graphical representation such as a picture or line g.
    [Show full text]
  • Random Denominators and the Analysis of Ratio Data
    Environmental and Ecological Statistics 11, 55-71, 2004 Corrected version of manuscript, prepared by the authors. Random denominators and the analysis of ratio data MARTIN LIERMANN,1* ASHLEY STEEL, 1 MICHAEL ROSING2 and PETER GUTTORP3 1Watershed Program, NW Fisheries Science Center, 2725 Montlake Blvd. East, Seattle, WA 98112 E-mail: [email protected] 2Greenland Institute of Natural Resources 3National Research Center for Statistics and the Environment, Box 354323, University of Washington, Seattle, WA 98195 Ratio data, observations in which one random value is divided by another random value, present unique analytical challenges. The best statistical technique varies depending on the unit on which the inference is based. We present three environmental case studies where ratios are used to compare two groups, and we provide three parametric models from which to simulate ratio data. The models describe situations in which (1) the numerator variance and mean are proportional to the denominator, (2) the numerator mean is proportional to the denominator but its variance is proportional to a quadratic function of the denominator and (3) the numerator and denominator are independent. We compared standard approaches for drawing inference about differences between two distributions of ratios: t-tests, t-tests with transformations, permutation tests, the Wilcoxon rank test, and ANCOVA-based tests. Comparisons between tests were based both on achieving the specified alpha-level and on statistical power. The tests performed comparably with a few notable exceptions. We developed simple guidelines for choosing a test based on the unit of inference and relationship between the numerator and denominator. Keywords: ANCOVA, catch per-unit effort, fish density, indices, per-capita, per-unit, randomization tests, t-tests, waste composition 1352-8505 © 2004 Kluwer Academic Publishers 1.
    [Show full text]
  • 7-1 RATIONALS - Ratio & Proportion MATH 210 F8
    7-1 RATIONALS - Ratio & Proportion MATH 210 F8 If quantity "a" of item x and "b" of item y are related (so there is some reason to compare the numbers), we say the RATIO of x to y is "a to b", written "a:b" or a/b. Ex 1 If a classroom of 21 students has 3 computers for student use, we say the ratio of students to computers is . We also say the ratio of computers to students is 3:21. The ratio, being defined as a fraction, may be reduced. In this case, we can also say there is a 1:7 ratio of computers to students (or a 7:1 ratio of students to computers). We might also say "there is one computer per seven students" . Ex 2 We express gasoline consumption by a car as a ratio: If w e traveled 372 miles since the last fill-up, and needed 12 gallons to fill the tank, we'd say we're getting mpg (miles per gallon— mi/gal). We also express speed as a ratio— distance traveled to time elapsed... Caution: Saying “ the ratio of x to y is a:b” does not mean that x constitutes a/b of the whole; in fact x constitutes a/(a+ b) of the whole of x and y together. For instance if the ratio of boys to girls in a certain class is 2:3, boys do not comprise 2/3 of the class, but rather ! A PROPORTION is an equality of tw o ratios. E.x 3 If our car travels 500 miles on 15 gallons of gas, how many gallons are needed to travel 1200 miles? We believe the fuel consumption we have experienced is the most likely predictor of fuel use on the trip.
    [Show full text]
  • Measurement & Transformations
    Chapter 3 Measurement & Transformations 3.1 Measurement Scales: Traditional Classifica- tion Statisticians call an attribute on which observations differ a variable. The type of unit on which a variable is measured is called a scale.Traditionally,statisticians talk of four types of measurement scales: (1) nominal,(2)ordinal,(3)interval, and (4) ratio. 3.1.1 Nominal Scales The word nominal is derived from nomen,theLatinwordforname.Nominal scales merely name differences and are used most often for qualitative variables in which observations are classified into discrete groups. The key attribute for anominalscaleisthatthereisnoinherentquantitativedifferenceamongthe categories. Sex, religion, and race are three classic nominal scales used in the behavioral sciences. Taxonomic categories (rodent, primate, canine) are nomi- nal scales in biology. Variables on a nominal scale are often called categorical variables. For the neuroscientist, the best criterion for determining whether a variable is on a nominal scale is the “plotting” criteria. If you plot a bar chart of, say, means for the groups and order the groups in any way possible without making the graph “stupid,” then the variable is nominal or categorical. For example, were the variable strains of mice, then the order of the means is not material. Hence, “strain” is nominal or categorical. On the other hand, if the groups were 0 mgs, 10mgs, and 15 mgs of active drug, then having a bar chart with 15 mgs first, then 0 mgs, and finally 10 mgs is stupid. Here “milligrams of drug” is not anominalorcategoricalvariable. 1 CHAPTER 3. MEASUREMENT & TRANSFORMATIONS 2 3.1.2 Ordinal Scales Ordinal scales rank-order observations.
    [Show full text]
  • Proportions: a Ratio Is the Quotient of Two Numbers. for Example, 2 3 Is A
    Proportions: 2 A ratio is the quotient of two numbers. For example, is a ratio of 2 and 3. 3 An equality of two ratios is a proportion. For example, 3 15 = is a proportion. 7 45 If two sets of numbers (none of which is 0) are in a proportion, then we say that the numbers are proportional. a c Example, if = , then a and b are proportional to c and d. b d a c Remember from algebra that, if = , then ad = bc. b d The following proportions are equivalent: a c = b d a b = c d b d = a c c d = a b Theorem: Three or more parallel lines divide trasversals into proportion. l a c m b d n In the picture above, lines l, m, and n are parallel to each other. This means that they divide the two transversals into proportion. In other words, a c = b d a b = c d b d = a c c d = a b Theorem: In any triangle, a line that is paralle to one of the sides divides the other two sides in a proportion. E a c F G b d A B In picture above, FG is parallel to AB, so it divides the other two sides of 4AEB, EA and EB into proportions. In particular, a c = b d b d = a c a b = c d c d = a b Theorem: The bisector of an angle in a triangle divides the opposite side into segments that are proportional to the adjacent side.
    [Show full text]
  • A Tutorial on the Decibel This Tutorial Combines Information from Several Authors, Including Bob Devarney, W1ICW; Walter Bahnzaf, WB1ANE; and Ward Silver, NØAX
    A Tutorial on the Decibel This tutorial combines information from several authors, including Bob DeVarney, W1ICW; Walter Bahnzaf, WB1ANE; and Ward Silver, NØAX Decibels are part of many questions in the question pools for all three Amateur Radio license classes and are widely used throughout radio and electronics. This tutorial provides background information on the decibel, how to perform calculations involving decibels, and examples of how the decibel is used in Amateur Radio. The Quick Explanation • The decibel (dB) is a ratio of two power values – see the table showing how decibels are calculated. It is computed using logarithms so that very large and small ratios result in numbers that are easy to work with. • A positive decibel value indicates a ratio greater than one and a negative decibel value indicates a ratio of less than one. Zero decibels indicates a ratio of exactly one. See the table for a list of easily remembered decibel values for common ratios. • A letter following dB, such as dBm, indicates a specific reference value. See the table of commonly used reference values. • If given in dB, the gains (or losses) of a series of stages in a radio or communications system can be added together: SystemGain(dB) = Gain12 + Gain ++ Gainn • Losses are included as negative values of gain. i.e. A loss of 3 dB is written as a gain of -3 dB. Decibels – the History The need for a consistent way to compare signal strengths and how they change under various conditions is as old as telecommunications itself. The original unit of measurement was the “Mile of Standard Cable.” It was devised by the telephone companies and represented the signal loss that would occur in a mile of standard telephone cable (roughly #19 AWG copper wire) at a frequency of around 800 Hz.
    [Show full text]
  • Greatest Common Divisor and Least Common Multiple
    Greatest Common Divisor and Least Common Multiple Document #: WG21 N3845 Date: 2014-01-01 Revises: None Project: JTC1.22.32 Programming Language C++ Reply to: Walter E. Brown <[email protected]> Contents 1 Introduction ............. 1 4 Acknowledgments .......... 3 2 Implementation ........... 2 5 Bibliography ............. 4 3 Proposed wording .......... 3 6 Document history .......... 4 Abstract This paper proposes two frequently-used classical numeric algorithms, gcd and lcm, for header <cstdlib>. The former calculates the greatest common divisor of two integer values, while the latter calculates their least common multiple. Both functions are already typically provided in behind-the-scenes support of the standard library’s <ratio> and <chrono> headers. Die ganze Zahl schuf der liebe Gott, alles Übrige ist Menschenwerk. (Integers are dear God’s achievement; all else is work of mankind.) —LEOPOLD KRONECKER 1 Introduction 1.1 Greatest common divisor The greatest common divisor of two (or more) integers is also known as the greatest or highest common factor. It is defined as the largest of those positive factors1 shared by (common to) each of the given integers. When all given integers are zero, the greatest common divisor is typically not defined. Algorithms for calculating the gcd have been known since at least the time of Euclid.2 Some version of a gcd algorithm is typically taught to schoolchildren when they learn fractions. However, the algorithm has considerably wider applicability. For example, Wikipedia states that gcd “is a key element of the RSA algorithm, a public-key encryption method widely used in electronic commerce.”3 Note that the standard library’s <ratio> header already requires gcd’s use behind the scenes; see [ratio.ratio]: Copyright c 2014 by Walter E.
    [Show full text]
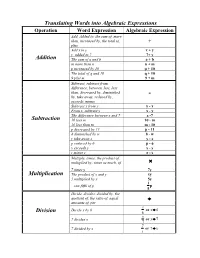
  • Translating Words Into Algebraic Expressions Addition Subtraction Multiplication Division
    Translating Words into Algebraic Expressions Operation Word Expression Algebraic Expression Add, Added to, the sum of, more than, increased by, the total of, + plus Add x to y x + y y added to 7 7+ y Addition The sum of a and b a + b m more than n n + m p increased by 10 p + 10 The total of q and 10 q + 10 9 plus m 9 + m Subtract, subtract from, difference, between, less, less than, decreased by, diminished - by, take away, reduced by, exceeds, minus Subtract x from y y - x From x, subtract y x - y The difference between x and 7 x -7 Subtraction 10 less m 10 - m 10 less than m m - 10 p decreased by 11 p - 11 8 diminished by w 8 - w y take away z y - z p reduced by 6 p - 6 x exceeds y x - y r minus s r - s Multiply, times, the product of, multiplied by, times as much, of × 7 times y 7y Multiplication The product of x and y xy 5 multiplied by y 5y 1 one-fifth of p p 5 Divide, divides, divided by, the quotient of, the ratio of, equal ÷ amounts of, per x Divide x by 6 or x ÷ 6 Division 6 x 7 divides x or x ÷ 7 7 7 7 divided by x or 7 ÷ x x y The quotient of y and 5 or y ÷ 5 5 u The ratio of u to v or u ÷ v v u Division u separated into 4 equal parts or u ÷ 4 (continued) 4 5 5 parts per 100 parts 100 The square of y y2 Power The cube of k k3 t raised to the fourth power t4 Is equal to, the same as, is, are, the result of, will be, are, yields = Equals x is equal to y x = y p is the same as q p = q Two, two times, twice, twice as Multiplication by much as, double 2 2 Twice z 2z y doubled 2y 1 Half of, one-half of, half as much as, one-half
    [Show full text]
  • Silver Ratio and Pell Numbers
    JASC: Journal of Applied Science and Computations ISSN NO: 0076-5131 Silver Ratio and Pell Numbers Dr. Vandana N. Purav P.D. Karkhanis College of Arts and Commerce, Ambarnath Email : [email protected] Abstract Like Fibonacci and Lucas Numbers, Pell and Pell-Lucas numbers are mathematical twins. From the Family of Fibonacci Numbers, Lucas Numbers were invented. This family give rise to Pell and Pell- Lucas Number. Pell and Pell-Lucas numbers have properties similar to Fibonacci and Lucas Numbers. In this note we try to focus on some of these properties of Pell Numbers related with Silver Ratio Key words : Silver Ratio , Pell Numbers, Pell-Lucas Numbers Introduction Pell numbers arise historically and most notably in the rational approximation of √2 . A sequence of Pell numbers starts with 0 and 1 and then each Pell number is the sum of twice the previous number and the Pell number before . We denote this Pell Numbers by Pn , recursively it can be written as, Pn = 2Pn-1 + Pn- 2 , n≥ 3 and P1 = 1 and P2 = 2 are the initial conditions. The Pell sequence is 1, 2, 5, 12, 29, 70, 169,….. If we change the initial conditions as P1 = 1 and P2 = 3 we get Pell-Lucas sequence, we denote it by Qn and defined recursively as Qn = 2Qn-1 + Qn-2 , n≥ 3 and Q1 = 1 and Q2 = 3, The Pell-Lucas sequence is 1, 3, 7, 17, 41, 99,…… Thus like Fibonacci and Lucas Numbers, Pell and Pell-Lucas Numbers are mathematical twins. We characterize some of the properties.
    [Show full text]
  • Measures of Model Performance Based on the Log Accuracy Ratio
    1 Measures of model performance based on the log accuracy ratio 1 1;2 3 2 S. K. Morley , T. V. Brito and D. T. Welling 1 3 Space Science and Applications, Los Alamos National Laboratory, New Mexico, 2 3 4 USA Now at: University of Helsinki, Helsinki, Finland. Climate and Space Sciences 5 and Engineering Department, University of Michigan, Michigan, USA 6 Key Points: • 7 The median symmetric accuracy and symmetric signed percentage bias are intro- 8 duced to address some drawbacks of current metrics based on relative errors • 9 The spread of a multiplicative linear model can be robustly estimated using the log 10 accuracy ratio • 11 The properties of the median symmetric accuracy and the symmetric signed per- 12 centage bias are demonstrated on radiation belt examples This is the author manuscript accepted for publication and has undergone full peer review but has not been through the copyediting, typesetting, pagination and proofreading process, which may lead to differences between this version and the Version of Record. Please cite this article as doi: 10.1002/2017SW001669 Corresponding author: S. K. Morley, [email protected] This article is protected by copyright.–1– All rights reserved. 13 Abstract 14 Quantitative assessment of modeling and forecasting of continuous quantities uses a vari- 15 ety of approaches. We review existing literature describing metrics for forecast accuracy 16 and bias, concentrating on those based on relative errors and percentage errors. Of these 17 accuracy metrics, the mean absolute percentage error (MAPE) is one of the most com- 18 mon across many fields and has been widely applied in recent space science literature and 19 we highlight the benefits and drawbacks of MAPE and proposed alternatives.
    [Show full text]