3/4-Discrete Optimal Transport
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

POWERVR 3D Application Development Recommendations
Imagination Technologies Copyright POWERVR 3D Application Development Recommendations Copyright © 2009, Imagination Technologies Ltd. All Rights Reserved. This publication contains proprietary information which is protected by copyright. The information contained in this publication is subject to change without notice and is supplied 'as is' without warranty of any kind. Imagination Technologies and the Imagination Technologies logo are trademarks or registered trademarks of Imagination Technologies Limited. All other logos, products, trademarks and registered trademarks are the property of their respective owners. Filename : POWERVR. 3D Application Development Recommendations.1.7f.External.doc Version : 1.7f External Issue (Package: POWERVR SDK 2.05.25.0804) Issue Date : 07 Jul 2009 Author : POWERVR POWERVR 1 Revision 1.7f Imagination Technologies Copyright Contents 1. Introduction .................................................................................................................................4 1. Golden Rules...............................................................................................................................5 1.1. Batching.........................................................................................................................5 1.1.1. API Overhead ................................................................................................................5 1.2. Opaque objects must be correctly flagged as opaque..................................................6 1.3. Avoid mixing -
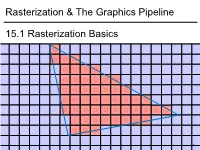
Rasterization & the Graphics Pipeline 15.1 Rasterization Basics
1 1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 15.1Rasterization Basics Rasterization & TheGraphics Pipeline Rasterization& -1 -1 -0.8 -0.6 -0.4 -0.2 0 0.2 0.4 0.6 0.8 1 In This Video • The Graphics Pipeline and how it processes triangles – Projection, rasterisation, shading, depth testing • DirectX12 and its stages 2 Modern Graphics Pipeline • Input – Geometric model • Triangle vertices, vertex normals, texture coordinates – Lighting/material model (shader) • Light source positions, colors, intensities, etc. • Texture maps, specular/diffuse coefficients, etc. – Viewpoint + projection plane – You know this, you’ve done it! • Output – Color (+depth) per pixel Colbert & Krivanek 3 The Graphics Pipeline • Project vertices to 2D (image) • Rasterize triangle: find which pixels should be lit • Compute per-pixel color • Test visibility (Z-buffer), update frame buffer color 4 The Graphics Pipeline • Project vertices to 2D (image) • Rasterize triangle: find which pixels should be lit – For each pixel, test 3 edge equations • if all pass, draw pixel • Compute per-pixel color • Test visibility (Z-buffer), update frame buffer color 5 The Graphics Pipeline • Perform projection of vertices • Rasterize triangle: find which pixels should be lit • Compute per-pixel color • Test visibility, update frame buffer color – Store minimum distance to camera for each pixel in “Z-buffer” • ~same as tmin in ray casting! – if new_z < zbuffer[x,y] zbuffer[x,y]=new_z framebuffer[x,y]=new_color frame buffer Z buffer 6 The Graphics Pipeline For each triangle transform into eye space (perform projection) setup 3 edge equations for each pixel x,y if passes all edge equations compute z if z<zbuffer[x,y] zbuffer[x,y]=z framebuffer[x,y]=shade() 7 (Simplified version) DirectX 12 Pipeline (Vulkan & Metal are highly similar) Vertex & Textures, index data etc. -

Powervr Graphics - Latest Developments and Future Plans
PowerVR Graphics - Latest Developments and Future Plans Latest Developments and Future Plans A brief introduction • Joe Davis • Lead Developer Support Engineer, PowerVR Graphics • With Imagination’s PowerVR Developer Technology team for ~6 years • PowerVR Developer Technology • SDK, tools, documentation and developer support/relations (e.g. this session ) facebook.com/imgtec @PowerVRInsider │ #idc15 2 Company overview About Imagination Multimedia, processors, communications and cloud IP Driving IP innovation with unrivalled portfolio . Recognised leader in graphics, GPU compute and video IP . #3 design IP company world-wide* Ensigma Communications PowerVR Processors Graphics & GPU Compute Processors SoC fabric PowerVR Video MIPS Processors General Processors PowerVR Vision Processors * source: Gartner facebook.com/imgtec @PowerVRInsider │ #idc15 4 About Imagination Our IP plus our partners’ know-how combine to drive and disrupt Smart WearablesGaming Security & VR/AR Advanced Automotive Wearables Retail eHealth Smart homes facebook.com/imgtec @PowerVRInsider │ #idc15 5 About Imagination Business model Licensees OEMs and ODMs Consumers facebook.com/imgtec @PowerVRInsider │ #idc15 6 About Imagination Our licensees and partners drive our business facebook.com/imgtec @PowerVRInsider │ #idc15 7 PowerVR Rogue Hardware PowerVR Rogue Recap . Tile-based deferred renderer . Building on technology proven over 5 previous generations . Formally announced at CES 2012 . USC - Universal Shading Cluster . New scalar SIMD shader core . General purpose compute is a first class citizen in the core … . … while not forgetting what makes a shader core great for graphics facebook.com/imgtec @PowerVRInsider │ #idc15 9 TBDR Tile-based . Tile-based . Split each render up into small tiles (32x32 for the most part) . Bin geometry after vertex shading into those tiles . Tile-based rasterisation and pixel shading . -

Real-Time Ray Traced Ambient Occlusion and Animation Image Quality and Performance of Hardware- Accelerated Ray Traced Ambient Occlusion
DEGREE PROJECTIN COMPUTER SCIENCE AND ENGINEERING, SECOND CYCLE, 30 CREDITS STOCKHOLM, SWEDEN 2021 Real-time Ray Traced Ambient Occlusion and Animation Image quality and performance of hardware- accelerated ray traced ambient occlusion FABIAN WALDNER KTH ROYAL INSTITUTE OF TECHNOLOGY SCHOOL OF ELECTRICAL ENGINEERING AND COMPUTER SCIENCE Real-time Ray Traced Ambient Occlusion and Animation Image quality and performance of hardware-accelerated ray traced ambient occlusion FABIAN Waldner Master’s Programme, Industrial Engineering and Management, 120 credits Date: June 2, 2021 Supervisor: Christopher Peters Examiner: Tino Weinkauf School of Electrical Engineering and Computer Science Swedish title: Strålspårad ambient ocklusion i realtid med animationer Swedish subtitle: Bildkvalité och prestanda av hårdvaruaccelererad, strålspårad ambient ocklusion © 2021 Fabian Waldner Abstract | i Abstract Recently, new hardware capabilities in GPUs has opened the possibility of ray tracing in real-time at interactive framerates. These new capabilities can be used for a range of ray tracing techniques - the focus of this thesis is on ray traced ambient occlusion (RTAO). This thesis evaluates real-time ray RTAO by comparing it with ground- truth ambient occlusion (GTAO), a state-of-the-art screen space ambient occlusion (SSAO) method. A contribution by this thesis is that the evaluation is made in scenarios that includes animated objects, both rigid-body animations and skinning animations. This approach has some advantages: it can emphasise visual artefacts that arise due to objects moving and animating. Furthermore, it makes the performance tests better approximate real-world applications such as video games and interactive visualisations. This is particularly true for RTAO, which gets more expensive as the number of objects in a scene increases and have additional costs from managing the ray tracing acceleration structures. -

Michael Doggett Department of Computer Science Lund University Overview
Graphics Architectures and OpenCL Michael Doggett Department of Computer Science Lund university Overview • Parallelism • Radeon 5870 • Tiled Graphics Architectures • Important when Memory and Bandwidth limited • Different to Tiled Rasterization! • Tessellation • OpenCL • Programming the GPU without Graphics © mmxii mcd “Only 10% of our pixels require lots of samples for soft shadows, but determining which 10% is slower than always doing the samples. ” by ID_AA_Carmack, Twitter, 111017 Parallelism • GPUs do a lot of work in parallel • Pipelining, SIMD and MIMD • What work are they doing? © mmxii mcd What’s running on 16 unifed shaders? 128 fragments in parallel 16 cores = 128 ALUs MIMD 16 simultaneous instruction streams 5 Slide courtesy Kayvon Fatahalian vertices/fragments primitives 128 [ OpenCL work items ] in parallel CUDA threads vertices primitives fragments 6 Slide courtesy Kayvon Fatahalian Unified Shader Architecture • Let’s take the ATI Radeon 5870 • From 2009 • What are the components of the modern graphics hardware pipeline? © mmxii mcd Unified Shader Architecture Grouper Rasterizer Unified shader Texture Z & Alpha FrameBuffer © mmxii mcd Unified Shader Architecture Grouper Rasterizer Unified Shader Texture Z & Alpha FrameBuffer ATI Radeon 5870 © mmxii mcd Shader Inputs Vertex Grouper Tessellator Geometry Grouper Rasterizer Unified Shader Thread Scheduler 64 KB GDS SIMD 32 KB LDS Shader Processor 5 32bit FP MulAdd Texture Sampler Texture 16 Shader Processors 256 KB GPRs 8 KB L1 Tex Cache 20 SIMD Engines Shader Export Z & Alpha 4 -

Difi: Fast Distance Field Computation Using Graphics Hardware
DiFi: Fast Distance Field Computation using Graphics Hardware Avneesh Sud Dinesh Manocha Department of Computer Science Univeristy of North Carolina Chapel Hill, NC 27599-3175 {sud,dm}@cs.unc.edu http://gamma.cs.unc.edu/DiFi Abstract Most practically efficient methods for computing the dis- tance fields in 2− or 3−space compute the distance field We present a novel algorithm for fast computation of dis- on a discrete grid. Essentially the methods fall into 2 cat- cretized distance fields using graphics hardware. Given a egories: methods based on front propagation and methods set of primitives and a distance metric, our algorithm com- based on Voronoi regions. putes the distance field along each slice of a uniform spatial Main Contributions: In this paper we present an ap- grid by rasterizing the distance functions. It uses bounds proach that computes discrete approximations of the 3D dis- on the spatial extent of Voronoi regions of each primitive as tance field and its application to medial axis computation well as spatial coherence between adjacent slices to cull the using the graphics hardware. Our contributions include: primitives. As a result, it can significantly reduce the load on the graphics pipeline. We have applied this technique 1. A novel site culling algorithm that uses Voronoi region to compute the Voronoi regions of large models composed properties to accelerate 3D distance field computation of tens of thousands of primitives. For a given grid size, 2. A technique for reducing the fill per slice using con- the culling efficiency increases with the model complexity. servative bounds on the Voronoi regions To demonstrate this technique, we compute the medial axis transform of a polyhedral model. -

Dena Slothower
Sketches & Applications 158 ComicDiary: Representing 176 Elastic Object Manipulation Using Chair Individual Experiences in Comics Coarse-to-fine Representation of Dena Slothower Style Mass-Spring Models 159 Compressing Large Polygonal 177 ELMO: A Head-Mounted Display Stanford University Models for Real-Time Image Synthesis 160 A Computationally Efficient 178 Elmo’s World: Digital Puppetry on Framework for Modeling Soft Body “Sesame Street” 140 Committee & Jury Impact 179 The Empathic Visualisation 141 Introduction 161 Computing 3D Geometry Directly Algorithm: Chernoff Faces from Range Images Revisited 142 “2001: An MR-Space Odyssey” 162 Computing Nearly Exact Visible 180 Enhanced Reality: A New Frontier Applying Mixed Reality Technology Sets within a Shaft with 4D for Computer Entertainment to VFX in Filmmaking Hierarchical Z-Buffering 181 Explicit Control of Topological 138 143 2D Shape Interpolation Using a 163 CONTIGRA: A High-Level XML- Evolution in 3D Mesh Morphing Hierarchical Approach Based Aprroach to Interactive 3D 182 Fair and Robust Curve Interpolation 144 3D Traffic Visualization in Real Components on the Sphere Time 164 Crashing Planes the Easy Way: 183 A Fast Simulating System for 145 ALVIN on the Web: Distributive Pearl Harbor Realistic Motion and Realistic Mission Rehearsal for a Deep 165 Creating Tools for PLAYSTA- Appearance of Fluids Submersible Vehicle TION2 Game Development 184 Fast-moving Water in DreamWorks’ 146 Analysis and Simulation of Facial 166 Creative Approaches to the “Spirit” Movements in Elicited and Posed -

Integration of Ray-Tracing Methods Into the Rasterisation Process University of Dublin, Trinity College
Integration of Ray-Tracing Methods into the Rasterisation Process by Shane Christopher, B.Sc. GMIT, B.Sc. DLIADT Dissertation Presented to the University of Dublin, Trinity College in fulfillment of the requirements for the Degree of MSc. Computer Science (Interactive Entertainment Technology) University of Dublin, Trinity College September 2010 Declaration I, the undersigned, declare that this work has not previously been submitted as an exercise for a degree at this, or any other University, and that unless otherwise stated, is my own work. Shane Christopher September 8, 2010 Permission to Lend and/or Copy I, the undersigned, agree that Trinity College Library may lend or copy this thesis upon request. Shane Christopher September 8, 2010 Acknowledgments I would like to thank my supervisor Michael Manzke as well as my course director John Dingliana for their help and guidance during this dissertation. I would also like to thank everyone who gave me support during the year and all my fellow members of the IET course for their friendship and the motivation they gave me. Shane Christopher University of Dublin, Trinity College September 2010 iv Integration of Ray-Tracing Methods into the Rasterisation Process Shane Christopher University of Dublin, Trinity College, 2010 Supervisor: Michael Manzke Visually realistic shadows in the field of computer games has been an area of constant research and development for many years. It is also considered one of the most costly in terms of performance when compared to other graphical processes. Most games today use shadow buffers which require rendering the scene multiple times for each light source. -

Powervr Graphics Keynote
PowerVR Graphics Keynote Rys Sommefeldt PowerVR Rogue Hardware PowerVR Rogue Recap Optional secondary message . Formally announced at CES 2012 . Tile-based deferred renderer . Building on technology proven over 5 previous generations . USC - Universal Shading Cluster . New scalar SIMD shader core . General purpose compute is a first class citizen in the core … . … while not forgetting what makes a shader core great for graphics facebook.com/imgtec @PowerVRInsider │ #idc15 3 TBDR Tile-based . Tile-based . Split each render up into small tiles (32x32 for the most part) . Bin geometry after vertex shading into those tiles . Tile-based rasterisation and pixel shading . Keep all data access for pixel shading on chip facebook.com/imgtec @PowerVRInsider │ #idc15 4 TBDR Deferred . Deferred rasterisation . Don’t actually get the GPU to do any pixel shading straight away . HW support for fully deferred rasterisation and then pixel shading . Rasterisation is pixel accurate facebook.com/imgtec @PowerVRInsider │ #idc15 5 End result . Bandwidth savings across all phases of rendering . Only fetch the geometry needed for the tile . Only process the visible pixels in the tile . Efficient processing . Maximise available computational resources . Do the best the hardware can with bandwidth facebook.com/imgtec @PowerVRInsider │ #idc15 6 Power . Maximising core efficiency . Lighting up the USC less often is always going to be a saving . Minimising bandwidth . Texturing less is a fantastic way to save power . Geometry fetch and binning is often more than 10% of per-frame bandwidth . Saves bandwidth for other parts of your render facebook.com/imgtec @PowerVRInsider │ #idc15 7 Rogue USC Architectural Building Block . Basic building block of the Rogue architecture . -

Realtime–Rendering with Opengl the Graphics Pipeline
Realtime{Rendering with OpenGL The Graphics Pipeline Francesco Andreussi Bauhaus{Universit¨atWeimar 14 November 2019 F. Andreussi (BUW) Realtime{Rendering with OpenGL 14 November 2019 1 / 16 Basic Information • Class every second week, 11:00{12:30 in this room, every change will be communicate to you as soon as possible via mail • Every time will be presented an assignment regarding the arguments covered by Prof. W¨uthrichand me to fulfil for the following class. It is possible (and also suggested) to work in couples • The submissions are to be done through push requests on Github and the work has to be presented in person scheduling an appointment with me Delays in the submissions and cheats (e.g. code copied from the Internet or other groups) WILL NOT be accepted! If you find code online DO NOT COPY IT but adapt and comment it, otherwise I have to consider it cheating and you will be rewarded with a 5.0 For any question you can write me at francesco.andreussi@uni{weimar.de F. Andreussi (BUW) Realtime{Rendering with OpenGL 14 November 2019 2 / 16 Graphics Processors & OpenGL A 3D scene is made of primitive shapes (i.e. points, lines and simple polygons), that are processed by the GPU asynchronously w.r.t. the CPU. OpenGL is a rendering library that exposes some functionality to the \Application level" and translates the commands for the GPU driver, which \speaks" forwards our directives to the graphic chip. Fig. 1: Communications between CPU and GPU F. Andreussi (BUW) Realtime{Rendering with OpenGL 14 November 2019 3 / 16 OpenGL OpenGL is an open standard and cross-platform API. -

Performance Comparison on Rendering Methods for Voxel Data
fl Performance comparison on rendering methods for voxel data Oskari Nousiainen School of Science Thesis submitted for examination for the degree of Master of Science in Technology. Espoo July 24, 2019 Supervisor Prof. Tapio Takala Advisor Dip.Ins. Jukka Larja Aalto University, P.O. BOX 11000, 00076 AALTO www.aalto.fi Abstract of the master’s thesis Author Oskari Nousiainen Title Performance comparison on rendering methods for voxel data Degree programme Master’s Programme in Computer, Communication and Information Sciences Major Computer Science Code of major SCI3042 Supervisor Prof. Tapio Takala Advisor Dip.Ins. Jukka Larja Date July 24, 2019 Number of pages 50 Language English Abstract There are multiple ways in which 3 dimensional objects can be presented and rendered to screen. Voxels are a representation of scene or object as cubes of equal dimensions, which are either full or empty and contain information about their enclosing space. They can be rendered to image by generating surface geometry and passing that to rendering pipeline or using ray casting to render the voxels directly. In this paper, these methods are compared to each other by using different octree structures for voxel storage. These methods are compared in different generated scenes to determine which factors affect their relative performance as measured in real time it takes to draw a single frame. These tests show that ray casting performs better when resolution of voxel model is high, but rasterisation is faster for low resolution voxel models. Rasterisation scales better with screen resolution and on higher screen resolutions most of the tested voxel resolutions where faster to render with with rasterisation. -

Les Cartes Graphiques/Version Imprimable — Wik
Les cartes graphiques/Version imprimable — Wik... https://fr.wikibooks.org/w/index.php?title=Les_c... Un livre de Wikilivres. Les cartes graphiques Une version à jour et éditable de ce livre est disponible sur Wikilivres, une bibliothèque de livres pédagogiques, à l'URL : http://fr.wikibooks.org/wiki/Les_cartes_graphiques Vous avez la permission de copier, distribuer et/ou modifier ce document selon les termes de la Licence de documentation libre GNU, version 1.2 ou plus récente publiée par la Free Software Foundation ; sans sections inaltérables, sans texte de première page de couverture et sans Texte de dernière page de couverture. Une copie de cette licence est incluse dans l'annexe nommée « Licence de documentation libre GNU ». 1 sur 35 24/02/2017 01:10 Les cartes graphiques/Version imprimable — Wik... https://fr.wikibooks.org/w/index.php?title=Les_c... Les cartes d'affichage Les cartes graphiques sont des cartes qui s'occupent de communiquer avec l'écran, pour y afficher des images. Au tout début de l'informatique, ces opérations étaient prises en charge par le processeur : celui-ci calculait l'image à afficher à l'écran, et l'envoyait pixel par pixel à l'écran, ceux-ci étant affichés immédiatement après. Cela demandait de synchroniser l'envoi des pixels avec le rafraichissement de l'écran. Pour simplifier la vie des programmeurs, les fabricants de matériel ont inventé des cartes d'affichage, ou cartes vidéo. Avec celles-ci, le processeur calcule l'image à envoyer à l'écran, et la transmet à la carte d'affichage. Celle-ci prend alors en charge son affichage à l'écran, déchargeant le processeur de cette tâche.