Non-Radial Pulsations in the O Stars Ξ Persei and Λ Cephei
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Today Our Place in the Universe
Our place in the Universe , and other sources ully T , Bob Patterson, Donna Cox (NCSA), Data: Hipparcos, Brent iz: Stuart Levy V Tom Abel Today KIPAC The Birth, Life & Aftermath of the First Stars Tom Abel KIPAC/Stanford work with Matt Turk (Birth) John Wise (Life) Ralf Kähler (Scientific Visualization) Outline • Conception • A difficult birth • A surprising life • Remarkable consequences • Three-D radiation transport around point sources • Spatially & temporally structured adaptive cosmological & relativistic hydrodynamics • public version of enzo at: http://lca.ucsd.edu/portal/software/enzo Discovery by How we find things: Computer? 6 6.28 Conception Physics problem: • Initial Conditions: COBE/ACBAR/ Boomerang/WMAP/CfA/SDDS/ 2DF/CDMS/DAMA/Edelweiss/... + Theory: Constituents, Density Fluctuations, Thermal History • Physics: Gravity, MHD, Chemistry, Radiative Cooling, Radiation Transport, Cosmic Rays, Dust drift & cooling, Supernovae, Stellar evolution, etc. Ralf Kähler & Tom Abel for PBS • Transition from Linear to Non- Origins. Aired Dec 04 Linear: • Using patched based structured adaptive (space & time) mesh refinement Making a proto-star Simulation: Tom Abel (KIPAC/Stanford), Greg Bryan (Columbia), Mike Norman (UCSD) Viz: Ralf Kähler (AEI, ZIB, KIPAC), Bob Patterson, Stuart Levy, Donna Cox (NCSA), Tom Abel © “The Unfolding Universe” Discovery Channel 2002 Dynamic range ~1e12. Typically 3 solar mass dm particles > 30 levels of refinement > 8 cells per local Jeans Length tens of thousands of grid patches non-equilibrium chemistry dynamically load balanced RT effects above 1e12 cm-3 Zoom in MPI. 16 processors enough Turk & Abel in prep Note disks within disks happen routinely in turbulent collapses! Mass Scales? Kelvin Helmholtz time at ZAMS Abel, Bryan & Norman 2002 Recap First Stars are isolated and very massive • Theoretical uncertainty: 30 - 300 solar mass Many simulations with three different numerical techniques and a large range of numerical resolutions have converged to this result. -

October, 2011
IN THIS ISSUE: OCTOBER 2011 Event Calendar, News Notes Minutes of the September Meeting MVAS Reminders: Party-on MVAS Activities: On The Road Again Observer’s Notes: Variable Heroines MVAS Homework: M-76, Little Dumbbell Homework Charts: Algol, asteroid (15) Eunomia Constellation of the Month: Perseus November 2011 Sky Almanac Gallery: Comet Quest, Summer Photos Meteorite Editor: Phil Plante 1982 Mathews Rd. #2 Youngstown OH 44514 OCTOBER 2011 NEWS NOTES Newsletter of the Mahoning Valley Astronomical Society, Inc. The Big Ear. Lofar (Low Frequency Array) is a new kind of radio telescope. It can see radio waves with low frequencies, similar to those that give us FM radio. Rather than collecting MVAS CALENDAR signals from individual radio sources, Lofar continuously monitors large swathes of sky. Lofar is more sensitive to the OCT 22 Business meeting at the MVCO 8:00 PM longest observable radio waves than any other telescope. It can OCT 29 Halloween Party at the MVCO 7:00 PM see many billions of light years out into space, back to the time before the first stars formed, a few hundred million years after NOV17/18 Leonid Meteor watch. On your own? Midnight… the Big Bang. On Monday, September 21, 2011, Sweden's Minister for Education and Research, Jan Bjorklund, opened the NOV 19 Business meeting at YSU. Show at 8:00 PM Onsala Space Observatory's newest telescope; to become part NOV 26 Star Party at the MVCO. 7:00 PM till…. of Lofar, which is the world's largest radio telescope. The 192 new radio antennas at Onsala's Lofar station will be linked together with 47 similar stations over the whole of NATIONAL & REGIONAL EVENTS Europe, and sent over the Internet to a central supercomputer in OCT 24 - 30 CSPG Fall Star Party, held in Chiefland, FL . -

Patrick Moore's Practical Astronomy Series
Patrick Moore’s Practical Astronomy Series Other Titles in this Series Telescopes and Techniques (2nd Edn.) Observing the Planets Chris Kitchin Peter T. Wlasuk The Art and Science of CCD Astronomy Light Pollution David Ratledge (Ed.) Bob Mizon The Observer’s Year Using the Meade ETX Patrick Moore Mike Weasner Seeing Stars Practical Amateur Spectroscopy Chris Kitchin and Robert W. Forrest Stephen F. Tonkin (Ed.) Photo-guide to the Constellations More Small Astronomical Observatories Chris Kitchin Patrick Moore (Ed.) The Sun in Eclipse Observer’s Guide to Stellar Evolution Michael Maunder and Patrick Moore Mike Inglis Software and Data for Practical Astronomers How to Observe the Sun Safely David Ratledge Lee Macdonald Amateur Telescope Making The Practical Astronomer’s Deep-Sky Stephen F. Tonkin (Ed.) Companion Observing Meteors, Comets, Supernovae and Jess K. Gilmour other Transient Phenomena Observing Comets Neil Bone Nick James and Gerald North Astronomical Equipment for Amateurs Observing Variable Stars Martin Mobberley Gerry A. Good Transit: When Planets Cross the Sun Visual Astronomy in the Suburbs Michael Maunder and Patrick Moore Antony Cooke Practical Astrophotography Astronomy of the Milky Way: The Observer’s Jeffrey R. Charles Guide to the Northern and Southern Milky Way Observing the Moon (2 volumes) Peter T. Wlasuk Mike Inglis Deep-Sky Observing The NexStar User Guide Steven R. Coe Michael W. Swanson AstroFAQs Observing Binary and Double Stars Stephen F. Tonkin Bob Argyle (Ed.) The Deep-Sky Observer’s Year Navigating the Night Sky Grant Privett and Paul Parsons Guilherme de Almeida Field Guide to the Deep Sky Objects The New Amateur Astronomer Mike Inglis Martin Mobberley Choosing and Using a Schmidt-Cassegrain Care of Astronomical Telescopes and Telescope Accessories Rod Mollise M. -

GTO Keypad Manual, V5.001
ASTRO-PHYSICS GTO KEYPAD Version v5.xxx Please read the manual even if you are familiar with previous keypad versions Flash RAM Updates Keypad Java updates can be accomplished through the Internet. Check our web site www.astro-physics.com/software-updates/ November 11, 2020 ASTRO-PHYSICS KEYPAD MANUAL FOR MACH2GTO Version 5.xxx November 11, 2020 ABOUT THIS MANUAL 4 REQUIREMENTS 5 What Mount Control Box Do I Need? 5 Can I Upgrade My Present Keypad? 5 GTO KEYPAD 6 Layout and Buttons of the Keypad 6 Vacuum Fluorescent Display 6 N-S-E-W Directional Buttons 6 STOP Button 6 <PREV and NEXT> Buttons 7 Number Buttons 7 GOTO Button 7 ± Button 7 MENU / ESC Button 7 RECAL and NEXT> Buttons Pressed Simultaneously 7 ENT Button 7 Retractable Hanger 7 Keypad Protector 8 Keypad Care and Warranty 8 Warranty 8 Keypad Battery for 512K Memory Boards 8 Cleaning Red Keypad Display 8 Temperature Ratings 8 Environmental Recommendation 8 GETTING STARTED – DO THIS AT HOME, IF POSSIBLE 9 Set Up your Mount and Cable Connections 9 Gather Basic Information 9 Enter Your Location, Time and Date 9 Set Up Your Mount in the Field 10 Polar Alignment 10 Mach2GTO Daytime Alignment Routine 10 KEYPAD START UP SEQUENCE FOR NEW SETUPS OR SETUP IN NEW LOCATION 11 Assemble Your Mount 11 Startup Sequence 11 Location 11 Select Existing Location 11 Set Up New Location 11 Date and Time 12 Additional Information 12 KEYPAD START UP SEQUENCE FOR MOUNTS USED AT THE SAME LOCATION WITHOUT A COMPUTER 13 KEYPAD START UP SEQUENCE FOR COMPUTER CONTROLLED MOUNTS 14 1 OBJECTS MENU – HAVE SOME FUN! -

December 2019 BRAS Newsletter
A Monthly Meeting December 11th at 7PM at HRPO (Monthly meetings are on 2nd Mondays, Highland Road Park Observatory). Annual Christmas Potluck, and election of officers. What's In This Issue? President’s Message Secretary's Summary Outreach Report Asteroid and Comet News Light Pollution Committee Report Globe at Night Member’s Corner – The Green Odyssey Messages from the HRPO Friday Night Lecture Series Science Academy Solar Viewing Stem Expansion Transit of Murcury Edge of Night Natural Sky Conference Observing Notes: Perseus – Rescuer Of Andromeda, or the Hero & Mythology Like this newsletter? See PAST ISSUES online back to 2009 Visit us on Facebook – Baton Rouge Astronomical Society Baton Rouge Astronomical Society Newsletter, Night Visions Page 2 of 25 December 2019 President’s Message I would like to thank everyone for having me as your president for the last two years . I hope you have enjoyed the past two year as much as I did. We had our first Members Only Observing Night (MOON) at HRPO on Sunday, 29 November,. New officers nominated for next year: Scott Cadwallader for President, Coy Wagoner for Vice- President, Thomas Halligan for Secretary, and Trey Anding for Treasurer. Of course, the nominations are still open. If you wish to be an officer or know of a fellow member who would make a good officer contact John Nagle, Merrill Hess, or Craig Brenden. We will hold our annual Baton Rouge “Gastronomical” Society Christmas holiday feast potluck and officer elections on Monday, December 9th at 7PM at HRPO. I look forward to seeing you all there. ALCon 2022 Bid Preparation and Planning Committee: We’ll meet again on December 14 at 3:00.pm at Coffee Call, 3132 College Dr F, Baton Rouge, LA 70808, UPCOMING BRAS MEETINGS: Light Pollution Committee - HRPO, Wednesday December 4th, 6:15 P.M. -

108 Afocal Procedure, 105 Age of Globular Clusters, 25, 28–29 O
Index Index Achromats, 70, 73, 79 Apochromats (APO), 70, Averted vision Adhafera, 44 73, 79 technique, 96, 98, Adobe Photoshop Aquarius, 43, 99 112 (software), 108 Aquila, 10, 36, 45, 65 Afocal procedure, 105 Arches cluster, 23 B1620-26, 37 Age Archinal, Brent, 63, 64, Barkhatova (Bar) of globular clusters, 89, 195 catalogue, 196 25, 28–29 Arcturus, 43 Barlow lens, 78–79, 110 of open clusters, Aricebo radio telescope, Barnard’s Galaxy, 49 15–16 33 Basel (Bas) catalogue, 196 of star complexes, 41 Aries, 45 Bayer classification of stellar associations, Arp 2, 51 system, 93 39, 41–42 Arp catalogue, 197 Be16, 63 of the universe, 28 Arp-Madore (AM)-1, 33 Beehive Cluster, 13, 60, Aldebaran, 43 Arp-Madore (AM)-2, 148 Alessi, 22, 61 48, 65 Bergeron 1, 22 Alessi catalogue, 196 Arp-Madore (AM) Bergeron, J., 22 Algenubi, 44 catalogue, 197 Berkeley 11, 124f, 125 Algieba, 44 Asterisms, 43–45, Berkeley 17, 15 Algol (Demon Star), 65, 94 Berkeley 19, 130 21 Astronomy (magazine), Berkeley 29, 18 Alnilam, 5–6 89 Berkeley 42, 171–173 Alnitak, 5–6 Astronomy Now Berkeley (Be) catalogue, Alpha Centauri, 25 (magazine), 89 196 Alpha Orionis, 93 Astrophotography, 94, Beta Pictoris, 42 Alpha Persei, 40 101, 102–103 Beta Piscium, 44 Altair, 44 Astroplanner (software), Betelgeuse, 93 Alterf, 44 90 Big Bang, 5, 29 Altitude-Azimuth Astro-Snap (software), Big Dipper, 19, 43 (Alt-Az) mount, 107 Binary millisecond 75–76 AstroStack (software), pulsars, 30 Andromeda Galaxy, 36, 108 Binary stars, 8, 52 39, 41, 48, 52, 61 AstroVideo (software), in globular clusters, ANR 1947 -

Milestone Goto-Bino Series .Cdr
Kson MilestoneK Standard Alt/Az GOTO Mount INSTRUCTIONS CONTENT FOR KSON STANDARD ALT/AZ GOTO USER INTRODUCTION.................................................................................1 ACCESSORIES..................................................................................2 ASSEMBLY INSTRUCTIONS.............................................................3 FEATURES.........................................................................5 OPERATION MANUAL FOR SKYTOUCH CONTROLLER............... 6 KEY DESCRIPTION.................................................................................6 STATUS DESCRIPTION...........................................................................6 OPERATION PROCESS...........................................................................7 POWER ON......................................................................................7 WARNING........................................................................................7 ALIGNMENT STATUS........................................................................7 CHANGE THE DATE..................................................................7 CHANGE THE TIME...................................................................8 CHANGE THE SITE...................................................................8 ALIGNMENT.............................................................................9 NAVIGATION STATUS.....................................................................11 MENU STATUS................................................................................11 -

GTO KEYPAD Version V4.19.3
ASTRO-PHYSICS GTO KEYPAD Version v4.19.3 Flash RAM Updates Keypad flash RAM updates can be accomplished through the Internet. Check our web site www.astro-physics.com periodically for further information. July 29, 2016 Contents About this mAnuAl 5 GTO KeypAd ContRolleR 6 layout and buttons of the Keypad 6 Vacuum Fluorescent display 6 n-s-e-W directional buttons 6 RA/deC ReV button: 6 STOP button 7 number buttons 7 <pReV and neXt> buttons 7 Goto button 7 ± button 7 menu button 7 FoC button 7 Retractable hanger 7 Keypad protector 7 installation: 8 Keypad Care and Warranty 8 Warranty 8 Keypad battery for 256K memory boards 8 Keypad battery for 512K memory boards 8 Cleaning Keypad display 8 temperature Ratings 8 GettinG stARted – do this At home, iF possible 9 setup your mount and Cable Connections 9 Gather basic information 9 enter your location, date and time 9 practice using your Keypad 11 youR FiRst obseRVinG session & FoR poRtAble mounts 12 normal startup sequence for mounts that are in the field 12 Assemble your mount 12 startup sequence 12 star sync 12 Resume last position 13 new setup → new setup start From park position (press 1, 2, 3, or 4) 13 helpful hints 13 AUTO-ConneCt seQuenCe – FoR peRmAnent, polAR-AliGned mounts 14 important points 14 eXteRnAl stARtup seQuenCe – FoR ComputeR ContRolled mounts 15 important points 15 polAR AliGnment – WhiCh method to Choose? 16 n polar Calibrate - Calibrating with polaris 16 two-star Calibration 17 polar Aligning in the daytime – northern hemisphere 20 polar Aligning in the daytime – southern -

The Universe Contents 3 HD 149026 B
History . 64 Antarctica . 136 Utopia Planitia . 209 Umbriel . 286 Comets . 338 In Popular Culture . 66 Great Barrier Reef . 138 Vastitas Borealis . 210 Oberon . 287 Borrelly . 340 The Amazon Rainforest . 140 Titania . 288 C/1861 G1 Thatcher . 341 Universe Mercury . 68 Ngorongoro Conservation Jupiter . 212 Shepherd Moons . 289 Churyamov- Orientation . 72 Area . 142 Orientation . 216 Gerasimenko . 342 Contents Magnetosphere . 73 Great Wall of China . 144 Atmosphere . .217 Neptune . 290 Hale-Bopp . 343 History . 74 History . 218 Orientation . 294 y Halle . 344 BepiColombo Mission . 76 The Moon . 146 Great Red Spot . 222 Magnetosphere . 295 Hartley 2 . 345 In Popular Culture . 77 Orientation . 150 Ring System . 224 History . 296 ONIS . 346 Caloris Planitia . 79 History . 152 Surface . 225 In Popular Culture . 299 ’Oumuamua . 347 In Popular Culture . 156 Shoemaker-Levy 9 . 348 Foreword . 6 Pantheon Fossae . 80 Clouds . 226 Surface/Atmosphere 301 Raditladi Basin . 81 Apollo 11 . 158 Oceans . 227 s Ring . 302 Swift-Tuttle . 349 Orbital Gateway . 160 Tempel 1 . 350 Introduction to the Rachmaninoff Crater . 82 Magnetosphere . 228 Proteus . 303 Universe . 8 Caloris Montes . 83 Lunar Eclipses . .161 Juno Mission . 230 Triton . 304 Tempel-Tuttle . 351 Scale of the Universe . 10 Sea of Tranquility . 163 Io . 232 Nereid . 306 Wild 2 . 352 Modern Observing Venus . 84 South Pole-Aitken Europa . 234 Other Moons . 308 Crater . 164 Methods . .12 Orientation . 88 Ganymede . 236 Oort Cloud . 353 Copernicus Crater . 165 Today’s Telescopes . 14. Atmosphere . 90 Callisto . 238 Non-Planetary Solar System Montes Apenninus . 166 How to Use This Book 16 History . 91 Objects . 310 Exoplanets . 354 Oceanus Procellarum .167 Naming Conventions . 18 In Popular Culture . -
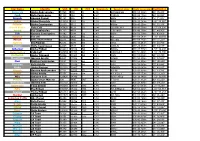
Star Name Identity SAO HD FK5 Magnitude Spectral Class Right Ascension Declination Alpheratz Alpha Andromedae 73765 358 1 2,06 B
Star Name Identity SAO HD FK5 Magnitude Spectral class Right ascension Declination Alpheratz Alpha Andromedae 73765 358 1 2,06 B8IVpMnHg 00h 08,388m 29° 05,433' Caph Beta Cassiopeiae 21133 432 2 2,27 F2III-IV 00h 09,178m 59° 08,983' Algenib Gamma Pegasi 91781 886 7 2,83 B2IV 00h 13,237m 15° 11,017' Ankaa Alpha Phoenicis 215093 2261 12 2,39 K0III 00h 26,283m - 42° 18,367' Schedar Alpha Cassiopeiae 21609 3712 21 2,23 K0IIIa 00h 40,508m 56° 32,233' Deneb Kaitos Beta Ceti 147420 4128 22 2,04 G9.5IIICH-1 00h 43,590m - 17° 59,200' Achird Eta Cassiopeiae 21732 4614 3,44 F9V+dM0 00h 49,100m 57° 48,950' Tsih Gamma Cassiopeiae 11482 5394 32 2,47 B0IVe 00h 56,708m 60° 43,000' Haratan Eta ceti 147632 6805 40 3,45 K1 01h 08,583m - 10° 10,933' Mirach Beta Andromedae 54471 6860 42 2,06 M0+IIIa 01h 09,732m 35° 37,233' Alpherg Eta Piscium 92484 9270 50 3,62 G8III 01h 13,483m 15° 20,750' Rukbah Delta Cassiopeiae 22268 8538 48 2,66 A5III-IV 01h 25,817m 60° 14,117' Achernar Alpha Eridani 232481 10144 54 0,46 B3Vpe 01h 37,715m - 57° 14,200' Baten Kaitos Zeta Ceti 148059 11353 62 3,74 K0IIIBa0.1 01h 51,460m - 10° 20,100' Mothallah Alpha Trianguli 74996 11443 64 3,41 F6IV 01h 53,082m 29° 34,733' Mesarthim Gamma Arietis 92681 11502 3,88 A1pSi 01h 53,530m 19° 17,617' Navi Epsilon Cassiopeiae 12031 11415 63 3,38 B3III 01h 54,395m 63° 40,200' Sheratan Beta Arietis 75012 11636 66 2,64 A5V 01h 54,640m 20° 48,483' Risha Alpha Piscium 110291 12447 3,79 A0pSiSr 02h 02,047m 02° 45,817' Almach Gamma Andromedae 37734 12533 73 2,26 K3-IIb 02h 03,900m 42° 19,783' Hamal Alpha -

CONSTELLATION PERSEUS the Constellation Perseus Is a Constellation in the Northern Sky Which Was Named After the Greek Mythological Hero Perseus
CONSTELLATION PERSEUS The constellation Perseus is a constellation in the northern sky which was named after the Greek mythological hero Perseus. It is located in the northern celestial hemisphere near several other constellations named after ancient Greek legends surrounding Perseus, including Andromeda to the west and Cassiopeia to the north. One of the 48 constellations listed by the 2nd-century astronomer Ptolemy, it is still among the 88 modern constellations as defined by the International Astronomical Union GENERAL Perseus is also bordered by Aries and Taurus to the south, Auriga to the east, Camelopardalis to the north, and Triangulum to the west. Some star atlases during the early 19th century also depicted Perseus holding onto the head of the Medusa, whose asterism was named together as Perseus et Caput Medusae, however, this never came into popular usage. The galactic plane of the Milky Way passes through Perseus but is mostly obscured by molecular clouds. The constellation's brightest star is the yellow-white supergiant Alpha Persei (also called Mirfak or Mirphak), which shines at magnitude 1.79. It and many of the surrounding stars are members of an open cluster known as the Alpha Persei Cluster. The best-known star, however, is Algol (Beta Persei), linked with ominous legends because of its variability, which is noticeable to the naked eye. Rather than being an intrinsically variable star, it is an eclipsing Perseus carrying the head of Medusa the Gorgon, as depicted in binary. Other notable star systems in Perseus Urania's Mirror, a set of cards published in London c.1825 include X Persei, a binary system containing a neutron star, and GK Persei, a nova that peaked at magnitude 0.2 in 1901. -

Deep Sky Delights in Andromeda, Perseus and Triangulum
Image created with SkySafari 5 for Mac OS X, ©2010-2016 Simulation Curriculum Corp., skysafariastronomy.com. The Monthly Sky Guide October 2020 Late October is normally the part of the year that finds those of us in the UK and Europe reverting to standard time (CET/GMT). This is normally greeted with groans by those outside the astronomical community, as it leads to it getting darker earlier - those of us of a more astronomcial inclination will feel somewhat different, as it increases the opportunity for observations at a reasonable hour of the evening. In the UK, the clocks go back on Sunday 25th October this year. Those in North America will have to wait until the early part of November for this changeover to take place. Naturally, what happens in the Northern Hemisphere has the opposite effect in the Southern. Those in many territories in Australia and Brazil will begin their Daylight Saving Time (Summer Time) in October (New Zealand and Chile having started their DSTs somewhat earlier). Wherever you find yourself in the world, there's plenty going on in the skies above us this month... The Solar System The Moon The Moon starts October in Cetus, at Full phase. The Moon will rise at a little after 7pm (BST) and be transiting in the south a little after midnight, the following morning. Naturally, around the beginning of the month isn’t the greatest part of the month for visual deep sky observations, or imaging without narrowband filtration. The Moon will reach Last Quarter on the 10th, when it will be found in the constellation of Gemini.