DOCSLIB.ORG

Modeling Radial Velocity Signals for Exoplanet Search Applications

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modeling Radial Velocity Signals for Exoplanet Search Applications MODELING RADIAL VELOCITY SIGNALS FOR EXOPLANET SEARCH APPLICATIONS Prabhu Babu∗, Petre Stoica Division of Systems and Control, Department of Information Technology Uppsala University, P.O. Box 337, SE-75 105, Uppsala, Sweden Jian Li Department of Electrical and Computer Engineering, University of Florida, Gainesville, 32611, FL, U.S.A. Keywords: Radial velocity method, Exoplanet search, Kepler model, IAA, Periodogram, RELAX, GLRT. Abstract: In this paper, we introduce an estimation technique for analyzing radial velocity data commonly encountered in extrasolar planet detection. We discuss the Keplerian model for radial velocity data measurements and estimate the 3D spectrum (power vs. eccentricity, orbital period and periastron passage time) of the radial velocity data by using a relaxation maximum likelihood algorithm (RELAX). We then establish the significance of the spectral peaks by using a generalized likelihood ratio test (GLRT). Numerical experiments are carried out on a real life data set to evaluate the performance of our method. 1 INTRODUCTION on iterative deconvolution in the frequency domain to obtain a clean spectrum from an initial dirty one. A Extrasolar planet (or shortly exoplanet) detection is periodogram related method is the least squares peri- a fascinating and challenging area of research in the odogram (also called the Lomb-Scargle periodogram) field of astrophysics. Till mid 2009, 353 exoplanets (Lomb, 1976; Scargle, 1982) which estimates the si- have been discovered. Some of the techniques avail- nusoidal components by fitting them to the observed able in the astrophysics literature to detect exoplanets data. Most recently, (Yardibi et al., 2010; Stoica et al., are astrometry, the radial velocity method, pulsar tim- 2009) introduced a new method called the Iterative ing, the transit method and gravitational microlens- Adaptive Approach (IAA), which relies on solving an ing. Among these methods, the radial velocity analy- iterative weighted least squares problem. sis is the most commonlyused technique, in which the In this paper, we analyze the radial velocity data Doppler shift in the spectral lines and hence the radial by using a relaxation maximum likelihood algorithm velocity of the parent star is measured. The spectrum (RELAX) initialized with IAA estimates. The signif- of the measured Doppler shifts is then analyzed to de- icance of the spectral peaks is then established via a tect the exoplanet(s) revolving around the star. generalized likelihood ratio test (GLRT). Numerical Most often the radial velocity measurements are ob- experiments are carried out on a real life radial veloc- tained at nonuniformly spaced time intervals due to ity data set. hardware and practical constraints, which limits the In Section 2, we describe the model used in this pa- application of commonly used spectral analysis meth- per for the radial velocity data. Section 3 presents the ods. The most straightforward way to deal with this RELAX and GLRT methods, and Section 4 contains problem is to use the standard periodogram by ignor- the results for a real life example. Finally, the paper ing the nonuniformity of data samples, which results is concluded in Section 5. in an inaccurate spectrum. In (Roberts et al., 1987), a method named CLEAN was proposed, which is based ∗Corresponding author. This work was supported in part by the Swedish Research Council (VR). 155 Babu P., Stoica P. and Li J. (2010). MODELING RADIAL VELOCITY SIGNALS FOR EXOPLANET SEARCH APPLICATIONS. In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 155-159 DOI: 10.5220/0002770601550159 Copyright c SciTePress ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics 2 DATA MODEL enough (to reduce the computation time), then IAA might miss some true peaks (see (Babu et al., 2010) N Let {y(tn)}n=1 denote the radial velocity of a star for an elaborate discussion on IAA for radial veloc- measured at a set of possibly nonuniform time in- ity data). In that case, applying RELAX (Li and N stants {tn}n=1. Based on the Keplerian model of plan- Stoica, 1996), a parametric iterative estimation al- etary motion (Zechmeister and Kurster, 2009) (Cum- gorithm, can refine the IAA estimates. Algorithm 1 ming, 2004), the radial velocity data are modeled as briefly describes the steps involved in RELAX. The follows: P largest peaks picked from IAA are used as initial M estimates for RELAX, which has a beneficial effect β ω ν ω y(tn)= C0 + ∑ m[cos( m + m(tn)) + em cos( m)], on the convergence of RELAX compared with using m=1 n = 1,··· ,N other more arbitrary initial estimates. In the case of (1) radial velocity data, the choice of P = 5 peaks ap- pears to be reasonable for most applications. RELAX where C0 is the constant radial velocity, and generally converges within a few iterations (typically 1+em tan(νm(tn)) = tan(Em(tn)) in less than 10 iterations). 1−em (2) q 2π(tn−Tm) Next we note that, under the assumption the noise Em(tn) − em sin(Em(tn)) = , Pm in the data is Gaussian distributed, the RELAX esti- M: Number of exoplanets revolving around the mates are optimal in the maximum likelihood sense star. The number of planets M is usually unknown. (Li and Stoica, 1996). We can then use the general- th em: Eccentricity of the orbit of the m planet. ized likelihood ratio test (GLRT) to establish the sta- th ωm: Longitudeof the periastron for the m planet. tistical significance of the estimated planet parame- th Pm: Orbital period of the m planet; Pm is related ters. We first apply RELAX to the largest IAA peak to orbital frequency f by f = 1 . m m Pm and use GLRT to test the null hypothesisthat there are th Tm: Periastron passage time of the m planet. no planets (or, in other words, that the data is made th βm: Radial velocity amplitude of the m planet. only of white noise) against the hypothesis that there νm(tn), Em(tn): True and eccentric anomaly of the is at least one exoplanet. If the test rejects the null th m planet, with tn denoting their time dependence. hypothesis then we will proceed and apply RELAX We divide the entire 2D space G, defined as G = to the two largest peaks and subsequently test the hy- fmax fmax pothesis that there is one exoplanet in the data against {(e, f ), 0 ≤ e < emax, − 2 < f < 2 }, into a grid of prespecified size K. We point out here that the grid the hypothesis that there are at least two exoplanets; G does not include the parameter T , and that T is and so on. As an example, for the following hypothe- taken to be zero for the time being but will be esti- ses H : There are no planets. mated as described later on. The choices of emax and 0 f in G depend on the sampling pattern: to deter- H1: There is at least one exoplanet with eccentricity max ˆ mine them, we calculate the spectral window defined eˆ1, orbital frequency f1 and periastron passage time ˆ as: T1. the log-likelihood (LL) functions are given by: N 2 1 W (e, f ) = ∑ exp( jν(tn)) , 0 ≤ e < 1,−∞ ≤ f ≤ ∞. N LL(H ) = n=1 0 (3) N N ∑ 2 ν − 2 ln |y(tn)| +C, For any choice of (e, f ) and tn, there exists a (tn) ob- n=1 tained via (2). Following (Eyer and Bartholdi, 1999), LL(H1) = N the parameters emax and fmax are chosen such that the N ∑ ν ν 2 − 2 ln |y(tn) − rˆ1 cos( (tn)) − qˆ1 sin( (tn))| +C region G leads to an unambiguous W(e, f ) (see (Babu n=1 et al., 2010) for more details). (4) where C is an additive constant, ν(tn) is calculated from the RELAX estimates (ˆe1, fˆ1, Tˆ1), andr ˆ1,qˆ1 3 PARAMETER ESTIMATION are the least square estimates of r,q corresponding to (ˆe1, fˆ1, Tˆ1), see Algorithm 1. Under the assumption AND STATISTICAL that hypothesis H0 is true, the log-likelihood-ratio, SIGNIFICANCE TESTING: defined as 2(LL(H1) − LL(H0)), is asymptotically a RELAX AND GLRT random variable with a chi-square distribution. Then the GLRT is given by The estimates obtained from IAA are usually fairly H1 2(LL(H ) − LL(H )) ≷ Λ (5) accurate. However, if the grid ( ) is not chosen fine 1 0 G H0 156 MODELING RADIAL VELOCITY SIGNALS FOR EXOPLANET SEARCH APPLICATIONS where Λ denotes a fixed threshold. The threshold is of spectral peaks (planets) in radial velocity data and usually chosen such that prob(X ≤ Λ)= ξ, where X ∼ accurately identifies both their frequencies and eccen- χ2 5 denotes a chi-square distributed random variable tricities as well as their periastron passage times. The with 5 degreesof freedom(becauseof the 5 unknowns example used here is typical of cases usually encoun- per planet in the data model, namely e, f , T , r and tered in exoplanet search and hence the proposed al- q), and ξ determines the significance level of the test. gorithm is believed to be an effective and useful tool. Choosing ξ = 0.99 gives a false alarm probability of 0.01 and the corresponding threshold is Λ = 15. REFERENCES 4 A REAL LIFE EXAMPLE: Babu, P., Stoica, P., Li, J., Chen, Z., and Ge, J. (2010). Analysis of radial velocity data by a novel adaptive HD 208487 approach. The Astronomical Journal, 139:783–793. Cumming, A. (2004). Detectability of extrasolar planets in In this section, we consider the application of the al- radial velocity surveys. Monthly Notices of the Royal gorithm introduced in the previous section to a real Astronomical Society, 354(4):1165–1176.
Load more

Recommended publications
  • Disertaciones Astronómicas Boletín Número 69 De Efemérides Astronómicas 17 De Marzo De 2021
    Disertaciones astronómicas Boletín Número 69 de efemérides astronómicas 17 de marzo de 2021 Realiza Luis Fernando Ocampo O. ([email protected]). Noticias de la semana. La Luz Zodiacal y su origen. Imagen 1: Imagen de la Luz Zodiacal hacia el este, junto antes del amanecer. Crédito: spacew.com/gallery/DominicCantin&gt. La luz zodiacal (también llamada falso amanecer cuando se ve antes del amanecer) es un resplandor blanco tenue, difuso y aproximadamente triangular que es visible en el cielo nocturno y parece extenderse desde la dirección del Sol y a lo largo del zodíaco, en el sentido de la eclíptica. La luz solar dispersada por el polvo interplanetario provoca este fenómeno. Sin embargo, el brillo es tan tenue que la luz de la luna y / o la contaminación lumínica lo eclipsan, haciéndolo invisible. El polvo interplanetario en el Sistema Solar forma colectivamente una nube gruesa con forma de panqueque llamada nube zodiacal, que se extiende a ambos lados del plano de la eclíptica. Los tamaños de partículas oscilan entre 10 y 300 micrómetros, lo que implica masas desde un nanogramo hasta decenas de microgramos. Las observaciones de la nave espacial Pioneer 10 en la década de 1970 vincularon la luz zodiacal con la nube de polvo interplanetaria en el Sistema Solar. En las latitudes medias, la luz zodiacal se observa mejor en el cielo occidental en la primavera después de que el crepúsculo vespertino ha desaparecido por completo, o en el cielo oriental en otoño, justo antes de que aparezca el crepúsculo matutino. La luz zodiacal aparece como una columna, más brillante en el horizonte, inclinada en el ángulo de la eclíptica.
    [Show full text]
  • Li Abundances in F Stars: Planets, Rotation, and Galactic Evolution,
    A&A 576, A69 (2015) Astronomy DOI: 10.1051/0004-6361/201425433 & c ESO 2015 Astrophysics Li abundances in F stars: planets, rotation, and Galactic evolution, E. Delgado Mena1,2, S. Bertrán de Lis3,4, V. Zh. Adibekyan1,2,S.G.Sousa1,2,P.Figueira1,2, A. Mortier6, J. I. González Hernández3,4,M.Tsantaki1,2,3, G. Israelian3,4, and N. C. Santos1,2,5 1 Centro de Astrofisica, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal e-mail: [email protected] 2 Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal 3 Instituto de Astrofísica de Canarias, C/via Lactea, s/n, 38200 La Laguna, Tenerife, Spain 4 Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain 5 Departamento de Física e Astronomía, Faculdade de Ciências, Universidade do Porto, Portugal 6 SUPA, School of Physics and Astronomy, University of St. Andrews, St. Andrews KY16 9SS, UK Received 28 November 2014 / Accepted 14 December 2014 ABSTRACT Aims. We aim, on the one hand, to study the possible differences of Li abundances between planet hosts and stars without detected planets at effective temperatures hotter than the Sun, and on the other hand, to explore the Li dip and the evolution of Li at high metallicities. Methods. We present lithium abundances for 353 main sequence stars with and without planets in the Teff range 5900–7200 K. We observed 265 stars of our sample with HARPS spectrograph during different planets search programs. We observed the remaining targets with a variety of high-resolution spectrographs.
    [Show full text]
  • Naming the Extrasolar Planets
    Naming the extrasolar planets W. Lyra Max Planck Institute for Astronomy, K¨onigstuhl 17, 69177, Heidelberg, Germany [email protected] Abstract and OGLE-TR-182 b, which does not help educators convey the message that these planets are quite similar to Jupiter. Extrasolar planets are not named and are referred to only In stark contrast, the sentence“planet Apollo is a gas giant by their assigned scientific designation. The reason given like Jupiter” is heavily - yet invisibly - coated with Coper- by the IAU to not name the planets is that it is consid- nicanism. ered impractical as planets are expected to be common. I One reason given by the IAU for not considering naming advance some reasons as to why this logic is flawed, and sug- the extrasolar planets is that it is a task deemed impractical. gest names for the 403 extrasolar planet candidates known One source is quoted as having said “if planets are found to as of Oct 2009. The names follow a scheme of association occur very frequently in the Universe, a system of individual with the constellation that the host star pertains to, and names for planets might well rapidly be found equally im- therefore are mostly drawn from Roman-Greek mythology. practicable as it is for stars, as planet discoveries progress.” Other mythologies may also be used given that a suitable 1. This leads to a second argument. It is indeed impractical association is established. to name all stars. But some stars are named nonetheless. In fact, all other classes of astronomical bodies are named.
    [Show full text]
  • Modeling Radial Velocity Signals for Exoplanet Search Applications
    MODELING RADIAL VELOCITY SIGNALS FOR EXOPLANET SEARCH APPLICATIONS Prabhu Babu∗, Petre Stoica Division of Systems and Control, Department of Information Technology Uppsala University, P.O. Box 337, SE-75 105, Uppsala, Sweden {prabhu.babu, ps}@it.uu.se Jian Li Department of Electrical and Computer Engineering, University of Florida, Gainesville, 32611, FL, U.S.A. [email protected]fl.edu Keywords: Radial velocity method, Exoplanet search, Kepler model, IAA, Periodogram, RELAX, GLRT. Abstract: In this paper, we introduce an estimation technique for analyzing radial velocity data commonly encountered in extrasolar planet detection. We discuss the Keplerian model for radial velocity data measurements and estimate the 3D spectrum (power vs. eccentricity, orbital period and periastron passage time) of the radial velocity data by using a relaxation maximum likelihood algorithm (RELAX). We then establish the significance of the spectral peaks by using a generalized likelihood ratio test (GLRT). Numerical experiments are carried out on a real life data set to evaluate the performance of our method. 1 INTRODUCTION on iterative deconvolution in the frequency domain to obtain a clean spectrum from an initial dirty one. A Extrasolar planet (or shortly exoplanet) detection is periodogram related method is the least squares peri- a fascinating and challenging area of research in the odogram (also called the Lomb-Scargle periodogram) field of astrophysics. Till mid 2009, 353 exoplanets (Lomb, 1976; Scargle, 1982) which estimates the si- have been discovered. Some of the techniques avail- nusoidal components by fitting them to the observed able in the astrophysics literature to detect exoplanets data. Most recently, (Yardibi et al., 2010; Stoica et al., are astrometry, the radial velocity method, pulsar tim- 2009) introduced a new method called the Iterative ing, the transit method and gravitational microlens- Adaptive Approach (IAA), which relies on solving an ing.
    [Show full text]
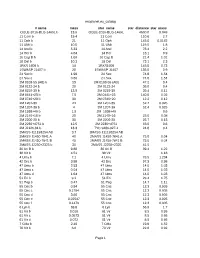
  • Exoplanet.Eu Catalog Page 1 # Name Mass Star Name
    exoplanet.eu_catalog # name mass star_name star_distance star_mass OGLE-2016-BLG-1469L b 13.6 OGLE-2016-BLG-1469L 4500.0 0.048 11 Com b 19.4 11 Com 110.6 2.7 11 Oph b 21 11 Oph 145.0 0.0162 11 UMi b 10.5 11 UMi 119.5 1.8 14 And b 5.33 14 And 76.4 2.2 14 Her b 4.64 14 Her 18.1 0.9 16 Cyg B b 1.68 16 Cyg B 21.4 1.01 18 Del b 10.3 18 Del 73.1 2.3 1RXS 1609 b 14 1RXS1609 145.0 0.73 1SWASP J1407 b 20 1SWASP J1407 133.0 0.9 24 Sex b 1.99 24 Sex 74.8 1.54 24 Sex c 0.86 24 Sex 74.8 1.54 2M 0103-55 (AB) b 13 2M 0103-55 (AB) 47.2 0.4 2M 0122-24 b 20 2M 0122-24 36.0 0.4 2M 0219-39 b 13.9 2M 0219-39 39.4 0.11 2M 0441+23 b 7.5 2M 0441+23 140.0 0.02 2M 0746+20 b 30 2M 0746+20 12.2 0.12 2M 1207-39 24 2M 1207-39 52.4 0.025 2M 1207-39 b 4 2M 1207-39 52.4 0.025 2M 1938+46 b 1.9 2M 1938+46 0.6 2M 2140+16 b 20 2M 2140+16 25.0 0.08 2M 2206-20 b 30 2M 2206-20 26.7 0.13 2M 2236+4751 b 12.5 2M 2236+4751 63.0 0.6 2M J2126-81 b 13.3 TYC 9486-927-1 24.8 0.4 2MASS J11193254 AB 3.7 2MASS J11193254 AB 2MASS J1450-7841 A 40 2MASS J1450-7841 A 75.0 0.04 2MASS J1450-7841 B 40 2MASS J1450-7841 B 75.0 0.04 2MASS J2250+2325 b 30 2MASS J2250+2325 41.5 30 Ari B b 9.88 30 Ari B 39.4 1.22 38 Vir b 4.51 38 Vir 1.18 4 Uma b 7.1 4 Uma 78.5 1.234 42 Dra b 3.88 42 Dra 97.3 0.98 47 Uma b 2.53 47 Uma 14.0 1.03 47 Uma c 0.54 47 Uma 14.0 1.03 47 Uma d 1.64 47 Uma 14.0 1.03 51 Eri b 9.1 51 Eri 29.4 1.75 51 Peg b 0.47 51 Peg 14.7 1.11 55 Cnc b 0.84 55 Cnc 12.3 0.905 55 Cnc c 0.1784 55 Cnc 12.3 0.905 55 Cnc d 3.86 55 Cnc 12.3 0.905 55 Cnc e 0.02547 55 Cnc 12.3 0.905 55 Cnc f 0.1479 55
    [Show full text]
  • IAU Division C Working Group on Star Names 2019 Annual Report
    IAU Division C Working Group on Star Names 2019 Annual Report Eric Mamajek (chair, USA) WG Members: Juan Antonio Belmote Avilés (Spain), Sze-leung Cheung (Thailand), Beatriz García (Argentina), Steven Gullberg (USA), Duane Hamacher (Australia), Susanne M. Hoffmann (Germany), Alejandro López (Argentina), Javier Mejuto (Honduras), Thierry Montmerle (France), Jay Pasachoff (USA), Ian Ridpath (UK), Clive Ruggles (UK), B.S. Shylaja (India), Robert van Gent (Netherlands), Hitoshi Yamaoka (Japan) WG Associates: Danielle Adams (USA), Yunli Shi (China), Doris Vickers (Austria) WGSN Website: https://www.iau.org/science/scientific_bodies/working_groups/280/ ​ WGSN Email: [email protected] ​ The Working Group on Star Names (WGSN) consists of an international group of astronomers with expertise in stellar astronomy, astronomical history, and cultural astronomy who research and catalog proper names for stars for use by the international astronomical community, and also to aid the recognition and preservation of intangible astronomical heritage. The Terms of Reference and membership for WG Star Names (WGSN) are provided at the IAU website: https://www.iau.org/science/scientific_bodies/working_groups/280/. ​ ​ ​ WGSN was re-proposed to Division C and was approved in April 2019 as a functional WG whose scope extends beyond the normal 3-year cycle of IAU working groups. The WGSN was specifically called out on p. 22 of IAU Strategic Plan 2020-2030: “The IAU serves as the ​ internationally recognised authority for assigning designations to celestial bodies and their surface features. To do so, the IAU has a number of Working Groups on various topics, most notably on the nomenclature of small bodies in the Solar System and planetary systems under Division F and on Star Names under Division C.” WGSN continues its long term activity of researching cultural astronomy literature for star names, and researching etymologies with the goal of adding this information to the WGSN’s online materials.
    [Show full text]
  • Mètodes De Detecció I Anàlisi D'exoplanetes
    MÈTODES DE DETECCIÓ I ANÀLISI D’EXOPLANETES Rubén Soussé Villa 2n de Batxillerat Tutora: Dolors Romero IES XXV Olimpíada 13/1/2011 Mètodes de detecció i anàlisi d’exoplanetes . Índex - Introducció ............................................................................................. 5 [ Marc Teòric ] 1. L’Univers ............................................................................................... 6 1.1 Les estrelles .................................................................................. 6 1.1.1 Vida de les estrelles .............................................................. 7 1.1.2 Classes espectrals .................................................................9 1.1.3 Magnitud ........................................................................... 9 1.2 Sistemes planetaris: El Sistema Solar .............................................. 10 1.2.1 Formació ......................................................................... 11 1.2.2 Planetes .......................................................................... 13 2. Planetes extrasolars ............................................................................ 19 2.1 Denominació .............................................................................. 19 2.2 Història dels exoplanetes .............................................................. 20 2.3 Mètodes per detectar-los i saber-ne les característiques ..................... 26 2.3.1 Oscil·lació Doppler ........................................................... 27 2.3.2 Trànsits
    [Show full text]
  • Exoplanet.Eu Catalog Page 1 Star Distance Star Name Star Mass
    exoplanet.eu_catalog star_distance star_name star_mass Planet name mass 1.3 Proxima Centauri 0.120 Proxima Cen b 0.004 1.3 alpha Cen B 0.934 alf Cen B b 0.004 2.3 WISE 0855-0714 WISE 0855-0714 6.000 2.6 Lalande 21185 0.460 Lalande 21185 b 0.012 3.2 eps Eridani 0.830 eps Eridani b 3.090 3.4 Ross 128 0.168 Ross 128 b 0.004 3.6 GJ 15 A 0.375 GJ 15 A b 0.017 3.6 YZ Cet 0.130 YZ Cet d 0.004 3.6 YZ Cet 0.130 YZ Cet c 0.003 3.6 YZ Cet 0.130 YZ Cet b 0.002 3.6 eps Ind A 0.762 eps Ind A b 2.710 3.7 tau Cet 0.783 tau Cet e 0.012 3.7 tau Cet 0.783 tau Cet f 0.012 3.7 tau Cet 0.783 tau Cet h 0.006 3.7 tau Cet 0.783 tau Cet g 0.006 3.8 GJ 273 0.290 GJ 273 b 0.009 3.8 GJ 273 0.290 GJ 273 c 0.004 3.9 Kapteyn's 0.281 Kapteyn's c 0.022 3.9 Kapteyn's 0.281 Kapteyn's b 0.015 4.3 Wolf 1061 0.250 Wolf 1061 d 0.024 4.3 Wolf 1061 0.250 Wolf 1061 c 0.011 4.3 Wolf 1061 0.250 Wolf 1061 b 0.006 4.5 GJ 687 0.413 GJ 687 b 0.058 4.5 GJ 674 0.350 GJ 674 b 0.040 4.7 GJ 876 0.334 GJ 876 b 1.938 4.7 GJ 876 0.334 GJ 876 c 0.856 4.7 GJ 876 0.334 GJ 876 e 0.045 4.7 GJ 876 0.334 GJ 876 d 0.022 4.9 GJ 832 0.450 GJ 832 b 0.689 4.9 GJ 832 0.450 GJ 832 c 0.016 5.9 GJ 570 ABC 0.802 GJ 570 D 42.500 6.0 SIMP0136+0933 SIMP0136+0933 12.700 6.1 HD 20794 0.813 HD 20794 e 0.015 6.1 HD 20794 0.813 HD 20794 d 0.011 6.1 HD 20794 0.813 HD 20794 b 0.009 6.2 GJ 581 0.310 GJ 581 b 0.050 6.2 GJ 581 0.310 GJ 581 c 0.017 6.2 GJ 581 0.310 GJ 581 e 0.006 6.5 GJ 625 0.300 GJ 625 b 0.010 6.6 HD 219134 HD 219134 h 0.280 6.6 HD 219134 HD 219134 e 0.200 6.6 HD 219134 HD 219134 d 0.067 6.6 HD 219134 HD
    [Show full text]
  • A Bayesian Kepler Periodogram Detects a Second Planet in HD 208487
    Mon. Not. R. Astron. Soc. 000, 1–14 (2006) Printed 20 July 2007 (MN LATEX style file v2.2) A Bayesian Kepler Periodogram Detects a Second Planet in HD 208487 P. C. Gregory1??† 1Physics and Astronomy Department, University of British Columbia, 6224 Agricultural Rd., Vancouver, British Columbia, V6T 1Z1, Canada MNRAS 374, 1321, 2007 (Table 1 typos fixed) ABSTRACT An automatic Bayesian Kepler periodogram has been developed for identifying and characterizing multiple planetary orbits in precision radial velocity data. The peri- odogram is powered by a parallel tempering MCMC algorithm which is capable of efficiently exploring a multi-planet model parameter space. The periodogram employs an alternative method for converting the time of an observation to true anomaly that enables it to handle much larger data sets without a significant increase in compu- tation time. Improvements in the periodogram and further tests using data from HD 82 208487 have resulted in the detection of a second planet with a period of 909−92d, an 0.26 0.13 0.11 eccentricity of 0.37−0.20, a semi-major axis of 1.87−0.14 au and an M sin i =0.45−0.13 MJ. The revised parameters of the first planet are period = 129.8 ± 0.4d, eccentricity =0.20±0.09, semi-major axis = 0.51±0.02 au and M sin i =0.41±0.05 MJ. Particu- lar attention is paid to several methods for calculating the model marginal likelihood which is used to compare the probabilities of models with different numbers of planets. Key words: stars: planetary systems; stars: individual: HD 208487; methods: statis- tical; methods: numerical; techniques: radial velocities.
    [Show full text]
  • About Putative Neptune-Like Extrasolar Planetary Candidates
    Astronomy & Astrophysics manuscript no. ms c ESO 2018 September 28, 2018 About putative Neptune-like extrasolar planetary candidates Krzysztof Go´zdziewski and Cezary Migaszewski Toru´nCentre for Astronomy, PL-87-100 Toru´n, Poland Received; accepted ABSTRACT Context. We re-analyze the precision radial velocity (RV) data of HD 208487, HD 190360, HD 188015 and HD 114729. These stars are supposed to host Jovian companions in long-period orbits. Aims. We test a hypothesis that the residuals of the 1-planet model of the RV or an irregular scatter of the measurements about the synthetic RV curve may be explained by the existence of additional planets in short-period orbits. Methods. We perform a global search for the best fits in the orbital parameters space with genetic algorithms and simplex method. This makes it possible to verify and extend the results obtained with an application of commonly used FFT-based periodogram analysis for identifying the leading periods. Results. Our analysis confirms the presence of a periodic component in the RV of HD 190360 which may correspond to a hot-Neptune planet. We found four new cases when the 2-planet model yields significantly better fits to the RV data than the best 1-planet solutions. If the periodic variability of the residuals of single-planet fits has indeed a planetary origin then hot-Neptune planets may exist in these extrasolar systems. We estimate their orbital periods in the range of 7–20 d and minimal masses about of 20 masses od the Earth. Key words. extrasolar planets—Doppler technique— HD 208487—HD 190360—HD 188015—HD 114729—HD 147513 1.
    [Show full text]
  • Determining the True Mass of Radial-Velocity Exoplanets with Gaia 9 Planet Candidates in the Brown-Dwarf/Stellar Regime and 27 Confirmed Planets
    Astronomy & Astrophysics manuscript no. exoplanet_mass_gaia c ESO 2020 September 30, 2020 Determining the true mass of radial-velocity exoplanets with Gaia 9 planet candidates in the brown-dwarf/stellar regime and 27 confirmed planets F. Kiefer1; 2, G. Hébrard1; 3, A. Lecavelier des Etangs1, E. Martioli1; 4, S. Dalal1, and A. Vidal-Madjar1 1 Institut d’Astrophysique de Paris, Sorbonne Université, CNRS, UMR 7095, 98 bis bd Arago, 75014 Paris, France 2 LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris, 5 place Jules Janssen, 92195 Meudon, France? 3 Observatoire de Haute-Provence, CNRS, Universiteé d’Aix-Marseille, 04870 Saint-Michel-l’Observatoire, France 4 Laboratório Nacional de Astrofísica, Rua Estados Unidos 154, 37504-364, Itajubá - MG, Brazil Submitted on 2020/08/20 ; Accepted for publication on 2020/09/24 ABSTRACT Mass is one of the most important parameters for determining the true nature of an astronomical object. Yet, many published exoplan- ets lack a measurement of their true mass, in particular those detected thanks to radial velocity (RV) variations of their host star. For those, only the minimum mass, or m sin i, is known, owing to the insensitivity of RVs to the inclination of the detected orbit compared to the plane-of-the-sky. The mass that is given in database is generally that of an assumed edge-on system (∼90◦), but many other inclinations are possible, even extreme values closer to 0◦ (face-on). In such case, the mass of the published object could be strongly underestimated by up to two orders of magnitude.
    [Show full text]
  • Solar System Analogues Among Exoplanetary Systems
    Solar System analogues among exoplanetary systems Maria Lomaeva Lund Observatory Lund University ´´ 2016-EXA105 Degree project of 15 higher education credits June 2016 Supervisor: Piero Ranalli Lund Observatory Box 43 SE-221 00 Lund Sweden Populärvetenskaplig sammanfattning Människans intresse för rymden har alltid varit stort. Man har antagit att andra plan- etsystem, om de existerar, ser ut som vårt: med mindre stenplaneter i banor närmast stjärnan och gas- samt isjättar i de yttre banorna. Idag känner man till drygt 2 000 exoplaneter, d.v.s., planeter som kretsar kring andra stjärnor än solen. Man vet även att vissa av dem saknar motsvarighet i solsystemet, t. ex., heta jupitrar (gasjättar som har migrerat inåt och kretsar väldigt nära stjärnan) och superjordar (stenplaneter större än jorden). Därför blir frågan om hur unikt solsystemet är ännu mer intressant, vilket vi försöker ta reda på i det här projektet. Det finns olika sätt att detektera exoplaneter på men två av dem har gett flest resultat: transitmetoden och dopplerspektroskopin. Med transitmetoden mäter man minsknin- gen av en stjärnas ljus när en planet passerar framför den. Den metoden passar bäst för stora planeter med små omloppsbanor. Dopplerspektroskopin använder sig av Doppler effekten som innebär att ljuset utsänt från en stjärna verkar blåare respektive rödare när en stjärna förflyttar sig fram och tillbaka från observatören. Denna rörelse avslöjar att det finns en planet som kretsar kring stjärnan och påverkar den med sin gravita- tion. Dopplerspektroskopin är lämpligast för massiva planeter med små omloppsbanor. Under projektets gång har vi inte bara letat efter solsystemets motsvarigheter utan även studerat planetsystem som är annorlunda.
    [Show full text]