DOCSLIB.ORG

Structural Characteristics of Gas Hydrates Within the Framework of Generalized Crystallography A

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Structural Characteristics of Gas Hydrates Within the Framework of Generalized Crystallography A Crystallography Reports, Vol. 48, No. 3, 2003, pp. 347–350. Translated from Kristallografiya, Vol. 48, No. 3, 2003, pp. 391–394. Original Russian Text Copyright © 2003 by Talis. THEORY OF CRYSTAL STRUCTURES Structural Characteristics of Gas Hydrates within the Framework of Generalized Crystallography A. L. Talis Russian Institute of Synthesis of Mineral Raw Materials, Aleksandrov, Vladimir oblast, 601650 Russia e-mail: [email protected] Received September 16, 2002 Abstract—It is shown that the symmetry of the {5, 3, 3} polytope (four-dimensional dodecahedron) embedded into E4 enables one to derive all the polyhedra–cavities that make up gas hydrates from the {5, 3} dodecahedron. Consideration is given to the allomorphic embedding of the {5, 3} subgraph into the incidence graph of the Desargues configuration 103, which determines the mechanism of incorporation of guest molecules into the polyhedra–cavities of gas hydrates and their escape from these polyhedra at the symmetry level. The relation- ships obtained may be considered as a basis for an a priori derivation of the determined (periodic and aperiodic) structures of gas hydrates. © 2003 MAIK “Nauka/Interperiodica”. The impossibility of dividing the three-dimensional pentagonal “cap” of the icosahedron into a hexagonal Euclidean space E3 into regular tetrahedra determines 2π one (if a wedge with an angle ------ is inserted), with the the structural characteristics of tetrahedrally coordi- 5 nated aqueous frameworks of gas hydrates that cannot disclination interactions being determined by the prod- be adequately reflected within the framework of classi- uct of the corresponding elements of group Y'. The cal crystallography. For example, the polyhedra–cavi- 2π introduction of two, three, and four Ð------ disclinations ties D, T, P, and H (dodecahedron, tetra-, penta-, and 5 hexadecahedra), the constituent fragments of the struc- into an icosahedron along its fivefold axes results in the tures of gas hydrates, are determined as dual to the Z12, formation of the Z14, Z15, and Z16 polyhedra [2]. Z14, Z15, and Z16 polyhedra (icosahedron and Frank– Kasper polyhedra) [1, 2]; the D' and E polyhedra–cavi- The introduction of a disclination quadruplet (con- 2π 2π ties (Fig. 1) have not been determined as yet [3]. The sisting of two Ð------ and two ------ disclinations) into the symmetry basis of the structural mechanism of the 5 5 incorporation of guest molecules into polyhedra–cavi- vertices of a “rhombus” built by two neighboring trian- ties and their escape from these cavities is also gular faces of the icosahedron results in the flipping of unknown. Below, we show that the specific structural the diagonal in this rhombus (Fig. 1). To the quadruplet features of gas hydrates can be adequately described q or the disclination 2π there corresponds the element only within the framework of the generalized crystal- y(n, 2π) = Ð1 of group Y' and the rotation by 2π along lography [4–7]. the Möbius band [6]. Thus, introducing three 2π discli- nations into the icosahedron (which preserve the sub- The division into regular tetrahedra that are impos- group C3 of its group Yh) and demanding the maximum sible in E3 can be made in a four-dimensional icosahe- point symmetry, we arrive at the twelve-vertex polyhe- dron–polytope {3, 3, 5} whose 120 vertices belong to 3q 3 6 3 dron Z12 /D3h = [4 , 5 , 6 ] with the symmetry group the three-dimensional sphere S3 embedded into E4. The D3h and twenty triangular faces. In this case, four edges {3, 3, 5} polytope and the dual {5, 3, 3} polytope (four- meet at three vertices Z123q/D , five edges at six verti- dimensional dodecahedron) are mapped onto them- 3h ces, and six edges at three vertices; a polyhedron dual selves by the group Y' × Y' of order 14 400. If group Y to this polyhedron is the polyhedron–cavity D' (Fig. 1). of icosahedron rotation consists of 60 g n ϕ elements, ( , ) Along each of the three straight lines connecting pairs where n is the unit vector directed along the icosahe- ϕ of the vertices of the upper and lower hexagonal caps in dron axis around which the rotation by an angle takes π ϕ ϕ 2d 12 2 −2 place, then group Y' consists of 120 y(n, ) and y(n, + Z14 = Z12 /D6d = [5 , 6 ], one may introduce two ------ . 2π) = Ðy(n, ϕ) elements uniquely corresponding to ±ϕ 5 π disclinations rearrange the diagonals of three tet- disclinations introduced into the icosahedron along the 2 ragons consisting of halves of the triangular faces. As a 2π vector n. For example, the element y n, Ð------ corre- result, a 20-vertex polyhedron Z146d, 3q/D = 5 6h (Z122d)6d, 3q/D = [512, 68] is formed, to which the 2π 6h sponds to the disclination Ð------ , which transforms the polyhedron–cavity E is dual (Fig. 1). 5 1063-7745/03/4803-0347 $24.00 © 2003 MAIK “Nauka/Interperiodica” 348 TALIS 1 q 4 3 2 q q q 2* 3* 4* q 1* 3q 3 6 3 6d, 3q 12 8 Z12 /D3h = [4 , 5 , 6 ] Z14 /D6h = [5 , 6 ] D' E 3q 6d, 3q Fig. 1. Graphs of the Z12 /D3h and Z14 /D6h polyhedra and the dual polyhedra–cavities D' and E. The vertices where six edges meet are indicated by filled circles; the vertices where four edges meet, by open squares; the 2π disclination is denoted by letter q in the center of a tetragon, where this disclination can reject and introduce edges shown by dashed and double lines, respectively. 6d, 3q Some of the “back lines” in Z14 /D6h are not shown, the filled vertices in its “equatorial belt” arise due to the introduction of 2π − ------ disclinations along the straight lines 22*, 33*, and 44* in Z14. 5 3q 3 6 In fact, the polyhedron symbols Z12 /D3h = [4 , 5 , into a tetrahedrally coordinated 20-vertex cluster with 3 2d 6d, 3q 12 8 equal edges that leaves no space for a guest molecule. 6 ] and (Z12 ) /D6h = [5 , 6 ] set the disclinations and the corresponding elements of group Y', which A dodecahedron is a {5, 3} map on a sphere (at each determine the derivation of these polyhedra from the vertex, three pentagons meet); its Petrie polygon is a icosahedron. The symmetry of the dual polyhedron is decacycle—the sequence of edges in which each two the same as the symmetry of the initial one, and, there- (and not three) edges belong to one face [7]. Six such fore, all the polyhedra–cavities D', T, P, H, and E can decacycles contain all 30 edges and 20 vertices of the be derived from the dodecahedron D (with the symme- dodecahedron and are isomorphous to the {10, 3}5 map 2π try group Y ) using the Ð------ and 2π disclinations, whose on the nonoriented surface (at each vertex, three deca- h 5 cycles meet, the vertices separated by five edges of Pet- interaction is determined by the products of the corre- rie’s polygon are considered to be equivalent) [8]. The sponding elements of Y'. {10, 3}5 map also contains pentacycles, which are its minimum cycles (Fig. 2a). It is possible to consider as an energetically favor- able transformation such a transformation of the cluster The {10, 3} map is allomorphic to the {10, 3}' that would keep the maximum subgraph containing all 5 5 map (Fig. 2b) and differs from the latter only in its min- its vertices, with all the other conditions being the imum cycles—hexacycles [8]. The transition from same. Since the polyhedra–cavities are derived from π the dodecahedron, the symmetry basis of the structural {10, 3}5 to {10, 3}5' and back is provided by 2 discli- mechanism of incorporation of guest molecules into a nations. Thus, if, for example, in the decacycle polyhedron–cavity (and escape from it) can be deter- 13'65'21'36'74' (the primed figures numerate black ver- mined from the transformation of the dodecahedron tices) divided into four pentacycles the edge 8'10 is CRYSTALLOGRAPHY REPORTS Vol. 48 No. 3 2003 STRUCTURAL CHARACTERISTICS OF GAS HYDRATES 349 (a) 1 1 2 4 3 4 3 12345678910 1 10 6 10 2 8 7 5 9 7 6 q 3 4 5 6 5 6 9 7 8 10 8 5 6 7 3 4 2 3 2 8 9 1 1 10 (b) {5, 3} Table of incidence {5, 3} 10 9 1 3 4 3 9 8 12345678910 2 1 6 10 8 1 2 4 10 6 3 7 5 4 2 8 5 2 7 5 5 6 6 7 4 7 2 5 7 9 1 8 8 9 4 10 3 6 10 1 3 9 6 6 {103} {10} + {10/3} Table of incidence {103} Fig. 2. Dodecahedron and the allomorphic twenty-vertex diamond cluster, their incidence graphs and corresponding incidence tables: (a) in the bichromatic {5, 3} graph of the dodecahedron, six arrows connect the vertices of the same color; the flipping of the edges by a 2π disclination q results in the appearance of a hexacycle in the decacycle; the incidence table of the {5, 3} graph coincides with the incidence table of the Desargues configuration 103 if six arrows are rejected; (b) a twenty-vertex diamond cluster whose bichromatic graph is embedded into the bichromatic graphs {10} + {10/3} set by the incidence table of the Desargues con- figuration 103. The nondiamond bonds are shown by dashed and dash-dotted lines. The filled circles in the incidence tables corre- spond to the cluster edges; the empty circles correspond to the bonds that are not edges.
Load more

Recommended publications
  • Phase Evolution of Ancient and Historical Ceramics
    EMU Notes in Mineralogy, Vol. 20 (2019), Chapter 6, 233–281 The struggle between thermodynamics and kinetics: Phase evolution of ancient and historical ceramics 1 2 ROBERT B. HEIMANN and MARINO MAGGETTI 1Am Stadtpark 2A, D-02826 Go¨rlitz, Germany [email protected] 2University of Fribourg, Department of Geosciences, Earth Sciences, Chemin du Muse´e 6, CH-1700 Fribourg, Switzerland [email protected] This contribution is dedicated to the memory of Professor Ursula Martius Franklin, a true pioneer of archaeometric research, who passed away at her home in Toronto on July 22, 2016, at the age of 94. Making ceramics by firing of clay is essentially a reversal of the natural weathering process of rocks. Millennia ago, potters invented simple pyrotechnologies to recombine the chemical compounds once separated by weathering in order to obtain what is more or less a rock-like product shaped and decorated according to need and preference. Whereas Nature reconsolidates clays by long-term diagenetic or metamorphic transformation processes, potters exploit a ‘short-cut’ of these processes that affects the state of equilibrium of the system being transformed thermally. This ‘short-cut’ is thought to be akin to the development of mineral-reaction textures resulting from disequilibria established during rapidly heated pyrometamorphic events (Grapes, 2006) involving contact aureoles or reactions with xenoliths. In contrast to most naturally consolidated clays, the solidified rock-like ceramic material inherits non-equilibrium and statistical states best described as ‘frozen-in’. The more or less high temperatures applied to clays during ceramic firing result in a distinct state of sintering that is dependent on the firing temperature, the duration of firing, the firing atmosphere, and the composition and grain-size distribution of the clay.
    [Show full text]
  • Preprint American Mineralogist 407
    This is a preprint, the final version is subject to change, of the American Mineralogist (MSA) Cite as Authors (Year) Title. American Mineralogist, in press. (DOI will not work until issue is live.) DOI: http://dx.doi.org/10.2138/am.2012.4189 7/11 1 Semi-quantitative determination of the Fe/Mg ratio in synthetic cordierite using 2 Raman spectroscopy 3 REVISION 1 4 Authors: Udo Haefeker1, Reinhard Kaindl2, Peter Tropper1 5 6 1Institute of Mineralogy and Petrography, University Innsbruck, Innrain 52, A-6020 7 Innsbruck, Austria. 8 E-mail: [email protected] 9 2Present address: MATERIALS – Institute for Surface Technologies and Photonics, 10 Functional Surfaces, JOANNEUM RESEARCH Forschungsgesellschaft mbH, 11 Leobner Straße 94, A-8712 Niklasdorf, Austria. 12 13 ABSTRACT 14 Investigations of H2O-bearing synthetic well-ordered Mg-Fe-cordierites (XFe = 0-1) 15 with micro-Raman spectroscopy revealed a linear correlation between the Fe/Mg 16 ratio and the position of certain Raman peaks. In the range between 100 and 1250 17 cm-1 all peaks except for three peaks shift towards lower wavenumbers with 18 increasing XFe as a consequence of the substitution of the lighter Mg by the heavier 19 Fe atom on the octahedral sites and the associated structural changes. Selected 20 medium and strong peaks show a shift of 5 to 13 cm-1, respectively. Based on recent 21 quantum-mechanicalPreprint calculations American (Kaindl et al. 2011) Mineralogist these shifts can be attributed to 22 specific vibrational modes in the cordierite structure, thus showing that the Mg-Fe 23 exchange affects the vibrational modes of tetrahedral, octahedral and mixed sites.
    [Show full text]
  • Andalusite and Na- and Li-Rich Cordierite in the La Costa Pluton, Sierras Pampeanas, Argentina: Textural and Chemical Evidence for a Magmatic Origin
    Andalusite and Na- and Li-rich cordierite in the La Costa pluton, Sierras Pampeanas, Argentina: textural and chemical evidence for a magmatic origin Pablo H. Alasino . Juan A. Dahlquist . Carmen Galindo · Cesar Casquet · Julio Saavedra Abstraet The La Costa pluton in the Sierra de Velasco Keywords Andalusite· Na- and Li-rich cormerite . (NW Argentina) consists of S-type granitoids that can be S-type granite . La Costa pluton . Sierras Pampeanas grouped into three igneous facies: the alkali-rich Santa Cruz facies (SCF, Si02 ",67 wt%) mstinguished by the presence of andalusite and Na- and Li-rich cormerite Introduetion (Na20 = 1.55-1.77 wt% and LhO = 0.14---0.66 wt%), the Anillaco facies (Si02 '" 74 wt%) with a significant pro­ Andalusite and cormerite are important and common rock­ portion of Mn-rich garnet, and the Anjullón facies (Si02 forming mineral s in metapelitic rocks and may also be '" 7 5 wt%) with abundant albitic plagioc1ase. The petrog­ abundant in felsic peralurninous igneous rocks such as raphy, mineral chemistry and whole-rock geochemistry of granites, pegmatites, aplites and rhyolites. A fundamental the SCF are compatible with magmatic crystallization of question conceming the presence of andalusite and corm­ Na- and Li-rich cormerite, andalusite and muscovite from erite in peraluminous rocks is how they formed, i.e. whe­ the peraluminous magma under moderate P-T conditions ther they crystallized from the magma or were trapped as ('" 1.9 kbar and ca. 735°C). The high Li content of cor­ xenocrysts (e.g. Flood and Shaw 1975 ; Clarke et al. 1976, merite in the SCF is unusual for granitic rocks of inter­ 2005; Bellido and Barrera 1979; Phillips et al.
    [Show full text]
  • Mid-Infrared (2.1-25 Urn) Spectra of Minerals: First Edition
    DEPARTMENT OF THE INTERIOR U.S. GEOLOGICAL SURVEY Mid-Infrared (2.1-25 urn) Spectra of Minerals: First Edition by John W. Salisbury . U.S. Geological Survey1 Louis S. Walter NASA Goddard Space Flight Center2 Norma Vergo U.S. Geological Survey1 Open-File Report 87-263 This report 1s preliminary and has not been reviewed for conformity with U.S. Geological Survey editorial standards. Stop 927 laboratory for Terrestrial Physics Reston, VA 22092 Greenbelt, MD 20771 Contents 1.0 Abstract 2.0 Introduction 3.0 Experimental Technique 3.1 Sample Acquisition and Preparation 3.2 Sample Characterization 3.3 Acquisition of Spectra 3.4 Data Storage and Retrieval 4.0 Discussion of Spectra 4.1 Major Spectral Features of Minerals 4.2 Effect of Particle Size 4.21 Role of surface and volume scattering 4.22 Changes in spectral contrast 4.23 Transparency peaks 4.24 Christiansen frequency 4.3 Effect of Crystal!ographic Orientation 4.4 Effect of Packing 4.5 Effect of Atmospheric Gases 4.6 Effect of Impurities 4.7 Using Laboratory Spectra to Predict Remote Sensing Measurements 5.0 Acknowledgements 6.0 Appendix 1: Mineral spectra and description sheets are presented in alphabetical order. Minerals are listed alphabetically and by mineral class, subclass and group at the beginning of the appendix. 7.0 Appendix 2. Making a KBr Pellet 1.0 ABSTRACT Almost all libraries of mineral spectra 1n the mid-Infrared are 1n the form of transmittance spectra. Although useful In a laboratory setting, such spectra are of limited benefit for Interpreting remote sensing observations because they do not include the effects of scattering.
    [Show full text]
  • Foitite: Formation During Late Stages of Evolution of Complex Granitic Pegmatites at Dobrá Voda, Czech Republic, and Pala, California, U.S.A
    1399 The Canadian Mineralogist Vol. 38, pp. 1399-1408 (2000) FOITITE: FORMATION DURING LATE STAGES OF EVOLUTION OF COMPLEX GRANITIC PEGMATITES AT DOBRÁ VODA, CZECH REPUBLIC, AND PALA, CALIFORNIA, U.S.A. MILAN NOVÁK§ Department of Mineralogy, Petrology and Geochemistry, Masaryk University, Kotláøská 2, CZ-611 37 Brno, Czech Republic MATTHEW C. TAYLOR¶ Department of Geological Sciences, University of Manitoba, Winnipeg, Manitoba R3T 2N2, Canada ABSTRACT Zoned crystals of tourmaline (elbaite–foitite) were found in pockets of the lepidolite-subtype granitic pegmatites at Dobrá Voda, western Moravia, Czech Republic, and the White Queen mine, Pala, San Diego County, California. Zoned crystals consist of pale pink, colorless and greenish Fe-poor elbaite, blue, violet or green Fe-rich elbaite, and dark violet to black foitite. Elbaite– foitite is associated with quartz, cookeite, albite and apatite at Dobrá Voda, and with albite, quartz, K-feldspar, beryl, and musco- vite at the White Queen mine. Chemical compositions of foitite and associated Fe-poor to Fe-rich elbaite are similar at both localities, and exhibit an X-site vacancy (≤0.78 apfu, in foitite), and variable amounts of Ca (≤0.05 apfu), Mn (≤0.47 apfu) and F (≤0.75 apfu, in elbaite), in contrast to foitite that in many cases is F-free. Two distinct stages of late Fe-enrichment in tourmaline were recognized, in contrast to Fe-depletion, noted in many granitic pegmatites. The first stage is generally characterized by increasing Fe and Na, and decreasing Al and Li contents; three substages show the following substitutions: (i) R2 (LiAl)–1, NaR2(OH) X ( ⅪAl2O)–1 and (OH) F–1 for elbaite containing <0.3 Fe apfu at Dobrá Voda (R = Fetot + Mn + Mg + Zn); (ii) Na R2(OH) X X ( ⅪAl2O)–1 or NaR ( ⅪAl)–1 and F (OH)–1 for Fe-rich elbaite with 0.5–1.0 Fe apfu; (iii) AlO2 [Li(OH)2]–1 and (OH) F–1, perhaps combined with R2 (LiAl)–1 for Fe-rich elbaite with 1.0–1.3 Fe apfu at the White Queen mine.
    [Show full text]
  • Lithium in Sekaninaite from the Type Localitv, Dolni Bory. Czech Republic
    167 Thz Canadian M incralo gist Vol. 35, pp.1,67-173(1997) LITHIUMIN SEKANINAITEFROM THE TYPE LOCALITV, DOLNIBORY. CZECH REPUBLIC PETR dERNfI anp RON CHAPMAN Departrnentof GeolagicalSciences, University of Manitoba, Winnipeg,Manitoba R3T2N2 WERNERSCHREYER Irutitut fir Mincralogie, Ruh.r-Uni'ttersitiltBoclun D44801 Bochwa Germary LIIISA OTTOLINI AND PIERO BOTTAZZI CNRCentro d.i Studio per la Cristallochimicae la Cristall.ografia I-27100 Pnia ltaly CATIIERINEA. MoCAMMON BayerischzsGeoinstitw, UniversbAtBayreutfu D-95440 Bayreuth. Germany ABSTRACI The (Si,Al)-orderedFe end-memberof the cordieritegroup, sekaninaite, from its type locality at Dohl Bory, CzechRepublic, was analyze4 and found to contain0.04 - 0.2ALi ard0,1.l -0,2-6Na apfu; (Fe + Mn)/(Mg + Fe + 1!tn) (at.) rangesfrom 0.74 to 0.97.Lithium is incorporatedby the substitutionchNavlli0\4gFe)-r . This sekaninaiteis the first memberof the cordieritegroup reportedto have substantialLi but negligible Be. All samplesof Na,Be-, NaJ-i'Be- and Nati-bearing cordierite-sekadnaite examinedto date show a minor deficit in the tetrahedralsite (0,237 in the literature, 0.036 in our data) and a slight excessof channelcations (NaKCa) over the proportion of (BeIi) (at.). The Li-bearing sekaninaitecomes from ralher simple granitic pegmatites,in which the only Li-bearing minerals are rare tiphylite and cookeite.Thus cordierite-groupminerals are crystal- 'Ihis chemicalsinks for U. ffnding stressesthe needto analyzefor tracelight elements,even in mineralsfrom poorly fractionated andrare-element-depleted environnents, provided the crystal chemistryis favorable. Keyvvords:sekaninaite, cordierite group, lithium, beryllium, CzechRepublic. SoMraans Nous avonsanalysd la sekaninalte,p61e ferrifbre ordonn6en Al,Si du groupede la cordi6rite,provenaat de sa localit6 type, i Dolnl Bory, en R6publiqueTch{ue.
    [Show full text]
  • Boromullite, Al9bsi2o19, a New Mineral from Granulite-Facies Metapelites, Mount Stafford, Central Australia: a Natural Analogue of a Synthetic “Boron-Mullite”
    Eur. J. Mineral. Fast Track Article Fast Track DOI: 10.1127/0935-1221/2008/0020-1809 This paper is dedicated to the memory of Werner Schreyer Boromullite, Al9BSi2O19, a new mineral from granulite-facies metapelites, Mount Stafford, central Australia: a natural analogue of a synthetic “boron-mullite” Ian S. BUICK1,Edward S. GREW2,*, Thomas ARMBRUSTER3,Olaf MEDENBACH4,Martin G. YATES2, Gray E. BEBOUT5 and Geoffrey L. CLARKE6 1 Research School of Earth Sciences, The Australian National University, Canberra, ACT 0200, Australia 2 Department of Earth Sciences, University of Maine, 5790 Bryand Research Center, Orono, Maine 04469-5790, USA *Corresponding author, e-mail: [email protected] 3 Institut für Geologie, Gruppe Mineralogie-Kristallographie, Universität Bern, Freiestrasse 3, 3012 Bern, Switzerland 4 Institut für Geowissenschaften/Mineralogie, Ruhr-Universität Bochum, 44780 Bochum, Germany 5 Department of Earth & Environmental Sciences, Lehigh University, 31 Williams Drive, Bethelem, PA 18015, USA 6 School of Geosciences, University of Sydney, NSW 2006, Australia Abstract: Boromullite is a new mineral corresponding to a 1:1 polysome composed of Al5BO9 and Al2SiO5 modu- les. Electron-microprobe analysis of the holotype prism is SiO2 19.01(1.12), TiO2 0.01(0.02), B2O3 6.52(0.75), Al2O3 74.10(0.95), MgO 0.07(0.03), CaO 0.00(0.02), MnO 0.01(0.04), FeO 0.40(0.08), Sum 100.12 wt.%, which gives Mg0.01Fe0.03Al8.88Si1.93B1.14O18.94 (normalised to 12 cations), ideally Al9BSi2O19. Overall, in the type specimen, it ranges in composition from Mg0.01Fe0.03Al8.72Si2.44B0.80O19.20 to Mg0.01Fe0.03Al9.22Si1.38B1.35O18.67.
    [Show full text]
  • Sekaninaite (Fe ; Mg)2Al4si5o18 C 2001 Mineral Data Publishing, Version 1.2 ° Crystal Data: Orthorhombic
    2+ Sekaninaite (Fe ; Mg)2Al4Si5O18 c 2001 Mineral Data Publishing, version 1.2 ° Crystal Data: Orthorhombic. Point Group: 2=m 2=m 2=m: As poorly developed crystals, to 70 cm. Twinning: Commonly twinned on 110 and 310 , simulating hexagonal symmetry. f g f g Physical Properties: Cleavage: 100 , imperfect; parting on 001 . Hardness = 7{7.5 f g f g D(meas.) = 2.76{2.77 D(calc.) = 2.78 Optical Properties: Transparent to translucent. Color: Blue to blue-violet. Luster: Vitreous. Optical Class: Biaxial ({). Pleochroism: X = colorless; Y = blue; Z = pale blue. Orientation: X = c; Y = b; Z = a. Dispersion: r < v; moderate. Absorption: Y > Z > X. ® = 1.561 ¯ = 1.572 ° = 1.576 2V(meas.) = 66± Cell Data: Space Group: Cccm: a = 17.230(5) b = 9.835(3) c = 9.314(3) Z = 4 X-ray Powder Pattern: Doln¶³ Bory, Czech Republic. 8.583 (100), 3.386 (100), 3.376 (100), 4.081 (83), 3.076 (74), 3.143 (64), 3.043 (57) Chemistry: (1) SiO2 45.10 TiO2 0.04 Al2O3 30.63 Fe2O3 0.91 FeO 17.85 MnO 0.92 MgO 1.69 CaO 0.39 Na2O 0.68 K2O 0.03 + H2O 1.84 H2O¡ 0.12 Total 100.20 2+ (1) Doln¶³ Bory, Czech Republic; corresponding to (Fe1:63Mg0:28Na0:14Mn0:09Ca0:05)§=2:19 3+ (Al3:94Fe0:08)§=4:02Si4:93O18 ² 0:67H2O: Polymorphism & Series: Forms a series with cordierite. Occurrence: In the albite zone of pegmatites in granulites and gneisses (Doln¶³ Bory, Czech Republic); in bauxitic lithomarge intensely altered by a diabase plug (Brockley, Ireland).
    [Show full text]
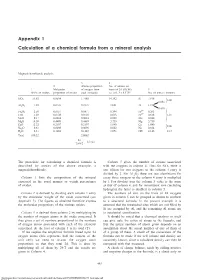
  • Appendix 1 Calculation of a Chemical Formula from a Mineral Analysis
    Appendix 1 Calculation of a chemical formula from a mineral analysis Appendix 1 Magnesiohornblende analysis 3 4 2 Atomic proportion No. of anions on 1 Molecular of oxygen from basis of 24 (O,OH) 5 Wt.% of oxides proportion of oxides each molecule i.e. col. 368.3735 No. of ions in formula SiO 51.63 0.8594 1.7188 14.392 Si 7.196 2 8.00 0.804 } Al2O3 7.39 0.0725 0.2175 1.821 Al 1.214 0.410 3+ Fe2O3 2.50 0.0157 0.0471 0.394 Fe 0.263 FeO 5.30 0.0738 0.0738 0.618 Fe2+ 0.618 5.07 MnO 0.17 0.0024 0.0024 0.020 Mn 0.020 } MgO 18.09 0.4489 0.4489 3.759 Mg 3.759 CaO 12.32 0.2197 0.2197 1.840 Ca 1.840 2.00 Na2O 0.61 0.0098 0.0098 0.082 Na 0.164 } H2O+ 2.31 0.1282 0.1282 1.073 OH 2.146 2.15 Total 100.32 2.8662 24 = 8.3735 2.8662 The procedure for calculating a chemical formula is Column 5 gives the number of cations associated described by means of the above example, a with the oxygens in column 4. Thus for SiO2 there is magnesiohornblende. one silicon for two oxygens so the column 4 entry is divided by 2. For A12O3 there are two aluminiums for Column 1 lists the composition of the mineral every three oxygens so the column 4 entry is multiplied expressed in the usual manner as weight percentages by ~˜.
    [Show full text]
  • Characterization of Low-Temperature Coal Ash Behaviors at High Temperatures Under Reducing Atmosphere
    Available online at www.sciencedirect.com Fuel 87 (2008) 583–591 www.fuelfirst.com Characterization of low-temperature coal ash behaviors at high temperatures under reducing atmosphere Jin Bai a,b, Wen Li a,*, Baoqing Li a a State Key Laboratory of Coal Conversion, Institute of Coal Chemistry, Chinese Academy of Sciences, Taiyuan, 030001, China b Graduate University of Chinese Academy of Sciences, Beijing 100039, China Received 23 November 2006; received in revised form 12 January 2007; accepted 7 February 2007 Available online 9 March 2007 Abstract The coal ash obtained at 815 °C under oxidizing atmosphere was further treated at 1300 °C and 1400 °C under reducing atmosphere. The resultant ashes were examined by XRD, SEM/EDX and FTIR. The results show that the residence time of coal ash at high tem- peratures has considerable influences on the compositions of coal ash and little effect on the amounts of unburned carbon. The amor- phous phase of mineral matters increases with the increasing temperature. The FTIR peaks due to presence of different functional groups of minerals support the findings of XRD, and supply additional information of amorphous phase which cannot be detected in XRD. The ash samples generated from a fixed bed reactor during char gasification were also studied with FTIR. The temperatures of char prep- aration are responsible for the different transformation of minerals during high temperature gasification. Ó 2007 Elsevier Ltd. All rights reserved. Keywords: Coal ash; High temperature; Residence time 1. Introduction transformation under oxidizing and reducing atmospheres. They found that the ash melting behavior was controlled Coal consists of organic components and a range of by iron rich corner in a reducing atmosphere.
    [Show full text]
  • List of Mineral Symbols
    THE CANADIAN MINERALOGIST LIST OF SYMBOLS FOR ROCK- AND ORE-FORMING MINERALS (January 1, 2021) ____________________________________________________________________________________________________________ Ac acanthite Ado andorite Asp aspidolite Btr berthierite Act actinolite Adr andradite Ast astrophyllite Brl beryl Ae aegirine Ang angelaite At atokite Bll beryllonite AeAu aegirine-augite Agl anglesite Au gold Brz berzelianite Aen aenigmatite Anh anhydrite Aul augelite Bet betafite Aes aeschynite-(Y) Ani anilite Aug augite Bkh betekhtinite Aik aikinite Ank ankerite Aur auricupride Bdt beudantite Akg akaganeite Ann annite Aus aurostibite Beu beusite Ak åkermanite An anorthite Aut autunite Bch bicchulite Ala alabandite Anr anorthoclase Aw awaruite Bt biotite* Ab albite Atg antigorite Axn axinite-(Mn) Bsm bismite Alg algodonite Sb antimony Azu azurite Bi bismuth All allactite Ath anthophyllite Bdl baddeleyite Bmt bismuthinite Aln allanite Ap apatite* Bns banalsite Bod bohdanowiczite Alo alloclasite Arg aragonite Bbs barbosalite Bhm böhmite Ald alluaudite Ara aramayoite Brr barrerite Bor boralsilite Alm almandine Arf arfvedsonite Brs barroisite Bn bornite Alr almarudite Ard argentodufrénoysite Blt barylite Bou boulangerite Als alstonite Apn argentopentlandite Bsl barysilite Bnn bournonite Alt altaite Arp argentopyrite Brt baryte, barite Bow bowieite Aln alunite Agt argutite Bcl barytocalcite Brg braggite Alu alunogen Agy argyrodite Bss bassanite Brn brannerite Amb amblygonite Arm armangite Bsn bastnäsite Bra brannockite Ams amesite As arsenic
    [Show full text]
  • Petrologie a Mineralogie Porcelanitů Mostecké Pánve - Produktů Fosilních Požárů Neogénní Hnědouhelné Sloje
    Bull. mineral.-petrolog. Odd. Nár. Muz. (Praha) 18/1, 2010. ISSN: 1211-0329 Petrologie a mineralogie porcelanitů mostecké pánve - produktů fosilních požárů neogénní hnědouhelné sloje Rocks and minerals formed by fossil combustion pyrometamorphism in the Neogene brown coal Most Basin, Czech Republic Vladimír Žáček1), roman Skála2),3) a Zdeněk dVořák4) 1)Česká geologická služba, Klárov 3, 118 21 Praha 1 2)Geologický ústav AV ČR, v.v.i., Rozvojová 269, 165 00 Praha 6 3)Ústav geochemie, mineralogie a nerostných zdrojů, PřF UK, Albertov 6, 128 43 Praha 2 4)Doly Bílina, ul. 5. května 213, 418 29 Bílina Žáček V., Skála r., dVořák Z. (2010): Petrologie a mineralogie porcelanitů mostecké pánve - produktů fosilních požárů neogénní hnědouhelné sloje. - Bull. mineral.-petrolog. Odd. Nár. Muz. (Praha) 8/, 1-32. ISSN: 1211-0329. Abstract Porcellanite is a term conventionally used for multicoloured jasper-like rocks, formed from clays by pyrometamor- phism. In the territory of the Most Basin, however, all pyrometamorphic rocks produced by natural fossil combustion of a Neogene coal seam are traditionally marked by the term „porcellanites“. The Most Basin (also known as the North Bohemian brown-coal Basin) is situated in the northwest of the Czech Republic and with the annual production of ca 50 millions metric tons of brown coal represents the main energy source of the Czech Republic. The previous authors mentioned 65 localities of combustion pyrometamorphic rocks scattered in the region of the Most Basin in the territory of about 1400 km2. The pyrometamorphic complexes form flat-lying or shallow-dipping deposits and they have size ranging from several hundreds metres up to several kilometres and the thickness varying from several metres up to about 35 m.
    [Show full text]