The Optimal Location of Ambulance Stations in a Regional Area: the Case of Mackay
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

West Mackay Growth Profile
West Mackay Growth Profile West Mackay is part of the traditional lands of the Yuwibara people. West Mackay developed along the Bruce Highway as the main transport axis into Mackay. Notable early developments include a government sugar nursery built in 1890 near the lagoons (now the Mackay Botanic Gardens), later replaced by a Sugar Experimental Station in 1898 and the Queensland Heritage listed Sugar Research Institute in 1953 designed by prominent architect Karl Langer. Additionally, the Mackay District Hospital (now the Mackay Base Hospital) was built in 1885 and underwent a series of major expansions in the 1920’s, 1980 and a major redevelopment to its current modern standard between 2010 to 2014. Outlook If current housing trends continue an increase in higher density dwellings and supporting rental housing for local residents. The ageing population trend is anticipated to lead to a greater concentration of empty nesters/retirees in West Mackay. Growth is driven by densification of housing in an older character neighbourhood in close proximity to local employment. Health is anticipated to continue to be a main employer with the location of the Mackay Base Hospital in West Mackay. Total Residents Main Industries of Employment for Residents 2018 2018 Population by Age Dwelling Types West Mackay Growth Profile Demographic Profile 6,124 people live in West Mackay. This represents The age composition has tended more to residents 5.1% of the total population of Mackay region. aged 65+ (19.2% of the population compared to the Mackay region average of 13.1%. ). This is a consistent trend for older suburbs of Mackay region. -
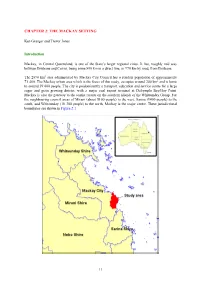
Chapter 2: the Mackay Setting
CHAPTER 2: THE MACKAY SETTING Ken Granger and Trevor Jones Introduction Mackay, in Central Queensland, is one of the State’s larger regional cities. It lies, roughly mid way between Brisbane and Cairns, being some 800 km in a direct line, or 970 km by road, from Brisbane. The 2890 km2 area administered by Mackay City Council has a resident population of approximately 71 400. The Mackay urban area which is the focus of this study, occupies around 240 km2 and is home to around 59 000 people. The city is predominantly a transport, education and service centre for a large sugar and grain growing district, with a major coal export terminal at Dalrymple Bay/Hay Point. Mackay is also the gateway to the tourist resorts on the southern islands of the Whitsunday Group. For the neighbouring council areas of Mirani (about 5100 people) to the west, Sarina (9400 people) to the south, and Whitsunday (18 300 people) to the north, Mackay is the major centre. These jurisdictional boundaries are shown in Figure 2.1. 11 Figure 2.1: Mackay study area location The Physical Setting Topography: The entire study area is low-lying, with an average elevation of less than 10 m above the Australian Height Datum (AHD), with the low hills of Mount Bassett (approximately 30 m above AHD) and Mount Pleasant (about 60 m above AHD) as the main features of relief. In the original area of urban development, south of the Pioneer River, the average elevation is around 6 m above AHD and ranges from less than 4 m above AHD at the airport to a little over 11 m above AHD at the Mackay Base Hospital. -

DIVISION FINDER 2019 Division Finder
2019 COMMONWEALTH OF AUSTRALIA 2019 DIVISION FINDER Division Finder Queensland QLD EF54 EF54 i © Commonwealth of Australia 2019 This work is copyright. All rights reserved. No part of this publication may be reproduced by any means, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, scanning, recording or otherwise, without the written consent of the Australian Electoral Commission. All enquiries should be directed to the Australian Electoral Commission, Locked Bag 4007, Canberra ACT 2601. ii iii Contents Instructions For Use And Other Information Pages v-xiii INTRODUCTION Detailed instructions on how to use the various sections of the Division Finder. DIVISIONAL OFFICES A list of all divisional offices within the State showing physical and postal addresses, and telephone and facsimile numbers. INSTITUTIONS AND ESTABLISHMENTS A list of places of residence such as Universities, Hospitals, Defence Bases and Caravan Parks. This list may be of assistance in identifying institutions or establishments that cannot be found using the Locality and Street Sections. Locality Section Pages 1-43 This section lists all of the suburbs, towns and localities within the State of Queensland and the name of the corresponding electoral division the locality is contained in, or the reference ... See Street Section. Street Section Pages 47-135 This section lists all the streets for those localities in the Locality Section which have the reference ... See Street Section. Each street listing shows the electoral division the street is contained in. iv v Introduction The Division Finder is the official list used to Electors often do not know the correct identify the federal electoral division of the federal division in which they are enrolled, place an elector claims to be enrolled at. -

Seasonal Buyer's Guide
Seasonal Buyer’s Guide. Appendix Queensland Suburb table - May 2017 Westpac, National suburb level appendix Copyright Notice Copyright © 2017CoreLogic Ownership of copyright We own the copyright in: (a) this Report; and (b) the material in this Report Copyright licence We grant to you a worldwide, non-exclusive, royalty-free, revocable licence to: (a) download this Report from the website on a computer or mobile device via a web browser; (b) copy and store this Report for your own use; and (c) print pages from this Report for your own use. We do not grant you any other rights in relation to this Report or the material on this website. In other words, all other rights are reserved. For the avoidance of doubt, you must not adapt, edit, change, transform, publish, republish, distribute, redistribute, broadcast, rebroadcast, or show or play in public this website or the material on this website (in any form or media) without our prior written permission. Permissions You may request permission to use the copyright materials in this Report by writing to the Company Secretary, Level 21, 2 Market Street, Sydney, NSW 2000. Enforcement of copyright We take the protection of our copyright very seriously. If we discover that you have used our copyright materials in contravention of the licence above, we may bring legal proceedings against you, seeking monetary damages and/or an injunction to stop you using those materials. You could also be ordered to pay legal costs. If you become aware of any use of our copyright materials that contravenes or may contravene the licence above, please report this in writing to the Company Secretary, Level 21, 2 Market Street, Sydney NSW 2000. -

Economic Development and Planning Standing Committee Final Minutes
ECONOMIC DEVELOPMENT AND PLANNING STANDING COMMITTEE FINAL MINUTES 10 May 2017 FINAL MINUTES ECONOMIC DEVELOPMENT AND PLANNING STANDING COMMITTEE WEDNESDAY 10 MAY 2017 Table of Contents Folio Date Particulars 43830 10.05.2017 Economic Development and Planning Standing Committee Minutes 43849 30.04.2017 Development Services Monthly Review - April 2017 43864 07.04.2017 Minutes - Character and Heritage Advisory Committee Meeting Declaration of Potential Conflict of Interest Nil. MIN/10.05.2017 FOLIO 43829 FINAL MINUTES ECONOMIC DEVELOPMENT AND PLANNING STANDING COMMITTEE WEDNESDAY 10 MAY 2017 ECONOMIC DEVELOPMENT AND PLANNING STANDING COMMITTEE MINUTES The Chair welcomed Cr Ellison Sade from the Honiara City Council who was sitting in the Public Gallery for today's meeting. 1. COMMITTEE ATTENDANCE: Crs A J Camm (Chairperson), J F Englert, R C Gee, F A Mann, K L May and Mayor G R Williamson were in attendance at the commencement of the meeting. 2. NON-COMMITTEE ATTENDANCE: Also present were Cr R D Walker, Cr M J Bella, Cr A R Paton, Cr L G Bonaventura, Mr C Doyle (Chief Executive Officer), Mr G Carlyon (Director Development Services) and Mrs M Iliffe (Minute Secretary). The meeting commenced at 1.00 pm. 3. ABSENT ON COUNCIL BUSINESS: Nil 4. APOLOGIES: Nil 5. CONFLICT OF INTEREST: Nil MIN/10.05.2017 FOLIO 43830 FINAL MINUTES ECONOMIC DEVELOPMENT AND PLANNING STANDING COMMITTEE WEDNESDAY 10 MAY 2017 6. CONFIRMATION OF MINUTES: 6.1 ECONOMIC DEVELOPMENT AND PLANNING STANDING COMMITTEE MINUTES - 12 APRIL 2017 THAT the Economic Development and Planning Standing Committee Meeting Minutes held on 12 April 2017 be adopted. -

Download a Copy of the Mackay Regional Profile 2018 (PDF)
DISCLAIMER All figures and data presented in this document are based on data sourced from the Australian Bureau of Statistics (ABS), and other government agencies. Using ABS datasets, the regional economic modelling software ‘REMPLAN Economy’, has been applied to generate industrial economic data estimates. This document is provided in good faith with every effort made to provide accurate data and apply comprehensive knowledge. However, REMPLAN does not guarantee the accuracy of data nor the conclusions drawn from this information. Economic Development Department (07) 5689 1499 / (03) 5444 4788 1300 MACKAY (622 529) www.remplan.com.au [email protected] www.investmackay.com OVERVIEW EMPLOYMENT DEMOGRAPHICS INDUSTRY HOUSING TRENDS TOURISM RESOURCES The region’s expanding employment, investment and development opportunities, buoyant economy and lifestyle attributes are just some of the many positive aspects that encourage people to live, work and play in the Mackay Region. The Mackay Regional Local Government Area is one of the fastest-growing in Queensland, with a population of 118,000. The region’s growth is fuelled by activity in the resources sector, resurgence in agribusiness, and growth in construction, logistics and tourism. The Mackay Region is the gateway to the rich coal deposits in the Bowen and Galilee Basins. It is one of the largest sugar-producing regions in Australia and hosts much of the engineering, manufacturing and mining services industries supporting the wider Mackay-Isaac-Whitsunday economy. Only an hour’s flight from Brisbane, the Mackay Region boasts an enviable lifestyle and a buoyant economy with the benefits of a fast-growing coastal city. -

Final Minutes
FINAL MINUTES 15 May 2013 FINAL MINUTES WEDNESDAY 15 MAY 2013 Table of Contents Folio Date Particulars 27327 15.05.2013 Ordinary Meeting Minutes 27363 30.04.2013 Community Services Monthly Review for April 2013 27402 15.05.2013 MRC Policy Review Project: Use of the Bluewater Lagoon 27404 30.04.2013 Development Services Highlights & Significant Issues Report for April 2013 27456 15.05.2013 2012/2013 Operational Plan - Third Quarter Review 27526 18.04.2013 Minutes - Rural Affairs Advisory Committee 27533 12.04.2013 Minutes - Character Heritage Advisory Committee 27538 06.05.2013 Minutes - Sustainable Futures Advisory Committee Declaration of Potential Conflict of Interest Nil. MIN/15.05.2013 FOLIO 27326 FINAL MINUTES WEDNESDAY 15 MAY 2013 ORDINARY MEETING MINUTES 1. ATTENDANCE: Her Worship the Mayor, Cr D T Comerford (Chairperson), Crs K J Casey, C J Bonanno, L G Bonaventura, F A Gilbert, A N Jones, G J Martin, T A Morgan, D J Perkins, P F Steindl, and R D Walker were in attendance at the commencement of the meeting. Also present was Mr B Omundson (Chief Executive Officer) and Mrs M Iliffe (Minute Secretary). The meeting commenced at 10.00 am. 2. ABSENT ON COUNCIL BUSINESS: Nil 3. APOLOGIES: Nil 4. CONDOLENCES: Nil 5. CONFIRMATION OF MINUTES: 5.1 ORDINARY MEETING MINUTES 1 MAY 2013 THAT the Minutes of the Ordinary Meeting held on 1 May 2013 be confirmed. Moved Cr Casey Seconded Cr Bonaventura CARRIED MIN/15.05.2013 FOLIO 27327 FINAL MINUTES WEDNESDAY 15 MAY 2013 6. BUSINESS ARISING OUT OF MINUTES OF PREVIOUS MEETING: Nil 7. -

West Mackay Drainage Study
Mackay Regional Council 11-Sep-2019 Doc No. M031-19 West Mackay Drainage Study Volume 1 Report Revision A – 11-Sep-2019 Prepared for – Mackay Regional Council – ABN: 56 240 712 069 AECOM West Mackay Drainage Study – Volume 1 Report West Mackay Drainage Study Volume 1 Report Client: Mackay Regional Council ABN: 56 240 712 069 Prepared by AECOM Australia Pty Ltd Level 1, 162 Victoria Street, PO Box 11176, Mackay QLD 4740, Australia T +61 7 4965 9800 F +61 7 4957 6097 www.aecom.com ABN 20 093 846 925 11-Sep-2019 Job No.: 60589930 AECOM in Australia and New Zealand is certified to ISO9001, ISO14001 AS/NZS4801 and OHSAS18001. © AECOM Australia Pty Ltd (AECOM). All rights reserved. AECOM has prepared this document for the sole use of the Client and for a specific purpose, each as expressly stated in the document. No other party should rely on this document without the prior written consent of AECOM. AECOM undertakes no duty, nor accepts any responsibility, to any third party who may rely upon or use this document. This document has been prepared based on the Client’s description of its requirements and AECOM’s experience, having regard to assumptions that AECOM can reasonably be expected to make in accordance with sound professional principles. AECOM may also have relied upon information provided by the Client and other third parties to prepare this document, some of which may not have been verified. Subject to the above conditions, this document may be transmitted, reproduced or disseminated only in its entirety. -

Welcome to Mackay
October 2017 WELCOME TO MACKAY We would like to extend to you and your family, a very warm welcome to the city of Mackay and the Isaac Region. Mackay is a great place to live and offers all the conveniences and attractions you would expect to find in such a vibrant city and thriving area. We at Mackay Tourism are only too happy to provide you with all the information you need to find your way around and to help you settle into your new life here. Mackay Tourism is a licensed travel agency. Our Information Centre is open seven days per week and is located at 320 Nebo Road, Mackay – 07 4944 5888 Our friendly efficient staff, are here to assist you in planning any tours, trips and accommodation in the area and throughout Australia. Another fun way to orientate yourself to your surroundings is to become a volunteer with Mackay Tourism. Come in and chat to our happy team. So please, come in! We would love to help you to enjoy all that our beautiful region has to offer. EVERYTHING YOU NEED TO KNOW ABOUT LIVING IN MACKAY… For further information visit our website at www.mackayregion.com or the Mackay Regional Council website at www.mackay.qld.gov.au EMPLOYMENT LABOUR HIRE COMPANY ADDRESS PHONE EMAIL/WEBSITE 4BU Mining Mackay & Bowen Basin 0428 222 546 [email protected] Services All Mine 11 Elvin St, Paget 4952 3033 http://www.allmineservices.com.au Services AWX 97 Victoria St, Mackay 1300 299 299 www.awx.com.au Axial 21 Boundary Rd E, Paget 4963 3700 www.axial.com.au/ 1 Callcorr PTY 7 Munbura Road, Mackay 4959 6211 [email protected] LTD -

Find-Your-Local-Regional-Office.Pdf
Find Your Local Department of Employment, Small Business and Training Office Version 69 September 2021 To find your local department office, select 'Ctrl' and 'F' and search for either the suburb or postcode Or use the search function by right clicking on the document and selecting 'Find' Suburb/Town Postcode Regional Office Email Postal Address Physical Address ABBEYWOOD 4613 Toowoomba [email protected] PO Box 234, TOOWOOMBA QLD 4350 Lvl 1, James Cook Cntr, Cnr Herries & Ruthven St, TOOWOOMBA QLD 4350 Lvl 1, 102 Lennox St, MARYBOROUGH QLD 4650 and DET ABBOTSFORD 4670 Wide Bay [email protected] PO Box 1046, MARYBOROUGH QLD 4650 North Coast Region, Cnr Woondooma & Maryborough St, BUNDABERG QLD 4670 ABERCORN 4627 Gladstone [email protected] 20-22 Herbert St, GLADSTONE QLD 4680 Lvl 1, 20-22 Herbert St, GLADSTONE QLD 4680 ABERGOWRIE 4850 Townsville [email protected] PO Box 2122, TOWNSVILLE QLD 4810 Lvl 1, 187-209 Stanley St, TOWNSVILLE QLD 4810 ABINGDON DOWNS 4892 Cairns [email protected] PO Box 4993, CAIRNS QLD 4870 Ground Fl, State Govt Bldg, 17-19 Sheridan St, CAIRNS QLD 4870 Lvl 1, 102 Lennox St, MARYBOROUGH QLD 4650 and DET ABINGTON 4660 Wide Bay [email protected] PO Box 1046, MARYBOROUGH QLD 4650 North Coast Region, Cnr Woondooma & Maryborough St, BUNDABERG QLD 4670 ACACIA RIDGE 4110 Metro South (Mt Gravatt) [email protected] PO Box 6500, UPPER MT GRAVATT QLD 4122 Lvl 2, Block A, Garden Sq, 643 Kessels Rd, UPPER MT GRAVATT QLD 4122 ACACIA RIDGE -
INDEXED CONTRIBUTION RATES 4 Applicable Relevant Index Policy Applicable Areas Charge Rate 5 Index Value
EFFECTIVE: 01 August 2017- 30 October 2017 MACKAY CITY PLANNING SCHEME - CONTRIBUTION POLICIES - INDEXED CONTRIBUTION RATES 4 Applicable Relevant Index Policy Applicable Areas Charge Rate 5 Index Value RBCI 108.9 16.01 TRANSPORT NETWORK CONTRIBUTIONS POLICY Per VPD 2 Queensland Jun 17 1. Entire City of Mackay………………………………………………………………………………………………………………………………………. $417 CPI All Groups 111.0 16.02 PARKS CONTRIBUTION POLICY - PUBLIC PARKS AND COMMUNITY LAND (PPCL) DEVELOPER CONTRIBUTIONS Per EP 1 Brisbane Jun 17 1. Shoal Point - Bucasia.………………………………………………………………………………………………………………………………………. $1,765 2. Rural View, Eimeo, Blacks Beach, Dolphin Heads.……………………………………………………………………………………………………………………………………….$1,937 3. Mt Pleasant, Glenella, Beaconsfield, Andergrove, North Mackay, Cremorne, Slade Point, Mackay Harbour.……………………………… $1,818 4. City, West Mackay, East Mackay, South Mackay.……………………………………………………………………………………………………………………………………….$1,505 5. Ooralea, Paget.………………………………………………………………………………………………………………………………………. $1,787 6. Walkerston.………………………………………………...…………………………………………………………………………………………………. $1,425 7. Remainder of Scheme Area.……………………………………………………………………………………………………………………………………….$1,705 GCI 3 118.6 16.03 WATER SUPPLY AND SEWERAGE INFRASTRUCTURE CONTRIBUTIONS POLICY Per ET Queensland 2 Jun 17 WATER 1. North Mackay, Andergrove, Beaconsfield, Mount Pleasant, Glenella……………………………………………………………………………………………………$6,017 2. Mackay City (Pioneer River - Archibald Street & Peak Downs Highway)……………………………………………………………………………………………$6,017 3. South Mackay (South of Archibald Street -

My Berries Homedelivery Postcodes
MY BERRIES HOME DELIVERY POSTCODES ABBOTSBURY 2176 NSW ANDERGROVE 4740 QLD AUBURN 2144 NSW ABBOTSFORD 2046 NSW ANDROMACHE 4800 QLD AUCHENFLOWER 4066 QLD ABERDARE 2325 NSW ANGOURIE 2464 NSW AUGUSTINE HEIGHTS 4300 QLD ABERGLASSLYN 2320 NSW ANNA BAY 2316 NSW AUSTRAL 2179 NSW ABERMAIN 2326 NSW ANNANDALE 2038 NSW AUSTRALIA FAIR 4215 QLD ACACIA GARDENS 2763 NSW ANNANGROVE 2156 NSW AVALON 2107 NSW ACACIA RIDGE 4110 QLD ANNERLEY 4103 QLD AVALON BEACH 2107 NSW ACACIA RIDGE BC 4110 QLD ANNERLEY DC 4103 QLD AVENELL HEIGHTS 4670 QLD ACACIA RIDGE DC 4110 QLD ANSTEAD 4070 QLD AVOCA 4670 QLD ACLAND 4401 QLD APPLE TREE CREEK 4660 QLD AVOCA BEACH 2251 NSW ADAMSTOWN 2289 NSW APPLETHORPE 4378 QLD AWABA 2283 NSW ADAMSTOWN HEIGHTS 2289 NSW ARANA HILLS 4054 QLD BADGERYS CREEK 2555 NSW ADARE 4343 QLD ARCADIA 2159 NSW BAGO 2446 NSW AGNES BANKS 2753 NSW ARCADIA VALE 2283 NSW BAGOTVILLE 2477 NSW AIRDS 2560 NSW ARCHERFIELD 4108 QLD BAJOOL 4699 QLD AIRLIE BEACH 4802 QLD ARCHERFIELD BC 4108 QLD BAKERS CREEK 4740 QLD ALBANY CREEK 4035 QLD ARGENTON 2284 NSW BALBERRA 4740 QLD ALBION 4010 QLD ARMIDALE 2350 NSW BALCOLYN 2264 NSW ALBION BC 4010 QLD ARMSTRONG BEACH 4737 QLD BALD HILLS 4036 QLD ALBION DC 4010 QLD ARNCLIFFE 2205 NSW BALGOWLAH 2093 NSW ALDERLEY 4051 QLD ARNDELL PARK 2148 NSW BALGOWLAH HEIGHTS 2093 NSW ALDERSHOT 4650 QLD AROONA 4551 QLD BALL BAY 4741 QLD ALEXANDRA 4740 QLD ARRAWARRA 2456 NSW BALLANDEAN 4382 QLD ALEXANDRA HEADLAND 4572 QLD ARRAWARRA HEADLAND 2456 NSW BALLARD 4352 QLD ALEXANDRA HILLS 4161 QLD ARTARMON 2064 NSW BALLINA 2478 NSW ALEXANDRIA 2015