Verification and Validation in Computational Fluid Dynamics1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle
On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle Agah D. Garnadi 31 December 2017 Department of Mathematics, Faculty of Mathematics and Natural Sciences, Bogor Agricultural University Jl. Meranti, Kampus IPB Darmaga, Bogor, 16680 Indonesia Abstract This note is addressed to solving biperiodic boundary value prob- lem of biharmonic equation in the unit rectangle. First, we describe the necessary tools, which is discrete Fourier transform for one di- mensional periodic sequence, and then extended the results to 2- dimensional biperiodic sequence. Next, we use the discrete Fourier transform 2-dimensional biperiodic sequence to solve discretization of the biperiodic boundary value problem of Biharmonic Equation. MSC: 15A09; 35K35; 41A15; 41A29; 94A12. Key words: Biharmonic equation, biperiodic boundary value problem, discrete Fourier transform, Partial differential equations, Interpola- tion. 1 Introduction This note is an extension of a work by Henrici [2] on fast solver for Poisson equation to biperiodic boundary value problem of biharmonic equation. This 1 note is organized as follows, in the first part we address the tools needed to solve the problem, i.e. introducing discrete Fourier transform (DFT) follows Henrici's work [2]. The second part, we apply the tools already described in the first part to solve discretization of biperiodic boundary value problem of biharmonic equation in the unit rectangle. The need to solve discretization of biharmonic equation is motivated by its occurence in some applications such as elasticity and fluid flows [1, 4], and recently in image inpainting [3]. Note that the work of Henrici [2] on fast solver for biperiodic Poisson equation can be seen as solving harmonic inpainting. -
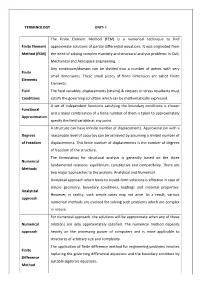
TERMINOLOGY UNIT- I Finite Element Method (FEM)
TERMINOLOGY UNIT- I The Finite Element Method (FEM) is a numerical technique to find Finite Element approximate solutions of partial differential equations. It was originated from Method (FEM) the need of solving complex elasticity and structural analysis problems in Civil, Mechanical and Aerospace engineering. Any continuum/domain can be divided into a number of pieces with very Finite small dimensions. These small pieces of finite dimension are called Finite Elements Elements. Field The field variables, displacements (strains) & stresses or stress resultants must Conditions satisfy the governing condition which can be mathematically expressed. A set of independent functions satisfying the boundary conditions is chosen Functional and a linear combination of a finite number of them is taken to approximately Approximation specify the field variable at any point. A structure can have infinite number of displacements. Approximation with a Degrees reasonable level of accuracy can be achieved by assuming a limited number of of Freedom displacements. This finite number of displacements is the number of degrees of freedom of the structure. The formulation for structural analysis is generally based on the three Numerical fundamental relations: equilibrium, constitutive and compatibility. There are Methods two major approaches to the analysis: Analytical and Numerical. Analytical approach which leads to closed-form solutions is effective in case of simple geometry, boundary conditions, loadings and material properties. Analytical However, in reality, such simple cases may not arise. As a result, various approach numerical methods are evolved for solving such problems which are complex in nature. For numerical approach, the solutions will be approximate when any of these Numerical relations are only approximately satisfied. -

Survey Experiments
IU Workshop in Methods – 2019 Survey Experiments Testing Causality in Diverse Samples Trenton D. Mize Department of Sociology & Advanced Methodologies (AMAP) Purdue University Survey Experiments Page 1 Survey Experiments Page 2 Contents INTRODUCTION ............................................................................................................................................................................ 8 Overview .............................................................................................................................................................................. 8 What is a survey experiment? .................................................................................................................................... 9 What is an experiment?.............................................................................................................................................. 10 Independent and dependent variables ................................................................................................................. 11 Experimental Conditions ............................................................................................................................................. 12 WHY CONDUCT A SURVEY EXPERIMENT? ........................................................................................................................... 13 Internal, external, and construct validity .......................................................................................................... -

Team Photo/History Team Team Photo/History Team
TEAM PHOTO/HISTORY TEAM PHOTO/HISTORY TEAM PHOTO/HISTORY TEAM PHOTO/HISTORY TEAM PHOTO/HISTORY Team Photo The 2003-04 Utes, Front Row: Alpine Coach Aaron Atkins, Casey Simons, Ashley McQueen, Lauren Lattimer, Lina Johansson, Jenny Hansson, Anna Sprague, Barbro Hatlevik. Middle Row: Student Assistant Kristian Guay, Assistant Cross Country Coach Petter Svendsen, Sandra Gredig, Elisha Stephens, Rowena Hyldahl, Linda Pettersson, Student-Assistant Katrin Smigun, Assistant Alpine Coach Jaka Korencan, Gaspar Perricone. Back Row: Head Coach Kevin Sweeney, Athletics Trainer Bob Toth, Henning Dybendal, Tony Bozzio, Jess Kiesel, Will McDonald, Andi Weiser, Ben Thornhill, Pierre Olsson, Student Trainer Spencer Packer. Missing: April Mancuso. UTE TRACK RECORD UTAH’S DOMINANCE OF COLLEGIATE SKIING The University of Utah has built an impressive track record of skiing excellence. With over 60 Ute skiers becoming NCAA champions, Utah has won 11 national championships. In 1983, skiing became co-ed under NCAA jurisdiction. Since that time, Utah has won nine national titles, was the runner-up six times and finished third twice. 2003 ACCOMPLISHMENTS -Kevin Sweeney, in just his fourth year as Utah’s head ski coach, led the co-ed team to the 2003 NCAA Ski Championship Title -It was the 11th national title in Utah’s ski history and its first since 1997 -Utah’s 131-point victory over runner-up Vermont marked the biggest margin of victory at an NCAA Ski Championship -In her first year of NCAA skiing, Katrin Smigun went undefeated and was the only dual winner at -

Lab Experiments Are a Major Source of Knowledge in the Social Sciences
IZA DP No. 4540 Lab Experiments Are a Major Source of Knowledge in the Social Sciences Armin Falk James J. Heckman October 2009 DISCUSSION PAPER SERIES Forschungsinstitut zur Zukunft der Arbeit Institute for the Study of Labor Lab Experiments Are a Major Source of Knowledge in the Social Sciences Armin Falk University of Bonn, CEPR, CESifo and IZA James J. Heckman University of Chicago, University College Dublin, Yale University, American Bar Foundation and IZA Discussion Paper No. 4540 October 2009 IZA P.O. Box 7240 53072 Bonn Germany Phone: +49-228-3894-0 Fax: +49-228-3894-180 E-mail: [email protected] Any opinions expressed here are those of the author(s) and not those of IZA. Research published in this series may include views on policy, but the institute itself takes no institutional policy positions. The Institute for the Study of Labor (IZA) in Bonn is a local and virtual international research center and a place of communication between science, politics and business. IZA is an independent nonprofit organization supported by Deutsche Post Foundation. The center is associated with the University of Bonn and offers a stimulating research environment through its international network, workshops and conferences, data service, project support, research visits and doctoral program. IZA engages in (i) original and internationally competitive research in all fields of labor economics, (ii) development of policy concepts, and (iii) dissemination of research results and concepts to the interested public. IZA Discussion Papers often represent preliminary work and are circulated to encourage discussion. Citation of such a paper should account for its provisional character. -

Lecture 7: the Complex Fourier Transform and the Discrete Fourier Transform (DFT)
Lecture 7: The Complex Fourier Transform and the Discrete Fourier Transform (DFT) c Christopher S. Bretherton Winter 2014 7.1 Fourier analysis and filtering Many data analysis problems involve characterizing data sampled on a regular grid of points, e. g. a time series sampled at some rate, a 2D image made of regularly spaced pixels, or a 3D velocity field from a numerical simulation of fluid turbulence on a regular grid. Often, such problems involve characterizing, detecting, separating or ma- nipulating variability on different scales, e. g. finding a weak systematic signal amidst noise in a time series, edge sharpening in an image, or quantifying the energy of motion across the different sizes of turbulent eddies. Fourier analysis using the Discrete Fourier Transform (DFT) is a fun- damental tool for such problems. It transforms the gridded data into a linear combination of oscillations of different wavelengths. This partitions it into scales which can be separately analyzed and manipulated. The computational utility of Fourier methods rests on the Fast Fourier Transform (FFT) algorithm, developed in the 1960s by Cooley and Tukey, which allows efficient calculation of discrete Fourier coefficients of a periodic function sampled on a regular grid of 2p points (or 2p3q5r with slightly reduced efficiency). 7.2 Example of the FFT Using Matlab, take the FFT of the HW1 wave height time series (length 24 × 60=25325) and plot the result (Fig. 1): load hw1 dat; zhat = fft(z); plot(abs(zhat),’x’) A few elements (the second and last, and to a lesser extent the third and the second from last) have magnitudes that stand above the noise. -

Discretization of Integro-Differential Equations
Discretization of Integro-Differential Equations Modeling Dynamic Fractional Order Viscoelasticity K. Adolfsson1, M. Enelund1,S.Larsson2,andM.Racheva3 1 Dept. of Appl. Mech., Chalmers Univ. of Technology, SE–412 96 G¨oteborg, Sweden 2 Dept. of Mathematics, Chalmers Univ. of Technology, SE–412 96 G¨oteborg, Sweden 3 Dept. of Mathematics, Technical University of Gabrovo, 5300 Gabrovo, Bulgaria Abstract. We study a dynamic model for viscoelastic materials based on a constitutive equation of fractional order. This results in an integro- differential equation with a weakly singular convolution kernel. We dis- cretize in the spatial variable by a standard Galerkin finite element method. We prove stability and regularity estimates which show how the convolution term introduces dissipation into the equation of motion. These are then used to prove a priori error estimates. A numerical ex- periment is included. 1 Introduction Fractional order operators (integrals and derivatives) have proved to be very suit- able for modeling memory effects of various materials and systems of technical interest. In particular, they are very useful when modeling viscoelastic materials, see, e.g., [3]. Numerical methods for quasistatic viscoelasticity problems have been studied, e.g., in [2] and [8]. The drawback of the fractional order viscoelastic models is that the whole strain history must be saved and included in each time step. The most commonly used algorithms for this integration are based on the Lubich convolution quadrature [5] for fractional order operators. In [1, 2], we develop an efficient numerical algorithm based on sparse numerical quadrature earlier studied in [6]. While our earlier work focused on discretization in time for the quasistatic case, we now study space discretization for the fully dynamic equations of mo- tion, which take the form of an integro-differential equation with a weakly singu- lar convolution kernel. -

Combining Epistemic Tools in Systems Biology Sara Green
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Philsci-Archive Final version to be published in Studies of History and Philosophy of Biological and Biomedical Sciences Published online: http://www.sciencedirect.com/science/article/pii/S1369848613000265 When one model is not enough: Combining epistemic tools in systems biology Sara Green Centre for Science Studies, Department of Physics and Astronomy, Ny Munkegade 120, Bld. 1520, Aarhus University, Denmark [email protected] Abstract In recent years, the philosophical focus of the modeling literature has shifted from descriptions of general properties of models to an interest in different model functions. It has been argued that the diversity of models and their correspondingly different epistemic goals are important for developing intelligible scientific theories (Levins, 2006; Leonelli, 2007). However, more knowledge is needed on how a combination of different epistemic means can generate and stabilize new entities in science. This paper will draw on Rheinberger’s practice-oriented account of knowledge production. The conceptual repertoire of Rheinberger’s historical epistemology offers important insights for an analysis of the modelling practice. I illustrate this with a case study on network modeling in systems biology where engineering approaches are applied to the study of biological systems. I shall argue that the use of multiple means of representations is an essential part of the dynamic of knowledge generation. It is because of – rather than in spite of – the diversity of constraints of different models that the interlocking use of different epistemic means creates a potential for knowledge production. -

There Is Only One Fourier Transform Jens V
Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 25 December 2017 doi:10.20944/preprints201712.0173.v1 There is only one Fourier Transform Jens V. Fischer * Microwaves and Radar Institute, German Aerospace Center (DLR), Germany Abstract Four Fourier transforms are usually defined, the Integral Fourier transform, the Discrete-Time Fourier transform (DTFT), the Discrete Fourier transform (DFT) and the Integral Fourier transform for periodic functions. However, starting from their definitions, we show that all four Fourier transforms can be reduced to actually only one Fourier transform, the Fourier transform in the distributional sense. Keywords Integral Fourier Transform, Discrete-Time Fourier Transform (DTFT), Discrete Fourier Transform (DFT), Integral Fourier Transform for periodic functions, Fourier series, Poisson Summation Formula, periodization trick, interpolation trick Introduction Two Important Operations The fact that “there is only one Fourier transform” actually There are two operations which are being strongly related to needs no proof. It is commonly known and often discussed in four different variants of the Fourier transform, i.e., the literature, for example in [1-2]. discretization and periodization. For any real-valued T > 0 and δ(t) being the Dirac impulse, let However frequently asked questions are: (1) What is the difference between calculating the Fourier series and the (1) Fourier transform of a continuous function? (2) What is the difference between Discrete-Time Fourier Transform (DTFT) be the function that results from a discretization of f(t) and let and Discrete Fourier Transform (DFT)? (3) When do we need which Fourier transform? and many others. The default answer (2) today to all these questions is to invite the reader to have a look at the so-called Fourier-Poisson cube, e.g. -

Experimental Philosophy and Feminist Epistemology: Conflicts and Complements
City University of New York (CUNY) CUNY Academic Works All Dissertations, Theses, and Capstone Projects Dissertations, Theses, and Capstone Projects 9-2018 Experimental Philosophy and Feminist Epistemology: Conflicts and Complements Amanda Huminski The Graduate Center, City University of New York How does access to this work benefit ou?y Let us know! More information about this work at: https://academicworks.cuny.edu/gc_etds/2826 Discover additional works at: https://academicworks.cuny.edu This work is made publicly available by the City University of New York (CUNY). Contact: [email protected] EXPERIMENTAL PHILOSOPHY AND FEMINIST EPISTEMOLOGY: CONFLICTS AND COMPLEMENTS by AMANDA HUMINSKI A dissertation submitted to the Graduate Faculty in Philosophy in partial fulfillment of the requirements for the degree of Doctor of Philosophy, The City University of New York 2018 © 2018 AMANDA HUMINSKI All Rights Reserved ii Experimental Philosophy and Feminist Epistemology: Conflicts and Complements By Amanda Huminski This manuscript has been read and accepted for the Graduate Faculty in Philosophy in satisfaction of the dissertation requirement for the degree of Doctor of Philosophy. _______________________________ ________________________________________________ Date Linda Martín Alcoff Chair of Examining Committee _______________________________ ________________________________________________ Date Nickolas Pappas Executive Officer Supervisory Committee: Jesse Prinz Miranda Fricker THE CITY UNIVERSITY OF NEW YORK iii ABSTRACT Experimental Philosophy and Feminist Epistemology: Conflicts and Complements by Amanda Huminski Advisor: Jesse Prinz The recent turn toward experimental philosophy, particularly in ethics and epistemology, might appear to be supported by feminist epistemology, insofar as experimental philosophy signifies a break from the tradition of primarily white, middle-class men attempting to draw universal claims from within the limits of their own experience and research. -

Data Mining Algorithms
Data Management and Exploration © for the original version: Prof. Dr. Thomas Seidl Jiawei Han and Micheline Kamber http://www.cs.sfu.ca/~han/dmbook Data Mining Algorithms Lecture Course with Tutorials Wintersemester 2003/04 Chapter 4: Data Preprocessing Chapter 3: Data Preprocessing Why preprocess the data? Data cleaning Data integration and transformation Data reduction Discretization and concept hierarchy generation Summary WS 2003/04 Data Mining Algorithms 4 – 2 Why Data Preprocessing? Data in the real world is dirty incomplete: lacking attribute values, lacking certain attributes of interest, or containing only aggregate data noisy: containing errors or outliers inconsistent: containing discrepancies in codes or names No quality data, no quality mining results! Quality decisions must be based on quality data Data warehouse needs consistent integration of quality data WS 2003/04 Data Mining Algorithms 4 – 3 Multi-Dimensional Measure of Data Quality A well-accepted multidimensional view: Accuracy (range of tolerance) Completeness (fraction of missing values) Consistency (plausibility, presence of contradictions) Timeliness (data is available in time; data is up-to-date) Believability (user’s trust in the data; reliability) Value added (data brings some benefit) Interpretability (there is some explanation for the data) Accessibility (data is actually available) Broad categories: intrinsic, contextual, representational, and accessibility. WS 2003/04 Data Mining Algorithms 4 – 4 Major Tasks in Data Preprocessing -

Technical Coordin,Ting C9mmi~Tee Rocky Mountain Ski Instructors·A.Sociation
Technical Coordin,ting C9mmi~tee Rocky Mountain Ski Instructors·A.sociation The Basic Principles and Final Forms ot The American Ski Techniqqe The Final Forms at the A.erican Ski Technique are based upon seven Basic Principles. In order to develop a unitorm'demonstration of the Final Forms, there must nece.sarily be a unitorm understanding of the Basic Principle.. All a •• ic Principle. do not apply to all Finished Forms, nor are they equally important in the proPQr execu tion ot the.e ~or... Natural Position is the only principle t~t applies to all Final Forms. Basic PrinCiples - American Ski Technique 1. Natural Position. The primary indication of natural position on skis is that the body be in perfect balance, supported by the bone structure ot the 00411 J:elQ'X' than by muscular effort. All parts of the body must be able to efficiently carry out their skiing ,function.. All joint. should be flexed and in a neutral position, that is to .ay, they should always be capable of either flexing more or ot extending. The hands and arms mU,st be carried in such a manner that they can readily assist balance and be used to plant the poles efficiently. ~hen the skier is in a traverse, orin the process of turning, the necessity to tran.fer weight and edge the .kis .akes angulation a require.ent of natural position. Angulation in turn .ake. it nee•••• r' and natuz.1 to •••u.. • 80derate re verse position with the hips and shoulder. 2. Forward Lean. Forward lean may indicate si.ply a body position in which the center of gravity ot the skier is ahead of the feet.