DOCSLIB.ORG

High Order Regularization of Dirac-Delta Sources in Two Space Dimensions

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
High Order Regularization of Dirac-Delta Sources in Two Space Dimensions INTERNSHIP REPORT High order regularization of Dirac-delta sources in two space dimensions. Author: Supervisors: Wouter DE VRIES Prof. Guustaaf JACOBS s1010239 Jean-Piero SUAREZ HOST INSTITUTION: San Diego State University, San Diego (CA), USA Department of Aerospace Engineering and Engineering Mechanics Computational Fluid Dynamics laboratory Prof. G.B. JACOBS HOME INSTITUTION University of Twente, Enschede, Netherlands Faculty of Engineering Technology Group of Engineering Fluid Dynamics Prof. H.W.M. HOEIJMAKERS March 4, 2015 Abstract In this report the regularization of singular sources appearing in hyperbolic conservation laws is studied. Dirac-delta sources represent small particles which appear as source-terms in for example Particle-laden flow. The Dirac-delta sources are regularized with a high order accurate polynomial based regularization technique. Instead of regularizing a single isolated particle, the aim is to employ the regularization technique for a cloud of particles distributed on a non- uniform grid. By assuming that the resulting force exerted by a cloud of particles can be represented by a continuous function, the influence of the source term can be approximated by the convolution of the continuous function and the regularized Dirac-delta function. It is shown that in one dimension the distribution of the singular sources, represented by the convolution of the contin- uous function and Dirac-delta function, can be approximated with high accuracy using the regularization technique. The method is extended to two dimensions and high order approximations of the source-term are obtained as well. The resulting approximation of the singular sources are interpolated using a polynomial interpolation in order to regain a continuous distribution representing the force exerted by the cloud of particles. Finally the high-order approximation of the singular sources are used to solve the two-dimensional singular advec- tion equation. A Chebyshev spectral collocation method and a third order Total Variation Diminishing Runge-Kutta method are employed to approximate the spatial and temporal derivative. For a single isolated moving source and a stationary cloud of particles high-order accuracy is obtained outside the regularized zones. Inside the regularization zones the results are less satisfying and deserve more attention. The validation of these results and additional experi- ments to study the accuracy of the results, remain as future work. Keywords: Hyperbolic conservation laws, two-dimensional advection equation, regularization, Dirac-delta, singu- lar sources, Chebyshev spectral collocation. 1 Contents 1 Introduction 5 1.1 Background . 5 1.2 Objective . 7 2 Regularization, discretization and interpolation methods 9 2.1 Properties of Dirac-delta and Heaviside function . 9 2.2 Regularization of the Dirac-delta function . 10 2.3 Quadrature methods . 12 2.4 Polynomial Interpolation . 14 2.5 A Chebyshev spectral collocation method . 15 2.6 Time Integration . 17 2.7 Accuracy . 17 3 Regularization of singular sources in 1D 19 3.1 One-dimensional advection equation with singular sources . 19 3.2 Approximation of the singular sources in one dimension . 19 3.3 Conclusion on the one-dimensional results . 24 4 Regularization of singular sources in 2D 25 4.1 Two-dimensional advection equation with singular sources . 25 4.2 Approximation of the singular sources in two dimensions . 27 4.3 Interpolation of the singular sources . 33 4.4 Conclusions on the two-dimensional results . 35 5 Numerical results for the two-dimensional singular advection equation 36 5.1 The two-dimensional advection equation with one single isolated moving particle . 36 5.2 The 2D advection equation with a cloud of moving particles . 38 5.3 Conclusions . 40 6 Conclusions and future work 41 A Convergence order of quadrature rules 43 B Accuracy of the Chebyshev spectral collocation method 46 2 List of Figures 2.1 Two examples of a regularized Dirac-dela function . 11 2.2 The tensor-product of the regularized Dirac-delta functions . 12 3.1 Numerical approximation (top) and pointwise error (bottom) for case 3.1. 21 3.2 Numerical approximation (top) and pointwise error (bottom) for case 3.2. 22 3.3 Numerical approximation (top) and pointwise error (bottom) for case 3.3. 23 3.4 Numerical approximation (top) and pointwise error (bottom) for case 3.4. 24 4.1 Square grid with uniform nodes (left) and square grid with CGL-nodes (right). 26 4.2 Numerical approximation (left) and pointwise error on the square domain (right) for case 4.1. 28 4.3 Numerical approximation (left) and pointwise error on the interior domain (right) for case 4.1. 29 4.4 Numerical approximation (left) and pointwise error on the square domain (right) for case 4.2. 29 4.5 Numerical approximation (left) and pointwise error on the interior domain (right) for case 4.2. 30 4.6 Numerical approximation (left) and pointwise error on the square domain (right) for case 4.3. 30 4.7 Numerical approximation (left) and pointwise error on the interior domain (right) for case 4.3. 31 4.8 Numerical approximation (left) and pointwise error on the square domain (right) for case 4.4. 31 4.9 Numerical approximation (left) and pointwise error on the interior domain (right) for case 4.4. 32 4.10 Cross sections of the numerical approximation for case 4.4 . 33 4.11 One-dimensional polynomial interpolation of the cross sections . 34 4.12 One-dimensional polynomial interpolation of the diagonal . 34 4.13 Numerical approximation (left) and full 2D polynomial interpolation (right) for case 4.4. 35 5.1 Numerical approximation (top-left), regularized analytical solution (top-right), pointwise error (bottom- left), heatmap of the error (bottom-right) for case 5.1. 38 5.2 Numerical solution course grid (top left), numerical solution on fine grid (top right), pointwise error (bottom left), heatmap of the error (bottom right) for case 5.2. 40 B.1 Two-dimensional homogeneous advection equation . 47 B.2 Two-dimensional weigthed L2-norm as function of N .......................... 47 3 List of Tables 3.1 parameters for cases 3.1-3.4 . 20 4.1 Parameters for cases 4.1-4.4 . 27 4.2 L2-norm on the interior domain for cases 4.1-4.4. 28 5.1 parameters for case 5.1 . 37 5.2 L2-norms for case 5.1 . 38 5.3 parameters for case 5.2 . 39 5.4 L2-norms for case 5.2 . 40 A.1 Order of convergence for the one-dimensional Simpson’s rule . 44 A.2 Order of convergence for the two-dimensional Simpson’s rule . 44 A.3 Order of convergence for the two-dimensional Newton-Cotes 7-point rule . 45 4 Chapter 1 Introduction In this report the regularization of singular sources in hyperbolic conservation laws in two spatial dimensions is con- sidered. A high order regularization technique based on compactly-supported piecewise polynomials (presented in [1]) is used to regularize singular Dirac-delta sources. The present study is in continuation of the research discussed in [1], where the regularization of a single isolated particle is discussed. Instead of a single isolated particle, the aim is to regularize a dense, non-uniformly distributed cloud of particles for the simulation of particle-laden flow. The main objective is to improve the accuracy of a high-order and high-resolution particle-source-in-cell method in the simulation of particle-laden flows with shocks [3]. The aim of this chapter is to give an introduction to the problem at hand and discuss the need of a regularization method in order to approximate singular sources in particle-laden flow. Before diving into detail, a brief overview of the background of the research and a motivation for the present research is discussed. 1.1 Background In Engineering problems involving high-speed (compressible) gas flows, such as the flow over a supersonic aircraft and flows encountered in combustion problems, the flow is desribed by the non-linear hyperbolic conservation law: @ Q~ (~x;t) + r · F~ (Q~ ) = S~(Q;~ ~x;t) (1.1) @t Where Q~ are the conserved quantities and F~ is the flux function and S~ respresents the source terms. The hyperbolic nature of these equations allow for discontinuous solutions in the form of shock waves. Since hyperbolic conservation laws govern so many evolution problems in various type of scientific fields, the numerical evaluation of these problems has gained a lot of attention past few decades. The focus has been on the accurate capturing of shock waves. Several methods have been developed in order to capture non-linear shock solutions in numerical approximations accurately [16]. The non-homogenous case with (singular) sources-terms however, have been much less investigated. Particle-laden flow The source terms in equation 1.1 play an important role in engineering problems involving high-speed gas flow inter- acting with liquid or solid particles such as combustion. The flow model describing such a flow is Particle-laden flow. Particle-laden flow is a class of two-phase fluid flow where one of the phases represents the carier gas and the other phase typically represents one or more dilute particles. The carier gas flow is governed by Navier-Stokes equations, which reduce to the Euler equations in case viscosity and heat conduction are neglected (neglecting viscosity and heat-conduction is generally a reasonable assumption in compressible gas dynamics problems). The two-dimensional Euler equations (in Cartesian coordinates) are given by: @ @ @ Q~ (x; y; t) + F~ (Q~ ) + G~ (Q~ ) = S~(Q;~ x; y; t) (1.2) @t @x @y 5 where: Q~ = [ρ, ρu, ρv; ρE] F~ (Q~ ) = [ρu, ρu2 + P; ρuv; (E + P )u] G~ (Q~ ) = [ρv; ρuv; ρv2 + P; (E + P )u] ~ S~ = [0; ρfx; ρfy; ρf · ~u + Qv] And: 1 P = (γ − 1)E − ρu2 (1.3) 2 Clearly equation 1.2 is a hyperbolic conservation law of the same form as equation 1.1.
Load more

Recommended publications
  • Numerical Solution of Ordinary Differential Equations
    NUMERICAL SOLUTION OF ORDINARY DIFFERENTIAL EQUATIONS Kendall Atkinson, Weimin Han, David Stewart University of Iowa Iowa City, Iowa A JOHN WILEY & SONS, INC., PUBLICATION Copyright c 2009 by John Wiley & Sons, Inc. All rights reserved. Published by John Wiley & Sons, Inc., Hoboken, New Jersey. Published simultaneously in Canada. No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under Section 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Center, Inc., 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 646-8600, or on the web at www.copyright.com. Requests to the Publisher for permission should be addressed to the Permissions Department, John Wiley & Sons, Inc., 111 River Street, Hoboken, NJ 07030, (201) 748-6011, fax (201) 748-6008. Limit of Liability/Disclaimer of Warranty: While the publisher and author have used their best efforts in preparing this book, they make no representations or warranties with respect to the accuracy or completeness of the contents of this book and specifically disclaim any implied warranties of merchantability or fitness for a particular purpose. No warranty may be created ore extended by sales representatives or written sales materials. The advice and strategies contained herin may not be suitable for your situation. You should consult with a professional where appropriate. Neither the publisher nor author shall be liable for any loss of profit or any other commercial damages, including but not limited to special, incidental, consequential, or other damages.
    [Show full text]
  • On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle
    On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle Agah D. Garnadi 31 December 2017 Department of Mathematics, Faculty of Mathematics and Natural Sciences, Bogor Agricultural University Jl. Meranti, Kampus IPB Darmaga, Bogor, 16680 Indonesia Abstract This note is addressed to solving biperiodic boundary value prob- lem of biharmonic equation in the unit rectangle. First, we describe the necessary tools, which is discrete Fourier transform for one di- mensional periodic sequence, and then extended the results to 2- dimensional biperiodic sequence. Next, we use the discrete Fourier transform 2-dimensional biperiodic sequence to solve discretization of the biperiodic boundary value problem of Biharmonic Equation. MSC: 15A09; 35K35; 41A15; 41A29; 94A12. Key words: Biharmonic equation, biperiodic boundary value problem, discrete Fourier transform, Partial differential equations, Interpola- tion. 1 Introduction This note is an extension of a work by Henrici [2] on fast solver for Poisson equation to biperiodic boundary value problem of biharmonic equation. This 1 note is organized as follows, in the first part we address the tools needed to solve the problem, i.e. introducing discrete Fourier transform (DFT) follows Henrici's work [2]. The second part, we apply the tools already described in the first part to solve discretization of biperiodic boundary value problem of biharmonic equation in the unit rectangle. The need to solve discretization of biharmonic equation is motivated by its occurence in some applications such as elasticity and fluid flows [1, 4], and recently in image inpainting [3]. Note that the work of Henrici [2] on fast solver for biperiodic Poisson equation can be seen as solving harmonic inpainting.
    [Show full text]
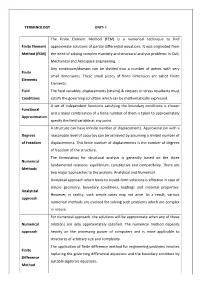
  • TERMINOLOGY UNIT- I Finite Element Method (FEM)
    TERMINOLOGY UNIT- I The Finite Element Method (FEM) is a numerical technique to find Finite Element approximate solutions of partial differential equations. It was originated from Method (FEM) the need of solving complex elasticity and structural analysis problems in Civil, Mechanical and Aerospace engineering. Any continuum/domain can be divided into a number of pieces with very Finite small dimensions. These small pieces of finite dimension are called Finite Elements Elements. Field The field variables, displacements (strains) & stresses or stress resultants must Conditions satisfy the governing condition which can be mathematically expressed. A set of independent functions satisfying the boundary conditions is chosen Functional and a linear combination of a finite number of them is taken to approximately Approximation specify the field variable at any point. A structure can have infinite number of displacements. Approximation with a Degrees reasonable level of accuracy can be achieved by assuming a limited number of of Freedom displacements. This finite number of displacements is the number of degrees of freedom of the structure. The formulation for structural analysis is generally based on the three Numerical fundamental relations: equilibrium, constitutive and compatibility. There are Methods two major approaches to the analysis: Analytical and Numerical. Analytical approach which leads to closed-form solutions is effective in case of simple geometry, boundary conditions, loadings and material properties. Analytical However, in reality, such simple cases may not arise. As a result, various approach numerical methods are evolved for solving such problems which are complex in nature. For numerical approach, the solutions will be approximate when any of these Numerical relations are only approximately satisfied.
    [Show full text]
  • Lecture 7: the Complex Fourier Transform and the Discrete Fourier Transform (DFT)
    Lecture 7: The Complex Fourier Transform and the Discrete Fourier Transform (DFT) c Christopher S. Bretherton Winter 2014 7.1 Fourier analysis and filtering Many data analysis problems involve characterizing data sampled on a regular grid of points, e. g. a time series sampled at some rate, a 2D image made of regularly spaced pixels, or a 3D velocity field from a numerical simulation of fluid turbulence on a regular grid. Often, such problems involve characterizing, detecting, separating or ma- nipulating variability on different scales, e. g. finding a weak systematic signal amidst noise in a time series, edge sharpening in an image, or quantifying the energy of motion across the different sizes of turbulent eddies. Fourier analysis using the Discrete Fourier Transform (DFT) is a fun- damental tool for such problems. It transforms the gridded data into a linear combination of oscillations of different wavelengths. This partitions it into scales which can be separately analyzed and manipulated. The computational utility of Fourier methods rests on the Fast Fourier Transform (FFT) algorithm, developed in the 1960s by Cooley and Tukey, which allows efficient calculation of discrete Fourier coefficients of a periodic function sampled on a regular grid of 2p points (or 2p3q5r with slightly reduced efficiency). 7.2 Example of the FFT Using Matlab, take the FFT of the HW1 wave height time series (length 24 × 60=25325) and plot the result (Fig. 1): load hw1 dat; zhat = fft(z); plot(abs(zhat),’x’) A few elements (the second and last, and to a lesser extent the third and the second from last) have magnitudes that stand above the noise.
    [Show full text]
  • Polarization Fields and Phase Space Densities in Storage Rings: Stroboscopic Averaging and the Ergodic Theorem
    Physica D 234 (2007) 131–149 www.elsevier.com/locate/physd Polarization fields and phase space densities in storage rings: Stroboscopic averaging and the ergodic theorem✩ James A. Ellison∗, Klaus Heinemann Department of Mathematics and Statistics, University of New Mexico, Albuquerque, NM 87131, United States Received 1 May 2007; received in revised form 6 July 2007; accepted 9 July 2007 Available online 14 July 2007 Communicated by C.K.R.T. Jones Abstract A class of orbital motions with volume preserving flows and with vector fields periodic in the “time” parameter θ is defined. Spin motion coupled to the orbital dynamics is then defined, resulting in a class of spin–orbit motions which are important for storage rings. Phase space densities and polarization fields are introduced. It is important, in the context of storage rings, to understand the behavior of periodic polarization fields and phase space densities. Due to the 2π time periodicity of the spin–orbit equations of motion the polarization field, taken at a sequence of increasing time values θ,θ 2π,θ 4π,... , gives a sequence of polarization fields, called the stroboscopic sequence. We show, by using the + + Birkhoff ergodic theorem, that under very general conditions the Cesaro` averages of that sequence converge almost everywhere on phase space to a polarization field which is 2π-periodic in time. This fulfills the main aim of this paper in that it demonstrates that the tracking algorithm for stroboscopic averaging, encoded in the program SPRINT and used in the study of spin motion in storage rings, is mathematically well-founded.
    [Show full text]
  • Discretization of Integro-Differential Equations
    Discretization of Integro-Differential Equations Modeling Dynamic Fractional Order Viscoelasticity K. Adolfsson1, M. Enelund1,S.Larsson2,andM.Racheva3 1 Dept. of Appl. Mech., Chalmers Univ. of Technology, SE–412 96 G¨oteborg, Sweden 2 Dept. of Mathematics, Chalmers Univ. of Technology, SE–412 96 G¨oteborg, Sweden 3 Dept. of Mathematics, Technical University of Gabrovo, 5300 Gabrovo, Bulgaria Abstract. We study a dynamic model for viscoelastic materials based on a constitutive equation of fractional order. This results in an integro- differential equation with a weakly singular convolution kernel. We dis- cretize in the spatial variable by a standard Galerkin finite element method. We prove stability and regularity estimates which show how the convolution term introduces dissipation into the equation of motion. These are then used to prove a priori error estimates. A numerical ex- periment is included. 1 Introduction Fractional order operators (integrals and derivatives) have proved to be very suit- able for modeling memory effects of various materials and systems of technical interest. In particular, they are very useful when modeling viscoelastic materials, see, e.g., [3]. Numerical methods for quasistatic viscoelasticity problems have been studied, e.g., in [2] and [8]. The drawback of the fractional order viscoelastic models is that the whole strain history must be saved and included in each time step. The most commonly used algorithms for this integration are based on the Lubich convolution quadrature [5] for fractional order operators. In [1, 2], we develop an efficient numerical algorithm based on sparse numerical quadrature earlier studied in [6]. While our earlier work focused on discretization in time for the quasistatic case, we now study space discretization for the fully dynamic equations of mo- tion, which take the form of an integro-differential equation with a weakly singu- lar convolution kernel.
    [Show full text]
  • Approximations in Numerical Analysis, Cont'd
    Jim Lambers MAT 460/560 Fall Semester 2009-10 Lecture 7 Notes These notes correspond to Section 1.3 in the text. Approximations in Numerical Analysis, cont'd Convergence Many algorithms in numerical analysis are iterative methods that produce a sequence fαng of ap- proximate solutions which, ideally, converges to a limit α that is the exact solution as n approaches 1. Because we can only perform a finite number of iterations, we cannot obtain the exact solution, and we have introduced computational error. If our iterative method is properly designed, then this computational error will approach zero as n approaches 1. However, it is important that we obtain a sufficiently accurate approximate solution using as few computations as possible. Therefore, it is not practical to simply perform enough iterations so that the computational error is determined to be sufficiently small, because it is possible that another method may yield comparable accuracy with less computational effort. The total computational effort of an iterative method depends on both the effort per iteration and the number of iterations performed. Therefore, in order to determine the amount of compu- tation that is needed to attain a given accuracy, we must be able to measure the error in αn as a function of n. The more rapidly this function approaches zero as n approaches 1, the more rapidly the sequence of approximations fαng converges to the exact solution α, and as a result, fewer iterations are needed to achieve a desired accuracy. We now introduce some terminology that will aid in the discussion of the convergence behavior of iterative methods.
    [Show full text]
  • There Is Only One Fourier Transform Jens V
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 25 December 2017 doi:10.20944/preprints201712.0173.v1 There is only one Fourier Transform Jens V. Fischer * Microwaves and Radar Institute, German Aerospace Center (DLR), Germany Abstract Four Fourier transforms are usually defined, the Integral Fourier transform, the Discrete-Time Fourier transform (DTFT), the Discrete Fourier transform (DFT) and the Integral Fourier transform for periodic functions. However, starting from their definitions, we show that all four Fourier transforms can be reduced to actually only one Fourier transform, the Fourier transform in the distributional sense. Keywords Integral Fourier Transform, Discrete-Time Fourier Transform (DTFT), Discrete Fourier Transform (DFT), Integral Fourier Transform for periodic functions, Fourier series, Poisson Summation Formula, periodization trick, interpolation trick Introduction Two Important Operations The fact that “there is only one Fourier transform” actually There are two operations which are being strongly related to needs no proof. It is commonly known and often discussed in four different variants of the Fourier transform, i.e., the literature, for example in [1-2]. discretization and periodization. For any real-valued T > 0 and δ(t) being the Dirac impulse, let However frequently asked questions are: (1) What is the difference between calculating the Fourier series and the (1) Fourier transform of a continuous function? (2) What is the difference between Discrete-Time Fourier Transform (DTFT) be the function that results from a discretization of f(t) and let and Discrete Fourier Transform (DFT)? (3) When do we need which Fourier transform? and many others. The default answer (2) today to all these questions is to invite the reader to have a look at the so-called Fourier-Poisson cube, e.g.
    [Show full text]
  • Data Mining Algorithms
    Data Management and Exploration © for the original version: Prof. Dr. Thomas Seidl Jiawei Han and Micheline Kamber http://www.cs.sfu.ca/~han/dmbook Data Mining Algorithms Lecture Course with Tutorials Wintersemester 2003/04 Chapter 4: Data Preprocessing Chapter 3: Data Preprocessing Why preprocess the data? Data cleaning Data integration and transformation Data reduction Discretization and concept hierarchy generation Summary WS 2003/04 Data Mining Algorithms 4 – 2 Why Data Preprocessing? Data in the real world is dirty incomplete: lacking attribute values, lacking certain attributes of interest, or containing only aggregate data noisy: containing errors or outliers inconsistent: containing discrepancies in codes or names No quality data, no quality mining results! Quality decisions must be based on quality data Data warehouse needs consistent integration of quality data WS 2003/04 Data Mining Algorithms 4 – 3 Multi-Dimensional Measure of Data Quality A well-accepted multidimensional view: Accuracy (range of tolerance) Completeness (fraction of missing values) Consistency (plausibility, presence of contradictions) Timeliness (data is available in time; data is up-to-date) Believability (user’s trust in the data; reliability) Value added (data brings some benefit) Interpretability (there is some explanation for the data) Accessibility (data is actually available) Broad categories: intrinsic, contextual, representational, and accessibility. WS 2003/04 Data Mining Algorithms 4 – 4 Major Tasks in Data Preprocessing
    [Show full text]
  • On the Three Methods for Bounding the Rate of Convergence for Some Continuous-Time Markov Chains
    On the Three Methods for Bounding the Rate of Convergence for some Continuous-time Markov Chains Alexander Zeifman∗ Yacov Satiny Anastasia Kryukovaz Rostislav Razumchik§ Ksenia Kiseleva{ Galina Shilovak Abstract. Consideration is given to the three different analytical methods for the computation of upper bounds for the rate of convergence to the limiting regime of one specific class of (in)homogeneous continuous- time Markov chains. This class is particularly suited to describe evolutions of the total number of customers in (in)homogeneous M=M=S queueing systems with possibly state-dependent arrival and service intensities, batch arrivals and services. One of the methods is based on the logarithmic norm of a linear operator function; the other two rely on Lyapunov functions and differential inequalities, respectively. Less restrictive conditions (compared to those known from the literature) under which the methods are applicable, are being formulated. Two numerical examples are given. It is also shown that for homogeneous birth-death Markov processes defined on a finite state space with all transition rates being positive, all methods yield the same sharp upper bound. ∗Vologda State University, Vologda, Russia; Institute of Informatics Problems, Federal Research Center “Computer Science and Control”, Russian Academy of Sciences, Moscow, arXiv:1911.04086v2 [math.PR] 24 Feb 2020 Russia; Vologda Research Center of the Russian Academy of Sciences, Vologda, Russia. E-mail: [email protected] yVologda State University, Vologda, Russia zVologda State
    [Show full text]
  • CONVERGENCE RATES of MARKOV CHAINS 1. Orientation 1
    CONVERGENCE RATES OF MARKOV CHAINS STEVEN P. LALLEY CONTENTS 1. Orientation 1 1.1. Example 1: Random-to-Top Card Shuffling 1 1.2. Example 2: The Ehrenfest Urn Model of Diffusion 2 1.3. Example 3: Metropolis-Hastings Algorithm 4 1.4. Reversible Markov Chains 5 1.5. Exercises: Reversiblity, Symmetries and Stationary Distributions 8 2. Coupling 9 2.1. Coupling and Total Variation Distance 9 2.2. Coupling Constructions and Convergence of Markov Chains 10 2.3. Couplings for the Ehrenfest Urn and Random-to-Top Shuffling 12 2.4. The Coupon Collector’s Problem 13 2.5. Exercises 15 2.6. Convergence Rates for the Ehrenfest Urn and Random-to-Top 16 2.7. Exercises 17 3. Spectral Analysis 18 3.1. Transition Kernel of a Reversible Markov Chain 18 3.2. Spectrum of the Ehrenfest random walk 21 3.3. Rate of convergence of the Ehrenfest random walk 23 1. ORIENTATION Finite-state Markov chains have stationary distributions, and irreducible, aperiodic, finite- state Markov chains have unique stationary distributions. Furthermore, for any such chain the n−step transition probabilities converge to the stationary distribution. In various ap- plications – especially in Markov chain Monte Carlo, where one runs a Markov chain on a computer to simulate a random draw from the stationary distribution – it is desirable to know how many steps it takes for the n−step transition probabilities to become close to the stationary probabilities. These notes will introduce several of the most basic and important techniques for studying this problem, coupling and spectral analysis. We will focus on two Markov chains for which the convergence rate is of particular interest: (1) the random-to-top shuffling model and (2) the Ehrenfest urn model.
    [Show full text]
  • Verification and Validation in Computational Fluid Dynamics1
    SAND2002 - 0529 Unlimited Release Printed March 2002 Verification and Validation in Computational Fluid Dynamics1 William L. Oberkampf Validation and Uncertainty Estimation Department Timothy G. Trucano Optimization and Uncertainty Estimation Department Sandia National Laboratories P. O. Box 5800 Albuquerque, New Mexico 87185 Abstract Verification and validation (V&V) are the primary means to assess accuracy and reliability in computational simulations. This paper presents an extensive review of the literature in V&V in computational fluid dynamics (CFD), discusses methods and procedures for assessing V&V, and develops a number of extensions to existing ideas. The review of the development of V&V terminology and methodology points out the contributions from members of the operations research, statistics, and CFD communities. Fundamental issues in V&V are addressed, such as code verification versus solution verification, model validation versus solution validation, the distinction between error and uncertainty, conceptual sources of error and uncertainty, and the relationship between validation and prediction. The fundamental strategy of verification is the identification and quantification of errors in the computational model and its solution. In verification activities, the accuracy of a computational solution is primarily measured relative to two types of highly accurate solutions: analytical solutions and highly accurate numerical solutions. Methods for determining the accuracy of numerical solutions are presented and the importance of software testing during verification activities is emphasized. The fundamental strategy of 1Accepted for publication in the review journal Progress in Aerospace Sciences. 3 validation is to assess how accurately the computational results compare with the experimental data, with quantified error and uncertainty estimates for both.
    [Show full text]