DOCSLIB.ORG

Data Mining Algorithms

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Data Mining Algorithms Data Management and Exploration © for the original version: Prof. Dr. Thomas Seidl Jiawei Han and Micheline Kamber http://www.cs.sfu.ca/~han/dmbook Data Mining Algorithms Lecture Course with Tutorials Wintersemester 2003/04 Chapter 4: Data Preprocessing Chapter 3: Data Preprocessing Why preprocess the data? Data cleaning Data integration and transformation Data reduction Discretization and concept hierarchy generation Summary WS 2003/04 Data Mining Algorithms 4 – 2 Why Data Preprocessing? Data in the real world is dirty incomplete: lacking attribute values, lacking certain attributes of interest, or containing only aggregate data noisy: containing errors or outliers inconsistent: containing discrepancies in codes or names No quality data, no quality mining results! Quality decisions must be based on quality data Data warehouse needs consistent integration of quality data WS 2003/04 Data Mining Algorithms 4 – 3 Multi-Dimensional Measure of Data Quality A well-accepted multidimensional view: Accuracy (range of tolerance) Completeness (fraction of missing values) Consistency (plausibility, presence of contradictions) Timeliness (data is available in time; data is up-to-date) Believability (user’s trust in the data; reliability) Value added (data brings some benefit) Interpretability (there is some explanation for the data) Accessibility (data is actually available) Broad categories: intrinsic, contextual, representational, and accessibility. WS 2003/04 Data Mining Algorithms 4 – 4 Major Tasks in Data Preprocessing Data cleaning Fill in missing values, smooth noisy data, identify or remove outliers, and resolve inconsistencies Data integration Integration of multiple databases, data cubes, or files Data transformation Normalization and aggregation Data reduction Obtains reduced representation in volume but produces the same or similar analytical results Data discretization Part of data reduction but with particular importance, especially for numerical data WS 2003/04 Data Mining Algorithms 4 – 5 Chapter 3: Data Preprocessing Why preprocess the data? Data cleaning Data integration and transformation Data reduction Discretization and concept hierarchy generation Summary WS 2003/04 Data Mining Algorithms 4 – 6 Data Cleaning Data cleaning tasks Fill in missing values Identify outliers and smooth out noisy data Correct inconsistent data WS 2003/04 Data Mining Algorithms 4 – 7 Missing Data Data is not always available E.g., many tuples have no recorded value for several attributes, such as customer income in sales data Missing data may be due to equipment malfunction inconsistent with other recorded data and thus deleted data not entered due to misunderstanding certain data may not be considered important at the time of entry not register history or changes of the data Missing data may need to be inferred. WS 2003/04 Data Mining Algorithms 4 – 8 How to Handle Missing Data? Ignore the tuple: usually done when class label is missing (not effective when the percentage of missing values per attribute varies considerably. Fill in the missing value manually: tedious (i.e., boring & time- consuming), infeasible? Use a global constant to fill in the missing value: e.g., a default value, or “unknown”, a new class?! – not recommended! Use the attribute mean (average value) to fill in the missing value Use the attribute mean for all samples belonging to the same class to fill in the missing value: smarter Use the most probable value to fill in the missing value: inference- based such as Bayesian formula or decision tree WS 2003/04 Data Mining Algorithms 4 – 9 Noisy Data Noise: random error or variance in a measured variable Incorrect attribute values may due to faulty data collection instruments data entry problems data transmission problems technology limitation inconsistency in naming convention Other data problems which requires data cleaning duplicate records incomplete data inconsistent data WS 2003/04 Data Mining Algorithms 4 – 10 How to Handle Noisy Data? Binning method: first sort data and partition into (equi-depth) bins then one can smooth by bin means, smooth by bin median, smooth by bin boundaries, etc. Clustering detect and remove outliers Combined computer and human inspection detect suspicious values and check by human Regression smooth by fitting the data into regression functions WS 2003/04 Data Mining Algorithms 4 – 11 Noisy Data—Simple Discretization (1) Equal-width (distance) partitioning: It divides the range into N intervals of equal size: uniform grid if A and B are the lowest and highest values of the attribute, the width of intervals will be: W = (B-A)/N. The most straightforward Shortcoming: outliers may dominate presentation 12 12 10 Skewed data is not handled well. 8 8 6 6 Example (data sorted, here: 10 bins): 5 5, 7, 8, 8, 9, 11, 13, 13, 14, 14, 4 14, 15, 17, 17, 17, 18, 19, 23, 24, 2 1 25, 26, 26, 26, 27, 28, 32, 34, 36, 0 0 0 0 0 0 37, 38, 39, 97 1-10 21-30 31-40 41-50 51-60 61-70 71-80 81-90 11-20 91-100 WS 2003/04 Data Mining Algorithms 4 – 12 Noisy Data—Simple Discretization (2) Equal-depth (frequency) partitioning: It divides the range into N intervals, each containing approximately same number of samples (quantile-based approach) 8 8 8 8 8 Good data scaling 7 Managing categorical attributes 6 can be tricky. 5 4 3 2 Same Example (here: 4 bins): 1 5, 7, 8, 8, 9, 11, 13, 13, 14, 14, 0 14, 15, 17, 17, 17, 18, 19, 23, 24, 1-13 14-17 18-26 25, 26, 26, 26, 27, 28, 32, 34, 34, 27-100 36, 37, 37, 38, 39, 97 1- 14 - 18 - 27 - 13 17 26 100 WS 2003/04 Data Mining Algorithms 4 – 13 Noisy Data— Binning Methods for Data Smoothing * Sorted data for price (in dollars): 35 4, 8, 9, 15, 21, 21, 24, 30 price [US$] 25 25, 26, 28, 29, 34 20 15 * Partition into (equi-depth) bins: 10 - Bin 1: 4, 8, 9, 15 5 0 - Bin 2: 21, 21, 24, 25 35 - Bin 3: 26, 28, 29, 34 30 bin means 25 * Smoothing by bin means: 20 15 - Bin 1: 9, 9, 9, 9 10 - Bin 2: 23, 23, 23, 23 5 0 - Bin 3: 29, 29, 29, 29 35 * Smoothing by bin boundaries: 30 bin boundaries 25 - Bin 1: 4, 4, 4, 15 20 15 - Bin 2: 21, 21, 25, 25 10 5 - Bin 3: 26, 26, 26, 34 0 WS 2003/04 Data Mining Algorithms 4 – 14 Noisy Data—Cluster Analysis Detect and remove outliers WS 2003/04 Data Mining Algorithms 4 – 15 Noisy Data—Regression y Smooth data according to some regression function Y1 Y1’ y = x + 1 X1 x WS 2003/04 Data Mining Algorithms 4 – 16 Chapter 3: Data Preprocessing Why preprocess the data? Data cleaning Data integration and transformation Data reduction Discretization and concept hierarchy generation Summary WS 2003/04 Data Mining Algorithms 4 – 17 Data Integration Data integration: combines data from multiple sources into a coherent store Schema integration integrate metadata from different sources Entity identification problem: identify real world entities from multiple data sources, e.g., A.cust-id ≡ B.cust-# Detecting and resolving data value conflicts for the same real world entity, attribute values from different sources are different possible reasons: different representations, different scales, e.g., metric vs. British units WS 2003/04 Data Mining Algorithms 4 – 18 Handling Redundant Data in Data Integration Redundant data occur often when integrating multiple databases The same attribute may have different names in different databases One attribute may be a “derived” attribute in another table, e.g., birthday vs. age; annual revenue Redundant data may be able to be detected by correlational analysis Careful integration of the data from multiple sources may help reduce/avoid redundancies and inconsistencies and improve mining speed and quality WS 2003/04 Data Mining Algorithms 4 – 19 Data Transformation Smoothing: remove noise from data Aggregation: summarization, data cube construction Generalization: concept hierarchy climbing e.g., {young, middle-aged, senior} rather than {1…100} Normalization: scaled to fall within a small, specified range min-max normalization z-score normalization (= zero-mean normalization) normalization by decimal scaling Attribute/feature construction New attributes constructed from the given ones e.g., age = years(current_date – birthday) WS 2003/04 Data Mining Algorithms 4 – 20 Data Transformation: min-max Normalization min-max normalization new_max − new_min v'= ()v − min A A + new_min A − A maxA minA transforms data linearly to a new range range outliers may be detected afterwards as well new_maxA slope is: new_max − new_min new_min A A A − maxA minA minA maxA WS 2003/04 Data Mining Algorithms 4 – 21 Data Transformation: zero-mean Normalization zero-mean (z-score) normalization v − mean v'= A std _ devA Particularly useful if min/max values are unknown Outliers dominate min/max normalization WS 2003/04 Data Mining Algorithms 4 – 22 Data Transformation: Normalization by Decimal Scaling normalization by decimal scaling v v'= Where j is the smallest integer such that max(|ν’|) < 1 10 j New data range: 0=|ν’| < 1 i.e., –1 < ν’ < 1 Normalization (in general) is important when considering several attributes in combination. Large value ranges should not dominate small ones of other attributes WS 2003/04 Data Mining Algorithms 4 – 23 Chapter 3: Data Preprocessing Why preprocess the data? Data cleaning Data integration and transformation Data reduction Discretization and concept hierarchy generation Summary WS 2003/04 Data Mining Algorithms 4 – 24 Data Reduction Strategies Warehouse may store terabytes of data: Complex data analysis/mining may take a very long time to run on the complete data set Data reduction Obtains a reduced representation of the data set that is much smaller in volume but yet produces the same (or almost the same) analytical results Data reduction strategies Data cube aggregation Dimensionality reduction Numerosity reduction Discretization and concept hierarchy generation WS 2003/04 Data Mining Algorithms 4 – 25 Data Cube Aggregation The lowest level of a data cube the aggregated data for an individual entity of interest e.g., a customer in a phone calling data warehouse.
Load more

Recommended publications
  • Moving Average Filters
    CHAPTER 15 Moving Average Filters The moving average is the most common filter in DSP, mainly because it is the easiest digital filter to understand and use. In spite of its simplicity, the moving average filter is optimal for a common task: reducing random noise while retaining a sharp step response. This makes it the premier filter for time domain encoded signals. However, the moving average is the worst filter for frequency domain encoded signals, with little ability to separate one band of frequencies from another. Relatives of the moving average filter include the Gaussian, Blackman, and multiple- pass moving average. These have slightly better performance in the frequency domain, at the expense of increased computation time. Implementation by Convolution As the name implies, the moving average filter operates by averaging a number of points from the input signal to produce each point in the output signal. In equation form, this is written: EQUATION 15-1 Equation of the moving average filter. In M &1 this equation, x[ ] is the input signal, y[ ] is ' 1 % y[i] j x [i j ] the output signal, and M is the number of M j'0 points used in the moving average. This equation only uses points on one side of the output sample being calculated. Where x[ ] is the input signal, y[ ] is the output signal, and M is the number of points in the average. For example, in a 5 point moving average filter, point 80 in the output signal is given by: x [80] % x [81] % x [82] % x [83] % x [84] y [80] ' 5 277 278 The Scientist and Engineer's Guide to Digital Signal Processing As an alternative, the group of points from the input signal can be chosen symmetrically around the output point: x[78] % x[79] % x[80] % x[81] % x[82] y[80] ' 5 This corresponds to changing the summation in Eq.
    [Show full text]
  • On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle
    On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle Agah D. Garnadi 31 December 2017 Department of Mathematics, Faculty of Mathematics and Natural Sciences, Bogor Agricultural University Jl. Meranti, Kampus IPB Darmaga, Bogor, 16680 Indonesia Abstract This note is addressed to solving biperiodic boundary value prob- lem of biharmonic equation in the unit rectangle. First, we describe the necessary tools, which is discrete Fourier transform for one di- mensional periodic sequence, and then extended the results to 2- dimensional biperiodic sequence. Next, we use the discrete Fourier transform 2-dimensional biperiodic sequence to solve discretization of the biperiodic boundary value problem of Biharmonic Equation. MSC: 15A09; 35K35; 41A15; 41A29; 94A12. Key words: Biharmonic equation, biperiodic boundary value problem, discrete Fourier transform, Partial differential equations, Interpola- tion. 1 Introduction This note is an extension of a work by Henrici [2] on fast solver for Poisson equation to biperiodic boundary value problem of biharmonic equation. This 1 note is organized as follows, in the first part we address the tools needed to solve the problem, i.e. introducing discrete Fourier transform (DFT) follows Henrici's work [2]. The second part, we apply the tools already described in the first part to solve discretization of biperiodic boundary value problem of biharmonic equation in the unit rectangle. The need to solve discretization of biharmonic equation is motivated by its occurence in some applications such as elasticity and fluid flows [1, 4], and recently in image inpainting [3]. Note that the work of Henrici [2] on fast solver for biperiodic Poisson equation can be seen as solving harmonic inpainting.
    [Show full text]
  • Spatial Domain Low-Pass Filters
    Low Pass Filtering Why use Low Pass filtering? • Remove random noise • Remove periodic noise • Reveal a background pattern 1 Effects on images • Remove banding effects on images • Smooth out Img-Img mis-registration • Blurring of image Types of Low Pass Filters • Moving average filter • Median filter • Adaptive filter 2 Moving Ave Filter Example • A single (very short) scan line of an image • {1,8,3,7,8} • Moving Ave using interval of 3 (must be odd) • First number (1+8+3)/3 =4 • Second number (8+3+7)/3=6 • Third number (3+7+8)/3=6 • First and last value set to 0 Two Dimensional Moving Ave 3 Moving Average of Scan Line 2D Moving Average Filter • Spatial domain filter • Places average in center • Edges are set to 0 usually to maintain size 4 Spatial Domain Filter Moving Average Filter Effects • Reduces overall variability of image • Lowers contrast • Noise components reduced • Blurs the overall appearance of image 5 Moving Average images Median Filter The median utilizes the median instead of the mean. The median is the middle positional value. 6 Median Example • Another very short scan line • Data set {2,8,4,6,27} interval of 5 • Ranked {2,4,6,8,27} • Median is 6, central value 4 -> 6 Median Filter • Usually better for filtering • - Less sensitive to errors or extremes • - Median is always a value of the set • - Preserves edges • - But requires more computation 7 Moving Ave vs. Median Filtering Adaptive Filters • Based on mean and variance • Good at Speckle suppression • Sigma filter best known • - Computes mean and std dev for window • - Values outside of +-2 std dev excluded • - If too few values, (<k) uses value to left • - Later versions use weighting 8 Adaptive Filters • Improvements to Sigma filtering - Chi-square testing - Weighting - Local order histogram statistics - Edge preserving smoothing Adaptive Filters 9 Final PowerPoint Numerical Slide Value (The End) 10.
    [Show full text]
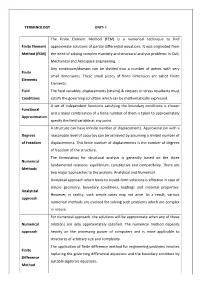
  • TERMINOLOGY UNIT- I Finite Element Method (FEM)
    TERMINOLOGY UNIT- I The Finite Element Method (FEM) is a numerical technique to find Finite Element approximate solutions of partial differential equations. It was originated from Method (FEM) the need of solving complex elasticity and structural analysis problems in Civil, Mechanical and Aerospace engineering. Any continuum/domain can be divided into a number of pieces with very Finite small dimensions. These small pieces of finite dimension are called Finite Elements Elements. Field The field variables, displacements (strains) & stresses or stress resultants must Conditions satisfy the governing condition which can be mathematically expressed. A set of independent functions satisfying the boundary conditions is chosen Functional and a linear combination of a finite number of them is taken to approximately Approximation specify the field variable at any point. A structure can have infinite number of displacements. Approximation with a Degrees reasonable level of accuracy can be achieved by assuming a limited number of of Freedom displacements. This finite number of displacements is the number of degrees of freedom of the structure. The formulation for structural analysis is generally based on the three Numerical fundamental relations: equilibrium, constitutive and compatibility. There are Methods two major approaches to the analysis: Analytical and Numerical. Analytical approach which leads to closed-form solutions is effective in case of simple geometry, boundary conditions, loadings and material properties. Analytical However, in reality, such simple cases may not arise. As a result, various approach numerical methods are evolved for solving such problems which are complex in nature. For numerical approach, the solutions will be approximate when any of these Numerical relations are only approximately satisfied.
    [Show full text]
  • Lecture 7: the Complex Fourier Transform and the Discrete Fourier Transform (DFT)
    Lecture 7: The Complex Fourier Transform and the Discrete Fourier Transform (DFT) c Christopher S. Bretherton Winter 2014 7.1 Fourier analysis and filtering Many data analysis problems involve characterizing data sampled on a regular grid of points, e. g. a time series sampled at some rate, a 2D image made of regularly spaced pixels, or a 3D velocity field from a numerical simulation of fluid turbulence on a regular grid. Often, such problems involve characterizing, detecting, separating or ma- nipulating variability on different scales, e. g. finding a weak systematic signal amidst noise in a time series, edge sharpening in an image, or quantifying the energy of motion across the different sizes of turbulent eddies. Fourier analysis using the Discrete Fourier Transform (DFT) is a fun- damental tool for such problems. It transforms the gridded data into a linear combination of oscillations of different wavelengths. This partitions it into scales which can be separately analyzed and manipulated. The computational utility of Fourier methods rests on the Fast Fourier Transform (FFT) algorithm, developed in the 1960s by Cooley and Tukey, which allows efficient calculation of discrete Fourier coefficients of a periodic function sampled on a regular grid of 2p points (or 2p3q5r with slightly reduced efficiency). 7.2 Example of the FFT Using Matlab, take the FFT of the HW1 wave height time series (length 24 × 60=25325) and plot the result (Fig. 1): load hw1 dat; zhat = fft(z); plot(abs(zhat),’x’) A few elements (the second and last, and to a lesser extent the third and the second from last) have magnitudes that stand above the noise.
    [Show full text]
  • Discretization of Integro-Differential Equations
    Discretization of Integro-Differential Equations Modeling Dynamic Fractional Order Viscoelasticity K. Adolfsson1, M. Enelund1,S.Larsson2,andM.Racheva3 1 Dept. of Appl. Mech., Chalmers Univ. of Technology, SE–412 96 G¨oteborg, Sweden 2 Dept. of Mathematics, Chalmers Univ. of Technology, SE–412 96 G¨oteborg, Sweden 3 Dept. of Mathematics, Technical University of Gabrovo, 5300 Gabrovo, Bulgaria Abstract. We study a dynamic model for viscoelastic materials based on a constitutive equation of fractional order. This results in an integro- differential equation with a weakly singular convolution kernel. We dis- cretize in the spatial variable by a standard Galerkin finite element method. We prove stability and regularity estimates which show how the convolution term introduces dissipation into the equation of motion. These are then used to prove a priori error estimates. A numerical ex- periment is included. 1 Introduction Fractional order operators (integrals and derivatives) have proved to be very suit- able for modeling memory effects of various materials and systems of technical interest. In particular, they are very useful when modeling viscoelastic materials, see, e.g., [3]. Numerical methods for quasistatic viscoelasticity problems have been studied, e.g., in [2] and [8]. The drawback of the fractional order viscoelastic models is that the whole strain history must be saved and included in each time step. The most commonly used algorithms for this integration are based on the Lubich convolution quadrature [5] for fractional order operators. In [1, 2], we develop an efficient numerical algorithm based on sparse numerical quadrature earlier studied in [6]. While our earlier work focused on discretization in time for the quasistatic case, we now study space discretization for the fully dynamic equations of mo- tion, which take the form of an integro-differential equation with a weakly singu- lar convolution kernel.
    [Show full text]
  • Review of Smoothing Methods for Enhancement of Noisy Data from Heavy-Duty LHD Mining Machines
    E3S Web of Conferences 29, 00011 (2018) https://doi.org/10.1051/e3sconf/20182900011 XVIIth Conference of PhD Students and Young Scientists Review of smoothing methods for enhancement of noisy data from heavy-duty LHD mining machines Jacek Wodecki1, Anna Michalak2, and Paweł Stefaniak2 1Machinery Systems Division, Wroclaw University of Science and Technology, Wroclaw, Poland 2KGHM Cuprum R&D Ltd., Wroclaw, Poland Abstract. Appropriate analysis of data measured on heavy-duty mining machines is essential for processes monitoring, management and optimization. Some particular classes of machines, for example LHD (load-haul-dump) machines, hauling trucks, drilling/bolting machines etc. are characterized with cyclicity of operations. In those cases, identification of cycles and their segments or in other words – simply data segmen- tation is a key to evaluate their performance, which may be very useful from the man- agement point of view, for example leading to introducing optimization to the process. However, in many cases such raw signals are contaminated with various artifacts, and in general are expected to be very noisy, which makes the segmentation task very difficult or even impossible. To deal with that problem, there is a need for efficient smoothing meth- ods that will allow to retain informative trends in the signals while disregarding noises and other undesired non-deterministic components. In this paper authors present a review of various approaches to diagnostic data smoothing. Described methods can be used in a fast and efficient way, effectively cleaning the signals while preserving informative de- terministic behaviour, that is a crucial to precise segmentation and other approaches to industrial data analysis.
    [Show full text]
  • There Is Only One Fourier Transform Jens V
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 25 December 2017 doi:10.20944/preprints201712.0173.v1 There is only one Fourier Transform Jens V. Fischer * Microwaves and Radar Institute, German Aerospace Center (DLR), Germany Abstract Four Fourier transforms are usually defined, the Integral Fourier transform, the Discrete-Time Fourier transform (DTFT), the Discrete Fourier transform (DFT) and the Integral Fourier transform for periodic functions. However, starting from their definitions, we show that all four Fourier transforms can be reduced to actually only one Fourier transform, the Fourier transform in the distributional sense. Keywords Integral Fourier Transform, Discrete-Time Fourier Transform (DTFT), Discrete Fourier Transform (DFT), Integral Fourier Transform for periodic functions, Fourier series, Poisson Summation Formula, periodization trick, interpolation trick Introduction Two Important Operations The fact that “there is only one Fourier transform” actually There are two operations which are being strongly related to needs no proof. It is commonly known and often discussed in four different variants of the Fourier transform, i.e., the literature, for example in [1-2]. discretization and periodization. For any real-valued T > 0 and δ(t) being the Dirac impulse, let However frequently asked questions are: (1) What is the difference between calculating the Fourier series and the (1) Fourier transform of a continuous function? (2) What is the difference between Discrete-Time Fourier Transform (DTFT) be the function that results from a discretization of f(t) and let and Discrete Fourier Transform (DFT)? (3) When do we need which Fourier transform? and many others. The default answer (2) today to all these questions is to invite the reader to have a look at the so-called Fourier-Poisson cube, e.g.
    [Show full text]
  • Verification and Validation in Computational Fluid Dynamics1
    SAND2002 - 0529 Unlimited Release Printed March 2002 Verification and Validation in Computational Fluid Dynamics1 William L. Oberkampf Validation and Uncertainty Estimation Department Timothy G. Trucano Optimization and Uncertainty Estimation Department Sandia National Laboratories P. O. Box 5800 Albuquerque, New Mexico 87185 Abstract Verification and validation (V&V) are the primary means to assess accuracy and reliability in computational simulations. This paper presents an extensive review of the literature in V&V in computational fluid dynamics (CFD), discusses methods and procedures for assessing V&V, and develops a number of extensions to existing ideas. The review of the development of V&V terminology and methodology points out the contributions from members of the operations research, statistics, and CFD communities. Fundamental issues in V&V are addressed, such as code verification versus solution verification, model validation versus solution validation, the distinction between error and uncertainty, conceptual sources of error and uncertainty, and the relationship between validation and prediction. The fundamental strategy of verification is the identification and quantification of errors in the computational model and its solution. In verification activities, the accuracy of a computational solution is primarily measured relative to two types of highly accurate solutions: analytical solutions and highly accurate numerical solutions. Methods for determining the accuracy of numerical solutions are presented and the importance of software testing during verification activities is emphasized. The fundamental strategy of 1Accepted for publication in the review journal Progress in Aerospace Sciences. 3 validation is to assess how accurately the computational results compare with the experimental data, with quantified error and uncertainty estimates for both.
    [Show full text]
  • Image Smoothening and Sharpening Using Frequency Domain Filtering Technique
    International Journal of Emerging Technologies in Engineering Research (IJETER) Volume 5, Issue 4, April (2017) www.ijeter.everscience.org Image Smoothening and Sharpening using Frequency Domain Filtering Technique Swati Dewangan M.Tech. Scholar, Computer Networks, Bhilai Institute of Technology, Durg, India. Anup Kumar Sharma M.Tech. Scholar, Computer Networks, Bhilai Institute of Technology, Durg, India. Abstract – Images are used in various fields to help monitoring The content of this paper is organized as follows: Section I processes such as images in fingerprint evaluation, satellite gives introduction to the topic and projects fundamental monitoring, medical diagnostics, underwater areas, etc. Image background. Section II describes the types of image processing techniques is adopted as an optimized method to help enhancement techniques. Section III defines the operations the processing tasks efficiently. The development of image applied for image filtering. Section IV shows results and processing software helps the image editing process effectively. Image enhancement algorithms offer a wide variety of approaches discussions. Section V concludes the proposed approach and for modifying original captured images to achieve visually its outcome. acceptable images. In this paper, we apply frequency domain 1.1 Digital Image Processing filters to generate an enhanced image. Simulation outputs results in noise reduction, contrast enhancement, smoothening and Digital image processing is a part of signal processing which sharpening of the enhanced image. uses computer algorithms to perform image processing on Index Terms – Digital Image Processing, Fourier Transforms, digital images. It has numerous applications in different studies High-pass Filters, Low-pass Filters, Image Enhancement. and researches of science and technology. The fundamental steps in Digital Image processing are image acquisition, image 1.
    [Show full text]
  • High Order Regularization of Dirac-Delta Sources in Two Space Dimensions
    INTERNSHIP REPORT High order regularization of Dirac-delta sources in two space dimensions. Author: Supervisors: Wouter DE VRIES Prof. Guustaaf JACOBS s1010239 Jean-Piero SUAREZ HOST INSTITUTION: San Diego State University, San Diego (CA), USA Department of Aerospace Engineering and Engineering Mechanics Computational Fluid Dynamics laboratory Prof. G.B. JACOBS HOME INSTITUTION University of Twente, Enschede, Netherlands Faculty of Engineering Technology Group of Engineering Fluid Dynamics Prof. H.W.M. HOEIJMAKERS March 4, 2015 Abstract In this report the regularization of singular sources appearing in hyperbolic conservation laws is studied. Dirac-delta sources represent small particles which appear as source-terms in for example Particle-laden flow. The Dirac-delta sources are regularized with a high order accurate polynomial based regularization technique. Instead of regularizing a single isolated particle, the aim is to employ the regularization technique for a cloud of particles distributed on a non- uniform grid. By assuming that the resulting force exerted by a cloud of particles can be represented by a continuous function, the influence of the source term can be approximated by the convolution of the continuous function and the regularized Dirac-delta function. It is shown that in one dimension the distribution of the singular sources, represented by the convolution of the contin- uous function and Dirac-delta function, can be approximated with high accuracy using the regularization technique. The method is extended to two dimensions and high order approximations of the source-term are obtained as well. The resulting approximation of the singular sources are interpolated using a polynomial interpolation in order to regain a continuous distribution representing the force exerted by the cloud of particles.
    [Show full text]
  • On Convergence of the Immersed Boundary Method for Elliptic Interface Problems
    On convergence of the immersed boundary method for elliptic interface problems Zhilin Li∗ January 26, 2012 Abstract Peskin's Immersed Boundary (IB) method is one of the most popular numerical methods for many years and has been applied to problems in mathematical biology, fluid mechanics, material sciences, and many other areas. Peskin's IB method is associated with discrete delta functions. It is believed that the IB method is first order accurate in the L1 norm. But almost no rigorous proof could be found in the literature until recently [14] in which the author showed that the velocity is indeed first order accurate for the Stokes equations with a periodic boundary condition. In this paper, we show first order convergence with a log h factor of the IB method for elliptic interface problems essentially without the boundary condition restrictions. The results should be applicable to the IB method for many different situations involving elliptic solvers for Stokes and Navier-Stokes equations. keywords: Immersed Boundary (IB) method, Dirac delta function, convergence of IB method, discrete Green function, discrete Green's formula. AMS Subject Classification 2000 65M12, 65M20. 1 Introduction Since its invention in 1970's, the Immersed Boundary (IB) method [15] has been applied almost everywhere in mathematics, engineering, biology, fluid mechanics, and many many more areas, see for example, [16] for a review and references therein. The IB method is not only a mathematical modeling tool in which a complicated boundary condition can be treated as a source distribution but also a numerical method in which a discrete delta function is used.
    [Show full text]