Vector Space Theory
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

On the Bicoset of a Bivector Space
International J.Math. Combin. Vol.4 (2009), 01-08 On the Bicoset of a Bivector Space Agboola A.A.A.† and Akinola L.S.‡ † Department of Mathematics, University of Agriculture, Abeokuta, Nigeria ‡ Department of Mathematics and computer Science, Fountain University, Osogbo, Nigeria E-mail: [email protected], [email protected] Abstract: The study of bivector spaces was first intiated by Vasantha Kandasamy in [1]. The objective of this paper is to present the concept of bicoset of a bivector space and obtain some of its elementary properties. Key Words: bigroup, bivector space, bicoset, bisum, direct bisum, inner biproduct space, biprojection. AMS(2000): 20Kxx, 20L05. §1. Introduction and Preliminaries The study of bialgebraic structures is a new development in the field of abstract algebra. Some of the bialgebraic structures already developed and studied and now available in several literature include: bigroups, bisemi-groups, biloops, bigroupoids, birings, binear-rings, bisemi- rings, biseminear-rings, bivector spaces and a host of others. Since the concept of bialgebraic structure is pivoted on the union of two non-empty subsets of a given algebraic structure for example a group, the usual problem arising from the union of two substructures of such an algebraic structure which generally do not form any algebraic structure has been resolved. With this new concept, several interesting algebraic properties could be obtained which are not present in the parent algebraic structure. In [1], Vasantha Kandasamy initiated the study of bivector spaces. Further studies on bivector spaces were presented by Vasantha Kandasamy and others in [2], [4] and [5]. In the present work however, we look at the bicoset of a bivector space and obtain some of its elementary properties. -

Field Theory Pete L. Clark
Field Theory Pete L. Clark Thanks to Asvin Gothandaraman and David Krumm for pointing out errors in these notes. Contents About These Notes 7 Some Conventions 9 Chapter 1. Introduction to Fields 11 Chapter 2. Some Examples of Fields 13 1. Examples From Undergraduate Mathematics 13 2. Fields of Fractions 14 3. Fields of Functions 17 4. Completion 18 Chapter 3. Field Extensions 23 1. Introduction 23 2. Some Impossible Constructions 26 3. Subfields of Algebraic Numbers 27 4. Distinguished Classes 29 Chapter 4. Normal Extensions 31 1. Algebraically closed fields 31 2. Existence of algebraic closures 32 3. The Magic Mapping Theorem 35 4. Conjugates 36 5. Splitting Fields 37 6. Normal Extensions 37 7. The Extension Theorem 40 8. Isaacs' Theorem 40 Chapter 5. Separable Algebraic Extensions 41 1. Separable Polynomials 41 2. Separable Algebraic Field Extensions 44 3. Purely Inseparable Extensions 46 4. Structural Results on Algebraic Extensions 47 Chapter 6. Norms, Traces and Discriminants 51 1. Dedekind's Lemma on Linear Independence of Characters 51 2. The Characteristic Polynomial, the Trace and the Norm 51 3. The Trace Form and the Discriminant 54 Chapter 7. The Primitive Element Theorem 57 1. The Alon-Tarsi Lemma 57 2. The Primitive Element Theorem and its Corollary 57 3 4 CONTENTS Chapter 8. Galois Extensions 61 1. Introduction 61 2. Finite Galois Extensions 63 3. An Abstract Galois Correspondence 65 4. The Finite Galois Correspondence 68 5. The Normal Basis Theorem 70 6. Hilbert's Theorem 90 72 7. Infinite Algebraic Galois Theory 74 8. A Characterization of Normal Extensions 75 Chapter 9. -

Introduction to Linear Bialgebra
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by University of New Mexico University of New Mexico UNM Digital Repository Mathematics and Statistics Faculty and Staff Publications Academic Department Resources 2005 INTRODUCTION TO LINEAR BIALGEBRA Florentin Smarandache University of New Mexico, [email protected] W.B. Vasantha Kandasamy K. Ilanthenral Follow this and additional works at: https://digitalrepository.unm.edu/math_fsp Part of the Algebra Commons, Analysis Commons, Discrete Mathematics and Combinatorics Commons, and the Other Mathematics Commons Recommended Citation Smarandache, Florentin; W.B. Vasantha Kandasamy; and K. Ilanthenral. "INTRODUCTION TO LINEAR BIALGEBRA." (2005). https://digitalrepository.unm.edu/math_fsp/232 This Book is brought to you for free and open access by the Academic Department Resources at UNM Digital Repository. It has been accepted for inclusion in Mathematics and Statistics Faculty and Staff Publications by an authorized administrator of UNM Digital Repository. For more information, please contact [email protected], [email protected], [email protected]. INTRODUCTION TO LINEAR BIALGEBRA W. B. Vasantha Kandasamy Department of Mathematics Indian Institute of Technology, Madras Chennai – 600036, India e-mail: [email protected] web: http://mat.iitm.ac.in/~wbv Florentin Smarandache Department of Mathematics University of New Mexico Gallup, NM 87301, USA e-mail: [email protected] K. Ilanthenral Editor, Maths Tiger, Quarterly Journal Flat No.11, Mayura Park, 16, Kazhikundram Main Road, Tharamani, Chennai – 600 113, India e-mail: [email protected] HEXIS Phoenix, Arizona 2005 1 This book can be ordered in a paper bound reprint from: Books on Demand ProQuest Information & Learning (University of Microfilm International) 300 N. -
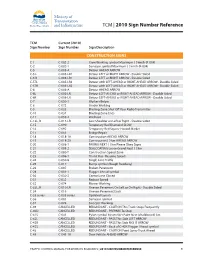
2010 Sign Number Reference for Traffic Control Manual
TCM | 2010 Sign Number Reference TCM Current (2010) Sign Number Sign Number Sign Description CONSTRUCTION SIGNS C-1 C-002-2 Crew Working symbol Maximum ( ) km/h (R-004) C-2 C-002-1 Surveyor symbol Maximum ( ) km/h (R-004) C-5 C-005-A Detour AHEAD ARROW C-5 L C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5 R C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5TL C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-5TR C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6 C-006-A Detour AHEAD ARROW C-6L C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6R C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-7 C-050-1 Workers Below C-8 C-072 Grader Working C-9 C-033 Blasting Zone Shut Off Your Radio Transmitter C-10 C-034 Blasting Zone Ends C-11 C-059-2 Washout C-13L, R C-013-LR Low Shoulder on Left or Right - Double Sided C-15 C-090 Temporary Red Diamond SLOW C-16 C-092 Temporary Red Square Hazard Marker C-17 C-051 Bridge Repair C-18 C-018-1A Construction AHEAD ARROW C-19 C-018-2A Construction ( ) km AHEAD ARROW C-20 C-008-1 PAVING NEXT ( ) km Please Obey Signs C-21 C-008-2 SEALCOATING Loose Gravel Next ( ) km C-22 C-080-T Construction Speed Zone C-23 C-086-1 Thank You - Resume Speed C-24 C-030-8 Single Lane Traffic C-25 C-017 Bump symbol (Rough Roadway) C-26 C-007 Broken Pavement C-28 C-001-1 Flagger Ahead symbol C-30 C-030-2 Centre Lane Closed C-31 C-032 Reduce Speed C-32 C-074 Mower Working C-33L, R C-010-LR Uneven Pavement On Left or On Right - Double Sided C-34 -

Geometry on Grassmannians and Applications to Splitting Bundles and Smoothing Cycles
PUBLICATIONS MATHÉMATIQUES DE L’I.H.É.S. STEVEN L. KLEIMAN Geometry on grassmannians and applications to splitting bundles and smoothing cycles Publications mathématiques de l’I.H.É.S., tome 36 (1969), p. 281-297. <http://www.numdam.org/item?id=PMIHES_1969__36__281_0> © Publications mathématiques de l’I.H.É.S., 1969, tous droits réservés. L’accès aux archives de la revue « Publications mathématiques de l’I.H.É.S. » (http://www. ihes.fr/IHES/Publications/Publications.html), implique l’accord avec les conditions générales d’utilisation (http://www.numdam.org/legal.php). Toute utilisation commerciale ou impression systématique est constitutive d’une infraction pénale. Toute copie ou impression de ce fi- chier doit contenir la présente mention de copyright. Article numérisé dans le cadre du programme Numérisation de documents anciens mathématiques http://www.numdam.org/ GEOMETRY ON GRASSMANNIANS AND APPLICATIONS TO SPLITTING BUNDLES AND SMOOTHING CYCLES by STEVEN L. KLEIMAN (1) INTRODUCTION Let k be an algebraically closed field, V a smooth ^-dimensional subscheme of projective space over A:, and consider the following problems: Problem 1 (splitting bundles). — Given a (vector) bundle G on V, find a monoidal transformation f \ V'->V with smooth center CT such thatyG contains a line bundle P. Problem 2 (smoothing cycles). — Given a cycle Z on V, deform Z by rational equivalence into the difference Z^ — Zg of two effective cycles whose prime components are all smooth. Strengthened form. — Given any finite number of irreducible subschemes V, of V, choose a (resp. Z^, Zg) such that for all i, the intersection V^n a (resp. -

THE DIMENSION of a VECTOR SPACE 1. Introduction This Handout
THE DIMENSION OF A VECTOR SPACE KEITH CONRAD 1. Introduction This handout is a supplementary discussion leading up to the definition of dimension of a vector space and some of its properties. We start by defining the span of a finite set of vectors and linear independence of a finite set of vectors, which are combined to define the all-important concept of a basis. Definition 1.1. Let V be a vector space over a field F . For any finite subset fv1; : : : ; vng of V , its span is the set of all of its linear combinations: Span(v1; : : : ; vn) = fc1v1 + ··· + cnvn : ci 2 F g: Example 1.2. In F 3, Span((1; 0; 0); (0; 1; 0)) is the xy-plane in F 3. Example 1.3. If v is a single vector in V then Span(v) = fcv : c 2 F g = F v is the set of scalar multiples of v, which for nonzero v should be thought of geometrically as a line (through the origin, since it includes 0 · v = 0). Since sums of linear combinations are linear combinations and the scalar multiple of a linear combination is a linear combination, Span(v1; : : : ; vn) is a subspace of V . It may not be all of V , of course. Definition 1.4. If fv1; : : : ; vng satisfies Span(fv1; : : : ; vng) = V , that is, if every vector in V is a linear combination from fv1; : : : ; vng, then we say this set spans V or it is a spanning set for V . Example 1.5. In F 2, the set f(1; 0); (0; 1); (1; 1)g is a spanning set of F 2. -

Bases for Infinite Dimensional Vector Spaces Math 513 Linear Algebra Supplement
BASES FOR INFINITE DIMENSIONAL VECTOR SPACES MATH 513 LINEAR ALGEBRA SUPPLEMENT Professor Karen E. Smith We have proven that every finitely generated vector space has a basis. But what about vector spaces that are not finitely generated, such as the space of all continuous real valued functions on the interval [0; 1]? Does such a vector space have a basis? By definition, a basis for a vector space V is a linearly independent set which generates V . But we must be careful what we mean by linear combinations from an infinite set of vectors. The definition of a vector space gives us a rule for adding two vectors, but not for adding together infinitely many vectors. By successive additions, such as (v1 + v2) + v3, it makes sense to add any finite set of vectors, but in general, there is no way to ascribe meaning to an infinite sum of vectors in a vector space. Therefore, when we say that a vector space V is generated by or spanned by an infinite set of vectors fv1; v2;::: g, we mean that each vector v in V is a finite linear combination λi1 vi1 + ··· + λin vin of the vi's. Likewise, an infinite set of vectors fv1; v2;::: g is said to be linearly independent if the only finite linear combination of the vi's that is zero is the trivial linear combination. So a set fv1; v2; v3;:::; g is a basis for V if and only if every element of V can be be written in a unique way as a finite linear combination of elements from the set. -

Glossary of Linear Algebra Terms
INNER PRODUCT SPACES AND THE GRAM-SCHMIDT PROCESS A. HAVENS 1. The Dot Product and Orthogonality 1.1. Review of the Dot Product. We first recall the notion of the dot product, which gives us a familiar example of an inner product structure on the real vector spaces Rn. This product is connected to the Euclidean geometry of Rn, via lengths and angles measured in Rn. Later, we will introduce inner product spaces in general, and use their structure to define general notions of length and angle on other vector spaces. Definition 1.1. The dot product of real n-vectors in the Euclidean vector space Rn is the scalar product · : Rn × Rn ! R given by the rule n n ! n X X X (u; v) = uiei; viei 7! uivi : i=1 i=1 i n Here BS := (e1;:::; en) is the standard basis of R . With respect to our conventions on basis and matrix multiplication, we may also express the dot product as the matrix-vector product 2 3 v1 6 7 t î ó 6 . 7 u v = u1 : : : un 6 . 7 : 4 5 vn It is a good exercise to verify the following proposition. Proposition 1.1. Let u; v; w 2 Rn be any real n-vectors, and s; t 2 R be any scalars. The Euclidean dot product (u; v) 7! u · v satisfies the following properties. (i:) The dot product is symmetric: u · v = v · u. (ii:) The dot product is bilinear: • (su) · v = s(u · v) = u · (sv), • (u + v) · w = u · w + v · w. -

MTH 304: General Topology Semester 2, 2017-2018
MTH 304: General Topology Semester 2, 2017-2018 Dr. Prahlad Vaidyanathan Contents I. Continuous Functions3 1. First Definitions................................3 2. Open Sets...................................4 3. Continuity by Open Sets...........................6 II. Topological Spaces8 1. Definition and Examples...........................8 2. Metric Spaces................................. 11 3. Basis for a topology.............................. 16 4. The Product Topology on X × Y ...................... 18 Q 5. The Product Topology on Xα ....................... 20 6. Closed Sets.................................. 22 7. Continuous Functions............................. 27 8. The Quotient Topology............................ 30 III.Properties of Topological Spaces 36 1. The Hausdorff property............................ 36 2. Connectedness................................. 37 3. Path Connectedness............................. 41 4. Local Connectedness............................. 44 5. Compactness................................. 46 6. Compact Subsets of Rn ............................ 50 7. Continuous Functions on Compact Sets................... 52 8. Compactness in Metric Spaces........................ 56 9. Local Compactness.............................. 59 IV.Separation Axioms 62 1. Regular Spaces................................ 62 2. Normal Spaces................................ 64 3. Tietze's extension Theorem......................... 67 4. Urysohn Metrization Theorem........................ 71 5. Imbedding of Manifolds.......................... -

General Topology
General Topology Tom Leinster 2014{15 Contents A Topological spaces2 A1 Review of metric spaces.......................2 A2 The definition of topological space.................8 A3 Metrics versus topologies....................... 13 A4 Continuous maps........................... 17 A5 When are two spaces homeomorphic?................ 22 A6 Topological properties........................ 26 A7 Bases................................. 28 A8 Closure and interior......................... 31 A9 Subspaces (new spaces from old, 1)................. 35 A10 Products (new spaces from old, 2)................. 39 A11 Quotients (new spaces from old, 3)................. 43 A12 Review of ChapterA......................... 48 B Compactness 51 B1 The definition of compactness.................... 51 B2 Closed bounded intervals are compact............... 55 B3 Compactness and subspaces..................... 56 B4 Compactness and products..................... 58 B5 The compact subsets of Rn ..................... 59 B6 Compactness and quotients (and images)............. 61 B7 Compact metric spaces........................ 64 C Connectedness 68 C1 The definition of connectedness................... 68 C2 Connected subsets of the real line.................. 72 C3 Path-connectedness.......................... 76 C4 Connected-components and path-components........... 80 1 Chapter A Topological spaces A1 Review of metric spaces For the lecture of Thursday, 18 September 2014 Almost everything in this section should have been covered in Honours Analysis, with the possible exception of some of the examples. For that reason, this lecture is longer than usual. Definition A1.1 Let X be a set. A metric on X is a function d: X × X ! [0; 1) with the following three properties: • d(x; y) = 0 () x = y, for x; y 2 X; • d(x; y) + d(y; z) ≥ d(x; z) for all x; y; z 2 X (triangle inequality); • d(x; y) = d(y; x) for all x; y 2 X (symmetry). -

Convolution.Pdf
Convolution March 22, 2020 0.0.1 Setting up [23]: from bokeh.plotting import figure from bokeh.io import output_notebook, show,curdoc from bokeh.themes import Theme import numpy as np output_notebook() theme=Theme(json={}) curdoc().theme=theme 0.1 Convolution Convolution is a fundamental operation that appears in many different contexts in both pure and applied settings in mathematics. Polynomials: a simple case Let’s look at a simple case first. Consider the space of real valued polynomial functions P. If f 2 P, we have X1 i f(z) = aiz i=0 where ai = 0 for i sufficiently large. There is an obvious linear map a : P! c00(R) where c00(R) is the space of sequences that are eventually zero. i For each integer i, we have a projection map ai : c00(R) ! R so that ai(f) is the coefficient of z for f 2 P. Since P is a ring under addition and multiplication of functions, these operations must be reflected on the other side of the map a. 1 Clearly we can add sequences in c00(R) componentwise, and since addition of polynomials is also componentwise we have: a(f + g) = a(f) + a(g) What about multiplication? We know that X Xn X1 an(fg) = ar(f)as(g) = ar(f)an−r(g) = ar(f)an−r(g) r+s=n r=0 r=0 where we adopt the convention that ai(f) = 0 if i < 0. Given (a0; a1;:::) and (b0; b1;:::) in c00(R), define a ∗ b = (c0; c1;:::) where X1 cn = ajbn−j j=0 with the same convention that ai = bi = 0 if i < 0. -

Calculus Terminology
AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential