Airfoils and Wings
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Glossary Physics (I-Introduction)
1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay. -

Airfoil Drag by Wake Survey Using Ldv
AIRFOIL DRAG BY WAKE SURVEY USING LDV 1 Purpose This experiment introduces the student to the use of Laser Doppler Velocimetry (LDV) as a means of measuring air flow velocities. The section drag of a NACA 0012 airfoil is determined from velocity measurements obtained in the airfoil wake. 2 Apparatus (1) .5 m x .7 m wind tunnel (max velocity 20 m/s) (2) NACA 0015 airfoil (0.2 m chord, 0.7 m span) (3) Betz manometer (4) Pitot tube (5) DISA LDV optics (6) Spectra Physics 124B 15 mW laser (632.8 nm) (7) DISA 55N20 LDV frequency tracker (8) TSI atomizer using 50cs silicone oil (9) XYZ LDV traversing system (10) Computer data reduction program 1 3 Notation A wing area (m2) b initial laser beam radius (m) bo minimum laser beam radius at lens focus (m) c airfoil chord length (m) Cd drag coefficient da elemental area in wake survey plane (m2) d drag force per unit span f focal length of primary lens (m) fo Doppler frequency (Hz) I detected signal amplitude (V) l distance across survey plane (m) r seed particle radius (m) s airfoil span (m) v seed particle velocity (instantaneous flow velocity) (m/s) U wake velocity (m/s) Uo upstream flow velocity (m/s) α Mie scatter size parameter/angle of attack (degs) δy fringe separation (m) θ intersection angle of laser beams λ laser wavelength (632.8 nm for He Ne laser) ρ air density at NTP (1.225 kg/m3) τ Doppler period (s) 4 Theory 4.1 Introduction The profile drag of a two-dimensional airfoil is the sum of the form drag due to boundary layer sep- aration (pressure drag), and the skin friction drag. -
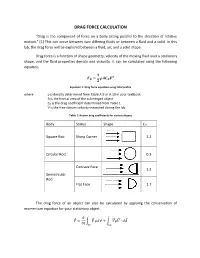
Drag Force Calculation
DRAG FORCE CALCULATION “Drag is the component of force on a body acting parallel to the direction of relative motion.” [1] This can occur between two differing fluids or between a fluid and a solid. In this lab, the drag force will be explored between a fluid, air, and a solid shape. Drag force is a function of shape geometry, velocity of the moving fluid over a stationary shape, and the fluid properties density and viscosity. It can be calculated using the following equation, ퟏ 푭 = 흆푨푪 푽ퟐ 푫 ퟐ 푫 Equation 1: Drag force equation using total profile where ρ is density determined from Table A.9 or A.10 in your textbook A is the frontal area of the submerged object CD is the drag coefficient determined from Table 1 V is the free-stream velocity measured during the lab Table 1: Known drag coefficients for various shapes Body Status Shape CD Square Rod Sharp Corner 2.2 Circular Rod 0.3 Concave Face 1.2 Semicircular Rod Flat Face 1.7 The drag force of an object can also be calculated by applying the conservation of momentum equation for your stationary object. 휕 퐹⃗ = ∫ 푉⃗⃗ 휌푑∀ + ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 휕푡 퐶푉 퐶푆 Assuming steady flow, the equation reduces to 퐹⃗ = ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 퐶푆 The following frontal view of the duct is shown below. Integrating the velocity profile after the shape will allow calculation of drag force per unit span. Figure 1: Velocity profile after an inserted shape. Combining the previous equation with Figure 1, the following equation is obtained: 푊 퐷푓 = ∫ 휌푈푖(푈∞ − 푈푖)퐿푑푦 0 Simplifying the equation, you get: 20 퐷푓 = 휌퐿 ∑ 푈푖(푈∞ − 푈푖)훥푦 푖=1 Equation 2: Drag force equation using wake profile The pressure measurements can be converted into velocity using the Bernoulli’s equation as follows: 2Δ푃푖 푈푖 = √ 휌퐴푖푟 Be sure to remember that the manometers used are in W.C. -

Chapter 4: Immersed Body Flow [Pp
MECH 3492 Fluid Mechanics and Applications Univ. of Manitoba Fall Term, 2017 Chapter 4: Immersed Body Flow [pp. 445-459 (8e), or 374-386 (9e)] Dr. Bing-Chen Wang Dept. of Mechanical Engineering Univ. of Manitoba, Winnipeg, MB, R3T 5V6 When a viscous fluid flow passes a solid body (fully-immersed in the fluid), the body experiences a net force, F, which can be decomposed into two components: a drag force F , which is parallel to the flow direction, and • D a lift force F , which is perpendicular to the flow direction. • L The drag coefficient CD and lift coefficient CL are defined as follows: FD FL CD = 1 2 and CL = 1 2 , (112) 2 ρU A 2 ρU Ap respectively. Here, U is the free-stream velocity, A is the “wetted area” (total surface area in contact with fluid), and Ap is the “planform area” (maximum projected area of an object such as a wing). In the remainder of this section, we focus our attention on the drag forces. As discussed previously, there are two types of drag forces acting on a solid body immersed in a viscous flow: friction drag (also called “viscous drag”), due to the wall friction shear stress exerted on the • surface of a solid body; pressure drag (also called “form drag”), due to the difference in the pressure exerted on the front • and rear surfaces of a solid body. The friction drag and pressure drag on a finite immersed body are defined as FD,vis = τwdA and FD, pres = pdA , (113) ZA ZA Streamwise component respectively. -

Drag Coefficients of Inclined Hollow Cylinders
Drag Coefficients of Inclined Hollow Cylinders: RANS versus LES A Major Qualifying Project Report Submitted to the Faculty of the WORCESTER POLYTECHNIC INSTITUTE in partial fulfillment of the requirements for the Degree of Bachelor of Science In Chemical Engineering By Ben Franzluebbers _______________ Date: April 2013 Approved: ________________________ Dr. Anthony G. Dixon, Advisor Abstract The goal of this project was use LES and RANS (SST k-ω) CFD turbulence models to find the drag coefficient of a hollow cylinder at various inclinations and compare the results. The drag coefficients were evaluated for three angles relative to the flow (0⁰, 45⁰, and 90⁰) and three Reynolds numbers (1000, 5000, and 10000). The drag coefficients determined by LES and RANS agreed for the 0⁰ and 90⁰ inclined hollow cylinder. For the 45⁰ inclined hollow cylinder the RANS model predicted drag coefficients about 0.2 lower the drag coefficients predicted by LES. 2 Executive Summary The design of catalyst particles is an important topic in the chemical industry. Chemical products made using catalytic processes are worth $900 billion a year and about 75% of all chemical and petroleum products by value (U.S. Climate Change Technology Program, 2005). The catalyst particles used for fixed bed reactors are an important part of this. Knowing properties of the catalyst particle such as the drag coefficient is necessary to understand how fluid flow will be affected by the packed bed. The particles are inclined at different angles in the reactor and can come in a wide variety of shapes meaning that understanding the effect of particle shape on drag coefficient has practical importance. -

On the Generation of a Reverse Von Kármán Street for the Controlled Cylinder Wake in the Laminar Regime
On the generation of a reverse Von Kármán street for the controlled cylinder wake in the laminar regime Michel Bergmann,∗ Laurent Cordier, and Jean-Pierre Brancher LEMTA, UMR 7563 (CNRS - INPL - UHP) ENSEM - 2, avenue de la forêt de Haye BP 160 - 54504 Vandœuvre cedex, France (Dated: December 8, 2005) 1 Abstract In this Brief Communication we are interested in the maximum mean drag reduction that can be achieved under rotary sinusoidal control for the circular cylinder wake in the laminar regime. For a Reynolds number equal to 200, we give numerical evidence that partial control restricted to an upstream part of the cylinder surface may increase considerably the effectiveness of the control. Indeed, a maximum value of relative mean drag reduction equal to 30% is obtained when applying a specific sinusoidal control to the whole cylinder, where up to 75% of reduction can be obtained when the same control law is applied only to a well selected upstream part of the cylinder. This result suggests that a mean flow correction field with negative drag is observable for this controlled flow configuration. The significant thrust force that is locally generated in the near wake corresponds to a reverse Kármán vortex street as commonly observed in fish-like locomotion or flapping wing flight. Finally, the energetic efficiency of the control is quantified by examining the Power Saving Ratio: it is shown that our approach is energetically inefficient. However, it is also demonstrated that for this control scheme the improvement of the effectiveness goes generally with an improvement of the efficiency. Keywords: Partial rotary control ; Cylinder wake ; Drag minimization ; reverse Kármán vortex street. -

Aerodynamics of High-Performance Wing Sails
Aerodynamics of High-Performance Wing Sails J. otto Scherer^ Some of tfie primary requirements for tiie design of wing sails are discussed. In particular, ttie requirements for maximizing thrust when sailing to windward and tacking downwind are presented. The results of water channel tests on six sail section shapes are also presented. These test results Include the data for the double-slotted flapped wing sail designed by David Hubbard for A. F. Dl Mauro's lYRU "C" class catamaran Patient Lady II. Introduction The propulsion system is probably the single most neglect ed area of yacht design. The conventional triangular "soft" sails, while simple, practical, and traditional, are a long way from being aerodynamically desirable. The aerodynamic driving force of the sails is, of course, just as large and just as important as the hydrodynamic resistance of the hull. Yet, designers will go to great lengths to fair hull lines and tank test hull shapes, while simply drawing a triangle on the plans to define the sails. There is no question in my mind that the application of the wealth of available airfoil technology will yield enormous gains in yacht performance when applied to sail design. Re cent years have seen the application of some of this technolo gy in the form of wing sails on the lYRU "C" class catamar ans. In this paper, I will review some of the aerodynamic re quirements of yacht sails which have led to the development of the wing sails. For purposes of discussion, we can divide sail require ments into three points of sailing: • Upwind and close reaching. -

UNIT – 4 FORCES on IMMERSED BODIES Lecture-01
1 UNIT – 4 FORCES ON IMMERSED BODIES Lecture-01 Forces on immersed bodies When a body is immersed in a real fluid, which is flowing at a uniform velocity U, the fluid will exert a force on the body. The total force (FR) can be resolved in two components: 1. Drag (FD): Component of the total force in the direction of motion of fluid. 2. Lift (FL): Component of the total force in the perpendicular direction of the motion of fluid. It occurs only when the axis of the body is inclined to the direction of fluid flow. If the axis of the body is parallel to the fluid flow, lift force will be zero. Expression for Drag & Lift Forces acting on the small elemental area dA are: i. Pressure force acting perpendicular to the surface i.e. p dA ii. Shear force acting along the tangential direction to the surface i.e. τ0dA (a) Drag force (FD) : Drag force on elemental area = p dAcosθ + τ0 dAcos(90 – θ = p dAosθ + τ0dAsinθ Hence Total drag (or profile drag) is given by, Where �� = ∫ � cos � �� + ∫�0 sin � �� = pressure drag or form drag, and ∫ � cos � �� = shear drag or friction drag or skin drag (b) Lift0 force (F ) : ∫ � sin � ��L Lift force on the elemental area = − p dAsinθ + τ0 dA sin(90 – θ = − p dAsiθ + τ0dAcosθ Hence, total lift is given by http://www.rgpvonline.com �� = ∫�0 cos � �� − ∫ p sin � �� 2 The drag & lift for a body moving in a fluid of density at a uniform velocity U are calculated mathematically as 2 � And �� = � � � 2 � Where A = projected area of the body or�� largest= � project� � area of the immersed body. -

Chapter 4: Immersed Body Flow [Pp
MECH 3492 Fluid Mechanics and Applications Univ. of Manitoba Fall Term, 2017 Chapter 4: Immersed Body Flow [pp. 445-459 (8e), or 374-386 (9e)] Dr. Bing-Chen Wang Dept. of Mechanical Engineering Univ. of Manitoba, Winnipeg, MB, R3T 5V6 When a viscous fluid flow passes a solid body (fully-immersed in the fluid), the body experiences a net force, F, which can be decomposed into two components: a drag force F , which is parallel to the flow direction, and • D a lift force F , which is perpendicular to the flow direction. • L The drag coefficient CD and lift coefficient CL are defined as follows: FD FL CD = 1 2 and CL = 1 2 , (112) 2 ρU A 2 ρU Ap respectively. Here, U is the free-stream velocity, A is the “wetted area” (total surface area in contact with fluid), and Ap is the “planform area” (maximum projected area of an object such as a wing). In the remainder of this section, we focus our attention on the drag forces. As discussed previously, there are two types of drag forces acting on a solid body immersed in a viscous flow: friction drag (also called “viscous drag”), due to the wall friction shear stress exerted on the • surface of a solid body; pressure drag (also called “form drag”), due to the difference in the pressure exerted on the front • and rear surfaces of a solid body. The friction drag and pressure drag on a finite immersed body are defined as FD,vis = τwdA and FD, pres = pdA , (113) ZA ZA Streamwise component respectively. -

Upwind Sail Aerodynamics : a RANS Numerical Investigation Validated with Wind Tunnel Pressure Measurements I.M Viola, Patrick Bot, M
Upwind sail aerodynamics : A RANS numerical investigation validated with wind tunnel pressure measurements I.M Viola, Patrick Bot, M. Riotte To cite this version: I.M Viola, Patrick Bot, M. Riotte. Upwind sail aerodynamics : A RANS numerical investigation validated with wind tunnel pressure measurements. International Journal of Heat and Fluid Flow, Elsevier, 2012, 39, pp.90-101. 10.1016/j.ijheatfluidflow.2012.10.004. hal-01071323 HAL Id: hal-01071323 https://hal.archives-ouvertes.fr/hal-01071323 Submitted on 8 Oct 2014 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. I.M. Viola, P. Bot, M. Riotte Upwind Sail Aerodynamics: a RANS numerical investigation validated with wind tunnel pressure measurements International Journal of Heat and Fluid Flow 39 (2013) 90–101 http://dx.doi.org/10.1016/j.ijheatfluidflow.2012.10.004 Keywords: sail aerodynamics, CFD, RANS, yacht, laminar separation bubble, viscous drag. Abstract The aerodynamics of a sailing yacht with different sail trims are presented, derived from simulations performed using Computational Fluid Dynamics. A Reynolds-averaged Navier- Stokes approach was used to model sixteen sail trims first tested in a wind tunnel, where the pressure distributions on the sails were measured. -

Hydraulics Manual Glossary G - 3
Glossary G - 1 GLOSSARY OF HIGHWAY-RELATED DRAINAGE TERMS (Reprinted from the 1999 edition of the American Association of State Highway and Transportation Officials Model Drainage Manual) G.1 Introduction This Glossary is divided into three parts: · Introduction, · Glossary, and · References. It is not intended that all the terms in this Glossary be rigorously accurate or complete. Realistically, this is impossible. Depending on the circumstance, a particular term may have several meanings; this can never change. The primary purpose of this Glossary is to define the terms found in the Highway Drainage Guidelines and Model Drainage Manual in a manner that makes them easier to interpret and understand. A lesser purpose is to provide a compendium of terms that will be useful for both the novice as well as the more experienced hydraulics engineer. This Glossary may also help those who are unfamiliar with highway drainage design to become more understanding and appreciative of this complex science as well as facilitate communication between the highway hydraulics engineer and others. Where readily available, the source of a definition has been referenced. For clarity or format purposes, cited definitions may have some additional verbiage contained in double brackets [ ]. Conversely, three “dots” (...) are used to indicate where some parts of a cited definition were eliminated. Also, as might be expected, different sources were found to use different hyphenation and terminology practices for the same words. Insignificant changes in this regard were made to some cited references and elsewhere to gain uniformity for the terms contained in this Glossary: as an example, “groundwater” vice “ground-water” or “ground water,” and “cross section area” vice “cross-sectional area.” Cited definitions were taken primarily from two sources: W.B. -

List of Symbols
List of Symbols a atmosphere speed of sound a exponent in approximate thrust formula ac aerodynamic center a acceleration vector a0 airfoil angle of attack for zero lift A aspect ratio A system matrix A aerodynamic force vector b span b exponent in approximate SFC formula c chord cd airfoil drag coefficient cl airfoil lift coefficient clα airfoil lift curve slope cmac airfoil pitching moment about the aerodynamic center cr root chord ct tip chord c¯ mean aerodynamic chord C specfic fuel consumption Cc corrected specfic fuel consumption CD drag coefficient CDf friction drag coefficient CDi induced drag coefficient CDw wave drag coefficient CD0 zero-lift drag coefficient Cf skin friction coefficient CF compressibility factor CL lift coefficient CLα lift curve slope CLmax maximum lift coefficient Cmac pitching moment about the aerodynamic center CT nondimensional thrust T Cm nondimensional thrust moment CW nondimensional weight d diameter det determinant D drag e Oswald’s efficiency factor E origin of ground axes system E aerodynamic efficiency or lift to drag ratio EO position vector f flap f factor f equivalent parasite area F distance factor FS stick force F force vector F F form factor g acceleration of gravity g acceleration of gravity vector gs acceleration of gravity at sea level g1 function in Mach number for drag divergence g2 function in Mach number for drag divergence H elevator hinge moment G time factor G elevator gearing h altitude above sea level ht altitude of the tropopause hH height of HT ac above wingc ¯ h˙ rate of climb 2 i unit vector iH horizontal