List of Symbols
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Glossary Physics (I-Introduction)
1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay. -

Airfoil Drag by Wake Survey Using Ldv
AIRFOIL DRAG BY WAKE SURVEY USING LDV 1 Purpose This experiment introduces the student to the use of Laser Doppler Velocimetry (LDV) as a means of measuring air flow velocities. The section drag of a NACA 0012 airfoil is determined from velocity measurements obtained in the airfoil wake. 2 Apparatus (1) .5 m x .7 m wind tunnel (max velocity 20 m/s) (2) NACA 0015 airfoil (0.2 m chord, 0.7 m span) (3) Betz manometer (4) Pitot tube (5) DISA LDV optics (6) Spectra Physics 124B 15 mW laser (632.8 nm) (7) DISA 55N20 LDV frequency tracker (8) TSI atomizer using 50cs silicone oil (9) XYZ LDV traversing system (10) Computer data reduction program 1 3 Notation A wing area (m2) b initial laser beam radius (m) bo minimum laser beam radius at lens focus (m) c airfoil chord length (m) Cd drag coefficient da elemental area in wake survey plane (m2) d drag force per unit span f focal length of primary lens (m) fo Doppler frequency (Hz) I detected signal amplitude (V) l distance across survey plane (m) r seed particle radius (m) s airfoil span (m) v seed particle velocity (instantaneous flow velocity) (m/s) U wake velocity (m/s) Uo upstream flow velocity (m/s) α Mie scatter size parameter/angle of attack (degs) δy fringe separation (m) θ intersection angle of laser beams λ laser wavelength (632.8 nm for He Ne laser) ρ air density at NTP (1.225 kg/m3) τ Doppler period (s) 4 Theory 4.1 Introduction The profile drag of a two-dimensional airfoil is the sum of the form drag due to boundary layer sep- aration (pressure drag), and the skin friction drag. -
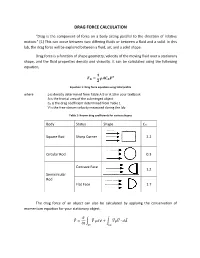
Drag Force Calculation
DRAG FORCE CALCULATION “Drag is the component of force on a body acting parallel to the direction of relative motion.” [1] This can occur between two differing fluids or between a fluid and a solid. In this lab, the drag force will be explored between a fluid, air, and a solid shape. Drag force is a function of shape geometry, velocity of the moving fluid over a stationary shape, and the fluid properties density and viscosity. It can be calculated using the following equation, ퟏ 푭 = 흆푨푪 푽ퟐ 푫 ퟐ 푫 Equation 1: Drag force equation using total profile where ρ is density determined from Table A.9 or A.10 in your textbook A is the frontal area of the submerged object CD is the drag coefficient determined from Table 1 V is the free-stream velocity measured during the lab Table 1: Known drag coefficients for various shapes Body Status Shape CD Square Rod Sharp Corner 2.2 Circular Rod 0.3 Concave Face 1.2 Semicircular Rod Flat Face 1.7 The drag force of an object can also be calculated by applying the conservation of momentum equation for your stationary object. 휕 퐹⃗ = ∫ 푉⃗⃗ 휌푑∀ + ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 휕푡 퐶푉 퐶푆 Assuming steady flow, the equation reduces to 퐹⃗ = ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 퐶푆 The following frontal view of the duct is shown below. Integrating the velocity profile after the shape will allow calculation of drag force per unit span. Figure 1: Velocity profile after an inserted shape. Combining the previous equation with Figure 1, the following equation is obtained: 푊 퐷푓 = ∫ 휌푈푖(푈∞ − 푈푖)퐿푑푦 0 Simplifying the equation, you get: 20 퐷푓 = 휌퐿 ∑ 푈푖(푈∞ − 푈푖)훥푦 푖=1 Equation 2: Drag force equation using wake profile The pressure measurements can be converted into velocity using the Bernoulli’s equation as follows: 2Δ푃푖 푈푖 = √ 휌퐴푖푟 Be sure to remember that the manometers used are in W.C. -

Chapter 4: Immersed Body Flow [Pp
MECH 3492 Fluid Mechanics and Applications Univ. of Manitoba Fall Term, 2017 Chapter 4: Immersed Body Flow [pp. 445-459 (8e), or 374-386 (9e)] Dr. Bing-Chen Wang Dept. of Mechanical Engineering Univ. of Manitoba, Winnipeg, MB, R3T 5V6 When a viscous fluid flow passes a solid body (fully-immersed in the fluid), the body experiences a net force, F, which can be decomposed into two components: a drag force F , which is parallel to the flow direction, and • D a lift force F , which is perpendicular to the flow direction. • L The drag coefficient CD and lift coefficient CL are defined as follows: FD FL CD = 1 2 and CL = 1 2 , (112) 2 ρU A 2 ρU Ap respectively. Here, U is the free-stream velocity, A is the “wetted area” (total surface area in contact with fluid), and Ap is the “planform area” (maximum projected area of an object such as a wing). In the remainder of this section, we focus our attention on the drag forces. As discussed previously, there are two types of drag forces acting on a solid body immersed in a viscous flow: friction drag (also called “viscous drag”), due to the wall friction shear stress exerted on the • surface of a solid body; pressure drag (also called “form drag”), due to the difference in the pressure exerted on the front • and rear surfaces of a solid body. The friction drag and pressure drag on a finite immersed body are defined as FD,vis = τwdA and FD, pres = pdA , (113) ZA ZA Streamwise component respectively. -

Notes on Earth Atmospheric Entry for Mars Sample Return Missions
NASA/TP–2006-213486 Notes on Earth Atmospheric Entry for Mars Sample Return Missions Thomas Rivell Ames Research Center, Moffett Field, California September 2006 The NASA STI Program Office . in Profile Since its founding, NASA has been dedicated to the • CONFERENCE PUBLICATION. Collected advancement of aeronautics and space science. The papers from scientific and technical confer- NASA Scientific and Technical Information (STI) ences, symposia, seminars, or other meetings Program Office plays a key part in helping NASA sponsored or cosponsored by NASA. maintain this important role. • SPECIAL PUBLICATION. Scientific, technical, The NASA STI Program Office is operated by or historical information from NASA programs, Langley Research Center, the Lead Center for projects, and missions, often concerned with NASA’s scientific and technical information. The subjects having substantial public interest. NASA STI Program Office provides access to the NASA STI Database, the largest collection of • TECHNICAL TRANSLATION. English- aeronautical and space science STI in the world. language translations of foreign scientific and The Program Office is also NASA’s institutional technical material pertinent to NASA’s mission. mechanism for disseminating the results of its research and development activities. These results Specialized services that complement the STI are published by NASA in the NASA STI Report Program Office’s diverse offerings include creating Series, which includes the following report types: custom thesauri, building customized databases, organizing and publishing research results . even • TECHNICAL PUBLICATION. Reports of providing videos. completed research or a major significant phase of research that present the results of NASA For more information about the NASA STI programs and include extensive data or theoreti- Program Office, see the following: cal analysis. -

Drag Coefficients of Inclined Hollow Cylinders
Drag Coefficients of Inclined Hollow Cylinders: RANS versus LES A Major Qualifying Project Report Submitted to the Faculty of the WORCESTER POLYTECHNIC INSTITUTE in partial fulfillment of the requirements for the Degree of Bachelor of Science In Chemical Engineering By Ben Franzluebbers _______________ Date: April 2013 Approved: ________________________ Dr. Anthony G. Dixon, Advisor Abstract The goal of this project was use LES and RANS (SST k-ω) CFD turbulence models to find the drag coefficient of a hollow cylinder at various inclinations and compare the results. The drag coefficients were evaluated for three angles relative to the flow (0⁰, 45⁰, and 90⁰) and three Reynolds numbers (1000, 5000, and 10000). The drag coefficients determined by LES and RANS agreed for the 0⁰ and 90⁰ inclined hollow cylinder. For the 45⁰ inclined hollow cylinder the RANS model predicted drag coefficients about 0.2 lower the drag coefficients predicted by LES. 2 Executive Summary The design of catalyst particles is an important topic in the chemical industry. Chemical products made using catalytic processes are worth $900 billion a year and about 75% of all chemical and petroleum products by value (U.S. Climate Change Technology Program, 2005). The catalyst particles used for fixed bed reactors are an important part of this. Knowing properties of the catalyst particle such as the drag coefficient is necessary to understand how fluid flow will be affected by the packed bed. The particles are inclined at different angles in the reactor and can come in a wide variety of shapes meaning that understanding the effect of particle shape on drag coefficient has practical importance. -

A Group-Theoretical Classification of Three-Tone and Four-Tone Harmonic Chords3
A GROUP-THEORETICAL CLASSIFICATION OF THREE-TONE AND FOUR-TONE HARMONIC CHORDS JASON K.C. POLAK Abstract. We classify three-tone and four-tone chords based on subgroups of the symmetric group acting on chords contained within a twelve-tone scale. The actions are inversion, major- minor duality, and augmented-diminished duality. These actions correspond to elements of symmetric groups, and also correspond directly to intuitive concepts in the harmony theory of music. We produce a graph of how these actions relate different seventh chords that suggests a concept of distance in the theory of harmony. Contents 1. Introduction 1 Acknowledgements 2 2. Three-tone harmonic chords 2 3. Four-tone harmonic chords 4 4. The chord graph 6 References 8 References 8 1. Introduction Early on in music theory we learn of the harmonic triads: major, minor, augmented, and diminished. Later on we find out about four-note chords such as seventh chords. We wish to describe a classification of these types of chords using the action of the finite symmetric groups. We represent notes by a number in the set Z/12 = {0, 1, 2,..., 10, 11}. Under this scheme, for example, 0 represents C, 1 represents C♯, 2 represents D, and so on. We consider only pitch classes modulo the octave. arXiv:2007.03134v1 [math.GR] 6 Jul 2020 We describe the sounding of simultaneous notes by an ordered increasing list of integers in Z/12 surrounded by parentheses. For example, a major second interval M2 would be repre- sented by (0, 2), and a major chord would be represented by (0, 4, 7). -

Conceptual Design Study of a Hydrogen Powered Ultra Large Cargo Aircraft
Conceptual Design Study of a Hydrogen Powered Ultra Large Cargo Aircraft R.A.J. Jansen University of Technology Technology of University Delft Delft Conceptual Design Study of a Hydrogen Powered Ultra Large Cargo Aircraft Towards a competitive and sustainable alternative of maritime transport by R.A.J. Jansen to obtain the degree of Master of Science at the Delft University of Technology, to be defended publicly on Tuesday January 10, 2017 at 9:00 AM. Student number: 4036093 Thesis registration: 109#17#MT#FPP Project duration: January 11, 2016 – January 10, 2017 Thesis committee: Dr. ir. G. La Rocca, TU Delft, supervisor Dr. A. Gangoli Rao, TU Delft Dr. ir. H. G. Visser, TU Delft An electronic version of this thesis is available at http://repository.tudelft.nl/. Acknowledgements This report presents the research performed to complete the master track Flight Performance and Propulsion at the Technical University of Delft. I am really grateful to the people who supported me both during the master thesis as well as during the rest of my student life. First of all, I would like to thank my supervisor, Gianfranco La Rocca. He supported and motivated me during the entire graduation project and provided valuable feedback during all the status meeting we had. I would also like to thank the exam committee, Arvind Gangoli Rao and Dries Visser, for their flexibility and time to assess my work. Moreover, I would like to thank Ali Elham for his advice throughout the project as well as during the green light meeting. Next to these people, I owe also thanks to the fellow students in room 2.44 for both their advice, as well as the enjoyable chats during the lunch and coffee breaks. -

Airframe Integration
Aerodynamic Design of the Hybrid Wing Body Propulsion- Airframe Integration May-Fun Liou1, Hyoungjin Kim2, ByungJoon Lee3, and Meng-Sing Liou4 NASA Glenn Research Center, Cleveland, Ohio, 44135 Abstract A hybrid wingbody (HWB) concept is being considered by NASA as a potential subsonic transport aircraft that meets aerodynamic, fuel, emission, and noise goals in the time frame of the 2030s. While the concept promises advantages over conventional wing-and-tube aircraft, it poses unknowns and risks, thus requiring in-depth and broad assessments. Specifically, the configuration entails a tight integration of the airframe and propulsion geometries; the aerodynamic impact has to be carefully evaluated. With the propulsion nacelle installed on the (upper) body, the lift and drag are affected by the mutual interference effects between the airframe and nacelle. The static margin for longitudinal stability is also adversely changed. We develop a design approach in which the integrated geometry of airframe (HWB) and propulsion is accounted for simultaneously in a simple algebraic manner, via parameterization of the planform and airfoils at control sections of the wingbody. In this paper, we present the design of a 300-passenger transport that employs distributed electric fans for propulsion. The trim for stability is achieved through the use of the wingtip twist angle. The geometric shape variables are determined through the adjoint optimization method by minimizing the drag while subject to lift, pitch moment, and geometry constraints. The design results clearly show the influence on the aerodynamic characteristics of the installed nacelle and trimming for stability. A drag minimization with the trim constraint yields a reduction of 10 counts in the drag coefficient. -

UNIT – 4 FORCES on IMMERSED BODIES Lecture-01
1 UNIT – 4 FORCES ON IMMERSED BODIES Lecture-01 Forces on immersed bodies When a body is immersed in a real fluid, which is flowing at a uniform velocity U, the fluid will exert a force on the body. The total force (FR) can be resolved in two components: 1. Drag (FD): Component of the total force in the direction of motion of fluid. 2. Lift (FL): Component of the total force in the perpendicular direction of the motion of fluid. It occurs only when the axis of the body is inclined to the direction of fluid flow. If the axis of the body is parallel to the fluid flow, lift force will be zero. Expression for Drag & Lift Forces acting on the small elemental area dA are: i. Pressure force acting perpendicular to the surface i.e. p dA ii. Shear force acting along the tangential direction to the surface i.e. τ0dA (a) Drag force (FD) : Drag force on elemental area = p dAcosθ + τ0 dAcos(90 – θ = p dAosθ + τ0dAsinθ Hence Total drag (or profile drag) is given by, Where �� = ∫ � cos � �� + ∫�0 sin � �� = pressure drag or form drag, and ∫ � cos � �� = shear drag or friction drag or skin drag (b) Lift0 force (F ) : ∫ � sin � ��L Lift force on the elemental area = − p dAsinθ + τ0 dA sin(90 – θ = − p dAsiθ + τ0dAcosθ Hence, total lift is given by http://www.rgpvonline.com �� = ∫�0 cos � �� − ∫ p sin � �� 2 The drag & lift for a body moving in a fluid of density at a uniform velocity U are calculated mathematically as 2 � And �� = � � � 2 � Where A = projected area of the body or�� largest= � project� � area of the immersed body. -

Introduction to Aerodynamics < 1.7. Dimensional Analysis > Physical
Introduction to Aerodynamics < 1.7. Dimensional analysis > Physical parameters Q: What physical quantities influence forces and moments? V A l Aerodynamics 2015 fall - 1 - Introduction to Aerodynamics < 1.7. Dimensional analysis > Physical parameters Physical quantities to be considered Parameter Symbol units Lift L' MLT-2 Angle of attack α - -1 Freestream velocity V∞ LT -3 Freestream density ρ∞ ML -1 -1 Freestream viscosity μ∞ ML T -1 Freestream speed of sound a∞ LT Size of body (e.g. chord) c L Generally, resultant aerodynamic force: R = f(ρ∞, V∞, c, μ∞, a∞) (1) Aerodynamics 2015 fall - 2 - Introduction to Aerodynamics < 1.7. Dimensional analysis > The Buckingham PI Theorem The relation with N physical variables f1 ( p1 , p2 , p3 , … , pN ) = 0 can be expressed as f 2( P1 , P2 , ... , PN-K ) = 0 where K is the No. of fundamental dimensions Then P1 =f3 ( p1 , p2 , … , pK , pK+1 ) P2 =f4 ( p1 , p2 , … , pK , pK+2 ) …. PN-K =f ( p1 , p2 , … , pK , pN ) Aerodynamics 2015 fall - 3 - < 1.7. Dimensional analysis > The Buckingham PI Theorem Example) Aerodynamics 2015 fall - 4 - < 1.7. Dimensional analysis > The Buckingham PI Theorem Example) Aerodynamics 2015 fall - 5 - < 1.7. Dimensional analysis > The Buckingham PI Theorem Aerodynamics 2015 fall - 6 - < 1.7. Dimensional analysis > The Buckingham PI Theorem Through similar procedure Aerodynamics 2015 fall - 7 - Introduction to Aerodynamics < 1.7. Dimensional analysis > Dimensionless form Aerodynamics 2015 fall - 8 - Introduction to Aerodynamics < 1.8. Flow similarity > Dynamic similarity Two different flows are dynamically similar if • Streamline patterns are similar • Velocity, pressure, temperature distributions are same • Force coefficients are same Criteria • Geometrically similar • Similarity parameters (Re, M) are same Aerodynamics 2015 fall - 9 - Introduction to Aerodynamics < 1.8. -

Aerodynamic Force Measurement on an Icing Airfoil
AerE 344: Undergraduate Aerodynamics and Propulsion Laboratory Lab Instructions Lab #13: Aerodynamic Force Measurement on an Icing Airfoil Instructor: Dr. Hui Hu Department of Aerospace Engineering Iowa State University Office: Room 2251, Howe Hall Tel:515-294-0094 Email:[email protected] Lab #13: Aerodynamic Force Measurement on an Icing Airfoil Objective: The objective of this lab is to measure the aerodynamic forces acting on an airfoil in a wind tunnel using a direct force balance. The forces will be measured on an airfoil before and after the accretion of ice to illustrate the effect of icing on the performance of aerodynamic bodies. The experiment components: The experiments will be performed in the ISU-UTAS Icing Research Tunnel, a closed-circuit refrigerated wind tunnel located in the Aerospace Engineering Department of Iowa State University. The tunnel has a test section with a 16 in 16 in cross section and all the walls of the test section optically transparent. The wind tunnel has a contraction section upstream the test section with a spray system that produces water droplets with the 10–100 um mean droplet diameters and water mass concentrations of 0–10 g/m3. The tunnel is refrigerated by a Vilter 340 system capable of achieving operating air temperatures below -20 C. The freestream velocity of the tunnel can set up to ~50 m/s. Figure 1 shows the calibration information for the tunnel, relating the freestream velocity to the motor frequency setting. Figure 1. Wind tunnel airspeed versus motor frequency setting. The airfoil model for the lab is a finite wing NACA 0012 with a chord length of 6 inches and a span of 14.5 inches.