Upwind Sail Aerodynamics : a RANS Numerical Investigation Validated with Wind Tunnel Pressure Measurements I.M Viola, Patrick Bot, M
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Airfoil Drag by Wake Survey Using Ldv
AIRFOIL DRAG BY WAKE SURVEY USING LDV 1 Purpose This experiment introduces the student to the use of Laser Doppler Velocimetry (LDV) as a means of measuring air flow velocities. The section drag of a NACA 0012 airfoil is determined from velocity measurements obtained in the airfoil wake. 2 Apparatus (1) .5 m x .7 m wind tunnel (max velocity 20 m/s) (2) NACA 0015 airfoil (0.2 m chord, 0.7 m span) (3) Betz manometer (4) Pitot tube (5) DISA LDV optics (6) Spectra Physics 124B 15 mW laser (632.8 nm) (7) DISA 55N20 LDV frequency tracker (8) TSI atomizer using 50cs silicone oil (9) XYZ LDV traversing system (10) Computer data reduction program 1 3 Notation A wing area (m2) b initial laser beam radius (m) bo minimum laser beam radius at lens focus (m) c airfoil chord length (m) Cd drag coefficient da elemental area in wake survey plane (m2) d drag force per unit span f focal length of primary lens (m) fo Doppler frequency (Hz) I detected signal amplitude (V) l distance across survey plane (m) r seed particle radius (m) s airfoil span (m) v seed particle velocity (instantaneous flow velocity) (m/s) U wake velocity (m/s) Uo upstream flow velocity (m/s) α Mie scatter size parameter/angle of attack (degs) δy fringe separation (m) θ intersection angle of laser beams λ laser wavelength (632.8 nm for He Ne laser) ρ air density at NTP (1.225 kg/m3) τ Doppler period (s) 4 Theory 4.1 Introduction The profile drag of a two-dimensional airfoil is the sum of the form drag due to boundary layer sep- aration (pressure drag), and the skin friction drag. -
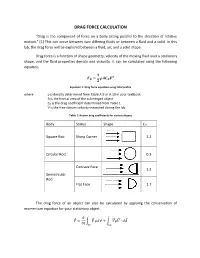
Drag Force Calculation
DRAG FORCE CALCULATION “Drag is the component of force on a body acting parallel to the direction of relative motion.” [1] This can occur between two differing fluids or between a fluid and a solid. In this lab, the drag force will be explored between a fluid, air, and a solid shape. Drag force is a function of shape geometry, velocity of the moving fluid over a stationary shape, and the fluid properties density and viscosity. It can be calculated using the following equation, ퟏ 푭 = 흆푨푪 푽ퟐ 푫 ퟐ 푫 Equation 1: Drag force equation using total profile where ρ is density determined from Table A.9 or A.10 in your textbook A is the frontal area of the submerged object CD is the drag coefficient determined from Table 1 V is the free-stream velocity measured during the lab Table 1: Known drag coefficients for various shapes Body Status Shape CD Square Rod Sharp Corner 2.2 Circular Rod 0.3 Concave Face 1.2 Semicircular Rod Flat Face 1.7 The drag force of an object can also be calculated by applying the conservation of momentum equation for your stationary object. 휕 퐹⃗ = ∫ 푉⃗⃗ 휌푑∀ + ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 휕푡 퐶푉 퐶푆 Assuming steady flow, the equation reduces to 퐹⃗ = ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 퐶푆 The following frontal view of the duct is shown below. Integrating the velocity profile after the shape will allow calculation of drag force per unit span. Figure 1: Velocity profile after an inserted shape. Combining the previous equation with Figure 1, the following equation is obtained: 푊 퐷푓 = ∫ 휌푈푖(푈∞ − 푈푖)퐿푑푦 0 Simplifying the equation, you get: 20 퐷푓 = 휌퐿 ∑ 푈푖(푈∞ − 푈푖)훥푦 푖=1 Equation 2: Drag force equation using wake profile The pressure measurements can be converted into velocity using the Bernoulli’s equation as follows: 2Δ푃푖 푈푖 = √ 휌퐴푖푟 Be sure to remember that the manometers used are in W.C. -

Experimental Analysis of a Low Cost Lift and Drag Force Measurement System for Educational Sessions
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 04 Issue: 09 | Sep -2017 www.irjet.net p-ISSN: 2395-0072 Experimental Analysis of a Low Cost Lift and Drag Force Measurement System for Educational Sessions Asutosh Boro B.Tech National Institute of Technology Srinagar Indian Institute of Science, Bangalore 560012 ---------------------------------------------------------------------***--------------------------------------------------------------------- Abstract - A low cost Lift and Drag force measurement wind- tunnel and used for educational learning with good system was designed, fabricated and tested in wind tunnel accuracy. In addition, an indirect wind tunnel velocity to be used for basic practical lab sessions. It consists of a measurement capability of the designed system was mechanical linkage system, piezo-resistive sensors and tested. NACA airfoil 4209 was chosen as the test subject to NACA Airfoil to test its performance. The system was tested measure its performance and tests were done at various at various velocities and angle of attacks and experimental angles of attack and velocities 11m/s, 12m/s and 14m/s. coefficient of lift and drag were then compared with The force and coefficient results obtained were compared literature values to find the errors. A decent accuracy was with literature data from airfoil tools[1] to find the deduced from the lift data and the considerable error in system’s accuracy. drag was due to concentration of drag forces across a narrow force range and sensor’s fluctuations across that 1.1 Methodology range. It was inferred that drag system will be as accurate as the lift system when the drag forces are large. -

Chapter 4: Immersed Body Flow [Pp
MECH 3492 Fluid Mechanics and Applications Univ. of Manitoba Fall Term, 2017 Chapter 4: Immersed Body Flow [pp. 445-459 (8e), or 374-386 (9e)] Dr. Bing-Chen Wang Dept. of Mechanical Engineering Univ. of Manitoba, Winnipeg, MB, R3T 5V6 When a viscous fluid flow passes a solid body (fully-immersed in the fluid), the body experiences a net force, F, which can be decomposed into two components: a drag force F , which is parallel to the flow direction, and • D a lift force F , which is perpendicular to the flow direction. • L The drag coefficient CD and lift coefficient CL are defined as follows: FD FL CD = 1 2 and CL = 1 2 , (112) 2 ρU A 2 ρU Ap respectively. Here, U is the free-stream velocity, A is the “wetted area” (total surface area in contact with fluid), and Ap is the “planform area” (maximum projected area of an object such as a wing). In the remainder of this section, we focus our attention on the drag forces. As discussed previously, there are two types of drag forces acting on a solid body immersed in a viscous flow: friction drag (also called “viscous drag”), due to the wall friction shear stress exerted on the • surface of a solid body; pressure drag (also called “form drag”), due to the difference in the pressure exerted on the front • and rear surfaces of a solid body. The friction drag and pressure drag on a finite immersed body are defined as FD,vis = τwdA and FD, pres = pdA , (113) ZA ZA Streamwise component respectively. -

Aerodynamics Material - Taylor & Francis
CopyrightAerodynamics material - Taylor & Francis ______________________________________________________________________ 257 Aerodynamics Symbol List Symbol Definition Units a speed of sound ⁄ a speed of sound at sea level ⁄ A area aspect ratio ‐‐‐‐‐‐‐‐ b wing span c chord length c Copyrightmean aerodynamic material chord- Taylor & Francis specific heat at constant pressure of air · root chord tip chord specific heat at constant volume of air · / quarter chord total drag coefficient ‐‐‐‐‐‐‐‐ , induced drag coefficient ‐‐‐‐‐‐‐‐ , parasite drag coefficient ‐‐‐‐‐‐‐‐ , wave drag coefficient ‐‐‐‐‐‐‐‐ local skin friction coefficient ‐‐‐‐‐‐‐‐ lift coefficient ‐‐‐‐‐‐‐‐ , compressible lift coefficient ‐‐‐‐‐‐‐‐ compressible moment ‐‐‐‐‐‐‐‐ , coefficient , pitching moment coefficient ‐‐‐‐‐‐‐‐ , rolling moment coefficient ‐‐‐‐‐‐‐‐ , yawing moment coefficient ‐‐‐‐‐‐‐‐ ______________________________________________________________________ 258 Aerodynamics Aerodynamics Symbol List (cont.) Symbol Definition Units pressure coefficient ‐‐‐‐‐‐‐‐ compressible pressure ‐‐‐‐‐‐‐‐ , coefficient , critical pressure coefficient ‐‐‐‐‐‐‐‐ , supersonic pressure coefficient ‐‐‐‐‐‐‐‐ D total drag induced drag Copyright material - Taylor & Francis parasite drag e span efficiency factor ‐‐‐‐‐‐‐‐ L lift pitching moment · rolling moment · yawing moment · M mach number ‐‐‐‐‐‐‐‐ critical mach number ‐‐‐‐‐‐‐‐ free stream mach number ‐‐‐‐‐‐‐‐ P static pressure ⁄ total pressure ⁄ free stream pressure ⁄ q dynamic pressure ⁄ R -

Enhancing General Aviation Aircraft Safety with Supplemental Angle of Attack Systems
University of North Dakota UND Scholarly Commons Theses and Dissertations Theses, Dissertations, and Senior Projects January 2015 Enhancing General Aviation Aircraft aS fety With Supplemental Angle Of Attack Systems David E. Kugler Follow this and additional works at: https://commons.und.edu/theses Recommended Citation Kugler, David E., "Enhancing General Aviation Aircraft aS fety With Supplemental Angle Of Attack Systems" (2015). Theses and Dissertations. 1793. https://commons.und.edu/theses/1793 This Dissertation is brought to you for free and open access by the Theses, Dissertations, and Senior Projects at UND Scholarly Commons. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of UND Scholarly Commons. For more information, please contact [email protected]. ENHANCING GENERAL AVIATION AIRCRAFT SAFETY WITH SUPPLEMENTAL ANGLE OF ATTACK SYSTEMS by David E. Kugler Bachelor of Science, United States Air Force Academy, 1983 Master of Arts, University of North Dakota, 1991 Master of Science, University of North Dakota, 2011 A Dissertation Submitted to the Graduate Faculty of the University of North Dakota in partial fulfillment of the requirements for the degree of Doctor of Philosophy Grand Forks, North Dakota May 2015 Copyright 2015 David E. Kugler ii PERMISSION Title Enhancing General Aviation Aircraft Safety With Supplemental Angle of Attack Systems Department Aviation Degree Doctor of Philosophy In presenting this dissertation in partial fulfillment of the requirements for a graduate degree from the University of North Dakota, I agree that the library of this University shall make it freely available for inspection. I further agree that permission for extensive copying for scholarly purposes may be granted by the professor who supervised my dissertation work or, in his absence, by the Chairperson of the department or the dean of the School of Graduate Studies. -

Numerical Optimization and Wind-Tunnel Testing of Low
Numerical Optimization and WindTunnel Testing of Low ReynoldsNumber Airfoils y Th Lutz W Wurz and S Wagner University of Stuttgart D Stuttgart Germany Abstract A numerical optimization to ol has been applied to the design of low Reynolds number airfoils Re The aero dynamic mo del is based on the Eppler co de with ma jor extensions A new robust mo del for the calculation of short n transitional separation bubbles was implemented along with an e transition criterion and Drelas turbulent b oundarylayer pro cedure with a mo died shap efactor relation The metho d was coupled with a commercial hybrid optimizer and applied to p erform unconstrained high degree of freedom optimizations with ob jective to minimize the drag for a sp ecied lift range One resulting airfoil was tested in the Mo del WindTunnel MWT of the institute and compared to the classical RG airfoil In order to allow a realistic recalculation of exp eriments conducted in the MWT the limiting nfactor was evaluated for this facility A sp ecial airfoil featuring an extensive instability zone was designed for this purp ose The investigation was supplemented by detailed measurements of the turbulence level Toget more insight in design guidelines for very low Reynolds numb er airfoils the inuence of variations of the leadingedge geometry on the aero dynamic characteristics was studied exp erimentally at Re Intro duction For the Reynoldsnumber regime of aircraft wingsections Re sophisticated di rect and inverse metho ds for airfoil analysis and design are available -

Sailing for Performance
SD2706 Sailing for Performance Objective: Learn to calculate the performance of sailing boats Today: Sailplan aerodynamics Recap User input: Rig dimensions ‣ P,E,J,I,LPG,BAD Hull offset file Lines Processing Program, LPP: ‣ Example.bri LPP_for_VPP.m rigdata Hydrostatic calculations Loading condition ‣ GZdata,V,LOA,BMAX,KG,LCB, hulldata ‣ WK,LCG LCF,AWP,BWL,TC,CM,D,CP,LW, T,LCBfpp,LCFfpp Keel geometry ‣ TK,C Solve equilibrium State variables: Environmental variables: solve_Netwon.m iterative ‣ VS,HEEL ‣ TWS,TWA ‣ 2-dim Netwon-Raphson iterative method Hydrodynamics Aerodynamics calc_hydro.m calc_aero.m VS,HEEL dF,dM Canoe body viscous drag Lift ‣ RFC ‣ CL Residuals Viscous drag Residuary drag calc_residuals_Newton.m ‣ RR + dRRH ‣ CD ‣ dF = FAX + FHX (FORCE) Keel fin drag ‣ dM = MH + MR (MOMENT) Induced drag ‣ RF ‣ CDi Centre of effort Centre of effort ‣ CEH ‣ CEA FH,CEH FA,CEA The rig As we see it Sail plan ≈ Mainsail + Jib (or genoa) + Spinnaker The sail plan is defined by: IMSYC-66 P Mainsail hoist [m] P E Boom leech length [m] BAD Boom above deck [m] I I Height of fore triangle [m] J Base of fore triangle [m] LPG Perpendicular of jib [m] CEA CEA Centre of effort [m] R Reef factor [-] J E LPG BAD D Sailplan modelling What is the purpose of the sails on our yacht? To maximize boat speed on a given course in a given wind strength ‣ Max driving force, within our available righting moment Since: We seek: Fx (Thrust vs Resistance) ‣ Driving force, FAx Fy (Side forces, Sails vs. Keel) ‣ Heeling force, FAy (Mx (Heeling-righting moment)) ‣ Heeling arm, CAE Aerodynamics of sails A sail is: ‣ a foil with very small thickness and large camber, ‣ with flexible geometry, ‣ usually operating together with another sail ‣ and operating at a large variety of angles of attack ‣ Environment L D V Each vertical section is a differently cambered thin foil Aerodynamics of sails TWIST due to e.g. -

How Do Wings Generate Lift? 2
GENERAL ARTICLE How Do Wings Generate Lift? 2. Myths, Approximate Theories and Why They All Work M D Deshpande and M Sivapragasam A cambered surface that is moving forward in a fluid gen- erates lift. To explain this interesting fact in terms of sim- pler models, some preparatory concepts were discussed in the first part of this article. We also agreed on what is an accept- able explanation. Then some popular models were discussed. Some quantitative theories will be discussed in this conclud- ing part. Finally we will tie up all these ideas together and connect them to the rigorous momentum theorem. M D Deshpande is a Professor in the Faculty of Engineering The triumphant vindication of bold theories – are these not the and Technology at M S Ramaiah University of pride and justification of our life’s work? Applied Sciences. Sherlock Holmes, The Valley of Fear Sir Arthur Conan Doyle 1. Introduction M Sivapragasam is an We start here with two quantitative theories before going to the Assistant Professor in the momentum conservation principle in the next section. Faculty of Engineering and Technology at M S Ramaiah University of Applied 1.1 The Thin Airfoil Theory Sciences. This elegant approximate theory takes us further than what was discussed in the last two sections of Part 111, and quantifies the Resonance, Vol.22, No.1, ideas to get expressions for lift and moment that are remarkably pp.61–77, 2017. accurate. The pressure distribution on the airfoil, apart from cre- ating a lift force, leads to a nose-up or nose-down moment also. -

Technology for Pressure-Instrumented Thin Airfoil Models
NASA-CR-3891 19850015493 NASA Contractor Report 3891 i 1 Technology for Pressure-Instrumented Thin Airfoil Models David A. Wigley ., ..... " .... _' /, !..... .,L_. '' CONTRACT NAS1-17571 MAY 1985 ( • " " c _J ._._l._,.. ¸_ - j, ;_.. , r_ '._:i , _ . ; . ,. NIA NASA Contractor Report 3891 Technology for Pressure-Instrumented Thin Airfoil Models David A. Wigley Applied Cryogenics & Materials Consultants, Inc. New Castle, Delaware Prepared for Langley Research Center under Contract NAS1-17571 N//X National Aeronautics and Space Administration Scientific and Technical InformationBranch 1985 Use of trademarks or names of manufacturers in this report does not constitute an official endorsement of such products or manufacturers, either expressed or implied, by the National Aeronautics and Space Administration. FINAL REPORT ON PHASE 1 OF NASA CONTRACT NASI-17571 "TECHNOLOGY FOR PRESSURE-INSTRUMENTED THIN AIRFOIL MODELS" PROJECT SU_IARY The objective of Phase 1 of this research was to identify, then select and evaluate, the most appropriate combination of materials and fabrication techniques required to produce a Pressure Instrumented Thin Airfoil model for testing in a Cryogenic wind Tunnel ( PITACT ). Particular attention was to be given to proving the feasability and reliability of each sub-stage and ensuring that they could be combined together without compromising the quality of the resultant segment or model. In order to provide a sharp focus for this research, experimental samples were to be fabricated as if they were trailing edge segments of a 6% thick supercritical airfoil, number 0631X7, scaled to a 325mm (13in.) chord, the maximum likely to be tested in the 13in. x 13in. adaptive wall test section of the 0.3m Transonic Cryogenic Tunnel at NASA Langley Research Center. -

Aerodynamic Characteristics of Naca 0012 Airfoil Section at Different Angles of Attack
AERODYNAMIC CHARACTERISTICS OF NACA 0012 AIRFOIL SECTION AT DIFFERENT ANGLES OF ATTACK SUPREETH NARASIMHAMURTHY GRADUATE STUDENT 1327291 Table of Contents 1) Introduction………………………………………………………………………………………………………………………………………...1 2) Methodology……………………………………………………………………………………………………………………………………….3 3) Results……………………………………………………………………………………………………………………………………………......5 4) Conclusion …………………………………………………………………………………………………………………………………………..9 5) References…………………………………………………………………………………………………………………………………………10 List of Figures Figure 1: Basic nomenclature of an airfoil………………………………………………………………………………………………...1 Figure 2: Computational domain………………………………………………………………………………………………………………4 Figure 3: Static Pressure Contours for different angles of attack……………………………………………………………..5 Figure 4: Velocity Magnitude Contours for different angles of attack………………………………………………………………………7 Fig 5: Variation of Cl and Cd with alpha……………………………………………………………………………………………………8 Figure 6: Lift Coefficient and Drag Coefficient Ratio for Re = 50000…………………………………………………………8 List of Tables Table 1: Lift and Drag coefficients as calculated from lift and drag forces from formulae given above……7 Introduction It is a fact of common experience that a body in motion through a fluid experience a resultant force which, in most cases is mainly a resistance to the motion. A class of body exists, However for which the component of the resultant force normal to the direction to the motion is many time greater than the component resisting the motion, and the possibility of the flight of an airplane depends on the use of the body of this class for wing structure. Airfoil is such an aerodynamic shape that when it moves through air, the air is split and passes above and below the wing. The wing’s upper surface is shaped so the air rushing over the top speeds up and stretches out. This decreases the air pressure above the wing. The air flowing below the wing moves in a comparatively straighter line, so its speed and air pressure remain the same. -

CHAPTER TWO - Static Aeroelasticity – Unswept Wing Structural Loads and Performance 21 2.1 Background
Static aeroelasticity – structural loads and performance CHAPTER TWO - Static Aeroelasticity – Unswept wing structural loads and performance 21 2.1 Background ........................................................................................................................... 21 2.1.2 Scope and purpose ....................................................................................................................... 21 2.1.2 The structures enterprise and its relation to aeroelasticity ............................................................ 22 2.1.3 The evolution of aircraft wing structures-form follows function ................................................ 24 2.2 Analytical modeling............................................................................................................... 30 2.2.1 The typical section, the flying door and Rayleigh-Ritz idealizations ................................................ 31 2.2.2 – Functional diagrams and operators – modeling the aeroelastic feedback process ....................... 33 2.3 Matrix structural analysis – stiffness matrices and strain energy .......................................... 34 2.4 An example - Construction of a structural stiffness matrix – the shear center concept ........ 38 2.5 Subsonic aerodynamics - fundamentals ................................................................................ 40 2.5.1 Reference points – the center of pressure..................................................................................... 44 2.5.2 A different