ME 1404 Fluid Mechanics Drag and Lift
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Glossary Physics (I-Introduction)
1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay. -

Airfoil Drag by Wake Survey Using Ldv
AIRFOIL DRAG BY WAKE SURVEY USING LDV 1 Purpose This experiment introduces the student to the use of Laser Doppler Velocimetry (LDV) as a means of measuring air flow velocities. The section drag of a NACA 0012 airfoil is determined from velocity measurements obtained in the airfoil wake. 2 Apparatus (1) .5 m x .7 m wind tunnel (max velocity 20 m/s) (2) NACA 0015 airfoil (0.2 m chord, 0.7 m span) (3) Betz manometer (4) Pitot tube (5) DISA LDV optics (6) Spectra Physics 124B 15 mW laser (632.8 nm) (7) DISA 55N20 LDV frequency tracker (8) TSI atomizer using 50cs silicone oil (9) XYZ LDV traversing system (10) Computer data reduction program 1 3 Notation A wing area (m2) b initial laser beam radius (m) bo minimum laser beam radius at lens focus (m) c airfoil chord length (m) Cd drag coefficient da elemental area in wake survey plane (m2) d drag force per unit span f focal length of primary lens (m) fo Doppler frequency (Hz) I detected signal amplitude (V) l distance across survey plane (m) r seed particle radius (m) s airfoil span (m) v seed particle velocity (instantaneous flow velocity) (m/s) U wake velocity (m/s) Uo upstream flow velocity (m/s) α Mie scatter size parameter/angle of attack (degs) δy fringe separation (m) θ intersection angle of laser beams λ laser wavelength (632.8 nm for He Ne laser) ρ air density at NTP (1.225 kg/m3) τ Doppler period (s) 4 Theory 4.1 Introduction The profile drag of a two-dimensional airfoil is the sum of the form drag due to boundary layer sep- aration (pressure drag), and the skin friction drag. -
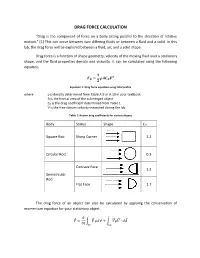
Drag Force Calculation
DRAG FORCE CALCULATION “Drag is the component of force on a body acting parallel to the direction of relative motion.” [1] This can occur between two differing fluids or between a fluid and a solid. In this lab, the drag force will be explored between a fluid, air, and a solid shape. Drag force is a function of shape geometry, velocity of the moving fluid over a stationary shape, and the fluid properties density and viscosity. It can be calculated using the following equation, ퟏ 푭 = 흆푨푪 푽ퟐ 푫 ퟐ 푫 Equation 1: Drag force equation using total profile where ρ is density determined from Table A.9 or A.10 in your textbook A is the frontal area of the submerged object CD is the drag coefficient determined from Table 1 V is the free-stream velocity measured during the lab Table 1: Known drag coefficients for various shapes Body Status Shape CD Square Rod Sharp Corner 2.2 Circular Rod 0.3 Concave Face 1.2 Semicircular Rod Flat Face 1.7 The drag force of an object can also be calculated by applying the conservation of momentum equation for your stationary object. 휕 퐹⃗ = ∫ 푉⃗⃗ 휌푑∀ + ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 휕푡 퐶푉 퐶푆 Assuming steady flow, the equation reduces to 퐹⃗ = ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 퐶푆 The following frontal view of the duct is shown below. Integrating the velocity profile after the shape will allow calculation of drag force per unit span. Figure 1: Velocity profile after an inserted shape. Combining the previous equation with Figure 1, the following equation is obtained: 푊 퐷푓 = ∫ 휌푈푖(푈∞ − 푈푖)퐿푑푦 0 Simplifying the equation, you get: 20 퐷푓 = 휌퐿 ∑ 푈푖(푈∞ − 푈푖)훥푦 푖=1 Equation 2: Drag force equation using wake profile The pressure measurements can be converted into velocity using the Bernoulli’s equation as follows: 2Δ푃푖 푈푖 = √ 휌퐴푖푟 Be sure to remember that the manometers used are in W.C. -

Experimental Analysis of a Low Cost Lift and Drag Force Measurement System for Educational Sessions
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 04 Issue: 09 | Sep -2017 www.irjet.net p-ISSN: 2395-0072 Experimental Analysis of a Low Cost Lift and Drag Force Measurement System for Educational Sessions Asutosh Boro B.Tech National Institute of Technology Srinagar Indian Institute of Science, Bangalore 560012 ---------------------------------------------------------------------***--------------------------------------------------------------------- Abstract - A low cost Lift and Drag force measurement wind- tunnel and used for educational learning with good system was designed, fabricated and tested in wind tunnel accuracy. In addition, an indirect wind tunnel velocity to be used for basic practical lab sessions. It consists of a measurement capability of the designed system was mechanical linkage system, piezo-resistive sensors and tested. NACA airfoil 4209 was chosen as the test subject to NACA Airfoil to test its performance. The system was tested measure its performance and tests were done at various at various velocities and angle of attacks and experimental angles of attack and velocities 11m/s, 12m/s and 14m/s. coefficient of lift and drag were then compared with The force and coefficient results obtained were compared literature values to find the errors. A decent accuracy was with literature data from airfoil tools[1] to find the deduced from the lift data and the considerable error in system’s accuracy. drag was due to concentration of drag forces across a narrow force range and sensor’s fluctuations across that 1.1 Methodology range. It was inferred that drag system will be as accurate as the lift system when the drag forces are large. -

Chapter 4: Immersed Body Flow [Pp
MECH 3492 Fluid Mechanics and Applications Univ. of Manitoba Fall Term, 2017 Chapter 4: Immersed Body Flow [pp. 445-459 (8e), or 374-386 (9e)] Dr. Bing-Chen Wang Dept. of Mechanical Engineering Univ. of Manitoba, Winnipeg, MB, R3T 5V6 When a viscous fluid flow passes a solid body (fully-immersed in the fluid), the body experiences a net force, F, which can be decomposed into two components: a drag force F , which is parallel to the flow direction, and • D a lift force F , which is perpendicular to the flow direction. • L The drag coefficient CD and lift coefficient CL are defined as follows: FD FL CD = 1 2 and CL = 1 2 , (112) 2 ρU A 2 ρU Ap respectively. Here, U is the free-stream velocity, A is the “wetted area” (total surface area in contact with fluid), and Ap is the “planform area” (maximum projected area of an object such as a wing). In the remainder of this section, we focus our attention on the drag forces. As discussed previously, there are two types of drag forces acting on a solid body immersed in a viscous flow: friction drag (also called “viscous drag”), due to the wall friction shear stress exerted on the • surface of a solid body; pressure drag (also called “form drag”), due to the difference in the pressure exerted on the front • and rear surfaces of a solid body. The friction drag and pressure drag on a finite immersed body are defined as FD,vis = τwdA and FD, pres = pdA , (113) ZA ZA Streamwise component respectively. -

Drag Coefficients of Inclined Hollow Cylinders
Drag Coefficients of Inclined Hollow Cylinders: RANS versus LES A Major Qualifying Project Report Submitted to the Faculty of the WORCESTER POLYTECHNIC INSTITUTE in partial fulfillment of the requirements for the Degree of Bachelor of Science In Chemical Engineering By Ben Franzluebbers _______________ Date: April 2013 Approved: ________________________ Dr. Anthony G. Dixon, Advisor Abstract The goal of this project was use LES and RANS (SST k-ω) CFD turbulence models to find the drag coefficient of a hollow cylinder at various inclinations and compare the results. The drag coefficients were evaluated for three angles relative to the flow (0⁰, 45⁰, and 90⁰) and three Reynolds numbers (1000, 5000, and 10000). The drag coefficients determined by LES and RANS agreed for the 0⁰ and 90⁰ inclined hollow cylinder. For the 45⁰ inclined hollow cylinder the RANS model predicted drag coefficients about 0.2 lower the drag coefficients predicted by LES. 2 Executive Summary The design of catalyst particles is an important topic in the chemical industry. Chemical products made using catalytic processes are worth $900 billion a year and about 75% of all chemical and petroleum products by value (U.S. Climate Change Technology Program, 2005). The catalyst particles used for fixed bed reactors are an important part of this. Knowing properties of the catalyst particle such as the drag coefficient is necessary to understand how fluid flow will be affected by the packed bed. The particles are inclined at different angles in the reactor and can come in a wide variety of shapes meaning that understanding the effect of particle shape on drag coefficient has practical importance. -

On the Generation of a Reverse Von Kármán Street for the Controlled Cylinder Wake in the Laminar Regime
On the generation of a reverse Von Kármán street for the controlled cylinder wake in the laminar regime Michel Bergmann,∗ Laurent Cordier, and Jean-Pierre Brancher LEMTA, UMR 7563 (CNRS - INPL - UHP) ENSEM - 2, avenue de la forêt de Haye BP 160 - 54504 Vandœuvre cedex, France (Dated: December 8, 2005) 1 Abstract In this Brief Communication we are interested in the maximum mean drag reduction that can be achieved under rotary sinusoidal control for the circular cylinder wake in the laminar regime. For a Reynolds number equal to 200, we give numerical evidence that partial control restricted to an upstream part of the cylinder surface may increase considerably the effectiveness of the control. Indeed, a maximum value of relative mean drag reduction equal to 30% is obtained when applying a specific sinusoidal control to the whole cylinder, where up to 75% of reduction can be obtained when the same control law is applied only to a well selected upstream part of the cylinder. This result suggests that a mean flow correction field with negative drag is observable for this controlled flow configuration. The significant thrust force that is locally generated in the near wake corresponds to a reverse Kármán vortex street as commonly observed in fish-like locomotion or flapping wing flight. Finally, the energetic efficiency of the control is quantified by examining the Power Saving Ratio: it is shown that our approach is energetically inefficient. However, it is also demonstrated that for this control scheme the improvement of the effectiveness goes generally with an improvement of the efficiency. Keywords: Partial rotary control ; Cylinder wake ; Drag minimization ; reverse Kármán vortex street. -

Sailing for Performance
SD2706 Sailing for Performance Objective: Learn to calculate the performance of sailing boats Today: Sailplan aerodynamics Recap User input: Rig dimensions ‣ P,E,J,I,LPG,BAD Hull offset file Lines Processing Program, LPP: ‣ Example.bri LPP_for_VPP.m rigdata Hydrostatic calculations Loading condition ‣ GZdata,V,LOA,BMAX,KG,LCB, hulldata ‣ WK,LCG LCF,AWP,BWL,TC,CM,D,CP,LW, T,LCBfpp,LCFfpp Keel geometry ‣ TK,C Solve equilibrium State variables: Environmental variables: solve_Netwon.m iterative ‣ VS,HEEL ‣ TWS,TWA ‣ 2-dim Netwon-Raphson iterative method Hydrodynamics Aerodynamics calc_hydro.m calc_aero.m VS,HEEL dF,dM Canoe body viscous drag Lift ‣ RFC ‣ CL Residuals Viscous drag Residuary drag calc_residuals_Newton.m ‣ RR + dRRH ‣ CD ‣ dF = FAX + FHX (FORCE) Keel fin drag ‣ dM = MH + MR (MOMENT) Induced drag ‣ RF ‣ CDi Centre of effort Centre of effort ‣ CEH ‣ CEA FH,CEH FA,CEA The rig As we see it Sail plan ≈ Mainsail + Jib (or genoa) + Spinnaker The sail plan is defined by: IMSYC-66 P Mainsail hoist [m] P E Boom leech length [m] BAD Boom above deck [m] I I Height of fore triangle [m] J Base of fore triangle [m] LPG Perpendicular of jib [m] CEA CEA Centre of effort [m] R Reef factor [-] J E LPG BAD D Sailplan modelling What is the purpose of the sails on our yacht? To maximize boat speed on a given course in a given wind strength ‣ Max driving force, within our available righting moment Since: We seek: Fx (Thrust vs Resistance) ‣ Driving force, FAx Fy (Side forces, Sails vs. Keel) ‣ Heeling force, FAy (Mx (Heeling-righting moment)) ‣ Heeling arm, CAE Aerodynamics of sails A sail is: ‣ a foil with very small thickness and large camber, ‣ with flexible geometry, ‣ usually operating together with another sail ‣ and operating at a large variety of angles of attack ‣ Environment L D V Each vertical section is a differently cambered thin foil Aerodynamics of sails TWIST due to e.g. -

How Do Wings Generate Lift? 2
GENERAL ARTICLE How Do Wings Generate Lift? 2. Myths, Approximate Theories and Why They All Work M D Deshpande and M Sivapragasam A cambered surface that is moving forward in a fluid gen- erates lift. To explain this interesting fact in terms of sim- pler models, some preparatory concepts were discussed in the first part of this article. We also agreed on what is an accept- able explanation. Then some popular models were discussed. Some quantitative theories will be discussed in this conclud- ing part. Finally we will tie up all these ideas together and connect them to the rigorous momentum theorem. M D Deshpande is a Professor in the Faculty of Engineering The triumphant vindication of bold theories – are these not the and Technology at M S Ramaiah University of pride and justification of our life’s work? Applied Sciences. Sherlock Holmes, The Valley of Fear Sir Arthur Conan Doyle 1. Introduction M Sivapragasam is an We start here with two quantitative theories before going to the Assistant Professor in the momentum conservation principle in the next section. Faculty of Engineering and Technology at M S Ramaiah University of Applied 1.1 The Thin Airfoil Theory Sciences. This elegant approximate theory takes us further than what was discussed in the last two sections of Part 111, and quantifies the Resonance, Vol.22, No.1, ideas to get expressions for lift and moment that are remarkably pp.61–77, 2017. accurate. The pressure distribution on the airfoil, apart from cre- ating a lift force, leads to a nose-up or nose-down moment also. -

Aerodynamics of High-Performance Wing Sails
Aerodynamics of High-Performance Wing Sails J. otto Scherer^ Some of tfie primary requirements for tiie design of wing sails are discussed. In particular, ttie requirements for maximizing thrust when sailing to windward and tacking downwind are presented. The results of water channel tests on six sail section shapes are also presented. These test results Include the data for the double-slotted flapped wing sail designed by David Hubbard for A. F. Dl Mauro's lYRU "C" class catamaran Patient Lady II. Introduction The propulsion system is probably the single most neglect ed area of yacht design. The conventional triangular "soft" sails, while simple, practical, and traditional, are a long way from being aerodynamically desirable. The aerodynamic driving force of the sails is, of course, just as large and just as important as the hydrodynamic resistance of the hull. Yet, designers will go to great lengths to fair hull lines and tank test hull shapes, while simply drawing a triangle on the plans to define the sails. There is no question in my mind that the application of the wealth of available airfoil technology will yield enormous gains in yacht performance when applied to sail design. Re cent years have seen the application of some of this technolo gy in the form of wing sails on the lYRU "C" class catamar ans. In this paper, I will review some of the aerodynamic re quirements of yacht sails which have led to the development of the wing sails. For purposes of discussion, we can divide sail require ments into three points of sailing: • Upwind and close reaching. -

A Concept of the Vortex Lift of Sharp-Edge Delta Wings Based on a Leading-Edge-Suction Analogy Tech Library Kafb, Nm
I A CONCEPT OF THE VORTEX LIFT OF SHARP-EDGE DELTA WINGS BASED ON A LEADING-EDGE-SUCTION ANALOGY TECH LIBRARY KAFB, NM OL3042b NASA TN D-3767 A CONCEPT OF THE VORTEX LIFT OF SHARP-EDGE DELTA WINGS BASED ON A LEADING-EDGE-SUCTION ANALOGY By Edward C. Polhamus Langley Research Center Langley Station, Hampton, Va. NATIONAL AERONAUTICS AND SPACE ADMINISTRATION For sale by the Clearinghouse for Federal Scientific and Technical Information Springfield, Virginia 22151 - Price $1.00 A CONCEPT OF THE VORTEX LIFT OF SHARP-EDGE DELTA WINGS BASED ON A LEADING-EDGE-SUCTION ANALOGY By Edward C. Polhamus Langley Research Center SUMMARY A concept for the calculation of the vortex lift of sharp-edge delta wings is pre sented and compared with experimental data. The concept is based on an analogy between the vortex lift and the leading-edge suction associated with the potential flow about the leading edge. This concept, when combined with potential-flow theory modified to include the nonlinearities associated with the exact boundary condition and the loss of the lift component of the leading-edge suction, provides excellent prediction of the total lift for a wide range of delta wings up to angles of attack of 20° or greater. INTRODUCTION The aerodynamic characteristics of thin sharp-edge delta wings are of interest for supersonic aircraft and have been the subject of theoretical and experimental studies for many years in both the subsonic and supersonic speed ranges. Of particular interest at subsonic speeds has been the formation and influence of the leading-edge separation vor tex that occurs on wings having sharp, highly swept leading edges. -

Formula 1 Race Car Performance Improvement by Optimization of the Aerodynamic Relationship Between the Front and Rear Wings
The Pennsylvania State University The Graduate School College of Engineering FORMULA 1 RACE CAR PERFORMANCE IMPROVEMENT BY OPTIMIZATION OF THE AERODYNAMIC RELATIONSHIP BETWEEN THE FRONT AND REAR WINGS A Thesis in Aerospace Engineering by Unmukt Rajeev Bhatnagar © 2014 Unmukt Rajeev Bhatnagar Submitted in Partial Fulfillment of the Requirements for the Degree of Master of Science December 2014 The thesis of Unmukt R. Bhatnagar was reviewed and approved* by the following: Mark D. Maughmer Professor of Aerospace Engineering Thesis Adviser Sven Schmitz Assistant Professor of Aerospace Engineering George A. Lesieutre Professor of Aerospace Engineering Head of the Department of Aerospace Engineering *Signatures are on file in the Graduate School ii Abstract The sport of Formula 1 (F1) has been a proving ground for race fanatics and engineers for more than half a century. With every driver wanting to go faster and beat the previous best time, research and innovation in engineering of the car is really essential. Although higher speeds are the main criterion for determining the Formula 1 car’s aerodynamic setup, post the San Marino Grand Prix of 1994, the engineering research and development has also targeted for driver’s safety. The governing body of Formula 1, i.e. Fédération Internationale de l'Automobile (FIA) has made significant rule changes since this time, primarily targeting car safety and speed. Aerodynamic performance of a F1 car is currently one of the vital aspects of performance gain, as marginal gains are obtained due to engine and mechanical changes to the car. Thus, it has become the key to success in this sport, resulting in teams spending millions of dollars on research and development in this sector each year.