PHOTODISSOCIATION DYNAMICS of GROUP V HYDRIDES By
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Hazardous Material Inventory Statement
City of Brooklyn Park FIRE DEPARTMENT 5200 - 85th Avenue North Brooklyn Park MN 55443 Phone: (763)493-8020 Fax: (763) 493-8391 Hazardous Materials Inventory Statement Users Guide A separate inventory statement shall be provided for each building. An amended inventory statement shall be provided within 30 days of the storage of any hazardous materials or plastics that changes or adds a hazard class or which is sufficient in quantity to cause an increase in the quantity which exceeds 5 percent for any hazard class. The hazardous materials inventory statement shall list by hazard class categories. Each grouping shall provide the following information for each hazardous material listed for that group including a total quantity for each group of hazard class. 1. Hazard class. (See attached Hazardous Materials Categories Listing) 2. Common or trade name. 3. Chemical Abstract Service Number (CAS number) found in 29 Code of Federal Regulations (C.F.R.). 4. Whether the material is pure or a mixture, and whether the material is a solid, liquid or gas 5. Maximum aggregate quantity stored at any one time. 6. Maximum aggregate quantity In-Use (Open to atmosphere) at any one time. 7. Maximum aggregate quantity In-Use (Closed to atmosphere) at any one time. 8. Storage conditions related to the storage type, high-pile, encapsulated, non-encapsulated. Attached is a listing of categories that all materials need to be organized to. Definitions of these categories are also attached for your use. At the end of this packet are blank forms for completing this project. For questions regarding Hazardous Materials Inventory Statement contact the Fire Department at 763-493-8020. -

Search for New Three-, Four-Component Petasis, Passerini
J. Chem. Chem. Eng. 8 (2014) 428-432 D DAVID PUBLISHING Search for New Three-, Four-Component Petasis, Passerini, Hantzsch, Kabachnic-Fields, Ugi Reactions with Organic Compounds of Phosphorus, Arsenic, Antimony and Bismuth Aibassov Erkin Zhakenovich*, Yemelyanova Valentina Stepanovna, Shakieva Tatyana Vladimirovna, Tussupbaev Nessipbay Kuandykovich and Blagikh Evgeniy Vladimirovich Research Institute of New Chemical Technologies and Materials, Kazakh National University Al-Farabi, Almaty 005012, Kazakhstan Received: November 29, 2013 / Accepted: December 18, 2013 / Published: April 25, 2014. Abstract: It is discovered a new three-, four-component Petasis, Passerini, Hantzsch, Kabachnic-Fields, Ugi reactions with of arsine, stibine and bismuthine in organometallic chemistry. Modifications were replaced to a nitrogen atom of classical reactions of atoms of phosphorus, arsenic, antimony and bismuth. It has been proposed a new mechanism for possible reactions. Key words: Petasis, Passerini, Hantzsch, Kabachnic-Fields, Ugi reactions, phosphorus, arsenic, antimony, bismuth. 1. Introduction four-component reactions Petasis, Passerini, Hantzsch, Kabachnic-Fields, Ugi reactions with organic In recent years, it has been actively investigated compounds of phosphorus, arsenic, antimony and nucleophilic reaction organilgalogenidami phosphine bismuth. and with electrophilic geterilalkenami allowing to obtain primary, secondary and tertiary phosphines, 2. Theory selectively and with high yield. Most of these It is known that the Petasis reaction is a MCR reactions are realized under mild conditions at a (multi component reaction) that enables the pressure atmlosfernom phosphine. preparation of amines and their derivatives such as Although the chemistry of organophosphorus α-amino acids. compounds devoted a considerable number of monographs, but the reaction of organic compounds of arsenic, antimony and bismuth are very limited. -

2019 Minnesota Chemicals of High Concern List
Minnesota Department of Health, Chemicals of High Concern List, 2019 Persistent, Bioaccumulative, Toxic (PBT) or very Persistent, very High Production CAS Bioaccumulative Use Example(s) and/or Volume (HPV) Number Chemical Name Health Endpoint(s) (vPvB) Source(s) Chemical Class Chemical1 Maine (CA Prop 65; IARC; IRIS; NTP Wood and textiles finishes, Cancer, Respiratory 11th ROC); WA Appen1; WA CHCC; disinfection, tissue 50-00-0 Formaldehyde x system, Eye irritant Minnesota HRV; Minnesota RAA preservative Gastrointestinal Minnesota HRL Contaminant 50-00-0 Formaldehyde (in water) system EU Category 1 Endocrine disruptor pesticide 50-29-3 DDT, technical, p,p'DDT Endocrine system Maine (CA Prop 65; IARC; IRIS; NTP PAH (chem-class) 11th ROC; OSPAR Chemicals of Concern; EuC Endocrine Disruptor Cancer, Endocrine Priority List; EPA Final PBT Rule for 50-32-8 Benzo(a)pyrene x x system TRI; EPA Priority PBT); Oregon P3 List; WA Appen1; Minnesota HRV WA Appen1; Minnesota HRL Dyes and diaminophenol mfg, wood preservation, 51-28-5 2,4-Dinitrophenol Eyes pesticide, pharmaceutical Maine (CA Prop 65; IARC; NTP 11th Preparation of amino resins, 51-79-6 Urethane (Ethyl carbamate) Cancer, Development ROC); WA Appen1 solubilizer, chemical intermediate Maine (CA Prop 65; IARC; IRIS; NTP Research; PAH (chem-class) 11th ROC; EPA Final PBT Rule for 53-70-3 Dibenzo(a,h)anthracene Cancer x TRI; WA PBT List; OSPAR Chemicals of Concern); WA Appen1; Oregon P3 List Maine (CA Prop 65; NTP 11th ROC); Research 53-96-3 2-Acetylaminofluorene Cancer WA Appen1 Maine (CA Prop 65; IARC; IRIS; NTP Lubricant, antioxidant, 55-18-5 N-Nitrosodiethylamine Cancer 11th ROC); WA Appen1 plastics stabilizer Maine (CA Prop 65; IRIS; NTP 11th Pesticide (EPA reg. -

Structural Evidence for Pnictogen-Centered Lewis Acidity in Cationic Platinum-Stibine Complexes Featuring Pendent Amino Or Ammonium Groups †
molecules Article Structural Evidence for Pnictogen-Centered Lewis Acidity in Cationic Platinum-Stibine Complexes Featuring Pendent Amino or Ammonium Groups † Roberta R. Rodrigues and François P. Gabbaï * Department of Chemistry, Texas A&M University, College Station, TX 77843-3255, USA; [email protected] * Correspondence: [email protected]; Tel.: +1-979-862-2070 † In memory of Alan H. Cowley, a most inspiring Ph.D. advisor, and a great friend. Abstract: As part of our continuing interest in the chemistry of cationic antimony Lewis acids as ligands for late transition metals, we have now investigated the synthesis of platinum complexes featuring a triarylstibine ligand substituted by an o-[(dimethylamino)methyl]phenyl group referred N N to as Ar . More specifically, we describe the synthesis of the amino stibine ligand Ph2SbAr (L) and its platinum dichloride complex [LPtCl]Cl which exists as a chloride salt and which shows weak coordination of the amino group to the antimony center. We also report the conversion of [LPtCl]Cl 3+ into a tricationic complex [LHPt(SMe2)] which has been isolated as a tris-triflate salt after reaction of [LPtCl]Cl with SMe2, HOTf and AgOTf. Finally, we show that [LHPt(SMe2)][OTf]3 acts as a catalyst for the cyclization of 2-allyl-2-(2-propynyl)malonate. Citation: Rodrigues, R.R.; Gabbaï, Keywords: pnictogen bonding; platinum; catalysis F.P. Structural Evidence for Pnictogen-Centered Lewis Acidity in Cationic Platinum-Stibine Complexes Featuring Pendent Amino or 1. Introduction Ammonium Groups . Molecules 2021, The chemistry of stibines is attracted a renewed interest because of applications in 26, 1985. -
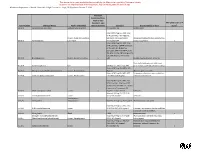
Sorted by CAS Number
This document is made available electronically by the Minnesota Legislative Reference Library as part of an ongoing digital archiving project. http://www.leg.state.mn.us/lrl/lrl.asp Minnesota Department of Health, Chemicals of High Concern list, July 1, 2010 (updated October 7, 2010) Persistent, Bioaccumulative, Toxic or very Persistent, very HPV (2006 and 3 of 4 CAS Number Chemical Name Health endpoint(s) Bioaccumulative Source(s) Use example(s) or class years)1 50-00-0 Formaldehyde (in water) Gastrointestinal system Minnesota HRL Contaminant Maine (CA Prop 65; IARC; IRIS; NTP 11th ROC); WA Appen1; Cancer, Respiratory system, WA CHCC; Minnesota HRV; Wood and textiles finishes, disinfection, 50-00-0 Formaldehyde Eye irritant Minnesota RAA tissue preservative x Maine (CA Prop 65; IARC; IRIS; NTP 11th ROC; OSPAR Chemicals of Concern; EU Endocrine Disruptor; EPA Final PBT Rule for TRI; EPA Priority PBT); Oregon P3 List; WA Appen1; Minnesota 50-32-8 Benzo(a)pyrene Cancer, Endocrine system x HRV Combustion by product, research Dyes and diaminophenol mfg, wood 51-28-5 2,4-Dinitrophenol Eyes WA Appen1; Minnesota HRL preservation, pesticide, pharmaceutical Maine (CA Prop 65; IARC); WA 51-75-2 Nitrogen mustard (Mechlorethamine) Cancer, Development Appen1 Warfare agent, research Maine (CA Prop 65; IARC; NTP Preparation of amino resins, solubilizer, 51-79-6 Urethane (Ethyl carbamate) Cancer, Development 11th ROC); WA Appen1 chemical intermediate Maine (CA Prop 65; IARC; IRIS; NTP 11th ROC; EPA Final PBT Rule for TRI; WA PBT List; OSPAR Chemicals -

Coordination Chemistry of the Main Group Elements with Phosphine, Arsine and Stibine Ligands
Coordination Chemistry Reviews 260 (2014) 65–115 Contents lists available at ScienceDirect Coordination Chemistry Reviews jo urnal homepage: www.elsevier.com/locate/ccr Review Coordination chemistry of the main group elements with phosphine, arsine and stibine ligands ∗ Jennifer Burt, William Levason , Gillian Reid School of Chemistry, University of Southampton, Southampton SO17 1BJ, UK Contents 1. Introduction . 66 2. Bonding . 66 3. Characterisation techniques . 67 4. s-Block complexes . 68 5. Group 12 . 68 5.1. Zinc . 69 5.2. Cadmium . 70 5.3. Mercury . 71 6. Group 13 . 74 6.1. Boron . 74 6.2. Aluminium. 76 6.3. Gallium . 81 6.4. Indium . 87 6.5. Thallium . 93 7. Group 14 . 94 7.1. Silicon. 94 7.2. Germanium . 94 7.3. Tin . 98 7.4. Lead . 102 8. Group 15 . 102 8.1. Phosphorus . 103 8.2. Arsenic . 103 8.3. Antimony . 104 8.4. Bismuth . 106 9. Group 16 . 108 10. Applications and outlook . .. -

Chemical Inventory Packet / Calarp Lists / HFD / Dmg 2004 Table 1
HAYWARD FIRE DEPARTMENT CHEMICAL INVENTORY WORKSHEET To prepare a chemical inventory based on the Hayward Fire Code, you are required to report the quantities of chemicals found in the facility, separated by Hazard Category, and by location. You are also to classify the chemicals as to storage and manner of use. Handling and storage requirements are determined by these factors: the nature of the chemical or its hazard; the location; the manner of use or storage; and the quantity involved in each particular manner of use or storage. A Control Area is a building, a portion of the building, or an outside area where chemicals are allowed to be stored, dispensed, used or handled subject to certain conditions and requirements. This packet consists of the following lists and the Chemical Inventory Worksheet form: 1. Hazardous Materials Hazard Categories. This is the list printed on goldenrod paper. Based on the Uniform Fire Code, this is the classification of chemicals by hazard categories. The different hazard categories are defined and examples are provided for each. Most chemicals exhibit more than one hazard, and all hazards should be considered when preparing your chemical inventory. 2. Tables of Regulated Substances Under the CalARP Program. Printed on pink paper, these are the lists of flammable and toxic substances that, if present at or above certain threshold quantities, will require the preparation of a Risk Management Plan 3. Federal List of Extremely Hazardous Substances (EHS). This list is printed on blue paper. These are the substances that the federal government classifies as extremely hazardous substances. The Hayward Fire Department has included “CalARP-Listed or EHS-Listed Chemicals” as a separate Hazard Category. -

GLOSSARY of CLASS NAMES of ORGANIC COMPOUNDS and REACTIVE INTERMEDIATES BASED on STRUCTURE (IUPAC Recommendations 1995)
Pure &App/. Chem., Vol. 67, Nos 819, pp. 1307-1375, 1995. Printed in Great Britain. (B 1995 IUPAC INTERNATIONAL UNION OF PURE AND APPLIED CHEMISTRY ORGANIC CHEMISTRY DMSION COMMISSION ON NOMENCLATURE OF ORGANIC CHEMISTRY (III. 1) COMMISSION ON PHYSICAL ORGANIC CHEMISTRY (III.2) GLOSSARY OF CLASS NAMES OF ORGANIC COMPOUNDS AND REACTIVE INTERMEDIATES BASED ON STRUCTURE (IUPAC Recommendations 1995) Prepared for publication by G.P. MOSS, P.A.S. SMITH and D. TAVERNIER Cornpodtion of the ZZZ.1 & 111.2 Working Party (1980-1994): H.J.T. Bos, A.J. Boulton, E.W. Godly, P. Griinanger, A.D. McNaught, G.P. Moss, R. PanicO, J. Rigaudy, P.A.S. Smith (Conwnorfiom ZZZ, I), J.H. Stocker, D. Tavernier, R.A.Y. Jones, J. March, J.M. McBnde, P. Miiller (Conwnorfim 111.2). Membership of the Commission on Nomenclature of Organic Chemistry during the preparation of this document (1980-1994) was as follows: Titular Members: 0. Achmatowicz (Poland) 1979-1987; H. J. T. Bos (Netherlands) 1987- , Vice-Chairman, 1991- ; J. R. Bull (Republic of South Africa) 1987-1993; H. A. Favre (Canada) 1989- , Chairman, 1991- ; P. M. Giles, Jr. (USA) 1989- ; E. W. Godly (UK) 1987-1993. Secretary, 1989-1993 ; D. Hellwinkel (Federal Republic of Germany) 1979-1987, Vice- Chairman, 1981-1987; B. J. Herold (Portugal) 1994- ; K. Hirayama (Japan) 1975-1983; M. V. KisakUrck (Switizrland) 1994- ; A. D. McNaught (UK) 1979-1987; G. P. Moss (UK) 1977- 1987, Chairinan, 1981- 1987, Vice-Chainnun, 1979-1981; R. Panico (Francc) 1981-1991, Vice- Chairman, 1989-1991; W. H. Powell (USA) Secretary, 1979-1989; J. -
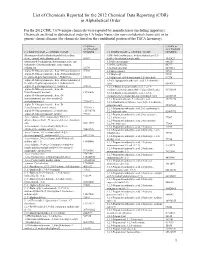
List of Chemicals Reported for the 2012 Chemical Data Reporting (CDR) in Alphabetical Order
List of Chemicals Reported for the 2012 Chemical Data Reporting (CDR) in Alphabetical Order For the 2012 CDR, 7,674 unique chemicals were reported by manufacturers (including importers). Chemicals are listed in alphabetical order by CA Index Name (for non-confidential chemicals) or by generic chemical name (for chemicals listed on the confidential portion of the TSCA Inventory). CASRN or CASRN or ACCESSION ACCESSION CA INDEX NAME or GENERIC NAME NUMBER CA INDEX NAME or GENERIC NAME NUMBER (Benzoquinolinyl)-(alkylimidazolyl)indenedione 1(3H)-Isobenzofuranone, 6-(dimethylamino)-3,3- deriv., compd. with alkanoic acid 56907 bis[4-( dimethylamino)phenyl]- 1552427 (Substituted-5-sulfophenyl heteromonocycle) azo- 1,10-Decanediamine 646253 (substituted 2-hydroxyphenyl), iron complex, 1,10-Phenanthroline 66717 sodium salt 20736 1,12-Dodecanediol 5675514 .alpha.-D-Glucopyranoside, .beta.-D-fructofuranosyl 57501 1,1'-Bicyclohexyl 92513 .alpha.-D-Glucopyranoside, .beta.-D-fructofuranosyl 1,1'-Biphenyl 92524 O-.alpha.-D-galactopyranosyl-( 1.fwdarw.6)- 512696 1,1'-Biphenyl, 4,4'-diisocyanato-3,3'-dimethyl- 91974 .alpha.-D-Glucopyranoside, .beta.-D-fructofuranosyl 1,1-Cyclopropanedicarboxylic acid, 1,1-dimethyl O-.alpha.-D-galactopyranosyl-( 1.fwdarw.6)-O- ester 6914712 .alpha.-D-g alactopyranosyl-(1.fwdarw.6)- 470553 1,2,3,4-Butanetetracarboxylic acid, 1,2,3,4- .alpha.-D-Glucopyranoside, .beta.-D- tetrakis(1,2,2,6,6-pentamethyl-4 -piperidinyl) ester 91788839 fructofuranosyl, benzoate 12738646 1,2,3,4-Butanetetracarboxylic acid, 1,2,3,4- .alpha.-D-Glucopyranoside, -

Coordination Chemistry of the Main Group Elements with Phosphine
Coordination Chemistry Reviews 260 (2014) 65–115 Contents lists available at ScienceDirect Coordination Chemistry Reviews jo urnal homepage: www.elsevier.com/locate/ccr Review Coordination chemistry of the main group elements with phosphine, arsine and stibine ligands ∗ Jennifer Burt, William Levason , Gillian Reid School of Chemistry, University of Southampton, Southampton SO17 1BJ, UK Contents 1. Introduction . 66 2. Bonding . 66 3. Characterisation techniques . 67 4. s-Block complexes . 68 5. Group 12 . 68 5.1. Zinc . 69 5.2. Cadmium . 70 5.3. Mercury . 71 6. Group 13 . 74 6.1. Boron . 74 6.2. Aluminium. 76 6.3. Gallium . 81 6.4. Indium . 87 6.5. Thallium . 93 7. Group 14 . 94 7.1. Silicon. 94 7.2. Germanium . 94 7.3. Tin . 98 7.4. Lead . 102 8. Group 15 . 102 8.1. Phosphorus . 103 8.2. Arsenic . 103 8.3. Antimony . 104 8.4. Bismuth . 106 9. Group 16 . 108 10. Applications and outlook . .. -
PREFACE This Volume of the Sotubitity Data Series Covers The
PREFACE This volume of The Sotubitity Data Series covers the solubility of ammonia, N-methy1methanamine and N,N-dimethy1methanamine in pure liquids not including water. Data on the solubility of some higher amines at pressures below the vapor pressure of the liquid amine are also included as are data on the solubility of deuterated methanamine and deuterated N-methy1methanamine. The volume also covers the avail able data on the solubility of phosphine, arsine, stibine, bismuthine, silane, germane ~nd stannane in non-aqueous solvents. The editors believe that all solubility values published up to June 1983 have been included but would be grateful to learn of significant omissions. In few cases can one be certain that the available data has an accuracy better than about ±3%. In many cases data may have an accuracy less than this. It is hoped that this and other similar volumes in The SoZubiZity Data Series will draw attention to the systems for which there is lack of good data and will stimulate further experimental work in the field. The editors wish to make a plea that authors pUblishing gas solubility data should always report the primary experimental observa tions of temperature, pressure, volume, etc. and should indicate the precise method used to calculate solubility values. Much of the value, for instance, of an Ostwald coefficient is lost if the pressure at which measurements were made is not reported. Henry's law constants have been defined and calculated in a variety of ways and the precise significance of a particular value is ofton lost if pressure measurements are not given. -

Nomenclature of Organic Chemistry. IUPAC Recommendations and Preferred Names 2013. Prepared for Publication by Henri A
International Union of Pure and Applied Chemistry Division VIII Chemical Nomenclature and Structure Representation Division Nomenclature of Organic Chemistry. IUPAC Recommendations and Preferred Names 2013. Prepared for publication by Henri A. Favre and Warren H. Powell, Royal Society of Chemistry, ISBN 978-0-85404-182-4 Chapter P-5 SELECTING PREFERRED IUPAC NAMES AND CONSTRUCTING NAMES OF ORGANIC COMPOUNDS P-50 Introduction P-51 Selecting the preferred type of IUPAC nomenclature P-52 Selecting preferred IUPAC names and preselected names for parent hydrides P-53 Selecting preferred retained names of parent hydrides P-54 Selecting the preferred method for modifying the degree of hydrogenation P-55 Selecting the preferred retained name for functional parent compounds P-56 Selecting the preferred suffix for the principal characteristic groups P-57 Selecting preferred and preselected prefixes for substituent group names P-58 Selection of preferred IUPAC names P-59 Name construction P-50 INTRODUCTION Many compounds can have two or more names in accordance with several methods recommended by IUPAC for their formation, one of which is recommended herein as the preferred IUPAC name (PIN). This Chapter summarizes the selection rules that are recommended in Chapters P-1 through P-4 for generation of preferred IUPAC names for compounds described in these Chapters and also in Chapters P-6 to P-10 where applicable. Substitutive nomenclature is the principal type of nomenclature for organic compounds; however, other types are recommended because substitutive nomenclature was never recommended for naming certain classes of compounds or because they represent a simplification when the substitutive names become long and cumbersome.