Dollo's Law and the Re-Evolution of Shell Coiling
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

E Urban Sanctuary Algae and Marine Invertebrates of Ricketts Point Marine Sanctuary
!e Urban Sanctuary Algae and Marine Invertebrates of Ricketts Point Marine Sanctuary Jessica Reeves & John Buckeridge Published by: Greypath Productions Marine Care Ricketts Point PO Box 7356, Beaumaris 3193 Copyright © 2012 Marine Care Ricketts Point !is work is copyright. Apart from any use permitted under the Copyright Act 1968, no part may be reproduced by any process without prior written permission of the publisher. Photographs remain copyright of the individual photographers listed. ISBN 978-0-9804483-5-1 Designed and typeset by Anthony Bright Edited by Alison Vaughan Printed by Hawker Brownlow Education Cheltenham, Victoria Cover photo: Rocky reef habitat at Ricketts Point Marine Sanctuary, David Reinhard Contents Introduction v Visiting the Sanctuary vii How to use this book viii Warning viii Habitat ix Depth x Distribution x Abundance xi Reference xi A note on nomenclature xii Acknowledgements xii Species descriptions 1 Algal key 116 Marine invertebrate key 116 Glossary 118 Further reading 120 Index 122 iii Figure 1: Ricketts Point Marine Sanctuary. !e intertidal zone rocky shore platform dominated by the brown alga Hormosira banksii. Photograph: John Buckeridge. iv Introduction Most Australians live near the sea – it is part of our national psyche. We exercise in it, explore it, relax by it, "sh in it – some even paint it – but most of us simply enjoy its changing modes and its fascinating beauty. Ricketts Point Marine Sanctuary comprises 115 hectares of protected marine environment, located o# Beaumaris in Melbourne’s southeast ("gs 1–2). !e sanctuary includes the coastal waters from Table Rock Point to Quiet Corner, from the high tide mark to approximately 400 metres o#shore. -
(1943: 724, Pi. 71, Fig. 16) Illustration of Calyptraea (Deeper Into the Aperture) on the Right/Posterior
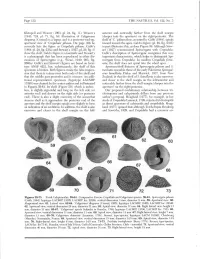
Page 118 THE NAUTILUS, Vol. 122, No. 3 Kleinpeil and Weaver (1963, pi. 24, fig. 11). Weavers anterior and noticeably farther from the shell margin (1943: 724, pi. 71, fig. 16) illustration of Calyptraea (deeper into the aperture) on the right/posterior. The diegoana (Conrad) is a lapsus and is a posterior-end-up, shelf of 'C.y pileum thus, as noted by Gabb (1864), spirals apertural view of 'Crepidula' pileum. On page 356 he inward toward the apex. Gabb's figure (pi. 29, fig. 233b) correctly lists the figure as Crepidula pileum. Gabb's in part illustrates this, as does Figure 59. Although Stew- (1864: pi. 29, fig. 233a) and Stewart's (1927, pi. 29, fig. 3) art (1927) synonomized Spirocrypta with Crepidula, show the shelf. Gabb's figure is a fascimile and Stewart's Gabb's description of Spirocrypta recognizes this very is a photograph that has been reproduced in other dis- important characteristic, which helps to distinguish Spi- cussions of Spirocrypta (e.g., Wenz, 1940: 903, fig. rocrypta from Crepidula. In modern Crepidula forni- 2660a). Gabb's and Stewart's figures are based on lecto- cata, the shelf does not spiral into the whorl apex. type ANSP 4221, but, unfortunately, the shelf of this Aperture/shelf features of Spirocrypta pileum and S. specimen is broken. Both figures create the false impres- inomata resemble those of the early Paleocene Spirogal- sion that there is a sinus near both ends of the shelf and erus lamellaria Finlay and Marwick, 1937, from New that the middle part protrudes and is concave. -

Port of Lyttleton Baseline Survey for Non-Indigenous Marine Species
Port of Lyttelton Baseline survey for non-indigenous marine species (Research Project ZBS2000/04) Biosecurity New Zealand Technical Paper No: 2005/01 Prepared for BNZ Post-clearance Directorate by Graeme Inglis, Nick Gust, Isla Fitridge, Oliver Floerl, Chris Woods, Barbara Hayden, Graham Fenwick ISBN No: 0-478-07922-2 ISSN No: 1176-838X March 2006 Disclaimer While every effort has been made to ensure the information in this publication is accurate, the Ministry of Agriculture and Forestry does not accept any responsibility or liability for error or fact omission, interpretation or opinion which may be present, nor for the consequences of any decisions based on this information. Any view or opinions expressed do not necessarily represent the official view of the Ministry of Agriculture and Forestry. The information in this report and any accompanying documentation is accurate to the best of the knowledge and belief of the National Institute of Water & Atmospheric Research Ltd (NIWA) acting on behalf of the Ministry of Agriculture and Forestry. While NIWA has exercised all reasonable skill and care in preparation of information in this report, neither NIWA nor the Ministry of Agriculture and Forestry accept any liability in contract, tort or otherwise for any loss, damage, injury, or expense, whether direct, indirect or consequential, arising out of the provision of information in this report. Requests for further copies should be directed to: Publication Adviser MAF Information Bureau P O Box 2526 WELLINGTON Telephone: (04) 474 4100 Facsimile: -

Cretaceous Trichotropid Gastropods from the Pacific Slope of North America: Possible Pathways to Calyptraeid Morphology
THE NAUTILUS 122(3):115–142, 2008 Page 115 Cretaceous trichotropid gastropods from the Pacific slope of North America: Possible pathways to calyptraeid morphology LouElla R. Saul Richard L. Squires Invertebrate Paleontology Section Department of Geological Sciences Natural History Museum of California State University, Los Angeles County Northridge, CA 91330-8266 USA 900 Exposition Boulevard, [email protected] Los Angeles, CA 90007 USA [email protected] ABSTRACT tropods which has received little or no study regarding its ancestry, point of origin in terms of time and geographic Late Cretaceous gastropods belonging to genus Lysis Gabb, 1864, from the Pacific slope of North America, bridge the mor- locale, and evolutionary history. Specimens have been phologic gap between turbiniform trichotropids and limpet-like found in shallow-marine Cretaceous deposits from calyptraeids. Development of the depressed and broadened southern Vancouver Island and neighboring Gulf Is- inner lip/columella of Lysis resulted in a larger aperture that lands, British Columbia, Canada to northern Baja Cali- allowed more space for the foot to grasp a hard substrate. fornia, Mexico (Figure 1) and, although Lysis-like gas- Pacific slope species of Lysis are represented by five species tropods have been reported at a few locales in the world, that collectively span an interval from late Coniacian to late its familial placement has been uncertain. This study Maastrichtian. They stem from two lineages of the trichotro- brings new information about all of these items. pine genus Ariadnaria Habe, 1961. The first lineage, which Material for this study included type specimens, addi- includes Ariadnaria ainikta new species of late Albian to Cen- tional collections from their type localities, and speci- omanian age, Ariadnaria stibara new species of Cenomanian age, and Ariadnaria obstricta (White, 1889) of late Coniacian? mens of Late Cretaceous age (Coniacian to Maastrich- and Santonian age, gave rise to the Lysis duplicosta group of tian) from previously unreported-upon localities. -

Mimiwhangata Species Lists Meleagris Gallopavo (Wild Turkey) Phasianus Colchicus (Pheasant) 1973 - 2004, R.V
Mimiwhangata Species Lists Meleagris gallopavo (wild turkey) Phasianus colchicus (pheasant) 1973 - 2004, R.V. Grace & V.C. PLOCEIDAE Kerr Passer domesticus domesticus (house sparrow) RALLIDAE Porphyrio porphyrio melanotus (pukeko) Colour Code for entries STURNIDAE Mimiwhangata Marine Report 1973 Acridotheres tristis(myna) Mimiwhangata Ecological Report 1973 Sturnus vulgaris vulgaris (starling) Marine Report 1976-7 ZOSTEROPIDAE Marine Report 1978 Zosterops lateralis lateralis (waxeye) Environmental Impact Report 1982 Marine Report 1984 Coastal Fish survey 2002 ARDEIDAE Ardea novaehollandiae novaehollandiae (white-faced heron) BIRDS Egretta sacra sacra (blue heron) CHARADRIIDAE Bush Charadrius obscurus (New Zealand dotterel) APTERYGIDAE HAEMATOPODIDAE Apteryx australis (brown kiwi) Haematopus unicolor (variable oystercatcher) COLUMBIDAE LARIDAE Hemiphaga novaeseelandiae (kereru, native Larus novaehollandiae scopulinus (red-billed gull) pigeon) Larus dominicanus (black-backed gull) CUCULIDAE PHALACROCORACIDAE Chrysococcyx lucidus lucidus (shining cuckoo) Phalacrocorax varius (pied shag) MELIPHAGIDAE Phalacrocorax carbo (black shag) Prosthemadera novaeseelandiae (tui) RECURVIROSTRIDAE Anthornis melanura (bellbird) Himantopus himantopus leucocephalus (pied stilt) MUSCICAPIDAE SPHENISCIDAE Gerygone igata (grey warbler) Eudyptula minor (little blue penguin) Rhipidura fuliginosa (fantail) STERNIDAE PLATYCERCIDAE Sterna striata (white fronted tern) Platycercus eximius (eastern rosella) Hydroprogne caspia (caspian tern) STRIGIDAE Ninox novaeseelandiae -

Whangarei Port and Marsden Point) Baseline Survey for Non-Indigenous Marine Species (Research Project ZBS 2000/04)
Whangarei Harbour (Whangarei Port and Marsden Point) Baseline survey for non-indigenous marine species (Research Project ZBS 2000/04) Biosecurity New Zealand Technical Paper No: 2005/16 Prepared for BNZ Post-clearance Directorate by Graeme Inglis, Nick Gust, Isla Fitridge, Oliver Floerl, Chris Woods, Barbara Hayden, Graham Fenwick ISBN No: 0-478-07932-X ISSN No: 1176-838X March 2006 Disclaimer While every effort has been made to ensure the information in this publication is accurate, the Ministry of Agriculture and Forestry does not accept any responsibility or liability for error or fact omission, interpretation or opinion which may be present, nor for the consequences of any decisions based on this information. Any view or opinions expressed do not necessarily represent the official view of the Ministry of Agriculture and Forestry. The information in this report and any accompanying documentation is accurate to the best of the knowledge and belief of the National Institute of Water & Atmospheric Research Ltd (NIWA) acting on behalf of the Ministry of Agriculture and Forestry. While NIWA has exercised all reasonable skill and care in preparation of information in this report, neither NIWA nor the Ministry of Agriculture and Forestry accept any liability in contract, tort or otherwise for any loss, damage, injury, or expense, whether direct, indirect or consequential, arising out of the provision of information in this report. Requests for further copies should be directed to: Publication Adviser MAF Information Bureau P O Box 2526 WELLINGTON -
Marine Ecology
Marsden Point Refinery: A Resource Consent Application to Renew 20 Resource Consents from the Northland Regional Council Prepared for: ChanceryGreen on behalf of The New Zealand Refining Company Limited, trading as ‘Refining NZ’ Prepared by: Gavin Kemble, Director Bridgette Munro, Chairperson Blair McLean, Senior Planner George Sariak, Planner Date Finalised: July 2020 Volume 3f: Marine Ecology Assessment of Effects on Marine Ecological Values Reconsenting of discharges and structures in the CMA Prepared for Refining New Zealand Document Quality Assurance Bibliographic reference for citation: Boffa Miskell Limited 2020. Assessment of Effects on Marine Ecological Values: Reconsenting of discharges and structures in the CMA. Report prepared by Boffa Miskell Limited for Refining New Zealand. Prepared by: Dr Sharon De Luca Associate Partner / Senior Ecologist Boffa Miskell Limited Prepared by: Dr Phillip Ross Marine Ecologist REC Science Status: FINAL Revision / version: E Issue date: 8 July 2020 Use and Reliance This report has been prepared by Boffa Miskell Limited on the specific instructions of our Client. It is solely for our Client’s use for the purpose for which it is intended in accordance with the agreed scope of work. Boffa Miskell does not accept any liability or responsibility in relation to the use of this report contrary to the above, or to any person other than the Client. Any use or reliance by a third party is at that party's own risk. Where information has been supplied by the Client or obtained from other external sources, it has been assumed that it is accurate, without independent verification, unless otherwise indicated. No liability or responsibility is accepted by Boffa Miskell Limited for any errors or omissions to the extent that they arise from inaccurate information provided by the Client or any external source. -

Palaeogene Macrofossils from CRP-3 Drillhole, Victoria Land Basin, Antarctica
Palaeogene Macrofossils from CRP-3 Drillhole, Victoria Land Basin, Antarctica Istituto cli Gcologia Marina. Consiglio Na~ionale(Idle Ricerche. via Gobclli 101. 1-40129 Bologna - Italy ~nstitutcof Geological & Nuclear Sciences. P.O. Box 30 308. Lower Hutt - New Zealand Received 5 March 200 1 : accf,p/ec/ in rcri.sed form 3 July 2001 Abstract - CRP-3 cored Palaeogene strata to 823 metres below the sea floor (mbsf). before passing through Devonian bedrock (Beacon Siipcrgroup) to a depth of 939 mbsf. Palaeogene body fossils have been identified at 239 horizons in the core. The best preserved macrofossils from the core help elucidate the taxonomy. chronology and biogeography of Cenozoic ecosystems of Antarctica. although poor preservation prevents identification to species level in most cases. The lithostratigraphic unit (LSU) of the core top (LSU I. I) contains an almost inonospecific modiolid assemblage, similar to mussel beds recovered in the bottom part of the CRP-212A core. These semi-infauna1 mussels appear to be conspecific, apparently indicating the same age (Early Oligocene) and environment, i.e., a deep muddy shelf characterized by high turbidity and dysoxiclanoxic bottom conditions (high H,S sediment content). LSU 1.2 contains reasonably diverse assemblages representing innerlmiddle shelf environments dominated by epifa~inal suspension feeders. LSU 2.1 contains low-diversity assemblages of suspension feeders (bivalves. brachiopods and bryzoans), probably indicating innerlmiddle shelf environments. LSU 3.1 contains assemblages including infaunal and epifaunal suspension feeders (bivalves, including a scallop, ?Ada/71;(ssiumn.sp.. and solitary corals) and infaunal deposit-feeders, possibly indicating deposition on a deep muddy shelf. -

A Reference List of the Marine Mollusca of New South Wales
AUSTRALIAN MUSEUM SCIENTIFIC PUBLICATIONS Iredale, T., and D. F. McMichael, 1962. A reference list of the marine Mollusca of New South Wales. Australian Museum Memoir 11: 1–109. [30 May 1962]. doi:10.3853/j.0067-1967.11.1962.426 ISSN 0067-1967 Published by the Australian Museum, Sydney naturenature cultureculture discover discover AustralianAustralian Museum Museum science science is is freely freely accessible accessible online online at at www.australianmuseum.net.au/publications/www.australianmuseum.net.au/publications/ 66 CollegeCollege Street,Street, SydneySydney NSWNSW 2010,2010, AustraliaAustralia THE AUSTRALIAN MUSEUM, SYDNEY MEMOIR XI A REFERENCE LIST OF THE MARINE MOLLUSCA OF NEW SOUTH WALES By TOM IREDALE* AND D. F. McMICHAELt * Honorary Zoologist, Australian Museum, Sydney t Curator of Molluscs, Australian Museum, Sydney Published by order of the Trustees J. W. Evans, Se.D. Sydney, May 30, 1962 Registered in Australia for transmission by post as a book PRINTED IN AUSTRALIA BY HALSTEAD PRESS, SYDNEY A REFERENCE LIST OF THE MARINE MOLLUSCA OF NEW SOUTH WALES by TOM lREDALE* AND D. F. McMICHAELt * Honorary Zoologist, Australian Museum, Sydney. t Curator of Molluscs, Australian Museum, Sydney. IN a yQung and prQgressive CGUntry like Australia, T.T. TautO'type, O'r Type Species by TautO'nymy where knGwledge Qf the fauna is increasing rapidly, (Dr by the use Df the specific names typicus O'r it becGmes necessary at least Qnce in each generatiGn typus). to' review prO'gress in systematics with reference lists, L.T. LDgDtype, O'r Type Species by Subsequent which serve as a basis fQr future wQrk. It is nQW DesignatiDn. -

Worldwide Patterns in Mode of Development in Calyptraeid Gastropods
MARINE ECOLOGY PROGRESS SERIES Vol. 247: 103–122, 2003 Published February 4 Mar Ecol Prog Ser Worldwide patterns in mode of development in calyptraeid gastropods Rachel Collin1, 2, 3,* 1Committee on Evolutionary Biology, University of Chicago, Culver Hall, Room 402, 1025 E. 57th Street, Chicago, Illinois 60637, USA 2Department of Zoology, The Field Museum, 1400 South Lake Shore Drive, Chicago, Illinois 60605, USA 3Present address: Smithsonian Tropical Research Institute, Unit 0948, APO AA 34002, USA ABSTRACT: The mode of development in marine invertebrates is believed to have consequences for dispersal, gene flow, geographic range, and speciation and extinction rates. The factors responsible for among-species differences in mode of development are not well understood and patterns of vari- ation in mode of development have not been documented for many groups. I present a compiled data set of developmental characters for 78 species of calyptraeid gastropods: 53 Crepidula, 9 Calyptraea, 11 Crucibulum and 5 other species. Analysis of this data set shows that egg- and hatching-size distri- butions are strongly positively skewed. As expected, egg size correlates with hatching size and time to hatching in species without nurse eggs. Egg size is not significantly different between species with planktotrophic development and species with direct development with nurse eggs. Hatching size of direct developers with and without nurse eggs do not differ. Developmental characters do not vary with adult body size among species. There are strong latitudinal effects in mode of development, the frequency of planktotrophic species decreases with increasing latitude while the proportion of direct developers increases. There is also a striking latitudinal pattern in the occurrence of nurse eggs; almost all species with nurse eggs occur in the southern hemisphere. -

Faunal Changes in Waitemata Harbour Sediments, 1930S‐1990S
See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/233450658 Faunal changes in Waitemata Harbour sediments, 1930s‐1990s Article in Journal- Royal Society of New Zealand · March 1997 DOI: 10.1080/03014223.1997.9517525 CITATIONS READS 32 24 5 authors, including: Bruce W Hayward Margaret S. Morley Geomarine Research Auckland Museum 690 PUBLICATIONS 4,966 CITATIONS 58 PUBLICATIONS 407 CITATIONS SEE PROFILE SEE PROFILE Some of the authors of this publication are also working on these related projects: MSc research - Pleistocene extinctions of deep-sea benthic foraminifera: the South Atlantic record View project Fossil organic-walled microphytoplankton ("acrticarchs" and green algae) View project All content following this page was uploaded by Bruce W Hayward on 07 February 2014. The user has requested enhancement of the downloaded file. © Journal of The Royal Society of New Zealand, Volume 27, Number 1, March 1997, pp 1-20 Faunal changes in Waitemata Harbour sediments, 1930s— 1990s Bruce W. Hayward*, A. Brett Stephenson*, Margaret Morley*, Jenny L. Riley*, Hugh R. Grenfell* A resurvey of Powell's classic study of subtidal, soft-bottom communities in the Waitemata Harbour, Auckland, was undertaken to determine the nature of faunal changes between the 1930s and 1990s. Samples were dredged and associations were intuitively deduced largely on the basis of molluscs and echinoderms, in a similar fashion to Powell's 1930s study. Away from the wharves and marinas the soft-bottom fauna is still remarkably rich and diverse, and retains a similar gross pattern to the 1930s. Fourteen mollusc species (dominantly carnivorous gastropods) appear to have disappeared or suffered major reductions in abundance within the harbour. -

Webversionjubbook2.Pdf
that moves on the ground English version Edited by: Stichting Schepsel Schelp www.fossilshells.nl Printed by:: Pumbo, Zwaag (N.H.) www.pumbo.nl Copyright: Stichting Schepsel Schelp 2016 © All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, digital, electronic, mechanical, photocopying or otherwise, without the prior permission of the publisher. STICHTING SCHEPSEL SCHELP (Foundation Creature Shell From 1991 to 2016 Part 2 The Creator be thanked. Recent Mollusca: POLYPLACOPHORA, CEPHALOPODA 1 Eudoxochiton nobilis Gray, 1843 Chaetopleura peruviana (Lamarck,1829) Takapura Reef, Auckland Region, New Zealand Bahia San Vicente, Chile Colno 31629, 80 mm. Colno 52055, 49 mm. CEPHALOPODA Nautilus pompileus Linnaeus,1758 Nautilus scrobiculatus Lightfoot,1786 Indo Pacific Papua New Guinea, Indonesia Colno 1991, 140 mm. Colno 6163, 160 mm. Spirula spirula Linnaeus,1758 Sepia species Corralejo, Fuerteventura, Canary Islands, Spain Mission Beach, Queensland, Australia Colno 14968, 19 mm. Colno 55582, 78 mm. Argonauta argo Linnaeus,1758 Argonauta boettgeri Maltzan,1881 Western Australia, Australia Durban, KwaZulu-Natal, RSA Colno 34398, 200 mm. Colno 1986, 47 mm. Jubilee book 25 years Stichting Schepsel Schelp Page 5 CEPHALOPODA 2, DENTALIIDA, PATELLOIDEA 1 Argonauta nodosa Lightfoot,1786 Dentalium aprinum Linnaeus,1767 Albany, Western Australia, Australia Philippines Colno 37732, 150 mm. Colno 4694, 90 mm. PATELLOIDEA Dentalium vernedei Sowerby,1860 Patella compressa Linnaeus,1758 Taiwan Olifantsbaai, Western Cape, RSA Colno 20138, 122 mm. Colno 42147, 101 mm. Patella laticostata Blainville,1825 Patella miniata sanguinans Reeve,1856 Albany, I Western Australia, Australia North Transkei, RSA Colno 46712, 91 mm.