DOCSLIB.ORG

1B Paper 6: Communications Pulse Amplitude Modulation (Recap)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
1B Paper 6: Communications Pulse Amplitude Modulation (Recap) 1B Paper 6: Communications Handout 5: Digital Passband Modulation Ramji Venkataramanan Signal Processing and Communications Lab Department of Engineering [email protected] Lent Term 2016 1 / 22 Pulse Amplitude Modulation (recap) Recall that the PAM signal carrying the information symbols X1, X2,... is x (t) = X p(t kT ) b k − ∑k x (t) is a baseband signal • b (Recall: its bandwidth is the same as that of the pulse p(t)) If the channel is a baseband channel, e.g., ethernet cable, we • can directly transmit xb(t) But most channels are passband — we are only allowed to transmit our signal over a fixed frequency band centred around a carrier frequency fc . E.g., a wireless channel may have fc = 2 GHz and channel bandwidth = 10 MHz How do you “up-convert” the PAM signal to passband ? 2 / 22 Baseband to Passband The natural thing to do is to modulate the amplitude of a high-frequency carrier with xb(t): x(t) = xb(t) cos(2πfc t) = Xk p(t kT ) cos(2πfc t) [ − ] ∑k x(t) y(t) n(t) For lack of a standard name, we’ll call this passband • modulation scheme up-converted PAM. Note the similarity with analogue modulation (DSB-SC): here • the information signal is a “digital” waveform, which is determined by the constellation symbols and a pulse. 3 / 22 Up-converted PAM with a rectangular pulse 1 for t (0, T ] p(t) = √T ∈ { 0 otherwise is also called “Amplitude Shift Keying” (ASK). In this case, the transmitted passband waveform is x(t) = X p(t kT ) cos(2πf t) k − c ∑k 1 = Xk cos(2πfc t) for t [kT , (k + 1)T ) √T ∈ where X is chosen from a PAM constellation, say A, A . k {− } Note that a rectangular pulse (and consequently, ASK) is not bandwidth efficient. (You may encounter the terminology ASK in past Tripos questions. You will not be examined on it, but recognise that it is just up-converted PAM with a rectangular pulse shape.) 4 / 22 Demodulation of up-converted PAM at the Rx First, down-convert via product modulator + low-pass filter v(t) Low-pass y(t) y (t) × filter [−W; W ] b cos(2πfct) y (t) = x (t) + n (t) = X p(t kT ) + n (t) b b b k − b ∑k where nb(t) is baseband noise. Next demodulate baseband waveform yb(t). We already know how to do this: pass yb(t) through matched filter, and then sample at times mT m Z { } ∈ t = mT Filter r(t) yb(t) r(mT ) h(t) = p(−t) 5 / 22 Detection The sampled output of the matched filter at time mT is • Ym = Xm + Nm where N = n (τ)p(τ mT ) dτ (see prev. handout for details) m b − N is Gaussian∫ with zero mean and variance σ2 • m (σ2 can be empirically estimated) Maximum-likelihood detection: Choose Xˆ to be the • m constellation symbol closest to Ym 6 / 22 Spectrum of up-converted PAM The transmitted waveform x(t) = xb(t) cos(2πfc t) has spectrum 1 X (f ) = [X (f f ) + X (f + f )] 2 b − c b c Note that x (t) = X p(t kT ) b k − ∑k is a real signal since both the pulse p(t) and the symbols X are { k } real-valued X ( f ) = X (f ) ⇒ b − b∗ The spectrum X (f ) for f 0 determines X (f ) for f < 0 • ≥ jXb(f)j f −W 0 W Lower Sideband Upper Sideband jX(f)j −fc − W −fc −fc + W fc − W fc fc + W Sending both sidebands is redundant, since all the information • is contained in one 7 / 22 A bandwidth-efficient alternative to up-converted PAM One way to save bandwidth is to send only one sideband, just • like SSB-SC (see Amplitude Modulation handout) But since we are transmitting digital information, there is a • better way: make the information symbols complex-valued The baseband waveform is again x (t) = X p(t kT ) b k − ∑k but now the constellation from which the symbols Xk are drawn is complex-valued (i.e., Xk are now two-dimensional) xb(t) is now complex, but the passband signal we transmit has to be real. It is generated as j2πfc t x(t) = Re xb(t) e = Re([x (t))cos(2π]f t) Im(x (t))sin(2πf t) b c − b c This is called Quadrature Amplitude Modulation (QAM) 8 / 22 Quadrature Amplitude Modulation The upconverted QAM waveform that we transmit is x(t) = p(t kT )[Re(X ) cos(2πf t) Im(X ) sin(2πf t)] − k c − k c ∑k = p(t kT ) X cos(2πf t + ϕ ) − | k| c k ∑k where X and ϕ denote the magnitude and phase of the | k | k complex symbol Xk Thus, one can understand QAM in two ways: 1. QAM has two carriers, the cosine carries Re(Xk ) and the sin carries the Im(Xk ). 2. In QAM, the information symbol modulates both the amplitude and phase of the carrier; in up-converted PAM the information symbol is real and only modulates the amplitude Pulse shape p(t) is the same as that for PAM • The main difference between QAM and PAM is the • constellation. In PAM, Im(Xk ) = 0. 9 / 22 Some typical QAM Constellations Im(Xk) Im(Xk) Re(Xk) Re(Xk) −A A −A A BPSK QPSK −A A 8-PSK 16-QAM In “Phase Shift Keying”, the magnitude of Xk is constant, and the information is in the phase of the symbol. In an constellation with M symbols, each symbol corresponds to log M bits 2 10 / 22 Average Energy per Symbol Im(Xk) Re(Xk) −A A −A A −A A BPSK QPSK 8-PSK 2 For all the PSK constellations, average symbol energy Es = A Im(Xk) d Average energy per symbol for 16-QAM Re(X ) k 40d2 2 Es = 16 = 2.5d 16-QAM Average energy per bit E = E /log M b s 2 11 / 22 The transmitted waveform is x(t) = p(t kT ) X r cos(2πf t) X i sin(2πf t) − k c − k c k ∑ [ ] r i where Xk := Re(Xk ) and Xk := Im(Xk ) x(t) y(t) n(t) The energy per symbol is important because the power of • x(t) Es ∝ T At the Rx, we have to down-convert y(t) to a baseband • waveform via product modulators and low-pass filter For QAM, we need two product modulators, one for the • cosine and the other for sine 12 / 22 At the receiver, we have y(t) = p(t kT ) X r cos(2πf t) X i sin(2πf t) + n(t) − k c − k c k ∑ [ ] Low-pass y(t) yr(t) × filter [−W; W ] cos(2πfct) Low-pass y(t) yi(t) × filter [−W; W ] − sin(2πfct) After down-converting, we get y r (t) = X r p(t kT ) + nr (t) k − ∑k y i (t) = X i p(t kT ) + ni (t) k − ∑k where nr (t) and ni (t) are filtered (baseband) versions of n(t). Next perform matched-filter demodulation of y r (t) and y i (t) 13 / 22 Demodulation t = mT Filter r(t) yr(t) Y r h(t) = p(−t) m t = mT Filter r(t) yi(t) Y i h(t) = p(−t) m The sampled outputs of the matched filters for m = 0, 1,... • are: r r r Ym = Xm + Nm i i i Ym = Xm + Nm It can be shown that Nr and Ni are each independent • m m Gaussians distributed as (0, σ2) for each m N For each m, we now have to detect the complex-valued • r i r i constellation symbol Xm = (Xm, Xm) from Ym = (Ym, Ym) 14 / 22 Detection The discrete-time channel is Y = X + N where X , Y , N are now two-dimensional vectors, i.e., complex numbers with X = (X r , X i ) and Y = (Y r , Y i ) The optimal detection rule (assuming all constellation symbols are equally likely) is the maximum-likelihood detection rule Xˆ = arg max f (Y x) x | ∈C “Choose the symbol from which y is most likely to have occurred” The conditional distribution of Y = (Y r , Y i ) given x = (xr , xi ) is 1 (Y r xr )2/2σ2 1 (Y i xi )2/2σ2 f (Y x) = e− − e− − | √2πσ2 √2πσ2 1 [(Y r xr )2+(Y i xi )2]/2σ2 = 2πσ2 e− − − 15 / 22 The optimal detector is therefore Xˆ = arg min (Y r xr )2 + (Y i xi )2 = arg min Y x 2 x − − x | − | ∈C ∈C Choose the constellation symbol x closest to observed output Y (Same detection principle as PAM, but the symbols are complex in QAM) Example 1: The decision regions for QPSK Im(Y ) X^ = p1 p4 p1 A Re(Y ) p3 p2 16 / 22 Xˆ = arg min Y x 2 x | − | ∈C Example 2: The decision regions for 8-PSK Im(Y ) p7 p6 p8 X^ = p1 A Re(Y ) p5 p1 p4 p2 p3 Can similarly sketch the decision regions for other • constellations We can also calculate the probability of detection error • P = P(Xˆ = X ) for various constellations e ̸ 17 / 22 Im(Xk) Im(Xk) d d Re(Xk) Re(Xk) −A A 16-QAM 8-PSK We won’t do an exact calculation of QAM probability of error Pe , but can be shown that: P is a function depending on d , where d is the • e Q− σ separation between adjacent constellation points and σ2 is the variance of the Gaussian noise P decays exponentially with d2/σ2 • e Suppose we increase the number of constellation points, e.g., 16 QAM 64 QAM 256 QAM, while keeping E constant → → s (Es = average energy per symbol) : Transmission rate increases: 4 bits/symbol 6 bits/sym.
Load more

Recommended publications
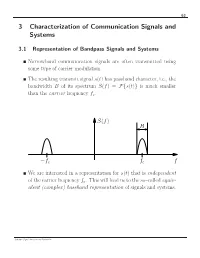
  • 3 Characterization of Communication Signals and Systems
    63 3 Characterization of Communication Signals and Systems 3.1 Representation of Bandpass Signals and Systems Narrowband communication signals are often transmitted using some type of carrier modulation. The resulting transmit signal s(t) has passband character, i.e., the bandwidth B of its spectrum S(f) = s(t) is much smaller F{ } than the carrier frequency fc. S(f) B f f f − c c We are interested in a representation for s(t) that is independent of the carrier frequency fc. This will lead us to the so–called equiv- alent (complex) baseband representation of signals and systems. Schober: Signal Detection and Estimation 64 3.1.1 Equivalent Complex Baseband Representation of Band- pass Signals Given: Real–valued bandpass signal s(t) with spectrum S(f) = s(t) F{ } Analytic Signal s+(t) In our quest to find the equivalent baseband representation of s(t), we first suppress all negative frequencies in S(f), since S(f) = S( f) is valid. − The spectrum S+(f) of the resulting so–called analytic signal s+(t) is defined as S (f) = s (t) =2 u(f)S(f), + F{ + } where u(f) is the unit step function 0, f < 0 u(f) = 1/2, f =0 . 1, f > 0 u(f) 1 1/2 f Schober: Signal Detection and Estimation 65 The analytic signal can be expressed as 1 s+(t) = − S+(f) F 1{ } = − 2 u(f)S(f) F 1{ } 1 = − 2 u(f) − S(f) F { } ∗ F { } 1 The inverse Fourier transform of − 2 u(f) is given by F { } 1 j − 2 u(f) = δ(t) + .
    [Show full text]
  • 2 the Wireless Channel
    CHAPTER 2 The wireless channel A good understanding of the wireless channel, its key physical parameters and the modeling issues, lays the foundation for the rest of the book. This is the goal of this chapter. A defining characteristic of the mobile wireless channel is the variations of the channel strength over time and over frequency. The variations can be roughly divided into two types (Figure 2.1): • Large-scale fading, due to path loss of signal as a function of distance and shadowing by large objects such as buildings and hills. This occurs as the mobile moves through a distance of the order of the cell size, and is typically frequency independent. • Small-scale fading, due to the constructive and destructive interference of the multiple signal paths between the transmitter and receiver. This occurs at the spatialscaleoftheorderofthecarrierwavelength,andisfrequencydependent. We will talk about both types of fading in this chapter, but with more emphasis on the latter. Large-scale fading is more relevant to issues such as cell-site planning. Small-scale multipath fading is more relevant to the design of reliable and efficient communication systems – the focus of this book. We start with the physical modeling of the wireless channel in terms of elec- tromagnetic waves. We then derive an input/output linear time-varying model for the channel, and define some important physical parameters. Finally, we introduce a few statistical models of the channel variation over time and over frequency. 2.1 Physical modeling for wireless channels Wireless channels operate through electromagnetic radiation from the trans- mitter to the receiver.
    [Show full text]
  • The Future of Passive Multiplexing & Multiplexing Beyond
    The Future of Passive Multiplexing & Multiplexing Beyond 10G From 1G to 10G was easy But Beyond 10G? 1G CWDM/DWDM 10G CWDM/DWDM 25G 40G Dark Fiber Passive Multiplexer 100G ? 400G Ingredients for Multiplexing 1) Dark Fiber 2) Multiplexers 3) Light : Transceivers Ingredients for Multiplexing 1) Dark Fiber 2 Multiplexer 3 Light + Transceiver Dark Fiber Attenuation → 0 km → → 40 km → → 80 km → Dispersion → 0 km → → 40 km → → 80 km → Dark Fiber Dispersion @1G DWDM max 200km → 0 km → → 40 km → → 80 km → @10G DWDM max 80km → 0 km → → 40 km → → 80 km → @25G DWDM max 15km → 0 km → → 40 km → → 80 km → Dark Fiber Attenuation → 80 km → 1310nm Window 1550nm/DWDM Dispersion → 80 km → Ingredients for Multiplexing 1 Dark FiBer 2) Multiplexers 3 Light + Transceiver Passive Mux Multiplexers 2 types • Cascaded TFF • AWG 95% of all Communication -Larger Multiplexers such as 40Ch/96Ch Multiplexers TFF: Thin film filter • Metal or glass tuBes 2cm*4mm • 3 fiBers: com / color / reflect • Each tuBe has 0.3dB loss • 95% of Muxes & OADM Multiplexers ABS casing Multiplexers AWG: arrayed wave grading -Larger muxes such as 40Ch/96Ch -Lower loss -Insertion loss 40ch = 3.0dB DWDM33 Transmission Window AWG Gaussian Fit Attenuation DWDM33 Low attenuation Small passband Reference passBand DWDM33 Isolation Flat Top Higher attenuation Wide passband DWDM light ALL TFF is Flat top Transmission Wave Types Flat Top: OK DWDM 10G Coherent 100G Gaussian Fit not OK DWDM PAM4 Ingredients for Multiplexing 1 Dark FiBer 2 Multiplexer 3) Light: Transceivers ITU Grids LWDM DWDM CWDM Attenuation
    [Show full text]
  • Performance Evaluation of Power-Line Communication Systems for LIN-Bus Based Data Transmission
    electronics Article Performance Evaluation of Power-Line Communication Systems for LIN-Bus Based Data Transmission Martin Brandl * and Karlheinz Kellner Department of Integrated Sensor Systems, Danube University, 3500 Krems, Austria; [email protected] * Correspondence: [email protected]; Tel.: +43-2732-893-2790 Abstract: Powerline communication (PLC) is a versatile method that uses existing infrastructure such as power cables for data transmission. This makes PLC an alternative and cost-effective technology for the transmission of sensor and actuator data by making dual use of the power line and avoiding the need for other communication solutions; such as wireless radio frequency communication. A PLC modem using DSSS (direct sequence spread spectrum) for reliable LIN-bus based data transmission has been developed for automotive applications. Due to the almost complete system implementation in a low power microcontroller; the component cost could be radically reduced which is a necessary requirement for automotive applications. For performance evaluation the DSSS modem was compared to two commercial PLC systems. The DSSS and one of the commercial PLC systems were designed as a direct conversion receiver; the other commercial module uses a superheterodyne architecture. The performance of the systems was tested under the influence of narrowband interference and additive Gaussian noise added to the transmission channel. It was found that the performance of the DSSS modem against singleton interference is better than that of commercial PLC transceivers by at least the processing gain. The performance of the DSSS modem was at least 6 dB better than the other modules tested under the influence of the additive white Gaussian noise on the transmission channel at data rates of 19.2 kB/s.
    [Show full text]
  • Passband Data Transmission I Introduction in Digital Passband
    Passband Data Transmission I References Phase-shift keying Chapter 4.1-4.3, S. Haykin, Communication Systems, Wiley. J.1 Introduction In baseband pulse transmission, a data stream represented in the form of a discrete pulse-amplitude modulated (PAM) signal is transmitted over a low- pass channel. In digital passband transmission, the incoming data stream is modulated onto a carrier with fixed frequency and then transmitted over a band-pass channel. J.2 1 Passband digital transmission allows more efficient use of the allocated RF bandwidth, and flexibility in accommodating different baseband signal formats. Example Mobile Telephone Systems GSM: GMSK modulation is used (a variation of FSK) IS-54: π/4-DQPSK modulation is used (a variation of PSK) J.3 The modulation process making the transmission possible involves switching (keying) the amplitude, frequency, or phase of a sinusoidal carrier in accordance with the incoming data. There are three basic signaling schemes: Amplitude-shift keying (ASK) Frequency-shift keying (FSK) Phase-shift keying (PSK) J.4 2 ASK PSK FSK J.5 Unlike ASK signals, both PSK and FSK signals have a constant envelope. PSK and FSK are preferred to ASK signals for passband data transmission over nonlinear channel (amplitude nonlinearities) such as micorwave link and satellite channels. J.6 3 Classification of digital modulation techniques Coherent and Noncoherent Digital modulation techniques are classified into coherent and noncoherent techniques, depending on whether the receiver is equipped with a phase- recovery circuit or not. The phase-recovery circuit ensures that the local oscillator in the receiver is synchronized to the incoming carrier wave (in both frequency and phase).
    [Show full text]
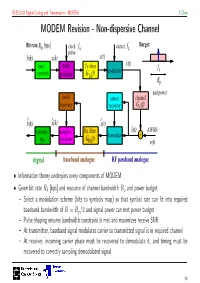
  • MODEM Revision
    ELEC3203 Digital Coding and Transmission – MODEM S Chen MODEM Revision - Non-dispersive Channel Burget: Bit rate:Rb [bps] clock fs carrier fc pulse b(k) x(k) x(t) bits / pulse Tx filter s(t) modulator fc symbols generator GTx (f) Bp and power clock carrier channel recovery recovery G c (f) b(k)^ x(k)^ x(t)^ symbols / sampler / Rx filter s(t)^ AWGN demodulat + bits decision GRx (f) n(t) digital baseband analogue RF passband analogue • Information theory underpins every components of MODEM • Given bit rate Rb [bps] and resource of channel bandwidth Bp and power budget – Select a modulation scheme (bits to symbols map) so that symbol rate can fit into required baseband bandwidth of B = Bp/2 and signal power can met power budget – Pulse shaping ensures bandwidth constraint is met and maximizes receive SNR – At transmitter, baseband signal modulates carrier so transmitted signal is in required channel – At receiver, incoming carrier phase must be recovered to demodulate it, and timing must be recovered to correctly sampling demodulated signal 94 ELEC3203 Digital Coding and Transmission – MODEM S Chen MODEM Revision - Dispersive Channel • For dispersive channel, equaliser at receiver aims to make combined channel/equaliser a Nyquist system again + = bandwidth bandwidth channel equaliser combined – Design of equaliser is a trade off between eliminating ISI and not enhancing noise too much • Generic framework of adaptive equalisation with training and decision-directed modes n[k] x[k] y[k] f[k] x[k−k^ ] Σ equaliser decision d channel circuit − Σ
    [Show full text]
  • Analysis of the PAPR Behavior of the OFDM Passband Signal
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 19 December 2019 doi:10.20944/preprints201912.0255.v1 Article Analysis of the PAPR Behavior of the OFDM Passband Signal Frank Andrés Eras 0000-0002-7844-5670, Italo Alexander Carreño, Thomas Borja, Diego Javier Reinoso* 0000-0003-0854-1250, Luis Felipe Urquiza 0000-0002-6405-2067, Martha Cecilia Paredes 0000-0001-5789-4568 Departamento de Electrónica, Telecomunicaciones y Redes de Información, Escuela Politécnica Nacional * Correspondence: [email protected] 1 Abstract: Orthogonal Frequency Division Multiplexing (OFDM) is a technique widely used in today’s 2 wireless communication systems due to its ability to combat the effects of multi-path in the signal. 3 However, one of the main limitations of the use of OFDM is its high Peak-to-Average Power Ratio 4 (PAPR), which reduces the efficiency of the OFDM system. The effects of PAPR can produce both 5 out-of-band and in-band radiation, which degrades the signal by increasing the bit error rate (BER), 6 this occurs in both baseband and bandpass sginals. In this document the effect of the PAPR in a 7 OFDM passband signal is analyzed considering the implementation of a High Power Amplifier (HPA) 8 and the Simple Amplitude Predistortion-Orthogonal Pilot Sequences (OPS-SAP) scheme to reduce 9 the PAPR. 10 Keywords: OFDM; PAPR; passband; IEEE 802.11p 11 1. Introduction 12 For some years, many wireless communication systems have based the transmission of 13 information on the Orthogonal Frequency Division Multiplexing (OFDM) scheme, which is used 14 in standards such as Long-Term Evolution (LTE), Wireless Local Area Networks (WLAN), Digital 15 Video Broadcasting (DVB-T), among others.
    [Show full text]
  • Quantum Key Distribution for 10 Gb/S Dense Wavelength Division Multiplexing Networks K
    Quantum key distribution for 10 Gb/s dense wavelength division multiplexing networks K. A. Patel,1,2 J. F. Dynes,1 M. Lucamarini,1 I. Choi,1 A. W. Sharpe,1 Z. L. Yuan,1 R. V. Penty2 and A. J. Shields1 1Toshiba Research Europe Limited, Cambridge Research Laboratory, 208 Cambridge Science Park, Milton Road, Cambridge, CB4 0GZ, United Kingdom 2Cambridge University Engineering Department, 9 J J Thomson Avenue, Cambridge, CB3 0FA, United Kingdom Abstract: We demonstrate quantum key distribution (QKD) with bidirectional 10 Gb/s classical data channels in a single fiber using dense wavelength division multiplexing. Record secure key rates of 2.38 Mbps and fiber distances up to 70 km are achieved. Data channels are simultaneously monitored for error-free operation. The robustness of QKD is further demonstrated with a secure key rate of 445 kbps over 25 km, obtained in the presence of data lasers launching conventional 0 dBm power. We discuss the fundamental limit for the QKD performance in the multiplexing environment. 1 Quantum key distribution (QKD)1 is revolutionizing the way of distributing secret cryptographic keys for information protection. Unlike its classical counterparts, it allows secure transmission of information with quantifiable security2-4 and detection of an eavesdropper. After numerous experiments in the laboratory4-7 as well as in field,8,9 the technology has matured for deployment on dark fiber with secure key rates exceeding 1 Mb/s. Nevertheless, for wider adoption, QKD must adapt to existing fiber infrastructures, which are populated with classical data communications. Quantum and classical data signals can be combined onto a single fiber using wavelength division multiplexing.
    [Show full text]
  • Fundamentals of Spread-Spectrum Techniques
    RGHEFF CH003.tex 13/6/2007 17: 33 Page 153 3 Fundamentals of spread-spectrum techniques In this chapter we consider the spread-spectrum transmission schemes that demand channel bandwidth much greater than is required by the Nyquist sampling theorem. You will recall from Chapter 2 that the minimum bandpass bandwidth required for data transmission through an ideal channel is equal to the data symbol rate.You will also recall that wideband reception allows a large amount of input noise power to the detector and thus degrades the quality of the detected data. Therefore, the receivers for spread-spectrum schemes have to convert the received wideband signals back to their original narrowband waveforms before detection. This process generates a certain amount of processing gain that can be used to combat radio jamming and interference. We will describe and discuss in detail the properties and methods of generation of the functions used in creating wide spectrum signals. Finally, we consider the multiple access properties of the spread-spectrum systems and outline the analytical model for evaluating the system performance. 3.1 Historical background There was intensive use of communications warfare during World War II. This technique outlined the ability to intercept and interfere with hostile communications. Consequently, this procedure stimulated a great deal of interest which led to the development of secure communications systems and work in this field was carried out on two fronts. Firstly, development in communication theory initiated encryption schemes (Shannon, 1949) to provide certain information protection. Secondly, work was initiated to harness the devel- opment of a new technology.
    [Show full text]
  • Quadrature Amplitude Modulation (QAM)
    Quadrature Amplitude Modulation (QAM) PAM signals occupy twice the bandwidth required for the baseband Transmit two PAM signals using carriers of the same frequency but in phase and quadrature Demodulation: QAM Transmitter Implementation QAM is widely used method for transmitting digital data over bandpass channels A basic QAM transmitter Inphase component Pulse a Impulse a*(t) a(t) n Shaping Modulator + d Map to Filter sin w t n Serial to c Constellation g (t) s(t) Parallel T Point * Pulse 1 Impulse b (t) b(t) Shaping - J Modulator bn Filter quadrature component gT(t) cos wct Using complex notation = − = ℜ s(t) a(t)cos wct b(t)sin wct s(t) {s+ (t)} which is the preenvelope of QAM ∞ ∞ − = + − jwct = jwckT − jwc (t kT ) s+ (t) (ak jbk )gT (t kT )e s+ (t) (ck e )gT (t kT)e −∞ −∞ Complex Symbols Quadriphase-Shift Keying (QPSK) 4-QAM Transmitted signal is contained in the phase imaginary imaginary real real M-ary PSK QPSK is a special case of M-ary PSK, where the phase of the carrier takes on one of M possible values imaginary real Pulse Shaping Filters The real pulse shaping g (t) filter response T = jwct = + Let h(t) gT (t)e hI (t) jhQ (t) = hI (t) gT (t)cos wct = where hQ (t) gT (t)sin wct = − This filter is a bandpass H (w) GT (w wc ) filter with the frequency response Transmitted Sequences Modulated sequences before passband shaping ' = ℜ jwc kT = − ak {ck e } ak cos wc kT bk sin wc kT ' = ℑ jwc kT = + bk {ck e } ak sin wc kT bk cos wc kT Using these definitions ∞ = ℜ = ' − − ' − s(t) {s+ (t)} ak hI (t kT) bk hQ (t kT)
    [Show full text]
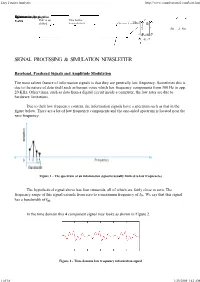
  • Easy Fourier Analysis
    Easy Fourier Analysis http://www.complextoreal.com/base.htm SpectrumDCInformationSignal term at 2w on csignal the positivenegative x-axis Half is up This half is shifted. down shifted. Charan Langton, The Carrier Editor fm = -1 fm = -9, fc-9,-9 -8, = -8, -8-7 -7 -9, -8, -7 SIGNAL PROCESSING & SIMULATION NEWSLETTER Baseband, Passband Signals and Amplitude Modulation The most salient feature of information signals is that they are generally low frequency. Sometimes this is due to the nature of data itself such as human voice which has frequency components from 300 Hz to app. 20 KHz. Other times, such as data from a digital circuit inside a computer, the low rates are due to hardware limitations. Due to their low frequency content, the information signals have a spectrum such as that in the figure below. There are a lot of low frequency components and the one-sided spectrum is located near the zero frequency. Figure 1 - The spectrum of an information signal is usually limited to low frequencies The hypothetical signal above has four sinusoids, all of which are fairly close to zero. The frequency range of this signal extends from zero to a maximum frequency of fm. We say that this signal has a bandwidth of fm. In the time domain this 4 component signal may looks as shown in Figure 2. Figure 2 - Time domain low frequency information signal 1 of 18 1/25/2008 3:42 AM Easy Fourier Analysis http://www.complextoreal.com/base.htm Now let’s modulate this signal, which means we are going to transfer it to a higher (usually much higher) frequency.
    [Show full text]
  • OFDM) and Advanced Signal Processing for Elastic Optical Networking in Accordance with Networking and Transmission Constraints
    Implementation of Orthogonal Frequency Division Multiplexing (OFDM) and Advanced Signal Processing for Elastic Optical Networking in Accordance with Networking and Transmission Constraints Item Type text; Electronic Dissertation Authors Johnson, Stanley Publisher The University of Arizona. Rights Copyright © is held by the author. Digital access to this material is made possible by the University Libraries, University of Arizona. Further transmission, reproduction or presentation (such as public display or performance) of protected items is prohibited except with permission of the author. Download date 09/10/2021 15:31:10 Link to Item http://hdl.handle.net/10150/612584 IMPLEMENTATION OF ORTHOGONAL FREQUENCY DIVISION MULTIPLEXING (OFDM) AND ADVANCED SIGNAL PROCESSING FOR ELASTIC OPTICAL NETWORKING IN ACCORDANCE WITH NETWORKING AND TRANSMISSION CONSTRAINTS by Stanley Johnson _____________________ Copyright © Stanley Johnson 2016 A Dissertation Submitted to the Faculty of the COLLEGE OF OPTICAL SCIENCES In Partial Fulfillment of the Requirements For the Degree of DOCTOR OF PHILOSOPHY In the Graduate College THE UNIVERSITY OF ARIZONA 2 0 1 6 2 THE UNIVERSITY OF ARIZONA GRADUATE COLLEGE As members of the Dissertation Committee, we certify that we have read the dissertation prepared by Stanley Johnson, titled Implementation of Orthogonal Frequency Division Multiplexing (OFDM) and Advanced Signal Processing for Elastic Optical Networking in Accordance with Networking and Transmission Constraints and recommend that it be accepted as fulfilling
    [Show full text]