DOCSLIB.ORG

Analog Lowpass Filter Specifications

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Analog Lowpass Filter Specifications Analog Lowpass Filter Analog Lowpass Filter Specifications Specifications • Typical magnitude response H a ( j Ω ) of an •In the passband, defined by 0 ≤ Ω ≤ Ω p , we analog lowpass filter may be given as require indicated below 1− δ p ≤ Ha ( jΩ) ≤1+ δ p , Ω ≤ Ω p i.e., H a ( j Ω ) approximates unity within an error of ± δ p •In the stopband, defined by Ω s ≤ Ω ≤ ∞ , we require Ha ( jΩ) ≤ δs , Ωs ≤ Ω ≤ ∞ i.e., H a ( j Ω ) approximates zero within an 1 2 error of δs Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Analog Lowpass Filter Analog Lowpass Filter Specifications Specifications • Ω p - passband edge frequency • Magnitude specifications may alternately be •-Ωs stopband edge frequency given in a normalized form as indicated •-δ p peak ripple value in the passband below •-δs peak ripple value in the stopband • Peak passband ripple α p = −20log10 (1− δ p ) dB • Minimum stopband attenuation αs = −20log10(δs ) dB 3 4 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Analog Lowpass Filter Analog Lowpass Filter Design Specifications • Two additional parameters are defined - • Here, the maximum value of the magnitude in the passband assumed to be unity Ω (1) Transition ratio k = p Ωs •-1/ 1+ ε 2 Maximum passband deviation, given by the minimum value of the For a lowpass filter k <1 magnitude in the passband ε (2) Discrimination parameter k = 1 A2 −1 •-1 Maximum stopband magnitude Usually k <<1 A 1 5 6 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra 1 Butterworth Approximation Butterworth Approximation • The magnitude-square response of an N-th order analog lowpass Butterworth filter 2 is given by • Gain in dB is G(Ω) =10log10 Ha ( jΩ) 2 1 Ha ( jΩ) = 2N 1+ (Ω/ Ωc ) • As G ( 0 ) = 0 and 2 • First 2 N − 1 derivatives of H a ( j Ω ) at Ω = 0 G(Ωc ) =10log10 (0.5) = −3.0103 ≅ −3dB are equal to zero Ωc is called the 3-dB cutoff frequency • The Butterworth lowpass filter thus is said to have a maximally-flat magnitude at Ω = 0 7 8 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Butterworth Approximation Butterworth Approximation • Typical magnitude responses with Ωc =1 • Two parameters completely characterizing a Butterworth Filter Butterworth lowpass filter are Ω c and N N = 2 • These are determined from the specified 1 N = 4 0.8 N = 10 bandedgesΩ p and Ω s , and minimum 2 nitude 0.6 g passband magnitude 1 / 1 + ε , and Ma 0.4 maximum stopband ripple 1/ A 0.2 0 0 1 2 3 Ω 9 10 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Butterworth Approximation Butterworth Approximation • Since order N must be an integer, value • Ω and N are thus determined from c obtained is rounded up to the next highest 2 1 1 Ha ( jΩ p ) = = integer 1+ (Ω / Ω )2N 1+ ε 2 p c • This value of N is used next to determine Ω 2 1 1 c H ( jΩ ) = = by satisfying either the stopband edge or the a s 1+ (Ω / Ω )2N A2 s c passband edge specification exactly • Solving the above we get • If the stopband edge specification is log [(A2 −1)/ε 2 ] log (1/ k ) satisfied, then the passband edge N = 1⋅ 10 = 10 1 specification is exceeded providing a safety 2 log (Ω / Ω ) log (1/ k) 10 s p 10 margin 11 12 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra 2 Butterworth Approximation Butterworth Approximation •Example- Determine the lowest order of a • Transfer function of an analog Butterworth Butterworth lowpass filter with a 1-dB cutoff lowpass filter is given by frequency at 1 kHz and a minimum attenuation of 40 dB at 5 kHz ΩN ΩN H (s) = C = c = c •Now a D (s) N N −1 l N ⎛ 1 ⎞ N s + ∑ =0 d s ∏ =1(s − p ) 10log ⎜ ⎟ = −1 l l l l 10⎝1+ ε 2 ⎠ where which yields ε 2 = 0.25895 j[π (N +2l−1) / 2N ] p = Ωce , 1≤ l ≤ N l and ⎛ 1 ⎞ • Denominator D ( s ) is known as the 10log ⎜ ⎟ = −40 N 10 A2 Butterworth polynomial of order N ⎝ ⎠ which yields A2 =10,000 13 14 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Butterworth Approximation Chebyshev Approximation 2 • The magnitude-square response of an N-th • Therefore 1 = A −1 =196.51334 k ε order analog lowpass Type 1 Chebyshev filter 1 is given by 1 Ωs and = = 5 2 1 k H (s) = Ω p a 2 2 1+ ε TN (Ω / Ω p ) • Hence where T N ( Ω ) is the Chebyshev polynomial log (1/ k ) of order N: N = 10 1 = 3.2811 log10 (1/ k) ⎧ cos(N cos−1 Ω), Ω ≤1 TN (Ω) = ⎨ −1 • We choose N = 4 ⎩cosh(N cosh Ω), Ω >1 15 16 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Chebyshev Approximation Chebyshev Approximation • If at Ω = Ω s the magnitude is equal to 1/A, • Typical magnitude response plots of the then analog lowpass Type 1 Chebyshev filter are 2 1 1 shown below Ha ( jΩs ) = 2 2 = 2 Type 1 Chebyshev Filter 1+ ε TN (Ωs / Ω p ) A N = 2 1 N = 3 • Solving the above we get 0.8 N = 8 −1 2 −1 cosh ( A −1/ε) cosh (1/ k1) nitude 0.6 g N = −1 = −1 Ma 0.4 cosh (Ωs / Ω p ) cosh (1/ k) 0.2 •Order N is chosen as the nearest integer 0 0 1 2 3 greater than or equal to the above value Ω 17 18 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra 3 Chebyshev Approximation Chebyshev Approximation • The magnitude-square response of an N-th • Typical magnitude response plots of the order analog lowpass Type 2 Chebyshev analog lowpass Type 2 Chebyshev filter are (also called inverse Chebyshev) filter is shown below given by Type 2 Chebyshev Filter 2 1 N = 3 H ( jΩ) = 1 N = 5 a 2 0.8 N = 7 2 ⎡TN (Ωs / Ω p )⎤ nitude 0.6 1+ ε ⎢ ⎥ g ⎣ TN (Ωs / Ω) ⎦ Ma 0.4 0.2 where T N ( Ω ) is the Chebyshev polynomial 0 0 1 2 3 of order N Ω 19 20 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Chebyshev Approximation Elliptic Approximation • The order N of the Type 2 Chebyshev filter • The square-magnitude response of an is determined from given ε , , and A elliptic lowpass filter is given by Ωs using 2 1 −1 2 −1 cosh ( A −1/ε) cosh (1/ k ) Ha ( jΩ) = 2 2 1 1+ ε R (Ω/ Ω ) N = −1 = −1 N p cosh (Ωs / Ω p ) cosh (1/ k) where R N ( Ω ) is a rational function of order •Example- Determine the lowest order of a N satisfying R ( 1 / Ω ) = 1 / R ( Ω ) , with the Chebyshev lowpass filter with a 1-dB cutoff N N frequency at 1 kHz and a minimum attenuation of roots of its numerator lying in the interval 40 dB at 5 kHz - 0 < Ω <1 and the roots of its denominator −1 lying in the interval 1< Ω < ∞ cosh (1/ k1) N = −1 = 2.6059 21 cosh (1/ k) 22 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Elliptic Approximation Elliptic Approximation • For given Ω p , Ω s , ε , and A, the filter order • Example - Determine the lowest order of a elliptic can be estimated using lowpass filter with a 1-dB cutoff frequency at 1 2 log (4/ k ) kHz and a minimum attenuation of 40 dB at 5 kHz N 10 1 ≅ 1/ k =196.5134 log10 (1/ ρ) Note: k = 0.2 and 1 where k'= 1− k 2 • Substituting these values we get k'= 0.979796, ρ0 = 0.00255135, ρ = 1− k' 0 2(1+ k') ρ = 0.0025513525 5 9 13 ρ = ρ0 + 2(ρ0 ) +15(ρ0 ) +150(ρ0 ) • and hence N = 2.23308 • Choose N = 3 23 24 Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra 4 Analog Lowpass Filter Design Elliptic Approximation •Example- Design an elliptic lowpass filter of lowest order with a 1-dB cutoff • Typical magnitude response plots with Ω p = 1 frequency at 1 kHz and a minimum are shown below attenuation of 40 dB at 5 kHz Elliptic Filter • Code fragments used N = 3 1 N = 4 [N, Wn] = ellipord(Wp, Ws, Rp, Rs, ‘s’); 0.8 [b, a] = ellip(N, Rp, Rs, Wn, ‘s’); nitude 0.6 g Ma 0.4 with Wp = 2*pi*1000; 0.2 Ws = 2*pi*5000; 0 0 1 2 3 Rp = 1; Ω 25 26 Rs = 40; Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Design of Analog Highpass, Analog Lowpass Filter Design Bandpass and Bandstop Filters • Steps involved in the design process: • Gain plot Step 1 - Develop of specifications of a Lowpass Elliptic Filter prototype analog lowpass filter H L P ( s ) 0 from specifications of desired analog filter -20 HD (s) using a frequency transformation Step 2 - Design the prototype analog Gain, dB -40 lowpass filter -60 Step 3 - Determine the transfer function H (s) 0 2000 4000 6000 D Frequency, Hz of desired analog filter by applying the inverse frequency transformation to H (s) 27 28 LP Copyright © 2005, S. K. Mitra Copyright © 2005, S. K. Mitra Design of Analog Highpass, Analog Highpass Filter Design Bandpass and Bandstop Filters •Let s denote the Laplace transform variable • Spectral Transformation: of prototype analog lowpass filter H (s) Ω Ωˆ LP s = p p and sˆ denote the Laplace transform sˆ variable of desired analog filter H (sˆ) D where Ω is the passband edge frequency of • The mapping from s-domain to -domain is p sˆ H (s) and Ωˆ is the passband edge given by the invertible transformation LP p frequency of H (sˆ) s = F(sˆ) HP • On the imaginary axis the transformation is •Then H (sˆ) = H (s) D LP s=F (sˆ) ˆ Ω pΩ p H (s) = H (sˆ) −1 Ω = − LP D sˆ=F (s) Ωˆ 29 30 Copyright © 2005, S.
Load more

Recommended publications
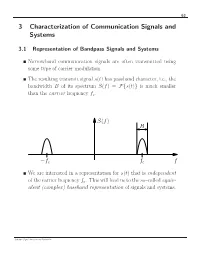
  • 3 Characterization of Communication Signals and Systems
    63 3 Characterization of Communication Signals and Systems 3.1 Representation of Bandpass Signals and Systems Narrowband communication signals are often transmitted using some type of carrier modulation. The resulting transmit signal s(t) has passband character, i.e., the bandwidth B of its spectrum S(f) = s(t) is much smaller F{ } than the carrier frequency fc. S(f) B f f f − c c We are interested in a representation for s(t) that is independent of the carrier frequency fc. This will lead us to the so–called equiv- alent (complex) baseband representation of signals and systems. Schober: Signal Detection and Estimation 64 3.1.1 Equivalent Complex Baseband Representation of Band- pass Signals Given: Real–valued bandpass signal s(t) with spectrum S(f) = s(t) F{ } Analytic Signal s+(t) In our quest to find the equivalent baseband representation of s(t), we first suppress all negative frequencies in S(f), since S(f) = S( f) is valid. − The spectrum S+(f) of the resulting so–called analytic signal s+(t) is defined as S (f) = s (t) =2 u(f)S(f), + F{ + } where u(f) is the unit step function 0, f < 0 u(f) = 1/2, f =0 . 1, f > 0 u(f) 1 1/2 f Schober: Signal Detection and Estimation 65 The analytic signal can be expressed as 1 s+(t) = − S+(f) F 1{ } = − 2 u(f)S(f) F 1{ } 1 = − 2 u(f) − S(f) F { } ∗ F { } 1 The inverse Fourier transform of − 2 u(f) is given by F { } 1 j − 2 u(f) = δ(t) + .
    [Show full text]
  • 2 the Wireless Channel
    CHAPTER 2 The wireless channel A good understanding of the wireless channel, its key physical parameters and the modeling issues, lays the foundation for the rest of the book. This is the goal of this chapter. A defining characteristic of the mobile wireless channel is the variations of the channel strength over time and over frequency. The variations can be roughly divided into two types (Figure 2.1): • Large-scale fading, due to path loss of signal as a function of distance and shadowing by large objects such as buildings and hills. This occurs as the mobile moves through a distance of the order of the cell size, and is typically frequency independent. • Small-scale fading, due to the constructive and destructive interference of the multiple signal paths between the transmitter and receiver. This occurs at the spatialscaleoftheorderofthecarrierwavelength,andisfrequencydependent. We will talk about both types of fading in this chapter, but with more emphasis on the latter. Large-scale fading is more relevant to issues such as cell-site planning. Small-scale multipath fading is more relevant to the design of reliable and efficient communication systems – the focus of this book. We start with the physical modeling of the wireless channel in terms of elec- tromagnetic waves. We then derive an input/output linear time-varying model for the channel, and define some important physical parameters. Finally, we introduce a few statistical models of the channel variation over time and over frequency. 2.1 Physical modeling for wireless channels Wireless channels operate through electromagnetic radiation from the trans- mitter to the receiver.
    [Show full text]
  • Frequency Response
    EE105 – Fall 2015 Microelectronic Devices and Circuits Frequency Response Prof. Ming C. Wu [email protected] 511 Sutardja Dai Hall (SDH) Amplifier Frequency Response: Lower and Upper Cutoff Frequency • Midband gain Amid and upper and lower cutoff frequencies ωH and ω L that define bandwidth of an amplifier are often of more interest than the complete transferfunction • Coupling and bypass capacitors(~ F) determineω L • Transistor (and stray) capacitances(~ pF) determineω H Lower Cutoff Frequency (ωL) Approximation: Short-­Circuit Time Constant (SCTC) Method 1. Identify all coupling and bypass capacitors 2. Pick one capacitor ( ) at a time, replace all others with short circuits 3. Replace independent voltage source withshort , and independent current source withopen 4. Calculate the resistance ( ) in parallel with 5. Calculate the time constant, 6. Repeat this for each of n the capacitor 7. The low cut-­off frequency can be approximated by n 1 ωL ≅ ∑ i=1 RiSCi Note: this is an approximation. The real low cut-­off is slightly lower Lower Cutoff Frequency (ωL) Using SCTC Method for CS Amplifier SCTC Method: 1 n 1 fL ≅ ∑ 2π i=1 RiSCi For the Common-Source Amplifier: 1 # 1 1 1 & fL ≅ % + + ( 2π $ R1SC1 R2SC2 R3SC3 ' Lower Cutoff Frequency (ωL) Using SCTC Method for CS Amplifier Using the SCTC method: For C2 : = + = + 1 " 1 1 1 % R3S R3 (RD RiD ) R3 (RD ro ) fL ≅ $ + + ' 2π # R1SC1 R2SC2 R3SC3 & For C1: R1S = RI +(RG RiG ) = RI + RG For C3 : 1 R2S = RS RiS = RS gm Design: How Do We Choose the Coupling and Bypass Capacitor Values? • Since the impedance of a capacitor increases with decreasing frequency, coupling/bypass capacitors reduce amplifier gain at low frequencies.
    [Show full text]
  • Classic Filters There Are 4 Classic Analogue Filter Types: Butterworth, Chebyshev, Elliptic and Bessel. There Is No Ideal Filter
    Classic Filters There are 4 classic analogue filter types: Butterworth, Chebyshev, Elliptic and Bessel. There is no ideal filter; each filter is good in some areas but poor in others. • Butterworth: Flattest pass-band but a poor roll-off rate. • Chebyshev: Some pass-band ripple but a better (steeper) roll-off rate. • Elliptic: Some pass- and stop-band ripple but with the steepest roll-off rate. • Bessel: Worst roll-off rate of all four filters but the best phase response. Filters with a poor phase response will react poorly to a change in signal level. Butterworth The first, and probably best-known filter approximation is the Butterworth or maximally-flat response. It exhibits a nearly flat passband with no ripple. The rolloff is smooth and monotonic, with a low-pass or high- pass rolloff rate of 20 dB/decade (6 dB/octave) for every pole. Thus, a 5th-order Butterworth low-pass filter would have an attenuation rate of 100 dB for every factor of ten increase in frequency beyond the cutoff frequency. It has a reasonably good phase response. Figure 1 Butterworth Filter Chebyshev The Chebyshev response is a mathematical strategy for achieving a faster roll-off by allowing ripple in the frequency response. As the ripple increases (bad), the roll-off becomes sharper (good). The Chebyshev response is an optimal trade-off between these two parameters. Chebyshev filters where the ripple is only allowed in the passband are called type 1 filters. Chebyshev filters that have ripple only in the stopband are called type 2 filters , but are are seldom used.
    [Show full text]
  • The Future of Passive Multiplexing & Multiplexing Beyond
    The Future of Passive Multiplexing & Multiplexing Beyond 10G From 1G to 10G was easy But Beyond 10G? 1G CWDM/DWDM 10G CWDM/DWDM 25G 40G Dark Fiber Passive Multiplexer 100G ? 400G Ingredients for Multiplexing 1) Dark Fiber 2) Multiplexers 3) Light : Transceivers Ingredients for Multiplexing 1) Dark Fiber 2 Multiplexer 3 Light + Transceiver Dark Fiber Attenuation → 0 km → → 40 km → → 80 km → Dispersion → 0 km → → 40 km → → 80 km → Dark Fiber Dispersion @1G DWDM max 200km → 0 km → → 40 km → → 80 km → @10G DWDM max 80km → 0 km → → 40 km → → 80 km → @25G DWDM max 15km → 0 km → → 40 km → → 80 km → Dark Fiber Attenuation → 80 km → 1310nm Window 1550nm/DWDM Dispersion → 80 km → Ingredients for Multiplexing 1 Dark FiBer 2) Multiplexers 3 Light + Transceiver Passive Mux Multiplexers 2 types • Cascaded TFF • AWG 95% of all Communication -Larger Multiplexers such as 40Ch/96Ch Multiplexers TFF: Thin film filter • Metal or glass tuBes 2cm*4mm • 3 fiBers: com / color / reflect • Each tuBe has 0.3dB loss • 95% of Muxes & OADM Multiplexers ABS casing Multiplexers AWG: arrayed wave grading -Larger muxes such as 40Ch/96Ch -Lower loss -Insertion loss 40ch = 3.0dB DWDM33 Transmission Window AWG Gaussian Fit Attenuation DWDM33 Low attenuation Small passband Reference passBand DWDM33 Isolation Flat Top Higher attenuation Wide passband DWDM light ALL TFF is Flat top Transmission Wave Types Flat Top: OK DWDM 10G Coherent 100G Gaussian Fit not OK DWDM PAM4 Ingredients for Multiplexing 1 Dark FiBer 2 Multiplexer 3) Light: Transceivers ITU Grids LWDM DWDM CWDM Attenuation
    [Show full text]
  • Performance Evaluation of Power-Line Communication Systems for LIN-Bus Based Data Transmission
    electronics Article Performance Evaluation of Power-Line Communication Systems for LIN-Bus Based Data Transmission Martin Brandl * and Karlheinz Kellner Department of Integrated Sensor Systems, Danube University, 3500 Krems, Austria; [email protected] * Correspondence: [email protected]; Tel.: +43-2732-893-2790 Abstract: Powerline communication (PLC) is a versatile method that uses existing infrastructure such as power cables for data transmission. This makes PLC an alternative and cost-effective technology for the transmission of sensor and actuator data by making dual use of the power line and avoiding the need for other communication solutions; such as wireless radio frequency communication. A PLC modem using DSSS (direct sequence spread spectrum) for reliable LIN-bus based data transmission has been developed for automotive applications. Due to the almost complete system implementation in a low power microcontroller; the component cost could be radically reduced which is a necessary requirement for automotive applications. For performance evaluation the DSSS modem was compared to two commercial PLC systems. The DSSS and one of the commercial PLC systems were designed as a direct conversion receiver; the other commercial module uses a superheterodyne architecture. The performance of the systems was tested under the influence of narrowband interference and additive Gaussian noise added to the transmission channel. It was found that the performance of the DSSS modem against singleton interference is better than that of commercial PLC transceivers by at least the processing gain. The performance of the DSSS modem was at least 6 dB better than the other modules tested under the influence of the additive white Gaussian noise on the transmission channel at data rates of 19.2 kB/s.
    [Show full text]
  • Feedback Amplifiers
    UNIT II FEEDBACK AMPLIFIERS & OSCILLATORS FEEDBACK AMPLIFIERS: Feedback concept, types of feedback, Amplifier models: Voltage amplifier, current amplifier, trans-conductance amplifier and trans-resistance amplifier, feedback amplifier topologies, characteristics of negative feedback amplifiers, Analysis of feedback amplifiers, Performance comparison of feedback amplifiers. OSCILLATORS: Principle of operation, Barkhausen Criterion, types of oscillators, Analysis of RC-phase shift and Wien bridge oscillators using BJT, Generalized analysis of LC Oscillators, Hartley and Colpitts’s oscillators with BJT, Crystal oscillators, Frequency and amplitude stability of oscillators. 1.1 Introduction: Feedback Concept: Feedback: A portion of the output signal is taken from the output of the amplifier and is combined with the input signal is called feedback. Need for Feedback: • Distortion should be avoided as far as possible. • Gain must be independent of external factors. Concept of Feedback: Block diagram of feedback amplifier consist of a basic amplifier, a mixer (or) comparator, a sampler, and a feedback network. Figure 1.1 Block diagram of an amplifier with feedback A – Gain of amplifier without feedback. A = X0 / Xi Af – Gain of amplifier with feedback.Af = X0 / Xs β – Feedback ratio. β = Xf / X0 X is either voltage or current. 1.2 Types of Feedback: 1. Positive feedback 2. Negative feedback 1.2.1 Positive Feedback: If the feedback signal is in phase with the input signal, then the net effect of feedback will increase the input signal given to the amplifier. This type of feedback is said to be positive or regenerative feedback. Xi=Xs+Xf Af = = = Af= Here Loop Gain: The product of open loop gain and the feedback factor is called loop gain.
    [Show full text]
  • Unit I Microwave Transmission Lines
    UNIT I MICROWAVE TRANSMISSION LINES INTRODUCTION Microwaves are electromagnetic waves with wavelengths ranging from 1 mm to 1 m, or frequencies between 300 MHz and 300 GHz. Apparatus and techniques may be described qualitatively as "microwave" when the wavelengths of signals are roughly the same as the dimensions of the equipment, so that lumped-element circuit theory is inaccurate. As a consequence, practical microwave technique tends to move away from the discrete resistors, capacitors, and inductors used with lower frequency radio waves. Instead, distributed circuit elements and transmission-line theory are more useful methods for design, analysis. Open-wire and coaxial transmission lines give way to waveguides, and lumped-element tuned circuits are replaced by cavity resonators or resonant lines. Effects of reflection, polarization, scattering, diffraction, and atmospheric absorption usually associated with visible light are of practical significance in the study of microwave propagation. The same equations of electromagnetic theory apply at all frequencies. While the name may suggest a micrometer wavelength, it is better understood as indicating wavelengths very much smaller than those used in radio broadcasting. The boundaries between far infrared light, terahertz radiation, microwaves, and ultra-high-frequency radio waves are fairly arbitrary and are used variously between different fields of study. The term microwave generally refers to "alternating current signals with frequencies between 300 MHz (3×108 Hz) and 300 GHz (3×1011 Hz)."[1] Both IEC standard 60050 and IEEE standard 100 define "microwave" frequencies starting at 1 GHz (30 cm wavelength). Electromagnetic waves longer (lower frequency) than microwaves are called "radio waves". Electromagnetic radiation with shorter wavelengths may be called "millimeter waves", terahertz radiation or even T-rays.
    [Show full text]
  • Passband Data Transmission I Introduction in Digital Passband
    Passband Data Transmission I References Phase-shift keying Chapter 4.1-4.3, S. Haykin, Communication Systems, Wiley. J.1 Introduction In baseband pulse transmission, a data stream represented in the form of a discrete pulse-amplitude modulated (PAM) signal is transmitted over a low- pass channel. In digital passband transmission, the incoming data stream is modulated onto a carrier with fixed frequency and then transmitted over a band-pass channel. J.2 1 Passband digital transmission allows more efficient use of the allocated RF bandwidth, and flexibility in accommodating different baseband signal formats. Example Mobile Telephone Systems GSM: GMSK modulation is used (a variation of FSK) IS-54: π/4-DQPSK modulation is used (a variation of PSK) J.3 The modulation process making the transmission possible involves switching (keying) the amplitude, frequency, or phase of a sinusoidal carrier in accordance with the incoming data. There are three basic signaling schemes: Amplitude-shift keying (ASK) Frequency-shift keying (FSK) Phase-shift keying (PSK) J.4 2 ASK PSK FSK J.5 Unlike ASK signals, both PSK and FSK signals have a constant envelope. PSK and FSK are preferred to ASK signals for passband data transmission over nonlinear channel (amplitude nonlinearities) such as micorwave link and satellite channels. J.6 3 Classification of digital modulation techniques Coherent and Noncoherent Digital modulation techniques are classified into coherent and noncoherent techniques, depending on whether the receiver is equipped with a phase- recovery circuit or not. The phase-recovery circuit ensures that the local oscillator in the receiver is synchronized to the incoming carrier wave (in both frequency and phase).
    [Show full text]
  • Wave Guides & Resonators
    UNIT I WAVEGUIDES & RESONATORS INTRODUCTION Microwaves are electromagnetic waves with wavelengths ranging from 1 mm to 1 m, or frequencies between 300 MHz and 300 GHz. Apparatus and techniques may be described qualitatively as "microwave" when the wavelengths of signals are roughly the same as the dimensions of the equipment, so that lumped-element circuit theory is inaccurate. As a consequence, practical microwave technique tends to move away from the discrete resistors, capacitors, and inductors used with lower frequency radio waves. Instead, distributed circuit elements and transmission-line theory are more useful methods for design, analysis. Open-wire and coaxial transmission lines give way to waveguides, and lumped-element tuned circuits are replaced by cavity resonators or resonant lines. Effects of reflection, polarization, scattering, diffraction, and atmospheric absorption usually associated with visible light are of practical significance in the study of microwave propagation. The same equations of electromagnetic theory apply at all frequencies. While the name may suggest a micrometer wavelength, it is better understood as indicating wavelengths very much smaller than those used in radio broadcasting. The boundaries between far infrared light, terahertz radiation, microwaves, and ultra-high-frequency radio waves are fairly arbitrary and are used variously between different fields of study. The term microwave generally refers to "alternating current signals with frequencies between 300 MHz (3×108 Hz) and 300 GHz (3×1011 Hz)."[1] Both IEC standard 60050 and IEEE standard 100 define "microwave" frequencies starting at 1 GHz (30 cm wavelength). Electromagnetic waves longer (lower frequency) than microwaves are called "radio waves". Electromagnetic radiation with shorter wavelengths may be called "millimeter waves", terahertz Page 1 radiation or even T-rays.
    [Show full text]
  • Electronic Filters Design Tutorial - 3
    Electronic filters design tutorial - 3 High pass, low pass and notch passive filters In the first and second part of this tutorial we visited the band pass filters, with lumped and distributed elements. In this third part we will discuss about low-pass, high-pass and notch filters. The approach will be without mathematics, the goal will be to introduce readers to a physical knowledge of filters. People interested in a mathematical analysis will find in the appendix some books on the topic. Fig.2 ∗ The constant K low-pass filter: it was invented in 1922 by George Campbell and the Running the simulation we can see the response meaning of constant K is the expression: of the filter in fig.3 2 ZL* ZC = K = R ZL and ZC are the impedances of inductors and capacitors in the filter, while R is the terminating impedance. A look at fig.1 will be clarifying. Fig.3 It is clear that the sharpness of the response increase as the order of the filter increase. The ripple near the edge of the cutoff moves from Fig 1 monotonic in 3 rd order to ringing of about 1.7 dB for the 9 th order. This due to the mismatch of the The two filter configurations, at T and π are various sections that are connected to a 50 Ω displayed, all the reactance are 50 Ω and the impedance at the edges of the filter and filter cells are all equal. In practice the two series connected to reactive impedances between cells.
    [Show full text]
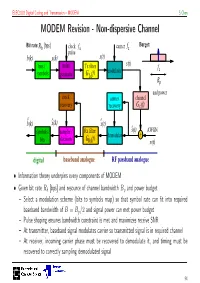
  • MODEM Revision
    ELEC3203 Digital Coding and Transmission – MODEM S Chen MODEM Revision - Non-dispersive Channel Burget: Bit rate:Rb [bps] clock fs carrier fc pulse b(k) x(k) x(t) bits / pulse Tx filter s(t) modulator fc symbols generator GTx (f) Bp and power clock carrier channel recovery recovery G c (f) b(k)^ x(k)^ x(t)^ symbols / sampler / Rx filter s(t)^ AWGN demodulat + bits decision GRx (f) n(t) digital baseband analogue RF passband analogue • Information theory underpins every components of MODEM • Given bit rate Rb [bps] and resource of channel bandwidth Bp and power budget – Select a modulation scheme (bits to symbols map) so that symbol rate can fit into required baseband bandwidth of B = Bp/2 and signal power can met power budget – Pulse shaping ensures bandwidth constraint is met and maximizes receive SNR – At transmitter, baseband signal modulates carrier so transmitted signal is in required channel – At receiver, incoming carrier phase must be recovered to demodulate it, and timing must be recovered to correctly sampling demodulated signal 94 ELEC3203 Digital Coding and Transmission – MODEM S Chen MODEM Revision - Dispersive Channel • For dispersive channel, equaliser at receiver aims to make combined channel/equaliser a Nyquist system again + = bandwidth bandwidth channel equaliser combined – Design of equaliser is a trade off between eliminating ISI and not enhancing noise too much • Generic framework of adaptive equalisation with training and decision-directed modes n[k] x[k] y[k] f[k] x[k−k^ ] Σ equaliser decision d channel circuit − Σ
    [Show full text]