DOCSLIB.ORG

Passband Data Transmission I Introduction in Digital Passband

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Passband Data Transmission I Introduction in Digital Passband Passband Data Transmission I References Phase-shift keying Chapter 4.1-4.3, S. Haykin, Communication Systems, Wiley. J.1 Introduction In baseband pulse transmission, a data stream represented in the form of a discrete pulse-amplitude modulated (PAM) signal is transmitted over a low- pass channel. In digital passband transmission, the incoming data stream is modulated onto a carrier with fixed frequency and then transmitted over a band-pass channel. J.2 1 Passband digital transmission allows more efficient use of the allocated RF bandwidth, and flexibility in accommodating different baseband signal formats. Example Mobile Telephone Systems GSM: GMSK modulation is used (a variation of FSK) IS-54: π/4-DQPSK modulation is used (a variation of PSK) J.3 The modulation process making the transmission possible involves switching (keying) the amplitude, frequency, or phase of a sinusoidal carrier in accordance with the incoming data. There are three basic signaling schemes: Amplitude-shift keying (ASK) Frequency-shift keying (FSK) Phase-shift keying (PSK) J.4 2 ASK PSK FSK J.5 Unlike ASK signals, both PSK and FSK signals have a constant envelope. PSK and FSK are preferred to ASK signals for passband data transmission over nonlinear channel (amplitude nonlinearities) such as micorwave link and satellite channels. J.6 3 Classification of digital modulation techniques Coherent and Noncoherent Digital modulation techniques are classified into coherent and noncoherent techniques, depending on whether the receiver is equipped with a phase- recovery circuit or not. The phase-recovery circuit ensures that the local oscillator in the receiver is synchronized to the incoming carrier wave (in both frequency and phase). J.7 Phase Recovery (Carrier Synchronization) Two ways in which a local oscillator can be synchronized with an incoming carrier wave transmit a pilot carrier use a carrier-recovery circuit such as a phase-locked loop (PPL) J.8 4 M-ary signaling In an M-ary signaling scheme, there are M possible signals during each signaling interval of duration T. Usually, n M = 2 and T = nTb where Tb is the bit duration. In passband transmission, we have M-ary ASK, M-ary PSK, and M-ary FSK digital modulation schemes. We can also combine different methods: M-ary amplitude-phase keying (APK) M-ary quadrature-amplitude modulation (QAM) In baseband transmission, we have M-ary PAM J.9 M-ary signaling schemes are preferred over binary signaling schemes for transmitting digital information over band-pass channels when the requirement is to conserve bandwidth at the expense of increased power. The use of M-ary signaling enables a reduction in transmission bandwidth by the factor n = log2 M over binary signaling. J.10 5 Coherent PSK The functional model of passband data transmission system is Signal Signal si si (t) x(t) x mi transmission Modulator Channel Detector transmission encoder decoder mˆ Carrier signal • mi is a sequence of symbol emitted from a message source. • The channel is linear, with a bandwidth that is wide enough to transmit the modulated signal and the channel noise is Gaussian distributed with zero mean and power spectral density No / 2. J.11 The following parameters are considered for a signaling scheme: Probability of error A major goal of passband data transmission systems is the optimum design of the receiver so as to minimize the average probability of symbol error in the presence of additive white Gaussian noise (AWGN) J.12 6 Power spectra Use to determine the signal bandwidth and co-channel interference in multiplexed systems. In practice, the signalings are linear operation, therefore, it is sufficient to evaluate the baseband power spectral density. Bandwidth Efficiency R Bandwidth efficiency ρ = b bits/s/Hz B where Rb is the data rate and B is the used channel bandwidth. J.13 In a coherent binary PSK system, the pair of signals s1 (t) and s2 (t) used to represent binary symbols 1 and 0, respectively, is defined by 2Eb s1 (t) = cos(2πfct) Tb 2Eb 2Eb s2 (t) = cos(2πfct +π ) = − cos(2πfct) Tb Tb where 0 ≤ t ≤ Tb , and Eb is the transmitted signal energy per bit. J.14 7 For example, T T b 2 2Eb b 2 2Eb Tb E = []s1 (t) dt = cos (2πfct)dt = ⋅ = Eb ∫0 ∫0 Tb Tb 2 To ensure that each transmitted bit contains an integral number of cycles of the carrier wave, the carrier frequency fc is chosen equal to n /Tb for some fixed integer n. J.15 The transmitted signal can be written as s1 (t) = Ebφ(t) and s2 (t) = − Ebφ(t) 2 where φ(t) = cos(2πfct) 0 ≤ t < Tb Tb J.16 8 Generation of coherent binary PSK signals To generate a binary PSK signal, we have to represent the input binary sequence in polar form with symbols 1 and 0 represented by constant amplitude levels of + Eb and − Eb , respectively. Signal si (t) 10101 si Product transmission Modulator encoder 2 φ(t) = cos(2πfct) Tb J.17 • This signal transmission encoder is performed by a polar nonreturn-to-zero (NRZ) encoder. + Eb input symbol is 1 si = − Eb input symbol is 0 • The carrier frequency fc = n /Tb where n is a fixed integer. 2Eb s1 (t) = cos(2πfct) if si = Eb Tb si (t) = 2Eb s2 (t) = − cos(2πfct) if si = − Eb Tb J.18 9 Detection of coherent binary PSK signals To detect the original binary sequence of 1s and 0s, we apply the noisy PSK signal to a correlator. The correlator output is compared with a threshold of zero volts. Tb x1 Decision 1 if x1 > 0 x(t) X ∫0 device 0 if x1 < 0 φ(t) 0 Correlator J.19 Example: If the transmitted symbol is 1, 2Eb x(t) = cos(2πfct) Tb and the correlator output is Tb x1 = x(t)φ(t)dt ∫0 T b 2Eb 2 = cos(2πfct)⋅ cos(2πfct)dt ∫0 Tb Tb T 2 b 2 = Eb ⋅ cos (2πfct)dt ∫0 Tb = Eb Similarly, If the transmitted symbol is 0, x1 = − Eb . J.20 10 Error probability of binary PSK We can represent a coherent binary system with a signal constellation consisting of two message points. • The coordinates of the message points are all the possible correlator output under a noiseless condition. • The coordinates for BPSK are Eb and − Eb . Decision boundary φ(t) − Eb Eb J.21 There are two possible kinds of erroneous decision: • Signal s2 (t) is transmitted, but the noise is such that the received signal point inside region with x1 > 0 and so the receiver decides in favor of signal s1 (t). • Signal s1 (t) is transmitted, but the noise is such that the received signal point inside region with x1 < 0 and so the receiver decides in favor of signal s2 (t). Tb x1 Decision 1 if x1 > 0 X ∫0 device < si (t) + w(t) 0 if x1 0 φ(t) 0 J.22 11 For the first case, the observable element x1 is related to the received signal x(t) by Tb x1 = x(t)φ(t)dt ∫0 Tb = []si (t) + w(t) φ(t)dt ∫0 Tb = − Eb + w(t)φ(t)dt ∫0 x1 is a Gaussian process with mean x1 : xi = E[xi ] Tb = E[− Eb + w(t)φ(t)dt] ∫0 = − Eb J.23 and variance σ : 2 2 σ = E[(xi − xi ) ] 2 Tb = E w(t)φ(t)dt ∫0 TTbb = E w(t)w(u)φ(t)φ(u)dtdu ∫∫00 TTbb = E[w(t)w(u)]φ(t)φ(u)dtdu ∫∫00 TTbbN = o δ (t − u)φ(t)φ(u)dtdu ∫∫00 2 N Tb = o φ 2 (t)dt 2 ∫0 N = o 2 J.24 12 Therefore, the conditional probability density function of x1, given that symbol 0 was transmitted is 2 1 (x1 − x1 ) f (x1 | 0) = exp− 2 2πσ 2σ 2 1 (x1 + Eb ) = exp− πNo No J.25 and the probability of error is ∞ p10 = f (x1 | 0)dx1 ∫0 2 ∞ 1 (x1 + Eb ) = exp− dx1 ∫0 πNo No 1 Putting z = (x + Eb ), we have No ∞ 1 2 p10 = exp[]− z dz π ∫ Eb / No 0 1 E 2 ∞ = erfc b erfc(u) = exp(−z 2 )dz π ∫ 2 No u J.26 13 Similarly, the error of the second kind 1 E b p01 = p10 = erfc and hence 2 No 1 E b pe = erfc 2 No J.27 Quadriphase-shift keying (QPSK) QPSK has twice the bandwith efficiency of BPSK, since 2 bits are transmitted in a single modulation symbol. The data input dk (t) is devided into an in- phase stream d I (t), and a quadrature stream dQ (t). J.28 14 1 0 0 1 dk (t) t 1 0 dI (t) t 0 1 dQ (t) t J.29 The phase of the carrier takes on one of four equally spaced values, such as π/4, 3π/4, 5π/4, and 7π/4. 2E cos[2πfct + (2i −1)π / 4] 0 ≤ t ≤ T si (t) = T 0 elsewhere where i =1,2,3,4. E is the transmitted signal energy per symbol; T is the symbol duration; fc = n /T ; (Note : T = 2Tb ) J.30 15 Each possible value of the phase corresponds to a unique dibit. For example, 10 for i=1, 00 for i=2, 01 for i=3 and 11 for i=4. (only a single bit is change from one dibit to the next) J.31 The transmitted signal can be written as 2E s (t) = cos[2πf t + (2i −1)π / 4] i T c 2E = cos[2πf t]cos[(2i −1)π / 4] T c 2E − sin[2πf t]sin[(2i −1)π / 4] T c = si1φ1(t) + si2φ2 (t) where 2 2 φ (t) = cos[2πf t]; φ (t) = sin[2πf t] 1 T c 2 T c J.32 16 Input dibit Phase of QPSK si1 si2 10 π/4 E / 2 − E / 2 00 3π/4 − E / 2 − E / 2 01 5π/4 − E / 2 E / 2 11 7π/4 E / 2 E / 2 J.33 J.34 17 The constellation of QPSK is φ2 (t) (00) E / 2 (10) E / 2 φ1(t) − E / 2 (11) (01) − E / 2 J.35 Generation of coherent QPSK signals The incoming binary data sequence is first transformed into polar form by a nonreturn-to-zero level encoder.
Load more

Recommended publications
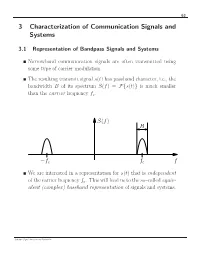
  • 3 Characterization of Communication Signals and Systems
    63 3 Characterization of Communication Signals and Systems 3.1 Representation of Bandpass Signals and Systems Narrowband communication signals are often transmitted using some type of carrier modulation. The resulting transmit signal s(t) has passband character, i.e., the bandwidth B of its spectrum S(f) = s(t) is much smaller F{ } than the carrier frequency fc. S(f) B f f f − c c We are interested in a representation for s(t) that is independent of the carrier frequency fc. This will lead us to the so–called equiv- alent (complex) baseband representation of signals and systems. Schober: Signal Detection and Estimation 64 3.1.1 Equivalent Complex Baseband Representation of Band- pass Signals Given: Real–valued bandpass signal s(t) with spectrum S(f) = s(t) F{ } Analytic Signal s+(t) In our quest to find the equivalent baseband representation of s(t), we first suppress all negative frequencies in S(f), since S(f) = S( f) is valid. − The spectrum S+(f) of the resulting so–called analytic signal s+(t) is defined as S (f) = s (t) =2 u(f)S(f), + F{ + } where u(f) is the unit step function 0, f < 0 u(f) = 1/2, f =0 . 1, f > 0 u(f) 1 1/2 f Schober: Signal Detection and Estimation 65 The analytic signal can be expressed as 1 s+(t) = − S+(f) F 1{ } = − 2 u(f)S(f) F 1{ } 1 = − 2 u(f) − S(f) F { } ∗ F { } 1 The inverse Fourier transform of − 2 u(f) is given by F { } 1 j − 2 u(f) = δ(t) + .
    [Show full text]
  • 2 the Wireless Channel
    CHAPTER 2 The wireless channel A good understanding of the wireless channel, its key physical parameters and the modeling issues, lays the foundation for the rest of the book. This is the goal of this chapter. A defining characteristic of the mobile wireless channel is the variations of the channel strength over time and over frequency. The variations can be roughly divided into two types (Figure 2.1): • Large-scale fading, due to path loss of signal as a function of distance and shadowing by large objects such as buildings and hills. This occurs as the mobile moves through a distance of the order of the cell size, and is typically frequency independent. • Small-scale fading, due to the constructive and destructive interference of the multiple signal paths between the transmitter and receiver. This occurs at the spatialscaleoftheorderofthecarrierwavelength,andisfrequencydependent. We will talk about both types of fading in this chapter, but with more emphasis on the latter. Large-scale fading is more relevant to issues such as cell-site planning. Small-scale multipath fading is more relevant to the design of reliable and efficient communication systems – the focus of this book. We start with the physical modeling of the wireless channel in terms of elec- tromagnetic waves. We then derive an input/output linear time-varying model for the channel, and define some important physical parameters. Finally, we introduce a few statistical models of the channel variation over time and over frequency. 2.1 Physical modeling for wireless channels Wireless channels operate through electromagnetic radiation from the trans- mitter to the receiver.
    [Show full text]
  • The Future of Passive Multiplexing & Multiplexing Beyond
    The Future of Passive Multiplexing & Multiplexing Beyond 10G From 1G to 10G was easy But Beyond 10G? 1G CWDM/DWDM 10G CWDM/DWDM 25G 40G Dark Fiber Passive Multiplexer 100G ? 400G Ingredients for Multiplexing 1) Dark Fiber 2) Multiplexers 3) Light : Transceivers Ingredients for Multiplexing 1) Dark Fiber 2 Multiplexer 3 Light + Transceiver Dark Fiber Attenuation → 0 km → → 40 km → → 80 km → Dispersion → 0 km → → 40 km → → 80 km → Dark Fiber Dispersion @1G DWDM max 200km → 0 km → → 40 km → → 80 km → @10G DWDM max 80km → 0 km → → 40 km → → 80 km → @25G DWDM max 15km → 0 km → → 40 km → → 80 km → Dark Fiber Attenuation → 80 km → 1310nm Window 1550nm/DWDM Dispersion → 80 km → Ingredients for Multiplexing 1 Dark FiBer 2) Multiplexers 3 Light + Transceiver Passive Mux Multiplexers 2 types • Cascaded TFF • AWG 95% of all Communication -Larger Multiplexers such as 40Ch/96Ch Multiplexers TFF: Thin film filter • Metal or glass tuBes 2cm*4mm • 3 fiBers: com / color / reflect • Each tuBe has 0.3dB loss • 95% of Muxes & OADM Multiplexers ABS casing Multiplexers AWG: arrayed wave grading -Larger muxes such as 40Ch/96Ch -Lower loss -Insertion loss 40ch = 3.0dB DWDM33 Transmission Window AWG Gaussian Fit Attenuation DWDM33 Low attenuation Small passband Reference passBand DWDM33 Isolation Flat Top Higher attenuation Wide passband DWDM light ALL TFF is Flat top Transmission Wave Types Flat Top: OK DWDM 10G Coherent 100G Gaussian Fit not OK DWDM PAM4 Ingredients for Multiplexing 1 Dark FiBer 2 Multiplexer 3) Light: Transceivers ITU Grids LWDM DWDM CWDM Attenuation
    [Show full text]
  • Performance Evaluation of Power-Line Communication Systems for LIN-Bus Based Data Transmission
    electronics Article Performance Evaluation of Power-Line Communication Systems for LIN-Bus Based Data Transmission Martin Brandl * and Karlheinz Kellner Department of Integrated Sensor Systems, Danube University, 3500 Krems, Austria; [email protected] * Correspondence: [email protected]; Tel.: +43-2732-893-2790 Abstract: Powerline communication (PLC) is a versatile method that uses existing infrastructure such as power cables for data transmission. This makes PLC an alternative and cost-effective technology for the transmission of sensor and actuator data by making dual use of the power line and avoiding the need for other communication solutions; such as wireless radio frequency communication. A PLC modem using DSSS (direct sequence spread spectrum) for reliable LIN-bus based data transmission has been developed for automotive applications. Due to the almost complete system implementation in a low power microcontroller; the component cost could be radically reduced which is a necessary requirement for automotive applications. For performance evaluation the DSSS modem was compared to two commercial PLC systems. The DSSS and one of the commercial PLC systems were designed as a direct conversion receiver; the other commercial module uses a superheterodyne architecture. The performance of the systems was tested under the influence of narrowband interference and additive Gaussian noise added to the transmission channel. It was found that the performance of the DSSS modem against singleton interference is better than that of commercial PLC transceivers by at least the processing gain. The performance of the DSSS modem was at least 6 dB better than the other modules tested under the influence of the additive white Gaussian noise on the transmission channel at data rates of 19.2 kB/s.
    [Show full text]
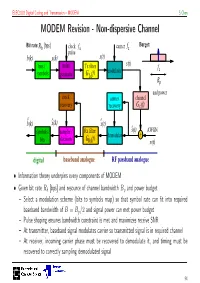
  • MODEM Revision
    ELEC3203 Digital Coding and Transmission – MODEM S Chen MODEM Revision - Non-dispersive Channel Burget: Bit rate:Rb [bps] clock fs carrier fc pulse b(k) x(k) x(t) bits / pulse Tx filter s(t) modulator fc symbols generator GTx (f) Bp and power clock carrier channel recovery recovery G c (f) b(k)^ x(k)^ x(t)^ symbols / sampler / Rx filter s(t)^ AWGN demodulat + bits decision GRx (f) n(t) digital baseband analogue RF passband analogue • Information theory underpins every components of MODEM • Given bit rate Rb [bps] and resource of channel bandwidth Bp and power budget – Select a modulation scheme (bits to symbols map) so that symbol rate can fit into required baseband bandwidth of B = Bp/2 and signal power can met power budget – Pulse shaping ensures bandwidth constraint is met and maximizes receive SNR – At transmitter, baseband signal modulates carrier so transmitted signal is in required channel – At receiver, incoming carrier phase must be recovered to demodulate it, and timing must be recovered to correctly sampling demodulated signal 94 ELEC3203 Digital Coding and Transmission – MODEM S Chen MODEM Revision - Dispersive Channel • For dispersive channel, equaliser at receiver aims to make combined channel/equaliser a Nyquist system again + = bandwidth bandwidth channel equaliser combined – Design of equaliser is a trade off between eliminating ISI and not enhancing noise too much • Generic framework of adaptive equalisation with training and decision-directed modes n[k] x[k] y[k] f[k] x[k−k^ ] Σ equaliser decision d channel circuit − Σ
    [Show full text]
  • Analysis of the PAPR Behavior of the OFDM Passband Signal
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 19 December 2019 doi:10.20944/preprints201912.0255.v1 Article Analysis of the PAPR Behavior of the OFDM Passband Signal Frank Andrés Eras 0000-0002-7844-5670, Italo Alexander Carreño, Thomas Borja, Diego Javier Reinoso* 0000-0003-0854-1250, Luis Felipe Urquiza 0000-0002-6405-2067, Martha Cecilia Paredes 0000-0001-5789-4568 Departamento de Electrónica, Telecomunicaciones y Redes de Información, Escuela Politécnica Nacional * Correspondence: [email protected] 1 Abstract: Orthogonal Frequency Division Multiplexing (OFDM) is a technique widely used in today’s 2 wireless communication systems due to its ability to combat the effects of multi-path in the signal. 3 However, one of the main limitations of the use of OFDM is its high Peak-to-Average Power Ratio 4 (PAPR), which reduces the efficiency of the OFDM system. The effects of PAPR can produce both 5 out-of-band and in-band radiation, which degrades the signal by increasing the bit error rate (BER), 6 this occurs in both baseband and bandpass sginals. In this document the effect of the PAPR in a 7 OFDM passband signal is analyzed considering the implementation of a High Power Amplifier (HPA) 8 and the Simple Amplitude Predistortion-Orthogonal Pilot Sequences (OPS-SAP) scheme to reduce 9 the PAPR. 10 Keywords: OFDM; PAPR; passband; IEEE 802.11p 11 1. Introduction 12 For some years, many wireless communication systems have based the transmission of 13 information on the Orthogonal Frequency Division Multiplexing (OFDM) scheme, which is used 14 in standards such as Long-Term Evolution (LTE), Wireless Local Area Networks (WLAN), Digital 15 Video Broadcasting (DVB-T), among others.
    [Show full text]
  • Quantum Key Distribution for 10 Gb/S Dense Wavelength Division Multiplexing Networks K
    Quantum key distribution for 10 Gb/s dense wavelength division multiplexing networks K. A. Patel,1,2 J. F. Dynes,1 M. Lucamarini,1 I. Choi,1 A. W. Sharpe,1 Z. L. Yuan,1 R. V. Penty2 and A. J. Shields1 1Toshiba Research Europe Limited, Cambridge Research Laboratory, 208 Cambridge Science Park, Milton Road, Cambridge, CB4 0GZ, United Kingdom 2Cambridge University Engineering Department, 9 J J Thomson Avenue, Cambridge, CB3 0FA, United Kingdom Abstract: We demonstrate quantum key distribution (QKD) with bidirectional 10 Gb/s classical data channels in a single fiber using dense wavelength division multiplexing. Record secure key rates of 2.38 Mbps and fiber distances up to 70 km are achieved. Data channels are simultaneously monitored for error-free operation. The robustness of QKD is further demonstrated with a secure key rate of 445 kbps over 25 km, obtained in the presence of data lasers launching conventional 0 dBm power. We discuss the fundamental limit for the QKD performance in the multiplexing environment. 1 Quantum key distribution (QKD)1 is revolutionizing the way of distributing secret cryptographic keys for information protection. Unlike its classical counterparts, it allows secure transmission of information with quantifiable security2-4 and detection of an eavesdropper. After numerous experiments in the laboratory4-7 as well as in field,8,9 the technology has matured for deployment on dark fiber with secure key rates exceeding 1 Mb/s. Nevertheless, for wider adoption, QKD must adapt to existing fiber infrastructures, which are populated with classical data communications. Quantum and classical data signals can be combined onto a single fiber using wavelength division multiplexing.
    [Show full text]
  • Fundamentals of Spread-Spectrum Techniques
    RGHEFF CH003.tex 13/6/2007 17: 33 Page 153 3 Fundamentals of spread-spectrum techniques In this chapter we consider the spread-spectrum transmission schemes that demand channel bandwidth much greater than is required by the Nyquist sampling theorem. You will recall from Chapter 2 that the minimum bandpass bandwidth required for data transmission through an ideal channel is equal to the data symbol rate.You will also recall that wideband reception allows a large amount of input noise power to the detector and thus degrades the quality of the detected data. Therefore, the receivers for spread-spectrum schemes have to convert the received wideband signals back to their original narrowband waveforms before detection. This process generates a certain amount of processing gain that can be used to combat radio jamming and interference. We will describe and discuss in detail the properties and methods of generation of the functions used in creating wide spectrum signals. Finally, we consider the multiple access properties of the spread-spectrum systems and outline the analytical model for evaluating the system performance. 3.1 Historical background There was intensive use of communications warfare during World War II. This technique outlined the ability to intercept and interfere with hostile communications. Consequently, this procedure stimulated a great deal of interest which led to the development of secure communications systems and work in this field was carried out on two fronts. Firstly, development in communication theory initiated encryption schemes (Shannon, 1949) to provide certain information protection. Secondly, work was initiated to harness the devel- opment of a new technology.
    [Show full text]
  • Quadrature Amplitude Modulation (QAM)
    Quadrature Amplitude Modulation (QAM) PAM signals occupy twice the bandwidth required for the baseband Transmit two PAM signals using carriers of the same frequency but in phase and quadrature Demodulation: QAM Transmitter Implementation QAM is widely used method for transmitting digital data over bandpass channels A basic QAM transmitter Inphase component Pulse a Impulse a*(t) a(t) n Shaping Modulator + d Map to Filter sin w t n Serial to c Constellation g (t) s(t) Parallel T Point * Pulse 1 Impulse b (t) b(t) Shaping - J Modulator bn Filter quadrature component gT(t) cos wct Using complex notation = − = ℜ s(t) a(t)cos wct b(t)sin wct s(t) {s+ (t)} which is the preenvelope of QAM ∞ ∞ − = + − jwct = jwckT − jwc (t kT ) s+ (t) (ak jbk )gT (t kT )e s+ (t) (ck e )gT (t kT)e −∞ −∞ Complex Symbols Quadriphase-Shift Keying (QPSK) 4-QAM Transmitted signal is contained in the phase imaginary imaginary real real M-ary PSK QPSK is a special case of M-ary PSK, where the phase of the carrier takes on one of M possible values imaginary real Pulse Shaping Filters The real pulse shaping g (t) filter response T = jwct = + Let h(t) gT (t)e hI (t) jhQ (t) = hI (t) gT (t)cos wct = where hQ (t) gT (t)sin wct = − This filter is a bandpass H (w) GT (w wc ) filter with the frequency response Transmitted Sequences Modulated sequences before passband shaping ' = ℜ jwc kT = − ak {ck e } ak cos wc kT bk sin wc kT ' = ℑ jwc kT = + bk {ck e } ak sin wc kT bk cos wc kT Using these definitions ∞ = ℜ = ' − − ' − s(t) {s+ (t)} ak hI (t kT) bk hQ (t kT)
    [Show full text]
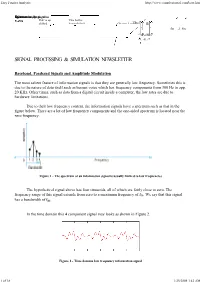
  • Easy Fourier Analysis
    Easy Fourier Analysis http://www.complextoreal.com/base.htm SpectrumDCInformationSignal term at 2w on csignal the positivenegative x-axis Half is up This half is shifted. down shifted. Charan Langton, The Carrier Editor fm = -1 fm = -9, fc-9,-9 -8, = -8, -8-7 -7 -9, -8, -7 SIGNAL PROCESSING & SIMULATION NEWSLETTER Baseband, Passband Signals and Amplitude Modulation The most salient feature of information signals is that they are generally low frequency. Sometimes this is due to the nature of data itself such as human voice which has frequency components from 300 Hz to app. 20 KHz. Other times, such as data from a digital circuit inside a computer, the low rates are due to hardware limitations. Due to their low frequency content, the information signals have a spectrum such as that in the figure below. There are a lot of low frequency components and the one-sided spectrum is located near the zero frequency. Figure 1 - The spectrum of an information signal is usually limited to low frequencies The hypothetical signal above has four sinusoids, all of which are fairly close to zero. The frequency range of this signal extends from zero to a maximum frequency of fm. We say that this signal has a bandwidth of fm. In the time domain this 4 component signal may looks as shown in Figure 2. Figure 2 - Time domain low frequency information signal 1 of 18 1/25/2008 3:42 AM Easy Fourier Analysis http://www.complextoreal.com/base.htm Now let’s modulate this signal, which means we are going to transfer it to a higher (usually much higher) frequency.
    [Show full text]
  • OFDM) and Advanced Signal Processing for Elastic Optical Networking in Accordance with Networking and Transmission Constraints
    Implementation of Orthogonal Frequency Division Multiplexing (OFDM) and Advanced Signal Processing for Elastic Optical Networking in Accordance with Networking and Transmission Constraints Item Type text; Electronic Dissertation Authors Johnson, Stanley Publisher The University of Arizona. Rights Copyright © is held by the author. Digital access to this material is made possible by the University Libraries, University of Arizona. Further transmission, reproduction or presentation (such as public display or performance) of protected items is prohibited except with permission of the author. Download date 09/10/2021 15:31:10 Link to Item http://hdl.handle.net/10150/612584 IMPLEMENTATION OF ORTHOGONAL FREQUENCY DIVISION MULTIPLEXING (OFDM) AND ADVANCED SIGNAL PROCESSING FOR ELASTIC OPTICAL NETWORKING IN ACCORDANCE WITH NETWORKING AND TRANSMISSION CONSTRAINTS by Stanley Johnson _____________________ Copyright © Stanley Johnson 2016 A Dissertation Submitted to the Faculty of the COLLEGE OF OPTICAL SCIENCES In Partial Fulfillment of the Requirements For the Degree of DOCTOR OF PHILOSOPHY In the Graduate College THE UNIVERSITY OF ARIZONA 2 0 1 6 2 THE UNIVERSITY OF ARIZONA GRADUATE COLLEGE As members of the Dissertation Committee, we certify that we have read the dissertation prepared by Stanley Johnson, titled Implementation of Orthogonal Frequency Division Multiplexing (OFDM) and Advanced Signal Processing for Elastic Optical Networking in Accordance with Networking and Transmission Constraints and recommend that it be accepted as fulfilling
    [Show full text]
  • Orthogonal Frequency Division Multiplex (OFDM) Tutorial 1
    Orthogonal Frequency Division Multiplex (OFDM) Tutorial 1 Intuitive Guide to Principles of Communications www.complextoreal.com Orthogonal Frequency Division Multiplexing (OFDM) Modulation - a mapping of the information on changes in the carrier phase, frequency or amplitude or combination. Multiplexing - method of sharing a bandwidth with other independent data channels. OFDM is a combination of modulation and multiplexing. Multiplexing generally refers to independent signals, those produced by different sources. So it is a question of how to share the spectrum with these users. In OFDM the question of multiplexing is applied to independent signals but these independent signals are a sub-set of the one main signal. In OFDM the signal itself is first split into independent channels, modulated by data and then re-multiplexed to create the OFDM carrier. OFDM is a special case of Frequency Division Multiplex (FDM). As an analogy, a FDM channel is like water flow out of a faucet, in contrast the OFDM signal is like a shower. In a faucet all water comes in one big stream and cannot be sub-divided. OFDM shower is made up of a lot of little streams. (a) (b) Fig. 1 – (a) A Regular-FDM single carrier – A whole bunch of water coming all in one stream. (b) Orthogonal-FDM – Same amount of water coming from a lot of small streams. Think about what the advantage might be of one over the other? One obvious one is that if I put my thumb over the faucet hole, I can stop the water flow but I cannot do the same for the shower.
    [Show full text]