COMP 551 – Applied Machine Learning Lecture 5: Generative Models for Linear Classification
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Descriptive Statistics (Part 2): Interpreting Study Results
Statistical Notes II Descriptive statistics (Part 2): Interpreting study results A Cook and A Sheikh he previous paper in this series looked at ‘baseline’. Investigations of treatment effects can be descriptive statistics, showing how to use and made in similar fashion by comparisons of disease T interpret fundamental measures such as the probability in treated and untreated patients. mean and standard deviation. Here we continue with descriptive statistics, looking at measures more The relative risk (RR), also sometimes known as specific to medical research. We start by defining the risk ratio, compares the risk of exposed and risk and odds, the two basic measures of disease unexposed subjects, while the odds ratio (OR) probability. Then we show how the effect of a disease compares odds. A relative risk or odds ratio greater risk factor, or a treatment, can be measured using the than one indicates an exposure to be harmful, while relative risk or the odds ratio. Finally we discuss the a value less than one indicates a protective effect. ‘number needed to treat’, a measure derived from the RR = 1.2 means exposed people are 20% more likely relative risk, which has gained popularity because of to be diseased, RR = 1.4 means 40% more likely. its clinical usefulness. Examples from the literature OR = 1.2 means that the odds of disease is 20% higher are used to illustrate important concepts. in exposed people. RISK AND ODDS Among workers at factory two (‘exposed’ workers) The probability of an individual becoming diseased the risk is 13 / 116 = 0.11, compared to an ‘unexposed’ is the risk. -

Teacher Guide 12.1 Gambling Page 1
TEACHER GUIDE 12.1 GAMBLING PAGE 1 Standard 12: The student will explain and evaluate the financial impact and consequences of gambling. Risky Business Priority Academic Student Skills Personal Financial Literacy Objective 12.1: Analyze the probabilities involved in winning at games of chance. Objective 12.2: Evaluate costs and benefits of gambling to Simone, Paula, and individuals and society (e.g., family budget; addictive behaviors; Randy meet in the library and the local and state economy). every afternoon to work on their homework. Here is what is going on. Ryan is flipping a coin, and he is not cheating. He has just flipped seven heads in a row. Is Ryan’s next flip more likely to be: Heads; Tails; or Heads and tails are equally likely. Paula says heads because the first seven were heads, so the next one will probably be heads too. Randy says tails. The first seven were heads, so the next one must be tails. Lesson Objectives Simone says that it could be either heads or tails Recognize gambling as a form of risk. because both are equally Calculate the probabilities of winning in games of chance. likely. Who is correct? Explore the potential benefits of gambling for society. Explore the potential costs of gambling for society. Evaluate the personal costs and benefits of gambling. © 2008. Oklahoma State Department of Education. All rights reserved. Teacher Guide 12.1 2 Personal Financial Literacy Vocabulary Dependent event: The outcome of one event affects the outcome of another, changing the TEACHING TIP probability of the second event. This lesson is based on risk. -

Odds: Gambling, Law and Strategy in the European Union Anastasios Kaburakis* and Ryan M Rodenberg†
63 Odds: Gambling, Law and Strategy in the European Union Anastasios Kaburakis* and Ryan M Rodenberg† Contemporary business law contributions argue that legal knowledge or ‘legal astuteness’ can lead to a sustainable competitive advantage.1 Past theses and treatises have led more academic research to endeavour the confluence between law and strategy.2 European scholars have engaged in the Proactive Law Movement, recently adopted and incorporated into policy by the European Commission.3 As such, the ‘many futures of legal strategy’ provide * Dr Anastasios Kaburakis is an assistant professor at the John Cook School of Business, Saint Louis University, teaching courses in strategic management, sports business and international comparative gaming law. He holds MS and PhD degrees from Indiana University-Bloomington and a law degree from Aristotle University in Thessaloniki, Greece. Prior to academia, he practised law in Greece and coached basketball at the professional club and national team level. He currently consults international sport federations, as well as gaming operators on regulatory matters and policy compliance strategies. † Dr Ryan Rodenberg is an assistant professor at Florida State University where he teaches sports law analytics. He earned his JD from the University of Washington-Seattle and PhD from Indiana University-Bloomington. Prior to academia, he worked at Octagon, Nike and the ATP World Tour. 1 See C Bagley, ‘What’s Law Got to Do With It?: Integrating Law and Strategy’ (2010) 47 American Business Law Journal 587; C -
3. Probability Theory
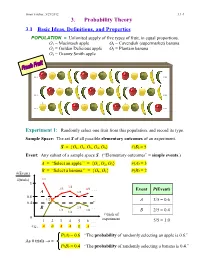
Ismor Fischer, 5/29/2012 3.1-1 3. Probability Theory 3.1 Basic Ideas, Definitions, and Properties POPULATION = Unlimited supply of five types of fruit, in equal proportions. O1 = Macintosh apple O4 = Cavendish (supermarket) banana O2 = Golden Delicious apple O5 = Plantain banana O3 = Granny Smith apple … … … … … … Experiment 1: Randomly select one fruit from this population, and record its type. Sample Space: The set S of all possible elementary outcomes of an experiment. S = {O1, O2, O3, O4, O5} #(S) = 5 Event: Any subset of a sample space S. (“Elementary outcomes” = simple events.) A = “Select an apple.” = {O1, O2, O3} #(A) = 3 B = “Select a banana.” = {O , O } #(B) = 2 #(Event) 4 5 #(trials) 1/1 1 3/4 2/3 4/6 . Event P(Event) A 3/5 0.6 1/2 A 3/5 = 0.6 0.4 B 2/5 . 1/3 2/6 1/4 B 2/5 = 0.4 # trials of 0 experiment 1 2 3 4 5 6 . 5/5 = 1.0 e.g., A B A A B A . P(A) = 0.6 “The probability of randomly selecting an apple is 0.6.” As # trials → ∞ P(B) = 0.4 “The probability of randomly selecting a banana is 0.4.” Ismor Fischer, 5/29/2012 3.1-2 General formulation may be facilitated with the use of a Venn diagram: Experiment ⇒ Sample Space: S = {O1, O2, …, Ok} #(S) = k A Om+1 Om+2 O2 O1 O3 Om+3 O 4 . Om . Ok Event A = {O1, O2, …, Om} ⊆ S #(A) = m ≤ k Definition: The probability of event A, denoted P(A), is the long-run relative frequency with which A is expected to occur, as the experiment is repeated indefinitely. -

Probability Cheatsheet V2.0 Thinking Conditionally Law of Total Probability (LOTP)
Probability Cheatsheet v2.0 Thinking Conditionally Law of Total Probability (LOTP) Let B1;B2;B3; :::Bn be a partition of the sample space (i.e., they are Compiled by William Chen (http://wzchen.com) and Joe Blitzstein, Independence disjoint and their union is the entire sample space). with contributions from Sebastian Chiu, Yuan Jiang, Yuqi Hou, and Independent Events A and B are independent if knowing whether P (A) = P (AjB )P (B ) + P (AjB )P (B ) + ··· + P (AjB )P (B ) Jessy Hwang. Material based on Joe Blitzstein's (@stat110) lectures 1 1 2 2 n n A occurred gives no information about whether B occurred. More (http://stat110.net) and Blitzstein/Hwang's Introduction to P (A) = P (A \ B1) + P (A \ B2) + ··· + P (A \ Bn) formally, A and B (which have nonzero probability) are independent if Probability textbook (http://bit.ly/introprobability). Licensed and only if one of the following equivalent statements holds: For LOTP with extra conditioning, just add in another event C! under CC BY-NC-SA 4.0. Please share comments, suggestions, and errors at http://github.com/wzchen/probability_cheatsheet. P (A \ B) = P (A)P (B) P (AjC) = P (AjB1;C)P (B1jC) + ··· + P (AjBn;C)P (BnjC) P (AjB) = P (A) P (AjC) = P (A \ B1jC) + P (A \ B2jC) + ··· + P (A \ BnjC) P (BjA) = P (B) Last Updated September 4, 2015 Special case of LOTP with B and Bc as partition: Conditional Independence A and B are conditionally independent P (A) = P (AjB)P (B) + P (AjBc)P (Bc) given C if P (A \ BjC) = P (AjC)P (BjC). -

Understanding Relative Risk, Odds Ratio, and Related Terms: As Simple As It Can Get Chittaranjan Andrade, MD
Understanding Relative Risk, Odds Ratio, and Related Terms: As Simple as It Can Get Chittaranjan Andrade, MD Each month in his online Introduction column, Dr Andrade Many research papers present findings as odds ratios (ORs) and considers theoretical and relative risks (RRs) as measures of effect size for categorical outcomes. practical ideas in clinical Whereas these and related terms have been well explained in many psychopharmacology articles,1–5 this article presents a version, with examples, that is meant with a view to update the knowledge and skills to be both simple and practical. Readers may note that the explanations of medical practitioners and examples provided apply mostly to randomized controlled trials who treat patients with (RCTs), cohort studies, and case-control studies. Nevertheless, similar psychiatric conditions. principles operate when these concepts are applied in epidemiologic Department of Psychopharmacology, National Institute research. Whereas the terms may be applied slightly differently in of Mental Health and Neurosciences, Bangalore, India different explanatory texts, the general principles are the same. ([email protected]). ABSTRACT Clinical Situation Risk, and related measures of effect size (for Consider a hypothetical RCT in which 76 depressed patients were categorical outcomes) such as relative risks and randomly assigned to receive either venlafaxine (n = 40) or placebo odds ratios, are frequently presented in research (n = 36) for 8 weeks. During the trial, new-onset sexual dysfunction articles. Not all readers know how these statistics was identified in 8 patients treated with venlafaxine and in 3 patients are derived and interpreted, nor are all readers treated with placebo. These results are presented in Table 1. -

Random Variables and Applications
Random Variables and Applications OPRE 6301 Random Variables. As noted earlier, variability is omnipresent in the busi- ness world. To model variability probabilistically, we need the concept of a random variable. A random variable is a numerically valued variable which takes on different values with given probabilities. Examples: The return on an investment in a one-year period The price of an equity The number of customers entering a store The sales volume of a store on a particular day The turnover rate at your organization next year 1 Types of Random Variables. Discrete Random Variable: — one that takes on a countable number of possible values, e.g., total of roll of two dice: 2, 3, ..., 12 • number of desktops sold: 0, 1, ... • customer count: 0, 1, ... • Continuous Random Variable: — one that takes on an uncountable number of possible values, e.g., interest rate: 3.25%, 6.125%, ... • task completion time: a nonnegative value • price of a stock: a nonnegative value • Basic Concept: Integer or rational numbers are discrete, while real numbers are continuous. 2 Probability Distributions. “Randomness” of a random variable is described by a probability distribution. Informally, the probability distribution specifies the probability or likelihood for a random variable to assume a particular value. Formally, let X be a random variable and let x be a possible value of X. Then, we have two cases. Discrete: the probability mass function of X specifies P (x) P (X = x) for all possible values of x. ≡ Continuous: the probability density function of X is a function f(x) that is such that f(x) h P (x < · ≈ X x + h) for small positive h. -

Medical Statistics PDF File 9
M249 Practical modern statistics Medical statistics About this module M249 Practical modern statistics uses the software packages IBM SPSS Statistics (SPSS Inc.) and WinBUGS, and other software. This software is provided as part of the module, and its use is covered in the Introduction to statistical modelling and in the four computer books associated with Books 1 to 4. This publication forms part of an Open University module. Details of this and other Open University modules can be obtained from the Student Registration and Enquiry Service, The Open University, PO Box 197, Milton Keynes MK7 6BJ, United Kingdom (tel. +44 (0)845 300 60 90; email [email protected]). Alternatively, you may visit the Open University website at www.open.ac.uk where you can learn more about the wide range of modules and packs offered at all levels by The Open University. To purchase a selection of Open University materials visit www.ouw.co.uk, or contact Open University Worldwide, Walton Hall, Milton Keynes MK7 6AA, United Kingdom for a brochure (tel. +44 (0)1908 858779; fax +44 (0)1908 858787; email [email protected]). Note to reader Mathematical/statistical content at the Open University is usually provided to students in printed books, with PDFs of the same online. This format ensures that mathematical notation is presented accurately and clearly. The PDF of this extract thus shows the content exactly as it would be seen by an Open University student. Please note that the PDF may contain references to other parts of the module and/or to software or audio-visual components of the module. -

Generalized Naive Bayes Classifiers
Generalized Naive Bayes Classifiers Kim Larsen Concord, California [email protected] ABSTRACT This paper presents a generalization of the Naive Bayes Clas- sifier. The method is called the Generalized Naive Bayes This paper presents a generalization of the Naive Bayes Clas- Classifier (GNBC) and extends the NBC by relaxing the sifier. The method is specifically designed for binary clas- assumption of conditional independence between the pre- sification problems commonly found in credit scoring and dictors. This reduces the bias in the estimated class prob- marketing applications. The Generalized Naive Bayes Clas- abilities and improves the fit, while greatly enhancing the sifier turns out to be a powerful tool for both exploratory descriptive value of the model. The generalization is done in and predictive analysis. It can generate accurate predictions a fully non-parametric fashion without putting any restric- through a flexible, non-parametric fitting procedure, while tions on the relationship between the independent variables being able to uncover hidden patterns in the data. In this and the dependent variable. This makes the GNBC much paper, the Generalized Naive Bayes Classifier and the orig- more flexible than traditional linear and non-linear regres- inal Bayes Classifier will be demonstrated. Also, important sion, and allows it to uncover hidden patterns in the data. ties to logistic regression, the Generalized Additive Model Moreover, the GNBC retains the additive structure of the (GAM), and Weight Of Evidence will be discussed. NBC which means that it does not suffer from the prob- lems of dimensionality that are common with other non- 1. INTRODUCTION parametric techniques. -

A Guide Odds
THE HOUSE ADVANTAGE A Guide to Understanding The Odds AMERICAN GAMING ASSOCIATION 1299 Pennsylvania Avenue, NW Suite 1175 Washington, DC 20004 202-552-2675 www.americangaming.org ©2011 American Gaming Association. All rights reserved. Whether you play slots, craps, blackjack, roulette or any other game in a casino, it is important to remember that games of chance are based on random outcomes and always favor the casino. These games of chance are a form of entertainment, at a price to you, the player. Casino gaming should not be considered a way to make money. This booklet provides information about the advantage the casino has in various games — also known as the “house advantage.” Beyond mathematical probabilities, it covers other factors a player should take into account, such as the amount wagered, length of time spent playing a game and, to a degree, the level of a player’s skill at certain games. Finally, the booklet discusses some of the common myths associated with gambling that should be understood before betting on any casino games. We encourage you to play responsibly by betting within your limits and by recognizing that over time the house will come out ahead. The American Gaming Association would like to thank Olaf Vancura, Ph.D. for the generous contribution of his time and expertise in the development of this brochure. 1 Understanding the Other Factors Behind House Advantage Winning and Losing Casino games are designed with a house While the house advantage is useful for advantage. Mathematically, the house advantage is understanding the casino’s expected win (or a a measure of how much the house expects to win, player’s expected loss) per bet, there are other expressed as a percentage of the player’s wager. -

Classification with Naive Bayes
Classification with Naive Bayes Benjamin Roth (Many thanks to Helmut Schmid for parts of the slides) Centrum fur¨ Informations- und Sprachverarbeitung Ludwig-Maximilian-Universit¨at Munchen¨ [email protected] Benjamin Roth (Many thanks to Helmut Schmid forClassification parts of the slides) with Naive (CIS) Bayes 1 / 50 Mathematical basics Benjamin Roth (Many thanks to Helmut Schmid forClassification parts of the slides) with Naive (CIS) Bayes 2 / 50 Random experiment Statistics is about the probability of events: Example: How likely is it to have six correct numbers in the lottery? Random experiment: Experiment (trial) with several possible outputs (throw of two dices) Outcome: Result of an experiment (3 eyes on dice 1 and 4 eyes on dice 2) Sample space Ω: Set of all possible outcomes Event: Subset of the sample space (7 eyes on two dices) Sample: Series of results in a repeated experiment Benjamin Roth (Many thanks to Helmut Schmid forClassification parts of the slides) with Naive (CIS) Bayes 3 / 50 Probability distribution Probability distribution: Function that assigns a value between 0 and 1 to each outcome, such that X p(o) = 1 o2Ω The probability of a event is the sum of the probabilities of the corresponding outcomes. Example: probability that the number of eyes when throwing a dice is an even number Benjamin Roth (Many thanks to Helmut Schmid forClassification parts of the slides) with Naive (CIS) Bayes 4 / 50 Conditional and a priori probability Conditional probability: Probability of an event A, if the event B is known: P(A \ B) P(AjB) = P(B) Example: Probability that the number of points in a dice is even if the number of points is greater than 3 A priori probability P(A): Probability of event A without knowing event B Benjamin Roth (Many thanks to Helmut Schmid forClassification parts of the slides) with Naive (CIS) Bayes 5 / 50 Random variables Random variable: Function that assigns a real number to each outcome. -

Section 8.1 - Distributions of Random Variables
c Kendra Kilmer March 22, 2010 Section 8.1 - Distributions of Random Variables Definition:A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could define the random variable X to represent the number of times we get tails. Example 2: Suppose we roll a die until a 5 is facing up. Then we could define the random variable Y to represent the number of times we rolled the die. Example 3: Suppose a flashlight is left on until the battery runs out. Then we could define the random variable Z to represent the amount of time that passed. Types of Random Variables 1. A finite discrete random variable is one which can only take on a limited number of values that can be listed. 2. An infinite discrete random variable is one which can take on an unlimited number of values that can be listed in some sort of sequence. 3. A continuous random variable is one which takes on any of the infinite number of values in some interval of real numbers. (i.e. usually measurements) Example 4: Referring to Example 1, find the probability distribution of the random variable X. 1 c Kendra Kilmer March 22, 2010 Example 5: The number of cars waiting in line at the beginning of 2-minute intervals at a certain bank was observed. The following data was collected: Number of cars 0 1 2 3 4 Frequency of occurence 2 2 16 8 2 Let X represent the number of cars observed waiting in line and find the probability distribution of X We use histograms to represent the probability distributions of random variables.