Model of MOSFET in Delphi
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Quantum Mechanics Electromotive Force
Quantum Mechanics_Electromotive force . Electromotive force, also called emf[1] (denoted and measured in volts), is the voltage developed by any source of electrical energy such as a batteryor dynamo.[2] The word "force" in this case is not used to mean mechanical force, measured in newtons, but a potential, or energy per unit of charge, measured involts. In electromagnetic induction, emf can be defined around a closed loop as the electromagnetic workthat would be transferred to a unit of charge if it travels once around that loop.[3] (While the charge travels around the loop, it can simultaneously lose the energy via resistance into thermal energy.) For a time-varying magnetic flux impinging a loop, theElectric potential scalar field is not defined due to circulating electric vector field, but nevertheless an emf does work that can be measured as a virtual electric potential around that loop.[4] In a two-terminal device (such as an electrochemical cell or electromagnetic generator), the emf can be measured as the open-circuit potential difference across the two terminals. The potential difference thus created drives current flow if an external circuit is attached to the source of emf. When current flows, however, the potential difference across the terminals is no longer equal to the emf, but will be smaller because of the voltage drop within the device due to its internal resistance. Devices that can provide emf includeelectrochemical cells, thermoelectric devices, solar cells and photodiodes, electrical generators,transformers, and even Van de Graaff generators.[4][5] In nature, emf is generated whenever magnetic field fluctuations occur through a surface. -

Chapter 4: Bonding in Solids and Electronic Properties
Chapter 4: Bonding in Solids and Electronic Properties Free electron theory Consider free electrons in a metal – an electron gas. •regards a metal as a box in which electrons are free to move. •assumes nuclei stay fixed on their lattice sites surrounded by core electrons, while the valence electrons move freely through the solid. •Ignoring the core electrons, one can treat the outer electrons with a quantum mechanical description. •Taking just one electron, the problem is reduced to a particle in a box. Electron is confined to a line of length a. Schrodinger equation 2 2 2 d d 2me E 2 (E V ) 2 2 2me dx dx Electron is not allowed outside the box, so the potential is ∞ outside the box. Energy is quantized, with quantum numbers n. 2 2 2 n2h2 h2 n n n In 1d: E In 3d: E a b c 2 8m a2 b2 c2 8mea e 1 2 2 2 2 Each set of quantum numbers n , n , h n n n a b a b c E 2 2 2 and nc will give rise to an energy level. 8me a b c •In three dimensions, there are multiple combination of energy levels that will give the same energy, whereas in one-dimension n and –n are equal in energy. 2 2 2 2 2 2 na/a nb/b nc/c na /a + nb /b + nc /c 6 6 6 108 The number of states with the 2 2 10 108 same energy is known as the degeneracy. 2 10 2 108 10 2 2 108 When dealing with a crystal with ~1020 atoms, it becomes difficult to work out all the possible combinations. -
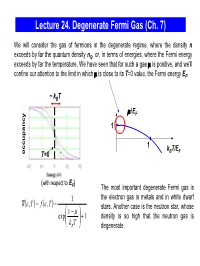
Lecture 24. Degenerate Fermi Gas (Ch
Lecture 24. Degenerate Fermi Gas (Ch. 7) We will consider the gas of fermions in the degenerate regime, where the density n exceeds by far the quantum density nQ, or, in terms of energies, where the Fermi energy exceeds by far the temperature. We have seen that for such a gas μ is positive, and we’ll confine our attention to the limit in which μ is close to its T=0 value, the Fermi energy EF. ~ kBT μ/EF 1 1 kBT/EF occupancy T=0 (with respect to E ) F The most important degenerate Fermi gas is 1 the electron gas in metals and in white dwarf nε()(),, T= f ε T = stars. Another case is the neutron star, whose ε⎛ − μ⎞ exp⎜ ⎟ +1 density is so high that the neutron gas is ⎝kB T⎠ degenerate. Degenerate Fermi Gas in Metals empty states ε We consider the mobile electrons in the conduction EF conduction band which can participate in the charge transport. The band energy is measured from the bottom of the conduction 0 band. When the metal atoms are brought together, valence their outer electrons break away and can move freely band through the solid. In good metals with the concentration ~ 1 electron/ion, the density of electrons in the electron states electron states conduction band n ~ 1 electron per (0.2 nm)3 ~ 1029 in an isolated in metal electrons/m3 . atom The electrons are prevented from escaping from the metal by the net Coulomb attraction to the positive ions; the energy required for an electron to escape (the work function) is typically a few eV. -

Chapter 13 Ideal Fermi
Chapter 13 Ideal Fermi gas The properties of an ideal Fermi gas are strongly determined by the Pauli principle. We shall consider the limit: k T µ,βµ 1, B � � which defines the degenerate Fermi gas. In this limit, the quantum mechanical nature of the system becomes especially important, and the system has little to do with the classical ideal gas. Since this chapter is devoted to fermions, we shall omit in the following the subscript ( ) that we used for the fermionic statistical quantities in the previous chapter. − 13.1 Equation of state Consider a gas ofN non-interacting fermions, e.g., electrons, whose one-particle wave- functionsϕ r(�r) are plane-waves. In this case, a complete set of quantum numbersr is given, for instance, by the three cartesian components of the wave vector �k and thez spin projectionm s of an electron: r (k , k , k , m ). ≡ x y z s Spin-independent Hamiltonians. We will consider only spin independent Hamiltonian operator of the type ˆ 3 H= �k ck† ck + d r V(r)c r†cr , �k � where thefirst and the second terms are respectively the kinetic and th potential energy. The summation over the statesr (whenever it has to be performed) can then be reduced to the summation over states with different wavevectork(p=¯hk): ... (2s + 1) ..., ⇒ r � �k where the summation over the spin quantum numberm s = s, s+1, . , s has been taken into account by the prefactor (2s + 1). − − 159 160 CHAPTER 13. IDEAL FERMI GAS Wavefunctions in a box. We as- sume that the electrons are in a vol- ume defined by a cube with sidesL x, Ly,L z and volumeV=L xLyLz. -

Thermoelectric Phenomena
Journal of Materials Education Vol. 36 (5-6): 175 - 186 (2014) THERMOELECTRIC PHENOMENA Witold Brostow a, Gregory Granowski a, Nathalie Hnatchuk a, Jeff Sharp b and John B. White a, b a Laboratory of Advanced Polymers & Optimized Materials (LAPOM), Department of Materials Science and Engineering and Department of Physics, University of North Texas, 3940 North Elm Street, Denton, TX 76207, USA; http://www.unt.edu/LAPOM/; [email protected], [email protected], [email protected]; [email protected] b Marlow Industries, Inc., 10451 Vista Park Road, Dallas, TX 75238-1645, USA; Jeffrey.Sharp@ii- vi.com ABSTRACT Potential usefulness of thermoelectric (TE) effects is hard to overestimate—while at the present time the uses of those effects are limited to niche applications. Possibly because of this situation, coverage of TE effects, TE materials and TE devices in instruction in Materials Science and Engineering is largely perfunctory and limited to discussions of thermocouples. We begin a series of review articles to remedy this situation. In the present article we discuss the Seebeck effect, the Peltier effect, and the role of these effects in semiconductor materials and in the electronics industry. The Seebeck effect allows creation of a voltage on the basis of the temperature difference. The twin Peltier effect allows cooling or heating when two materials are connected to an electric current. Potential consequences of these phenomena are staggering. If a dramatic improvement in thermoelectric cooling device efficiency were achieved, the resulting elimination of liquid coolants in refrigerators would stop one contribution to both global warming and destruction of the Earth's ozone layer. -

MOS Capacitors –Theoretical Exercise 3
Semiconductor Device Theory: MOS Capacitors –Theoretical Exercise 3 Dragica Vasileska and Gerhard Klimeck (ASU, Purdue) 1. For an MOS structure, find the charge per unit area in fast surface states ( Qs) as a function of the surface potential ϕs for the surface states density uniformly distributed in energy through- 11 -2 -1 out the forbidden gap with density Dst = 10 cm eV , located at the boundary between the oxide and semiconductor. Assume that the surface states with energies above the neutral level φ0 are acceptor type and that surface states with energies below the neutral level φ0 are donor type. Also assume that all surface states below the Fermi level are filled and that all surface states with energies above the Fermi level are empty (zero-temperature statistics for the sur- face states). The energy gap is Eg=1.12 eV, the neutral level φ0 is 0.3 eV above the valence 10 -3 band edge, the intrinsic carrier concentration is ni=1.5×10 cm , and the semiconductor dop- 15 -3 ing is NA=10 cm . Temperature equals T=300 K. 2. Express the capacitance of an MOS structure per unit area in the presence of uniformly dis- tributed fast surface states (as described in the previous problem) in terms of the oxide ca- pacitance Cox , per unit area. The semiconductor capacitance equals to Cs=-dQs/d ϕs (where Qs is the charge in the semiconductor and ϕs is the surface potential), and the surface states ca- pacitance is defined as Css =-dQst /d ϕs, where Qst is the charge in fast surface states per unit area. -

Sixfold Fermion Near the Fermi Level in Cubic Ptbi2 Abstract Contents
SciPost Phys. 10, 004 (2021) Sixfold fermion near the Fermi level in cubic PtBi2 Setti Thirupathaiah1, 2, Yevhen Kushnirenko1, Klaus Koepernik1, 3, Boy Roman Piening1, Bernd Büchner1, 3, Saicharan Aswartham1, Jeroen van den Brink1, 3, Sergey Borisenko1 and Ion Cosma Fulga1, 3? 1 IFW Dresden, Helmholtzstr. 20, 01069 Dresden, Germany 2 Condensed Matter Physics and Material Sciences Department, S. N. Bose National Centre for Basic Sciences, Kolkata, West Bengal-700106, India 3 Würzburg-Dresden Cluster of Excellence ct.qmat, Germany ? [email protected] Abstract We show that the cubic compound PtBi2 is a topological semimetal hosting a sixfold band touching point in close proximity to the Fermi level. Using angle-resolved photoemission spectroscopy, we map the band structure of the system, which is in good agreement with results from density functional theory. Further, by employing a low energy effective Hamiltonian valid close to the crossing point, we study the effect of a magnetic field on the sixfold fermion. The latter splits into a total of twenty Weyl cones for a Zeeman field oriented in the diagonal, (111) direction. Our results mark cubic PtBi2 as an ideal candidate to study the transport properties of gapless topological systems beyond Dirac and Weyl semimetals. Copyright S. Thirupathaiah et al. Received 17-06-2020 This work is licensed under the Creative Commons Accepted 03-12-2020 Check for Attribution 4.0 International License. Published 11-01-2021 updates Published by the SciPost Foundation. doi:10.21468/SciPostPhys.10.1.004 Contents 1 Introduction1 2 Band structure mapping2 2.1 Theory 2 2.2 Experiment4 3 Low energy model7 4 Conclusion 9 A Model parameters from ab-initio data 10 References 11 1 SciPost Phys. -

Quasi-Fermi Levels
6.772/SMA5111 - Compound Semiconductors Supplement 1 - Semiconductor Physics Review - Outline • The Fermi function and the Fermi level The occupancy of semiconductor energy levels • Effective density of states Conduction and valence band density of states 1. General 2. Parabolic bands • Quasi Fermi levels The concept and definition Examples of application 1. Uniform electric field on uniform sample 2. Forward biased p-n junction 3. Graded composition p-type heterostructure 4. Band edge gradients as effective forces for carrier drift Refs: R. F. Pierret, Semiconductor Fundamentals 2nd. Ed., (Vol. 1 of the Modular Series on Solid State Devices, Addison-Wesley, 1988); TK7871.85.P485; ISBN 0-201-12295-2. S. M. Sze, Physics of Semiconductor Devices (see course bibliography) Appendix C in Fonstad (handed out earlier; on course web site) C. G. Fonstad, 2/03 Supplement 1 - Slide 1 Fermi level and quasi-Fermi Levels - review of key points Fermi level: In thermal equilibrium the probability of finding an energy level at E occupied is given by the Fermi function, f(E): - f (E) =1 (1 +e[E E f ]/ kT ) where Ef is the Fermi energy, or level. In thermal equilibrium Ef is constant and not a function of position. The Fermi function has the following useful properties: - - ª [E E f ]/ kT - >> f (E) e for (E E f ) kT - ª - [E E f ]/ kT - << - f (E) 1 e for (E E f ) kT = = f (E f ) 1/2 for E E f These relationships tell us that the population of electrons decreases exponentially with energy at energies much more than kT above the Fermi level, and similarly that the population of holes (empty electron states) decreases exponentially with energy when more than kT below the Fermi level. -

Photoinduced Electromotive Force on the Surface of Inn Epitaxial Layers
Photoinduced electromotive force on the surface of InN epitaxial layers B. K. Barick and S. Dhar* Department of Physics, Indian Institute of Technology, Bombay, Mumbai-400076, India *Corresponding Author’s Email: [email protected] Abstract: We report the generation of photo-induced electromotive force (EMF) on the surface of c-axis oriented InN epitaxial films grown on sapphire substrates. It has been found that under the illumination of above band gap light, EMFs of different magnitudes and polarities are developed on different parts of the surface of these layers. The effect is not the same as the surface photovoltaic or Dember potential effects, both of which result in the development of EMF across the layer thickness, not between different contacts on the surface. These layers are also found to show negative photoconductivity effect. Interplay between surface photo-EMF and negative photoconductivity result in a unique scenario, where the magnitude as well as the sign of the photo-induced change in conductivity become bias dependent. A theoretical model is developed, where both the effects are attributed to the 2D electron gas (2DEG) channel formed just below the film surface as a result of the transfer of electrons from certain donor- like-surfacestates, which are likely to be resulting due to the adsorption of certain groups/adatoms on the film surface. In the model, the photo-EMF effect is explained in terms of a spatially inhomogeneous distribution of these groups/adatoms over the surface resulting in a lateral non-uniformity in the depth distribution of the potential profile confining the 2DEG. -

Lecture 7: Extrinsic Semiconductors - Fermi Level
Lecture 7: Extrinsic semiconductors - Fermi level Contents 1 Dopant materials 1 2 EF in extrinsic semiconductors 5 3 Temperature dependence of carrier concentration 6 3.1 Low temperature regime (T < Ts)................7 3.2 Medium temperature regime (Ts < T < Ti)...........8 1 Dopant materials Typical doping concentrations in semiconductors are in ppm (10−6) and ppb (10−9). This small addition of `impurities' can cause orders of magnitude increase in conductivity. The impurity has to be of the right kind. For Si, n-type impurities are P, As, and Sb while p-type impurities are B, Al, Ga, and In. These form energy states close to the conduction and valence band and the ionization energies are a few tens of meV . Ge lies the same group IV as Si so that these elements are also used as impurities for Ge. The ionization energy data n-type impurities for Si and Ge are summarized in table 1. The ionization energy data for p-type impurities for Si and Ge is summarized in table 2. The dopant ionization energies for Ge are lower than Si. Ge has a lower band gap (0.67 eV ) compared to Si (1.10 eV ). Also, the Table 1: Ionization energies in meV for n-type impurities for Si and Ge. Typical values are close to room temperature thermal energy. Material P As Sb Si 45 54 39 Ge 12 12.7 9.6 1 MM5017: Electronic materials, devices, and fabrication Table 2: Ionization energies in meV for p-type impurities. Typical values are comparable to room temperature thermal energy. -

ELECTRONIC STRUCTURE of the SEMIMETALS Bi and Sb 1571
PHYSICAL REVIEW 8 VOLUME 52, NUMBER 3 15 JULY 1995-I Electronic structure of the semimetals Bi and Sh Yi Liu and Roland E. Allen Department ofPhysics, Texas ACkM University, Coliege Station, Texas 77843-4242 (Received 22 December 1994; revised manuscript received 13 March 1995) We have developed a third-neighbor tight-binding model, with spin-orbit coupling included, to treat the electronic properties of Bi and Sb. This model successfully reproduces the features near the Fermi surface that will be most important in semimetal-semiconductor device structures, including (a) the small overlap of valence and conduction bands, (b) the electron and hole efFective masses, and (c) the shapes of the electron and hole Fermi surfaces. The present tight-binding model treats these semimetallic proper- ties quantitatively, and it should, therefore, be useful for calculations of the electronic properties of pro- posed semimetal-semiconductor systems, including superlattices and resonant-tunneling devices. I. INTRQDUCTIQN energy gaps in the vicinity of the Fermi energy for Bi and Sb make a multiband treatment necessary; (ii) the band Recently, several groups have reported the successful alignment of these semimetal-semiconductor superlattices fabrication of semimetal-semiconductor superlattices, in- is indirect in momentum space, so a theoretical treatment cluding PbTe-Bi, ' CdTe-Bi, and GaSb-Sb. Bulk Bi and must represent a mixture of bulk states from different Sb are group-V semimetals. They have a weak overlap symmetry points of the Brillouin zone '" (iii) the carrier between the valence and conduction bands, which leads effective masses (particularly along the [111] growth to a small number of free electrons and holes. -

§6 – Free Electron Gas : §6 – Free Electron Gas
§6 – Free Electron Gas : §6 – Free Electron Gas 6.1 Overview of Electronic Properties The main species of solids are metals, semiconductors and insulators. One way to group these is by their resistivity: Metals – ~10−8−10−5 m Semiconductors – ~10−5−10 m Insulators – ~10−∞ m There is a striking difference in the temperature dependence of the resistivity: Metals – ρ increases with T (usually ∝T ) Semiconductors – ρ decreases with T Alloys have higher resistivity than its constituents; there is no law of mixing. This suggests some form of “impurity” mechanism The different species also have different optical properties. Metals – Opaque and lustrous (silvery) Insulators – often transparent or coloured The reasons for these differing properties can be explained by considering the density of electron states: 6.2 Free Electron (Fermi) Gas The simplest model of a metal was proposed by Fermi. This model transfers the ideas of electron orbitals in atoms into a macroscopic object. Thus, the fundamental behaviour of a metal comes from the Pauli exclusion principle. For now, we will ignore the crystal lattice. – 1 – Last Modified: 28/12/2006 §6 – Free Electron Gas : For this model, we make the following assumptions: ● The crystal comprises a fixed background of N identical positively charge nuclei and N electrons, which can move freely inside the crystal without seeing any of the nuclei (monovalent case); ● Coulomb interactions are negligible because the system is neutral overall This model works relatively well for alkali metals (Group 1 elements), such as Na, K, Rb and Cs. We would like to understand why electrons are only weakly scattered as they migrate through a metal.