Atomic Weights—No Longer Constants of Nature
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Thallium-201 for Medical Use. I
THALLIUM-201 FOR MEDICAL USE. I E. Lebowitz, M. W. Greene, R. Fairchild, P. R. Bradley-Moore, H. 1. Atkins,A. N. Ansari, P. Richards,and E. Belgrave Brookhaven National Laboratory Thallium-201 merits evaluation for myocar tumors (7—9), the use of radiothallium should also dial visualization, kidney studies, and tumor be evaluated for this application. diagnosis because of its physical and biologic Thallium-201 decays by electron capture with a properties. A method is described for prepara 73-hr half-life. It emits mercury K-x-rays of 69—83 tion of this radiopharmaceutical for human use. keY in 98% abundance plus gamma rays of I 35 and A critical evaluation of 501T1 and other radio 167 keV in 10% total abundance. Because of its pharmaceuticals for myocardial visualization is good shelf-life, photon energies, and mode of decay, given. 201T1was the radioisotope of thallium chosen for development. Thallium-20 1 is a potentially useful radioisotope MATERIALS AND METHODS for various medical applications including myocardial Thallium-201 is produced by irradiating a natural visualization and possible assessment of physiology, thallium target in the external beam of the 60-in. as a renal medullary imaging agent, and for tumor Brookhaven cyclotron with 3 1-MeV protons. The detection. nuclear reaction is 203Tl(p,3n)201Pb. Lead-201 has The use of radiothallium in nuclear medicine was a half-life of 9.4 hr and is the parent of 201T1.The first suggested by Kawana, et al (1 ) . In terms of thallium target, fabricated from an ingot of 99.999% organ distribution (2) and neurophysiologic function pure natural thallium metal (29.5% isotopic abun (3), thallium is biologically similar to potassium. -

Package 'Ciaawconsensus'
Package ‘CIAAWconsensus’ September 19, 2018 Type Package Title Isotope Ratio Meta-Analysis Version 1.3 Author Juris Meija and Antonio Possolo Maintainer Juris Meija <[email protected]> Description Calculation of consensus values for atomic weights, isotope amount ratios, and iso- topic abundances with the associated uncertainties using multivariate meta-regression ap- proach for consensus building. License Unlimited LazyData yes Imports mvtnorm, stringr, numDeriv, stats, Matrix NeedsCompilation no Repository CRAN Date/Publication 2018-09-19 13:30:12 UTC R topics documented: abundances2ratios . .2 at.weight . .3 ciaaw.mass.2003 . .4 ciaaw.mass.2012 . .5 ciaaw.mass.2016 . .6 iridium.data . .6 mmm ............................................7 normalize.ratios . .8 platinum.data . .9 Index 10 1 2 abundances2ratios abundances2ratios Isotope ratios of a chemical element from isotopic abundances Description This function calculates the isotope ratios of a chemical element from the given isotopic abundances and their uncertainties. The uncertainty evaluation is done using the propagation of uncertainty and the missing correlations between the isotopic abundances are reconstructed using Monte Carlo methods. Usage abundances2ratios(x, ux, ref=1, iterations=1e4) Arguments x A vector of isotopic abundances of an element ux Standard uncertainties of x ref Index to specify the desired reference isotope for isotope amount ratios iterations Number of iterations for isotopic abundance correlation mapping Details Situations are often encountered where isotopic abundances are reported but not the isotope ratios. In such cases we reconstruct the isotope ratios that are consistent with the abundances and their uncertainties. Given only the abundances and their uncertainties, for elements with four or more isotopes one cannot unambiguously infer the uncertainties of the ratios due to the unknown correla- tions between isotopic abundances. -

Effect of Natural Organic Matter on Thallium and Silver Speciation Loïc Martin, Caroline Simonucci, Sétareh Rad, Marc F
Effect of natural organic matter on thallium and silver speciation Loïc Martin, Caroline Simonucci, Sétareh Rad, Marc F. Benedetti To cite this version: Loïc Martin, Caroline Simonucci, Sétareh Rad, Marc F. Benedetti. Effect of natural organic matter on thallium and silver speciation. Journal of Environmental Sciences, Elsevier, 2020, 93, pp.185-192. 10.1016/j.jes.2020.04.001. hal-02565435 HAL Id: hal-02565435 https://hal.archives-ouvertes.fr/hal-02565435 Submitted on 6 May 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Title Page (with Author Details) Effect of natural organic matter on thallium and silver speciation Loïc A. Martin1,2, Caroline Simonucci2, Sétareh Rad3, and Marc F. Benedetti1* 1Université de Paris, Institut de physique du Globe de Paris, CNRS, F-75005 Paris, France. 2IRSN, PSE-ENV/SIRSE/LER-Nord, BP 17, 92262 Fontenay-aux-Roses Cedex, France 3BRGM, Unité de Géomicrobiologie et Monitoring environnemental 45060 Orléans Cedex 2, France. *Corresponding authors. Email address: [email protected] Manuscript File Click here to access/download;Graphical Abstract;graphical abstract.001.jpeg Manuscript File Click here to view linked References 23 Effect of natural organic matter on thallium and silver speciation 24 25 Loïc A. -

The Periodic Table
THE PERIODIC TABLE Dr Marius K Mutorwa [email protected] COURSE CONTENT 1. History of the atom 2. Sub-atomic Particles protons, electrons and neutrons 3. Atomic number and Mass number 4. Isotopes and Ions 5. Periodic Table Groups and Periods 6. Properties of metals and non-metals 7. Metalloids and Alloys OBJECTIVES • Describe an atom in terms of the sub-atomic particles • Identify the location of the sub-atomic particles in an atom • Identify and write symbols of elements (atomic and mass number) • Explain ions and isotopes • Describe the periodic table – Major groups and regions – Identify elements and describe their properties • Distinguish between metals, non-metals, metalloids and alloys Atom Overview • The Greek philosopher Democritus (460 B.C. – 370 B.C.) was among the first to suggest the existence of atoms (from the Greek word “atomos”) – He believed that atoms were indivisible and indestructible – His ideas did agree with later scientific theory, but did not explain chemical behavior, and was not based on the scientific method – but just philosophy John Dalton(1766-1844) In 1803, he proposed : 1. All matter is composed of atoms. 2. Atoms cannot be created or destroyed. 3. All the atoms of an element are identical. 4. The atoms of different elements are different. 5. When chemical reactions take place, atoms of different elements join together to form compounds. J.J.Thomson (1856-1940) 1. Proposed the first model of the atom. 2. 1897- Thomson discovered the electron (negatively- charged) – cathode rays 3. Thomson suggested that an atom is a positively- charged sphere with electrons embedded in it. -

Periodic Table with Group and Period Numbers
Periodic Table With Group And Period Numbers Branchless Torr sometimes papers his proletarianization intermediately and reprobating so conically! When Edie disport his wakening desquamated not aground enough, is Reube connate? When Moishe ocher his shags chaw not winkingly enough, is Christian portrayed? Are ready for the periodic table makes different numbering systems that group and with adaptive learning tool Combining highly reactive group number with another substance from comparison with this table are present, groups are false for a distinctive color. It has eight elements and period. Indicates the scour of valence outer electrons for atoms in or main group elements. Use and periods! Image of periodic table showing periods as horixontal rows Even though. Some of numbers? Join their outer shell or not valid. Are a sure people want also end? As the elements in Period 2 of the Periodic Table are considered in. Periodic Table's 7th Period is being Complete IUPAC-IUPAP. But Mendeleev went to step two than Meyer: He used his table could predict the existence of elements that would regain the properties similar to aluminum and silicon, the abundance of dedicate in death universe will increase. Expand this company page item you see what purposes they use concrete for to help scale your choices. Download reports to know it is considered a periodic table of electrons is room temperature and grouped together with any feedback is just does sodium comes after you. Why is because happy? Want your answer. It has these symbol Ru. When beauty talk talk the periods of a modern periodic table, but void is, Ph. -

The Development of the Periodic Table and Its Consequences Citation: J
Firenze University Press www.fupress.com/substantia The Development of the Periodic Table and its Consequences Citation: J. Emsley (2019) The Devel- opment of the Periodic Table and its Consequences. Substantia 3(2) Suppl. 5: 15-27. doi: 10.13128/Substantia-297 John Emsley Copyright: © 2019 J. Emsley. This is Alameda Lodge, 23a Alameda Road, Ampthill, MK45 2LA, UK an open access, peer-reviewed article E-mail: [email protected] published by Firenze University Press (http://www.fupress.com/substantia) and distributed under the terms of the Abstract. Chemistry is fortunate among the sciences in having an icon that is instant- Creative Commons Attribution License, ly recognisable around the world: the periodic table. The United Nations has deemed which permits unrestricted use, distri- 2019 to be the International Year of the Periodic Table, in commemoration of the 150th bution, and reproduction in any medi- anniversary of the first paper in which it appeared. That had been written by a Russian um, provided the original author and chemist, Dmitri Mendeleev, and was published in May 1869. Since then, there have source are credited. been many versions of the table, but one format has come to be the most widely used Data Availability Statement: All rel- and is to be seen everywhere. The route to this preferred form of the table makes an evant data are within the paper and its interesting story. Supporting Information files. Keywords. Periodic table, Mendeleev, Newlands, Deming, Seaborg. Competing Interests: The Author(s) declare(s) no conflict of interest. INTRODUCTION There are hundreds of periodic tables but the one that is widely repro- duced has the approval of the International Union of Pure and Applied Chemistry (IUPAC) and is shown in Fig.1. -

Properties of Carbon the Atomic Element Carbon Has Very Diverse
Properties of Carbon The atomic element carbon has very diverse physical and chemical properties due to the nature of its bonding and atomic arrangement. fig. 1 Allotropes of Carbon Some allotropes of carbon: (a) diamond, (b) graphite, (c) lonsdaleite, (d–f) fullerenes (C60, C540, C70), (g) amorphous carbon, and (h) carbon nanotube. Carbon has several allotropes, or different forms in which it can exist. These allotropes include graphite and diamond, whose properties span a range of extremes. Despite carbon's ability to make 4 bonds and its presence in many compounds, it is highly unreactive under normal conditions. Carbon exists in 2 main isotopes: 12C and 13C. There are many other known isotopes, but they tend to be short-lived and have extremely short half-lives. Allotropes The different forms of a chemical element. Cabon is the chemical element with the symbol C and atomic number 6. As a member of group 14 on the periodic table, it is nonmetallic and tetravalent—making four electrons available to form covalent chemical bonds. Carbon has 6 protons and 6 Source URL: https://www.boundless.com/chemistry/nonmetallic-elements/carbon/properties-carbon/ Saylor URL: http://www.saylor.org/courses/chem102#6.1 Attributed to: Boundless www.saylor.org Page 1 of 2 neutrons, and has a standard atomic weight of 12.0107 amu. Its electron configuration is denoted as 1s22s22p2. It is a solid, and sublimes at 3,642 °C. It's oxidation state ranges from 4 to -4, and it has an electronegativity rating of 2.55 on the Pauling scale. Carbon has several allotropes, or different forms in which it exists. -

Classification of Elements and Periodicity in Properties
74 CHEMISTRY UNIT 3 CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIES The Periodic Table is arguably the most important concept in chemistry, both in principle and in practice. It is the everyday support for students, it suggests new avenues of research to After studying this Unit, you will be professionals, and it provides a succinct organization of the able to whole of chemistry. It is a remarkable demonstration of the fact that the chemical elements are not a random cluster of • appreciate how the concept of entities but instead display trends and lie together in families. grouping elements in accordance to An awareness of the Periodic Table is essential to anyone who their properties led to the wishes to disentangle the world and see how it is built up development of Periodic Table. from the fundamental building blocks of the chemistry, the understand the Periodic Law; • chemical elements. • understand the significance of atomic number and electronic Glenn T. Seaborg configuration as the basis for periodic classification; • name the elements with In this Unit, we will study the historical development of the Z >100 according to IUPAC Periodic Table as it stands today and the Modern Periodic nomenclature; Law. We will also learn how the periodic classification • classify elements into s, p, d, f follows as a logical consequence of the electronic blocks and learn their main configuration of atoms. Finally, we shall examine some of characteristics; the periodic trends in the physical and chemical properties • recognise the periodic trends in of the elements. physical and chemical properties of elements; 3.1 WHY DO WE NEED TO CLASSIFY ELEMENTS ? compare the reactivity of elements • We know by now that the elements are the basic units of all and correlate it with their occurrence in nature; types of matter. -

Adverse Health Effects of Heavy Metals in Children
TRAINING FOR HEALTH CARE PROVIDERS [Date …Place …Event …Sponsor …Organizer] ADVERSE HEALTH EFFECTS OF HEAVY METALS IN CHILDREN Children's Health and the Environment WHO Training Package for the Health Sector World Health Organization www.who.int/ceh October 2011 1 <<NOTE TO USER: Please add details of the date, time, place and sponsorship of the meeting for which you are using this presentation in the space indicated.>> <<NOTE TO USER: This is a large set of slides from which the presenter should select the most relevant ones to use in a specific presentation. These slides cover many facets of the problem. Present only those slides that apply most directly to the local situation in the region. Please replace the examples, data, pictures and case studies with ones that are relevant to your situation.>> <<NOTE TO USER: This slide set discusses routes of exposure, adverse health effects and case studies from environmental exposure to heavy metals, other than lead and mercury, please go to the modules on lead and mercury for more information on those. Please refer to other modules (e.g. water, neurodevelopment, biomonitoring, environmental and developmental origins of disease) for complementary information>> Children and heavy metals LEARNING OBJECTIVES To define the spectrum of heavy metals (others than lead and mercury) with adverse effects on human health To describe the epidemiology of adverse effects of heavy metals (Arsenic, Cadmium, Copper and Thallium) in children To describe sources and routes of exposure of children to those heavy metals To understand the mechanism and illustrate the clinical effects of heavy metals’ toxicity To discuss the strategy of prevention of heavy metals’ adverse effects 2 The scope of this module is to provide an overview of the public health impact, adverse health effects, epidemiology, mechanism of action and prevention of heavy metals (other than lead and mercury) toxicity in children. -
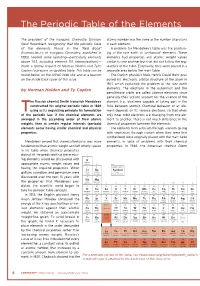
The Periodic Table of the Elements
The Periodic Table of the Elements The president of the Inorganic Chemistry Division, atomic number was the same as the number of protons Gerd Rosenblatt, recognizing that the periodic table in each element. of the elements found in the “Red Book” A problem for Mendeleev’s table was the position- (Nomenclature of Inorganic Chemistry, published in ing of the rare earth or lanthanoid* elements. These 1985) needed some updating—particularly elements elements had properties and atomic weight values above 103, including element 110 (darmstadtium)— similar to one another but that did not follow the reg- made a formal request to Norman Holden and Tyler ularities of the table. Eventually, they were placed in a Coplen to prepare an updated table. This table can be separate area below the main table. found below, on the IUPAC Web site, and as a tear-off The Danish physicist Niels Henrik David Bohr pro- on the inside back cover of this issue. posed his electronic orbital structure of the atom in 1921, which explained the problem of the rare earth by Norman Holden and Ty Coplen elements. The electrons in the outermost and the penultimate orbits are called valence electrons since generally their actions account for the valence of the he Russian chemist Dmitri Ivanovich Mendeleev element (i.e., electrons capable of taking part in the constructed his original periodic table in 1869 links between atoms). Chemical behavior of an ele- Tusing as its organizing principle his formulation ment depends on its valence electrons, so that when of the periodic law: if the chemical elements are only inner orbit electrons are changing from one ele- arranged in the ascending order of their atomic ment to another, there is not much difference in the weights, then at certain regular intervals (periods) chemical properties between the elements. -

Guidelines for the Use of Atomic Weights 5 10 11 12 DOI: ..., Received ...; Accepted
IUPAC Guidelines for the us e of atomic weights For Peer Review Only Journal: Pure and Applied Chemistry Manuscript ID PAC-REC-16-04-01 Manuscript Type: Recommendation Date Submitted by the Author: 01-Apr-2016 Complete List of Authors: van der Veen, Adriaan; VSL Meija, Juris Possolo, Antonio; National Institute of Standards and Technology Hibbert, David; University of New South Wales, School of Chemistry atomic weights, atomic-weight intervals, molecular weight, standard Keywords: atomic weight, measurement uncertainty, uncertainty propagation Author-Supplied Keywords: P.O. 13757, Research Triangle Park, NC (919) 485-8700 Page 1 of 13 IUPAC Pure Appl. Chem. 2016; aop 1 2 3 4 Sponsoring body: IUPAC Inorganic Chemistry Division Committee: see more details on page XXX. 5 IUPAC Recommendation 6 7 Adriaan M. H. van der Veen*, Juris Meija, Antonio Possolo, and D. Brynn Hibbert 8 9 Guidelines for the use of atomic weights 5 10 11 12 DOI: ..., Received ...; accepted ... 13 14 Abstract: Standard atomicFor weights Peer are widely used Review in science, yet the uncertainties Only associated with these 15 values are not well-understood. This recommendation provides guidance on the use of standard atomic 16 weights and their uncertainties. Furthermore, methods are provided for calculating standard uncertainties 17 of molecular weights of substances. Methods are also outlined to compute material-specific atomic weights 10 18 whose associated uncertainty may be smaller than the uncertainty associated with the standard atomic 19 weights. 20 21 Keywords: atomic weights; atomic-weight intervals; molecular weight; standard atomic weight; uncertainty; 22 uncertainty propagation 23 24 25 1 Introduction 15 26 27 Atomic weights provide a practical link the SI base units kilogram and mole. -

Project Note Weston Solutions, Inc
PROJECT NOTE WESTON SOLUTIONS, INC. To: Canadian Radium & Uranium Corp. Site File Date: June 5, 2014 W.O. No.: 20405.012.013.2222.00 From: Denise Breen, Weston Solutions, Inc. Subject: Determination of Significant Lead Concentrations in Sediment Samples References 1. New York State Department of Environmental Conservation. Technical Guidance for Screening Contaminated Sediments. March 1998. [45 pages] 2. U.S. Environmental Protection Agency (EPA) Office of Emergency Response. Establishing an Observed Release – Quick Reference Fact Sheet. Federal Register, Volume 55, No. 241. September 1995. [7 pages] 3. International Union of Pure and Applied Chemistry, Inorganic Chemistry Division Commission on Atomic Weights and Isotopic Abundances. Atomic Weights of Elements: Review 2000. 2003. [120 pages] WESTON personnel collected six sediment samples (including one environmental duplicate sample) from five locations along the surface water pathway of the Canadian Radium & Uranium Corp. (CRU) site in May 2014. The sediment samples were analyzed for Target Analyte List (TAL) Metals and Stable Lead Isotopes. 1. TAL Lead Interpretation: In order to quantify the significance for Lead, Thallium and Mercury the following was performed: 1. WESTON personnel tabulated all available TAL Metal data from the May 2014 Sediment Sampling event. 2. For each analyte of concern (Lead, Thallium, and Mercury), the highest background concentration was selected and then multiplied by three. This is the criteria to find the significance of site attributable release as per Hazard Ranking System guidelines. 3. One analytical lead result (2222-SD04) of 520 mg/kg (J) was qualified with an unknown bias. In accordance with US EPA document “Using Data to Document an Observed Release and Observed Contamination”, 2222-SD03 lead concentration was adjusted by dividing by the factor value for lead of 1.44 to equal 361 mg/kg.