DOCSLIB.ORG

Find Each Measure. 1. SOLUTION: If an Angle Is

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Find Each Measure. 1. SOLUTION: If an Angle Is 9-4 Inscribed Angles Find each measure. 3. 1. SOLUTION: SOLUTION: If an angle is inscribed in a circle, then the measure of the angle equals one half the measure of its Here, is a semi-circle. So, intercepted arc. Therefore, If an angle is inscribed in a circle, then the measure of the angle equals one half the measure of its ANSWER: intercepted arc. So, 30 Therefore, 2. ANSWER: 66 4. SCIENCE The diagram shows how light bends in a raindrop to make the colors of the rainbow. If , what is ? SOLUTION: If an angle is inscribed in a circle, then the measure of the angle equals one half the measure of its intercepted arc. Therefore, ANSWER: 126 SOLUTION: If an angle is inscribed in a circle, then the measure of the angle equals one half the measure of its intercepted arc. Therefore, ANSWER: 72 eSolutions Manual - Powered by Cognero Page 1 9-4 Inscribed Angles ALGEBRA Find each measure. 5. SOLUTION: Given: Prove: SOLUTION: If two inscribed angles of a circle intercept the same arc or congruent arcs, then the angles are congruent. So, Therefore, ANSWER: Proof: 54 Statements (Reasons) 1. (Given) 2. (If minor arcs are , their 6. corresponding chords are .) 3. intercepts . intercepts . intercepts . intercepts . (Def. of intercepted arc) 4. (Inscribed of same arc are .) 5. (ASA) SOLUTION: ANSWER: If two inscribed angles of a circle intercept the same Given: arc or congruent arcs, then the angles are congruent. Prove: So, Therefore, ANSWER: 36 Proof: 7. PROOF Write a two-column proof. Statements (Reasons) Given: 1. (Given) Prove: 2. (If minor arcs are , their corresponding chords are .) 3. intercepts . intercepts . intercepts . intercepts . (Def. of eSolutions Manual - Powered by Cognero Page 2 9-4 Inscribed Angles intercepted arc) 9. x 4. (Inscribed of same arc are .) 5. (ASA) STRUCTURE Find each value. 8. SOLUTION: An inscribed angle of a triangle intercepts a diameter or semicircle if and only if the angle is a right angle. So, Since The sum of the measures of the angles of a triangle is SOLUTION: 180. So, An inscribed angle of a triangle intercepts a diameter or semicircle if and only if the angle is a right angle. So, The sum of the measures of the angles of a triangle is 180. So, ANSWER: 25 10. and Therefore, ANSWER: 62 SOLUTION: If a quadrilateral is inscribed in a circle, then its opposite angles are supplementary. Solve the two equations to find the values of x and y. Use the values of the variables to find and . ANSWER: 122; 80 eSolutions Manual - Powered by Cognero Page 3 9-4 Inscribed Angles Find each measure. 13. 11. SOLUTION: SOLUTION: The sum of the measures of the central angles of a If an angle is inscribed in a circle, then the measure circle with no interior points in common is 360. So, of the angle equals one half the measure of its intercepted arc. Therefore, ANSWER: If an angle is inscribed in a circle, then the measure 162 of the angle equals one half the measure of its intercepted arc. Therefore, 12. ANSWER: 70 14. SOLUTION: If an angle is inscribed in a circle, then the measure of the angle equals one half the measure of its intercepted arc. Therefore, SOLUTION: If an angle is inscribed in a circle, then the measure ANSWER: of the angle equals one half the measure of its 46 intercepted arc. Therefore, ANSWER: 48 eSolutions Manual - Powered by Cognero Page 4 9-4 Inscribed Angles 15. ALGEBRA Find each measure. 17. SOLUTION: Here, SOLUTION: The arc is a semicircle. So, If two inscribed angles of a circle intercept the same If an angle is inscribed in a circle, then the measure arc or congruent arcs, then the angles are congruent. of the angle equals one half the measure of its So, intercepted arc. So, ANSWER: Therefore, 32 ANSWER: 140 18. 16. SOLUTION: If two inscribed angles of a circle intercept the same arc or congruent arcs, then the angles are congruent. SOLUTION: So, Here, The arc is a semicircle. So, Therefore, Then, If an angle is inscribed in a circle, then the measure ANSWER: of the angle equals one half the measure of its 34 intercepted arc. Therefore, ANSWER: 66 eSolutions Manual - Powered by Cognero Page 5 9-4 Inscribed Angles 19. PROOF Write the specified type of proof. 21. paragraph proof Given: Prove: SOLUTION: If two inscribed angles of a circle intercept the same arc or congruent arcs, then the angles are congruent. ∠ ∠ ∠ Since A and B both intercept arc CD , m A = SOLUTION: m∠B. Proof: Given means that Therefore, m∠A = 5(4) or 20. Since and ANSWER: , the equation becomes 20 . Multiplying each side of the 20. equation by 2 results in . ANSWER: Proof: Given means that . Since and SOLUTION: , the equation becomes If two inscribed angles of a circle intercept the same arc or congruent arcs, then the angles are congruent. Multiplying each side of the Since ∠C and ∠D both intercept arc AB, m∠C = m∠D. equation by 2 results in . Therefore, m∠C = 5(10) – 3 or 47. ANSWER: 47 eSolutions Manual - Powered by Cognero Page 6 9-4 Inscribed Angles 22. two-column proof ALGEBRA Find each value. Given: Prove: 23. x SOLUTION: Statements (Reasons): SOLUTION: 1. (Given) An inscribed angle of a triangle intercepts a diameter 2. (Inscribed intercepting same arc or semicircle if and only if the angle is a right angle. are .) So, 3. (Vertical are .) The sum of the measures of the angles of a triangle is 4. (AA Similarity) 180. So, ANSWER: Statements (Reasons): 1. (Given) 2. (Inscribed intercepting same arc ANSWER: are .) 30 3. (Vertical are .) 4. (AA Similarity) 24. SOLUTION: An inscribed angle of a triangle intercepts a diameter or semicircle if and only if the angle is a right angle. So, The sum of the measures of the angles of a triangle is 180. So, Therefore, ANSWER: 60 eSolutions Manual - Powered by Cognero Page 7 9-4 Inscribed Angles 25. x STRUCTURE Find each measure. 27. SOLUTION: SOLUTION: An inscribed angle of a triangle intercepts a diameter or semicircle if and only if the angle is a right angle. If a quadrilateral is inscribed in a circle, then its So, opposite angles are supplementary. The sum of the measures of the angles of a triangle is 180. So, Therefore, ANSWER: 135 ANSWER: 28. 12.75 26. SOLUTION: If a quadrilateral is inscribed in a circle, then its opposite angles are supplementary. SOLUTION: An inscribed angle of a triangle intercepts a diameter or semicircle if and only if the angle is a right angle. Therefore, So, The sum of the measures of the angles of a triangle is ANSWER: 180. So, 80 Therefore, ANSWER: 51.75 eSolutions Manual - Powered by Cognero Page 8 9-4 Inscribed Angles 29. Proof: By arc addition and the definitions of arc SOLUTION: measure and the sum of central angles, If a quadrilateral is inscribed in a circle, then its . Since by Theorem 10.6 opposite angles are supplementary. and , but , so or Therefore, 180. This makes ∠C and ∠A supplementary. ANSWER: Because the sum of the measures of the interior 106 angles of a quadrilateral is 360, . But 30. , so , making them supplementary also. ANSWER: Given: Quadrilateral ABCD is inscribed in . Prove: and are supplementary. and are supplementary. SOLUTION: If a quadrilateral is inscribed in a circle, then its opposite angles are supplementary. Proof: By arc addition and the definitions of arc Therefore, measure and the sum of central angles, ANSWER: . Since by Theorem 10.6 93 and 31. PROOF Write a paragraph proof for Theorem 9.9. , but SOLUTION: , so Given: Quadrilateral ABCD is inscribed in . Prove: and are supplementary. or 180. This makes ∠C and ∠A supplementary. and are supplementary. Because the sum of the measures of the interior angles of a quadrilateral is 360, eSolutions Manual - Powered by Cognero Page 9 9-4 Inscribed Angles . But 33. , so , making them supplementary also. SOLUTION: Since all the sides of the stop sign are congruent chords of the circle, all the corresponding arcs are SIGNS: A stop sign in the shape of a regular congruent. There are eight adjacent arcs that make octagon is inscribed in a circle. Find each up the circle, so their sum is 360. Thus, the measure measure. of each arc joining consecutive vertices is of 360 or 45. Since ∠RLQ is inscribed in the circle, its measure equals one half the measure of its intercepted arc QR. 32. Therefore, the measure of ∠RLQ is 22.5. SOLUTION: Since all the sides of the stop sign are congruent chords of the circle, the corresponding arcs are ANSWER: congruent. There are eight adjacent arcs that make 22.5 up the circle, so their sum is 360. Thus, the measure 34. of each arc joining consecutive vertices is of 360 or 45. SOLUTION: If an angle is inscribed in a circle, then the measure of the angle equals one half the measure of its Therefore, measure of arc NPQ is 135. intercepted arc. So, ANSWER: The sum of the measures of the central angles of a 135 circle with no interior points in common is 360. Here, 360 is divided into 8 equal arcs and each arc measures Then, Therefore, ANSWER: 112.5 eSolutions Manual - Powered by Cognero Page 10 9-4 Inscribed Angles 35. SOLUTION: If an angle is inscribed in a circle, then the measure of the angle equals one half the measure of its intercepted arc. So, SOLUTION: The sum of the measures of the central angles of a a.
Load more

Recommended publications
  • A Genetic Context for Understanding the Trigonometric Functions Danny Otero Xavier University, [email protected]
    Ursinus College Digital Commons @ Ursinus College Transforming Instruction in Undergraduate Pre-calculus and Trigonometry Mathematics via Primary Historical Sources (TRIUMPHS) Spring 3-2017 A Genetic Context for Understanding the Trigonometric Functions Danny Otero Xavier University, [email protected] Follow this and additional works at: https://digitalcommons.ursinus.edu/triumphs_precalc Part of the Curriculum and Instruction Commons, Educational Methods Commons, Higher Education Commons, and the Science and Mathematics Education Commons Click here to let us know how access to this document benefits oy u. Recommended Citation Otero, Danny, "A Genetic Context for Understanding the Trigonometric Functions" (2017). Pre-calculus and Trigonometry. 1. https://digitalcommons.ursinus.edu/triumphs_precalc/1 This Course Materials is brought to you for free and open access by the Transforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) at Digital Commons @ Ursinus College. It has been accepted for inclusion in Pre-calculus and Trigonometry by an authorized administrator of Digital Commons @ Ursinus College. For more information, please contact [email protected]. A Genetic Context for Understanding the Trigonometric Functions Daniel E. Otero∗ July 22, 2019 Trigonometry is concerned with the measurements of angles about a central point (or of arcs of circles centered at that point) and quantities, geometrical and otherwise, that depend on the sizes of such angles (or the lengths of the corresponding arcs). It is one of those subjects that has become a standard part of the toolbox of every scientist and applied mathematician. It is the goal of this project to impart to students some of the story of where and how its central ideas first emerged, in an attempt to provide context for a modern study of this mathematical theory.
    [Show full text]
  • Centroids by Composite Areas.Pptx
    Centroids Method of Composite Areas A small boy swallowed some coins and was taken to a hospital. When his grandmother telephoned to ask how he was a nurse said 'No change yet'. Centroids ¢ Previously, we developed a general formulation for finding the centroid for a series of n areas n xA ∑ ii i=1 x = n A ∑ i i=1 2 Centroids by Composite Areas Monday, November 12, 2012 1 Centroids ¢ xi was the distance from the y-axis to the local centroid of the area Ai n xA ∑ ii i=1 x = n A ∑ i i=1 3 Centroids by Composite Areas Monday, November 12, 2012 Centroids ¢ If we can break up a shape into a series of smaller shapes that have predefined local centroid locations, we can use this formula to locate the centroid of the composite shape n xA ∑ ii i=1 x = n A ∑ i 4 Centroids by Composite Areas i=1 Monday, November 12, 2012 2 Centroid by Composite Bodies ¢ There is a table in the back cover of your book that gives you the location of local centroids for a select group of shapes ¢ The point labeled C is the location of the centroid of that shape. 5 Centroids by Composite Areas Monday, November 12, 2012 Centroid by Composite Bodies ¢ Please note that these are local centroids, they are given in reference to the x and y axes as shown in the table. 6 Centroids by Composite Areas Monday, November 12, 2012 3 Centroid by Composite Bodies ¢ For example, the centroid location of the semicircular area has the y-axis through the center of the area and the x-axis at the bottom of the area ¢ The x-centroid would be located at 0 and the y-centroid would be located
    [Show full text]
  • Geometric Exercises in Paper Folding
    MATH/STAT. T. SUNDARA ROW S Geometric Exercises in Paper Folding Edited and Revised by WOOSTER WOODRUFF BEMAN PROFESSOR OF MATHEMATICS IN THE UNIVERSITY OF MICHIGAK and DAVID EUGENE SMITH PROFESSOR OF MATHEMATICS IN TEACHERS 1 COLLEGE OF COLUMBIA UNIVERSITY WITH 87 ILLUSTRATIONS THIRD EDITION CHICAGO ::: LONDON THE OPEN COURT PUBLISHING COMPANY 1917 & XC? 4255 COPYRIGHT BY THE OPEN COURT PUBLISHING Co, 1901 PRINTED IN THE UNITED STATES OF AMERICA hn HATH EDITORS PREFACE. OUR attention was first attracted to Sundara Row s Geomet rical Exercises in Paper Folding by a reference in Klein s Vor- lesungen iiber ausgezucihlte Fragen der Elementargeometrie. An examination of the book, obtained after many vexatious delays, convinced us of its undoubted merits and of its probable value to American teachers and students of geometry. Accordingly we sought permission of the author to bring out an edition in this country, wnich permission was most generously granted. The purpose of the book is so fully set forth in the author s introduction that we need only to say that it is sure to prove of interest to every wide-awake teacher of geometry from the graded school to the college. The methods are so novel and the results so easily reached that they cannot fail to awaken enthusiasm. Our work as editors in this revision has been confined to some slight modifications of the proofs, some additions in the way of references, and the insertion of a considerable number of half-tone reproductions of actual photographs instead of the line-drawings of the original. W. W.
    [Show full text]
  • Circle Theorems
    Circle theorems A LEVEL LINKS Scheme of work: 2b. Circles – equation of a circle, geometric problems on a grid Key points • A chord is a straight line joining two points on the circumference of a circle. So AB is a chord. • A tangent is a straight line that touches the circumference of a circle at only one point. The angle between a tangent and the radius is 90°. • Two tangents on a circle that meet at a point outside the circle are equal in length. So AC = BC. • The angle in a semicircle is a right angle. So angle ABC = 90°. • When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference. So angle AOB = 2 × angle ACB. • Angles subtended by the same arc at the circumference are equal. This means that angles in the same segment are equal. So angle ACB = angle ADB and angle CAD = angle CBD. • A cyclic quadrilateral is a quadrilateral with all four vertices on the circumference of a circle. Opposite angles in a cyclic quadrilateral total 180°. So x + y = 180° and p + q = 180°. • The angle between a tangent and chord is equal to the angle in the alternate segment, this is known as the alternate segment theorem. So angle BAT = angle ACB. Examples Example 1 Work out the size of each angle marked with a letter. Give reasons for your answers. Angle a = 360° − 92° 1 The angles in a full turn total 360°. = 268° as the angles in a full turn total 360°.
    [Show full text]
  • Angles ANGLE Topics • Coterminal Angles • Defintion of an Angle
    Angles ANGLE Topics • Coterminal Angles • Defintion of an angle • Decimal degrees to degrees, minutes, seconds by hand using the TI-82 or TI-83 Plus • Degrees, seconds, minutes changed to decimal degree by hand using the TI-82 or TI-83 Plus • Standard position of an angle • Positive and Negative angles ___________________________________________________________________________ Definition: Angle An angle is created when a half-ray (the initial side of the angle) is drawn out of a single point (the vertex of the angle) and the ray is rotated around the point to another location (becoming the terminal side of the angle). An angle is created when a half-ray (initial side of angle) A: vertex point of angle is drawn out of a single point (vertex) AB: Initial side of angle. and the ray is rotated around the point to AC: Terminal side of angle another location (becoming the terminal side of the angle). Hence angle A is created (also called angle BAC) STANDARD POSITION An angle is in "standard position" when the vertex is at the origin and the initial side of the angle is along the positive x-axis. Recall: polynomials in algebra have a standard form (all the terms have to be listed with the term having the highest exponent first). In trigonometry, there is a standard position for angles. In this way, we are all talking about the same thing and are not trying to guess if your math solution and my math solution are the same. Not standard position. Not standard position. This IS standard position. Initial side not along Initial side along negative Initial side IS along the positive x-axis.
    [Show full text]
  • 20. Geometry of the Circle (SC)
    20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord.
    [Show full text]
  • Calculus Terminology
    AP Calculus BC Calculus Terminology Absolute Convergence Asymptote Continued Sum Absolute Maximum Average Rate of Change Continuous Function Absolute Minimum Average Value of a Function Continuously Differentiable Function Absolutely Convergent Axis of Rotation Converge Acceleration Boundary Value Problem Converge Absolutely Alternating Series Bounded Function Converge Conditionally Alternating Series Remainder Bounded Sequence Convergence Tests Alternating Series Test Bounds of Integration Convergent Sequence Analytic Methods Calculus Convergent Series Annulus Cartesian Form Critical Number Antiderivative of a Function Cavalieri’s Principle Critical Point Approximation by Differentials Center of Mass Formula Critical Value Arc Length of a Curve Centroid Curly d Area below a Curve Chain Rule Curve Area between Curves Comparison Test Curve Sketching Area of an Ellipse Concave Cusp Area of a Parabolic Segment Concave Down Cylindrical Shell Method Area under a Curve Concave Up Decreasing Function Area Using Parametric Equations Conditional Convergence Definite Integral Area Using Polar Coordinates Constant Term Definite Integral Rules Degenerate Divergent Series Function Operations Del Operator e Fundamental Theorem of Calculus Deleted Neighborhood Ellipsoid GLB Derivative End Behavior Global Maximum Derivative of a Power Series Essential Discontinuity Global Minimum Derivative Rules Explicit Differentiation Golden Spiral Difference Quotient Explicit Function Graphic Methods Differentiable Exponential Decay Greatest Lower Bound Differential
    [Show full text]
  • Foundations of Geometry
    California State University, San Bernardino CSUSB ScholarWorks Theses Digitization Project John M. Pfau Library 2008 Foundations of geometry Lawrence Michael Clarke Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd-project Part of the Geometry and Topology Commons Recommended Citation Clarke, Lawrence Michael, "Foundations of geometry" (2008). Theses Digitization Project. 3419. https://scholarworks.lib.csusb.edu/etd-project/3419 This Thesis is brought to you for free and open access by the John M. Pfau Library at CSUSB ScholarWorks. It has been accepted for inclusion in Theses Digitization Project by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. Foundations of Geometry A Thesis Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degree Master of Arts in Mathematics by Lawrence Michael Clarke March 2008 Foundations of Geometry A Thesis Presented to the Faculty of California State University, San Bernardino by Lawrence Michael Clarke March 2008 Approved by: 3)?/08 Murran, Committee Chair Date _ ommi^yee Member Susan Addington, Committee Member 1 Peter Williams, Chair, Department of Mathematics Department of Mathematics iii Abstract In this paper, a brief introduction to the history, and development, of Euclidean Geometry will be followed by a biographical background of David Hilbert, highlighting significant events in his educational and professional life. In an attempt to add rigor to the presentation of Geometry, Hilbert defined concepts and presented five groups of axioms that were mutually independent yet compatible, including introducing axioms of congruence in order to present displacement.
    [Show full text]
  • Archimedes and the Arbelos1 Bobby Hanson October 17, 2007
    Archimedes and the Arbelos1 Bobby Hanson October 17, 2007 The mathematician’s patterns, like the painter’s or the poet’s must be beautiful; the ideas like the colours or the words, must fit together in a harmonious way. Beauty is the first test: there is no permanent place in the world for ugly mathematics. — G.H. Hardy, A Mathematician’s Apology ACBr 1 − r Figure 1. The Arbelos Problem 1. We will warm up on an easy problem: Show that traveling from A to B along the big semicircle is the same distance as traveling from A to B by way of C along the two smaller semicircles. Proof. The arc from A to C has length πr/2. The arc from C to B has length π(1 − r)/2. The arc from A to B has length π/2. ˜ 1My notes are shamelessly stolen from notes by Tom Rike, of the Berkeley Math Circle available at http://mathcircle.berkeley.edu/BMC6/ps0506/ArbelosBMC.pdf . 1 2 If we draw the line tangent to the two smaller semicircles, it must be perpendicular to AB. (Why?) We will let D be the point where this line intersects the largest of the semicircles; X and Y will indicate the points of intersection with the line segments AD and BD with the two smaller semicircles respectively (see Figure 2). Finally, let P be the point where XY and CD intersect. D X P Y ACBr 1 − r Figure 2 Problem 2. Now show that XY and CD are the same length, and that they bisect each other.
    [Show full text]
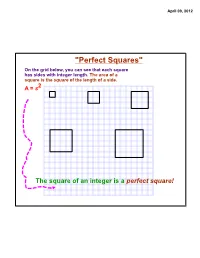
  • "Perfect Squares" on the Grid Below, You Can See That Each Square Has Sides with Integer Length
    April 09, 2012 "Perfect Squares" On the grid below, you can see that each square has sides with integer length. The area of a square is the square of the length of a side. A = s2 The square of an integer is a perfect square! April 09, 2012 Square Roots and Irrational Numbers The inverse of squaring a number is finding a square root. The square-root radical, , indicates the nonnegative square root of a number. The number underneath the square root (radical) sign is called the radicand. Ex: 16 = 121 = 49 = 144 = The square of an integer results in a perfect square. Since squaring a number is multiplying it by itself, there are two integer values that will result in the same perfect square: the positive integer and its opposite. 2 Ex: If x = (perfect square), solutions would be x and (-x)!! Ex: a2 = 25 5 and -5 would make this equation true! April 09, 2012 If an integer is NOT a perfect square, its square root is irrational!!! Remember that an irrational number has a decimal form that is non- terminating, non-repeating, and thus cannot be written as a fraction. For an integer that is not a perfect square, you can estimate its square root on a number line. Ex: 8 Since 22 = 4, and 32 = 9, 8 would fall between integers 2 and 3 on a number line. -2 -1 0 1 2 3 4 5 April 09, 2012 Approximate where √40 falls on the number line: Approximate where √192 falls on the number line: April 09, 2012 Topic Extension: Simplest Radical Form Simplify the radicand so that it has no more perfect-square factors.
    [Show full text]
  • Chapter 12, Lesson 1
    i8o Chapter 12, Lesson 1 Chapter 12, Lesson 1 •14. They are perpendicular. 15. The longest chord is always a diameter; so Set I (pages 486-487) its length doesn't depend on the location of According to Matthys Levy and Mario Salvador! the point. The length of the shortest chord in their book titled \Nhy Buildings Fall Down depends on how far away from the center (Norton, 1992), the Romans built semicircular the point is; the greater the distance, the arches of the type illustrated in exercises 1 through shorter the chord. 5 that spanned as much as 100 feet. These arches Theorem 56. were used in the bridges of 50,000 miles of roads that the Romans built all the way from Baghdad 16. Perpendicular lines form right angles. to London! • 17. Two points determine a line. The conclusions of exercises 13 through 15 are supported by the fact that a diameter of a circle is •18. All radii of a circle are equal. its longest chord and by symmetry considerations. 19. Reflexive. As the second chord rotates away from the diameter in either direction about the point of 20. HL. intersection, it becomes progressively shorter. 21. Corresponding parts of congruent triangles are equal. Roman Arch. •22. If a line divides a line segment into two 1. Radii. equal parts, it bisects the segment. •2. Chords. Theorem 57. •3. A diameter. 23. If a line bisects a line segment, it divides the 4. Isosceles. Each has two equal sides because segment into two equal parts. the radii of a circle are equal.
    [Show full text]
  • Lesson 20: Composite Area Problems
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 20 7•3 Lesson 20: Composite Area Problems Student Outcomes . Students find the area of regions in the coordinate plane with polygonal boundaries by decomposing the plane into triangles and quadrilaterals, including regions with polygonal holes. Students find composite areas of regions in the coordinate plane by decomposing the plane into familiar figures (triangles, quadrilaterals, circles, semicircles, and quarter circles). Lesson Notes In Lessons 17 through 20, students learned to find the areas of various regions, including quadrilaterals, triangles, circles, semicircles, and those plotted on coordinate planes. In this lesson, students use prior knowledge to use the sum and/or difference of the areas to find unknown composite areas. Classwork Example 1 (5 minutes) Scaffolding: For struggling students, display Example 1 posters around the room displaying the visuals and the Find the composite area of the shaded region. Use ퟑ. ퟏퟒ for 흅. formulas of the area of a circle, a triangle, and a quadrilateral for reference. Allow students to look at the problem and find the area independently before solving as a class. What information can we take from the image? Two circles are on the coordinate plane. The diameter of the larger circle is 6 units, and the diameter of MP.1 the smaller circle is 4 units. How do we know what the diameters of the circles are? We can count the units along the diameter of the circles, or we can subtract the coordinate points to find the length of the diameter. Lesson 20: Composite Area Problems 283 This work is derived from Eureka Math ™ and licensed by Great Minds.
    [Show full text]