DOCSLIB.ORG

Foundations of Geometry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Foundations of Geometry California State University, San Bernardino CSUSB ScholarWorks Theses Digitization Project John M. Pfau Library 2008 Foundations of geometry Lawrence Michael Clarke Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd-project Part of the Geometry and Topology Commons Recommended Citation Clarke, Lawrence Michael, "Foundations of geometry" (2008). Theses Digitization Project. 3419. https://scholarworks.lib.csusb.edu/etd-project/3419 This Thesis is brought to you for free and open access by the John M. Pfau Library at CSUSB ScholarWorks. It has been accepted for inclusion in Theses Digitization Project by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. Foundations of Geometry A Thesis Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degree Master of Arts in Mathematics by Lawrence Michael Clarke March 2008 Foundations of Geometry A Thesis Presented to the Faculty of California State University, San Bernardino by Lawrence Michael Clarke March 2008 Approved by: 3)?/08 Murran, Committee Chair Date _ ommi^yee Member Susan Addington, Committee Member 1 Peter Williams, Chair, Department of Mathematics Department of Mathematics iii Abstract In this paper, a brief introduction to the history, and development, of Euclidean Geometry will be followed by a biographical background of David Hilbert, highlighting significant events in his educational and professional life. In an attempt to add rigor to the presentation of Geometry, Hilbert defined concepts and presented five groups of axioms that were mutually independent yet compatible, including introducing axioms of congruence in order to present displacement. He originally presented this new material through a series of lectures during 1898-1899. Using this new presentation of geometry, he demonstrated an algebra of segments in accordance with the laws of arithmetic and showed that this was all possible without the axiom of continuity. In addition, Hilbert created new geometries in order to study Desargues’s Theorem as it relates to these axioms. iv Acknowledgements First, and foremost, I would like to thank God for the many people He put in my path to help me throughout the Master’s program, from classmates, professors and staff at the university to friends and associates that encouraged me along the way. Secondly, I would like to thank my wife and children for the incredibly patient support and understanding that they provided, knowing that the work that I was doing towards my Master’s degree was going to impinge on my commitments to them for a finite period of time. Finally, I would Eke to thank my committee members, each of which were very responsive and helpful throughout the lengthy process of this thesis paper, from the research and writing all the way through to the culmination of the final project. V Table of Contents Abstract iii Acknowledgements iv List of Figures vi 1 Classical Geometry: Euclid 1 2 David Hilbert’s Beginnings 4 3 Introduction to The Foundations of Geometry 9 4 The Five Groups of Axioms 10 5 Compatibility and Mutual Independence of the Axioms 15 6 Independence of the Axioms of Congruence and Continuity 19 7 The Theory of Proportion 23 8 An Algebra of Segments based upon Pascals Theorem 30 9 The Theory of Plane Areas 36 10 Desargues’s Theorem 41 11 Hilbert’s Conclusion 57 Bibliography 58 vi List of Figures 4.1 Axiom II-5: Intersection Between Line and Sides of Triangle ........ 11 5.1 Illustration of the Meaning of Axiom II-5....................................................... 16 5.2 Axiom III: Statement of Parallels....................................................................... 17 6.1 Axiom IV-3: Segments can be added................................................................. 20 7.1 Pascal’s Theory, of Proportion.............................................................................. 25 7.2 Cosine: Hilbert style.............................................................................................. 25 7.3 Angles are interchangeable.................................................................................... 26 7.4 Additional Labeling of Pascal’s Figure.............................................................. 27 7.5 Demonstrating Pascal’s Theorem...................... 28 7.6 Demonstrating Pascal’s Theorem II.................................................................... 29 8.1 Multiplication Defined Geometrically................................................................. 30 8.2 Commutative Law of Multiplication................................................................. 31 8.3 Associative Law of Multiplication....................................................................... 32 8.4 The First Distributive Law................................................................................. 32 8.5 Similar Triangles.................................................................................................... 33 8.6 General Case.......................................................................................................... 34 8.7 Co-ordinate System .............................................................................................. 35 9.1 Triangles of Equal Content ................................................................................. 37 9.2 Triangle with Equal Area to Parallelogram .................................................... 37 9.3 Equal Area versus Equal Content....................................................................... 38 9.4 Area of Triangle .................................................................................................... 39 9.5 Equal Area means Equal Content....................................................................... 40 10.1 Hilbert’s Geometry................................................................................................. 42 10.2 Redefining a Line.................................................................................................... 42 10.3 Congruence of Angles .......................................................................................... 43 10.4 Failure of Desargues’s Theorem.......................................................................... 43 10.5 Geometry Independent of Axioms of Congruence.......................................... 44 vii 10.6 Product of Segments............................................................................................. 45 10.7 Commutative Law of Addition.......................................................................... 46 10.8 Associative Law of Addition................................................................................. 47 10.9 Associative Law of Multiplication....................................................................... 47 lO.lODistributive Laws.................................................................................................... 49 10.11 Commutative Property of Addition.................................................................... 50 10.12The Second Statement of Distributive Property............................................. 51 10.13Straight Lines in Geometry................................................................................. 52 10.14Parallel Lines Create Equal Proportions.......................................................... 53 10.15Axiom II-5 Revisited.............................................................................................. 56 10.16Solutions to Linear Equation.............................................................................. 56 1 Chapter 1 Classical Geometry: Euclid Geometry is an ancient subject that has been around over 4000 years. Its roots are found in one form or another in nearly every human culture. The subject as we know it began in Mesopotamia, Egypt, India, and China. The Egyptians were most likely motivated by the annual flooding of the Nile, and its effect on farming. In their culture, Geometry was all about application, and often the numbers were arrived at through experimentation, observation, and trial and error. It appears that the work in the other aforementioned cultures actually was more advanced than the Egyptians. However, the ancient Greeks (800 B.C. to 150 B.C.) gave credit for the development of Geometry to the Egyptians that pre-dated them. The Greeks brought in a level of abstraction, logical deduction, and proof that had never existed before. This seems to have begun with Thales of Miletus around 600 B.C. and culminated in the works of Euclid 300 years later. Although it was widely known that Euclid had drawn from all his predecessors, nothing has been found from the earlier sources to support the level of rigor in the Math that was presented by Euclid around 300 B.C. He taught the essential features of Math in a much more general sense than had been done before. He laid the axiomatic foundation of theory, setting the standard that was used for over two thousand years. It was from his presentation of Geometry that the world learned how abstraction works. He defined terms, classified objects, and enforced a deductive presentation of theory. He presented material in such a way that a person with minimal mathematical training could benefit. And yet, he was also able to convey topics that are visible only to ’’the eyes of the mind,” as Plato would say. He did this in his presentation of irrational 2 and incommensurable magnitudes. His
Load more

Recommended publications
  • Circle Theorems
    Circle theorems A LEVEL LINKS Scheme of work: 2b. Circles – equation of a circle, geometric problems on a grid Key points • A chord is a straight line joining two points on the circumference of a circle. So AB is a chord. • A tangent is a straight line that touches the circumference of a circle at only one point. The angle between a tangent and the radius is 90°. • Two tangents on a circle that meet at a point outside the circle are equal in length. So AC = BC. • The angle in a semicircle is a right angle. So angle ABC = 90°. • When two angles are subtended by the same arc, the angle at the centre of a circle is twice the angle at the circumference. So angle AOB = 2 × angle ACB. • Angles subtended by the same arc at the circumference are equal. This means that angles in the same segment are equal. So angle ACB = angle ADB and angle CAD = angle CBD. • A cyclic quadrilateral is a quadrilateral with all four vertices on the circumference of a circle. Opposite angles in a cyclic quadrilateral total 180°. So x + y = 180° and p + q = 180°. • The angle between a tangent and chord is equal to the angle in the alternate segment, this is known as the alternate segment theorem. So angle BAT = angle ACB. Examples Example 1 Work out the size of each angle marked with a letter. Give reasons for your answers. Angle a = 360° − 92° 1 The angles in a full turn total 360°. = 268° as the angles in a full turn total 360°.
    [Show full text]
  • David Hilbert's Contributions to Logical Theory
    David Hilbert’s contributions to logical theory CURTIS FRANKS 1. A mathematician’s cast of mind Charles Sanders Peirce famously declared that “no two things could be more directly opposite than the cast of mind of the logician and that of the mathematician” (Peirce 1976, p. 595), and one who would take his word for it could only ascribe to David Hilbert that mindset opposed to the thought of his contemporaries, Frege, Gentzen, Godel,¨ Heyting, Łukasiewicz, and Skolem. They were the logicians par excellence of a generation that saw Hilbert seated at the helm of German mathematical research. Of Hilbert’s numerous scientific achievements, not one properly belongs to the domain of logic. In fact several of the great logical discoveries of the 20th century revealed deep errors in Hilbert’s intuitions—exemplifying, one might say, Peirce’s bald generalization. Yet to Peirce’s addendum that “[i]t is almost inconceivable that a man should be great in both ways” (Ibid.), Hilbert stands as perhaps history’s principle counter-example. It is to Hilbert that we owe the fundamental ideas and goals (indeed, even the name) of proof theory, the first systematic development and application of the methods (even if the field would be named only half a century later) of model theory, and the statement of the first definitive problem in recursion theory. And he did more. Beyond giving shape to the various sub-disciplines of modern logic, Hilbert brought them each under the umbrella of mainstream mathematical activity, so that for the first time in history teams of researchers shared a common sense of logic’s open problems, key concepts, and central techniques.
    [Show full text]
  • Einstein and Hilbert: the Creation of General Relativity
    EINSTEIN AND HILBERT: THE CREATION OF GENERAL RELATIVITY ∗ Ivan T. Todorov Institut f¨ur Theoretische Physik, Universit¨at G¨ottingen, Friedrich-Hund-Platz 1 D-37077 G¨ottingen, Germany; e-mail: [email protected] and Institute for Nuclear Research and Nuclear Energy, Bulgarian Academy of Sciences Tsarigradsko Chaussee 72, BG-1784 Sofia, Bulgaria;∗∗e-mail: [email protected] ABSTRACT It took eight years after Einstein announced the basic physical ideas behind the relativistic gravity theory before the proper mathematical formulation of general relativity was mastered. The efforts of the greatest physicist and of the greatest mathematician of the time were involved and reached a breathtaking concentration during the last month of the work. Recent controversy, raised by a much publicized 1997 reading of Hilbert’s proof- sheets of his article of November 1915, is also discussed. arXiv:physics/0504179v1 [physics.hist-ph] 25 Apr 2005 ∗ Expanded version of a Colloquium lecture held at the International Centre for Theoretical Physics, Trieste, 9 December 1992 and (updated) at the International University Bremen, 15 March 2005. ∗∗ Permanent address. Introduction Since the supergravity fashion and especially since the birth of superstrings a new science emerged which may be called “high energy mathematical physics”. One fad changes the other each going further away from accessible experiments and into mathe- matical models, ending up, at best, with the solution of an interesting problem in pure mathematics. The realization of the grand original design seems to be, decades later, nowhere in sight. For quite some time, though, the temptation for mathematical physi- cists (including leading mathematicians) was hard to resist.
    [Show full text]
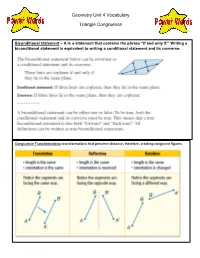
  • Geometry Unit 4 Vocabulary Triangle Congruence
    Geometry Unit 4 Vocabulary Triangle Congruence Biconditional statement – A is a statement that contains the phrase “if and only if.” Writing a biconditional statement is equivalent to writing a conditional statement and its converse. Congruence Transformations–transformations that preserve distance, therefore, creating congruent figures Congruence – the same shape and the same size Corresponding Parts of Congruent Triangles are Congruent CPCTC – the angle made by two lines with a common vertex. (When two lines meet at a common point Included angle (vertex) the angle between them is called the included angle. The two lines define the angle.) Included side – the common side of two legs. (Usually found in triangles and other polygons, the included side is the one that links two angles together. Think of it as being “included” between 2 angles. Overlapping triangles – triangles lying on top of one another sharing some but not all sides. Theorems AAS Congruence Theorem – Triangles are congruent if two pairs of corresponding angles and a pair of opposite sides are equal in both triangles. ASA Congruence Theorem -Triangles are congruent if any two angles and their included side are equal in both triangles. SAS Congruence Theorem -Triangles are congruent if any pair of corresponding sides and their included angles are equal in both triangles. SAS SSS Congruence Theorem -Triangles are congruent if all three sides in one triangle are congruent to the corresponding sides in the other. Special congruence theorem for RIGHT TRIANGLES! .
    [Show full text]
  • A Congruence Problem for Polyhedra
    A congruence problem for polyhedra Alexander Borisov, Mark Dickinson, Stuart Hastings April 18, 2007 Abstract It is well known that to determine a triangle up to congruence requires 3 measurements: three sides, two sides and the included angle, or one side and two angles. We consider various generalizations of this fact to two and three dimensions. In particular we consider the following question: given a convex polyhedron P , how many measurements are required to determine P up to congruence? We show that in general the answer is that the number of measurements required is equal to the number of edges of the polyhedron. However, for many polyhedra fewer measurements suffice; in the case of the cube we show that nine carefully chosen measurements are enough. We also prove a number of analogous results for planar polygons. In particular we describe a variety of quadrilaterals, including all rhombi and all rectangles, that can be determined up to congruence with only four measurements, and we prove the existence of n-gons requiring only n measurements. Finally, we show that one cannot do better: for any ordered set of n distinct points in the plane one needs at least n measurements to determine this set up to congruence. An appendix by David Allwright shows that the set of twelve face-diagonals of the cube fails to determine the cube up to conjugacy. Allwright gives a classification of all hexahedra with all face- diagonals of equal length. 1 Introduction We discuss a class of problems about the congruence or similarity of three dimensional polyhedra.
    [Show full text]
  • 20. Geometry of the Circle (SC)
    20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord.
    [Show full text]
  • Understand the Principles and Properties of Axiomatic (Synthetic
    Michael Bonomi Understand the principles and properties of axiomatic (synthetic) geometries (0016) Euclidean Geometry: To understand this part of the CST I decided to start off with the geometry we know the most and that is Euclidean: − Euclidean geometry is a geometry that is based on axioms and postulates − Axioms are accepted assumptions without proofs − In Euclidean geometry there are 5 axioms which the rest of geometry is based on − Everybody had no problems with them except for the 5 axiom the parallel postulate − This axiom was that there is only one unique line through a point that is parallel to another line − Most of the geometry can be proven without the parallel postulate − If you do not assume this postulate, then you can only prove that the angle measurements of right triangle are ≤ 180° Hyperbolic Geometry: − We will look at the Poincare model − This model consists of points on the interior of a circle with a radius of one − The lines consist of arcs and intersect our circle at 90° − Angles are defined by angles between the tangent lines drawn between the curves at the point of intersection − If two lines do not intersect within the circle, then they are parallel − Two points on a line in hyperbolic geometry is a line segment − The angle measure of a triangle in hyperbolic geometry < 180° Projective Geometry: − This is the geometry that deals with projecting images from one plane to another this can be like projecting a shadow − This picture shows the basics of Projective geometry − The geometry does not preserve length
    [Show full text]
  • Geometry Course Outline
    GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid
    [Show full text]
  • Old and New Results in the Foundations of Elementary Plane Euclidean and Non-Euclidean Geometries Marvin Jay Greenberg
    Old and New Results in the Foundations of Elementary Plane Euclidean and Non-Euclidean Geometries Marvin Jay Greenberg By “elementary” plane geometry I mean the geometry of lines and circles—straight- edge and compass constructions—in both Euclidean and non-Euclidean planes. An axiomatic description of it is in Sections 1.1, 1.2, and 1.6. This survey highlights some foundational history and some interesting recent discoveries that deserve to be better known, such as the hierarchies of axiom systems, Aristotle’s axiom as a “missing link,” Bolyai’s discovery—proved and generalized by William Jagy—of the relationship of “circle-squaring” in a hyperbolic plane to Fermat primes, the undecidability, incom- pleteness, and consistency of elementary Euclidean geometry, and much more. A main theme is what Hilbert called “the purity of methods of proof,” exemplified in his and his early twentieth century successors’ works on foundations of geometry. 1. AXIOMATIC DEVELOPMENT 1.0. Viewpoint. Euclid’s Elements was the first axiomatic presentation of mathemat- ics, based on his five postulates plus his “common notions.” It wasn’t until the end of the nineteenth century that rigorous revisions of Euclid’s axiomatics were presented, filling in the many gaps in his definitions and proofs. The revision with the great- est influence was that by David Hilbert starting in 1899, which will be discussed below. Hilbert not only made Euclid’s geometry rigorous, he investigated the min- imal assumptions needed to prove Euclid’s results, he showed the independence of some of his own axioms from the others, he presented unusual models to show certain statements unprovable from others, and in subsequent editions he explored in his ap- pendices many other interesting topics, including his foundation for plane hyperbolic geometry without bringing in real numbers.
    [Show full text]
  • Mechanism, Mentalism, and Metamathematics Synthese Library
    MECHANISM, MENTALISM, AND METAMATHEMATICS SYNTHESE LIBRARY STUDIES IN EPISTEMOLOGY, LOGIC, METHODOLOGY, AND PHILOSOPHY OF SCIENCE Managing Editor: JAAKKO HINTIKKA, Florida State University Editors: ROBER T S. COHEN, Boston University DONALD DAVIDSON, University o/Chicago GABRIEL NUCHELMANS, University 0/ Leyden WESLEY C. SALMON, University 0/ Arizona VOLUME 137 JUDSON CHAMBERS WEBB Boston University. Dept. 0/ Philosophy. Boston. Mass .• U.S.A. MECHANISM, MENT ALISM, AND MET AMA THEMA TICS An Essay on Finitism i Springer-Science+Business Media, B.V. Library of Congress Cataloging in Publication Data Webb, Judson Chambers, 1936- CII:J Mechanism, mentalism, and metamathematics. (Synthese library; v. 137) Bibliography: p. Includes indexes. 1. Metamathematics. I. Title. QA9.8.w4 510: 1 79-27819 ISBN 978-90-481-8357-9 ISBN 978-94-015-7653-6 (eBook) DOl 10.1007/978-94-015-7653-6 All Rights Reserved Copyright © 1980 by Springer Science+Business Media Dordrecht Originally published by D. Reidel Publishing Company, Dordrecht, Holland in 1980. Softcover reprint of the hardcover 1st edition 1980 No part of the material protected by this copyright notice may be reproduced or utilized in any form or by any means, electronic or mechanical, including photocopying, recording or by any informational storage and retrieval system, without written permission from the copyright owner TABLE OF CONTENTS PREFACE vii INTRODUCTION ix CHAPTER I / MECHANISM: SOME HISTORICAL NOTES I. Machines and Demons 2. Machines and Men 17 3. Machines, Arithmetic, and Logic 22 CHAPTER II / MIND, NUMBER, AND THE INFINITE 33 I. The Obligations of Infinity 33 2. Mind and Philosophy of Number 40 3. Dedekind's Theory of Arithmetic 46 4.
    [Show full text]
  • Georg Cantor English Version
    GEORG CANTOR (March 3, 1845 – January 6, 1918) by HEINZ KLAUS STRICK, Germany There is hardly another mathematician whose reputation among his contemporary colleagues reflected such a wide disparity of opinion: for some, GEORG FERDINAND LUDWIG PHILIPP CANTOR was a corruptor of youth (KRONECKER), while for others, he was an exceptionally gifted mathematical researcher (DAVID HILBERT 1925: Let no one be allowed to drive us from the paradise that CANTOR created for us.) GEORG CANTOR’s father was a successful merchant and stockbroker in St. Petersburg, where he lived with his family, which included six children, in the large German colony until he was forced by ill health to move to the milder climate of Germany. In Russia, GEORG was instructed by private tutors. He then attended secondary schools in Wiesbaden and Darmstadt. After he had completed his schooling with excellent grades, particularly in mathematics, his father acceded to his son’s request to pursue mathematical studies in Zurich. GEORG CANTOR could equally well have chosen a career as a violinist, in which case he would have continued the tradition of his two grandmothers, both of whom were active as respected professional musicians in St. Petersburg. When in 1863 his father died, CANTOR transferred to Berlin, where he attended lectures by KARL WEIERSTRASS, ERNST EDUARD KUMMER, and LEOPOLD KRONECKER. On completing his doctorate in 1867 with a dissertation on a topic in number theory, CANTOR did not obtain a permanent academic position. He taught for a while at a girls’ school and at an institution for training teachers, all the while working on his habilitation thesis, which led to a teaching position at the university in Halle.
    [Show full text]
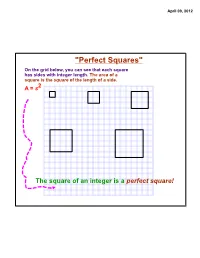
  • "Perfect Squares" on the Grid Below, You Can See That Each Square Has Sides with Integer Length
    April 09, 2012 "Perfect Squares" On the grid below, you can see that each square has sides with integer length. The area of a square is the square of the length of a side. A = s2 The square of an integer is a perfect square! April 09, 2012 Square Roots and Irrational Numbers The inverse of squaring a number is finding a square root. The square-root radical, , indicates the nonnegative square root of a number. The number underneath the square root (radical) sign is called the radicand. Ex: 16 = 121 = 49 = 144 = The square of an integer results in a perfect square. Since squaring a number is multiplying it by itself, there are two integer values that will result in the same perfect square: the positive integer and its opposite. 2 Ex: If x = (perfect square), solutions would be x and (-x)!! Ex: a2 = 25 5 and -5 would make this equation true! April 09, 2012 If an integer is NOT a perfect square, its square root is irrational!!! Remember that an irrational number has a decimal form that is non- terminating, non-repeating, and thus cannot be written as a fraction. For an integer that is not a perfect square, you can estimate its square root on a number line. Ex: 8 Since 22 = 4, and 32 = 9, 8 would fall between integers 2 and 3 on a number line. -2 -1 0 1 2 3 4 5 April 09, 2012 Approximate where √40 falls on the number line: Approximate where √192 falls on the number line: April 09, 2012 Topic Extension: Simplest Radical Form Simplify the radicand so that it has no more perfect-square factors.
    [Show full text]