A Congruence Problem for Polyhedra
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Applying the Polygon Angle
POLYGONS 8.1.1 – 8.1.5 After studying triangles and quadrilaterals, students now extend their study to all polygons. A polygon is a closed, two-dimensional figure made of three or more non- intersecting straight line segments connected end-to-end. Using the fact that the sum of the measures of the angles in a triangle is 180°, students learn a method to determine the sum of the measures of the interior angles of any polygon. Next they explore the sum of the measures of the exterior angles of a polygon. Finally they use the information about the angles of polygons along with their Triangle Toolkits to find the areas of regular polygons. See the Math Notes boxes in Lessons 8.1.1, 8.1.5, and 8.3.1. Example 1 4x + 7 3x + 1 x + 1 The figure at right is a hexagon. What is the sum of the measures of the interior angles of a hexagon? Explain how you know. Then write an equation and solve for x. 2x 3x – 5 5x – 4 One way to find the sum of the interior angles of the 9 hexagon is to divide the figure into triangles. There are 11 several different ways to do this, but keep in mind that we 8 are trying to add the interior angles at the vertices. One 6 12 way to divide the hexagon into triangles is to draw in all of 10 the diagonals from a single vertex, as shown at right. 7 Doing this forms four triangles, each with angle measures 5 4 3 1 summing to 180°. -
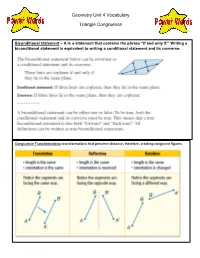
Geometry Unit 4 Vocabulary Triangle Congruence
Geometry Unit 4 Vocabulary Triangle Congruence Biconditional statement – A is a statement that contains the phrase “if and only if.” Writing a biconditional statement is equivalent to writing a conditional statement and its converse. Congruence Transformations–transformations that preserve distance, therefore, creating congruent figures Congruence – the same shape and the same size Corresponding Parts of Congruent Triangles are Congruent CPCTC – the angle made by two lines with a common vertex. (When two lines meet at a common point Included angle (vertex) the angle between them is called the included angle. The two lines define the angle.) Included side – the common side of two legs. (Usually found in triangles and other polygons, the included side is the one that links two angles together. Think of it as being “included” between 2 angles. Overlapping triangles – triangles lying on top of one another sharing some but not all sides. Theorems AAS Congruence Theorem – Triangles are congruent if two pairs of corresponding angles and a pair of opposite sides are equal in both triangles. ASA Congruence Theorem -Triangles are congruent if any two angles and their included side are equal in both triangles. SAS Congruence Theorem -Triangles are congruent if any pair of corresponding sides and their included angles are equal in both triangles. SAS SSS Congruence Theorem -Triangles are congruent if all three sides in one triangle are congruent to the corresponding sides in the other. Special congruence theorem for RIGHT TRIANGLES! . -

Graphing a Circle and a Polar Equation 13 Graphing Calculator Lab (Use with Lessons 91, 96)
SSM_A2_NLB_SBK_Lab13.inddM_A2_NLB_SBK_Lab13.indd PagePage 638638 6/12/086/12/08 2:42:452:42:45 AMAM useruser //Volumes/ju110/HCAC061/SM_A2_SBK_indd%0/SM_A2_NL_SBK_LAB/SM_A2_Lab_13Volumes/ju110/HCAC061/SM_A2_SBK_indd%0/SM_A2_NL_SBK_LAB/SM_A2_Lab_13 LAB Graphing a Circle and a Polar Equation 13 Graphing Calculator Lab (Use with Lessons 91, 96) Graphing a Circle in Function Mode 2 2 Graphing 1. Enter the equation of the circle (x - 3) + (y - 5) = 21 as the two Calculator functions, y = ± √21 - (x - 3)2 + 5. Refer to Calculator Lab 1 a. Press to access the Y= equation on page 19 for graphing a function. editor screen. 2 b. Type √21 - (x - 3) + 5 into Y1 2 and - √21 - (x - 3) + 5 into Y2 c. Press to graph the functions. d. Use the or button to adjust the window. The graph will have a more circular shape using 5 rather than 6. Graphing a Polar Equation 2. Change the mode of the calculator to polar mode. a. Press .Press two times to highlight RADIAN, and then press enter. b. Press to FUNC, and then two times to highlight POL, and then press . c. Press two more times to SEQUENTIAL, press to highlight SIMUL, and then press . d. To exit the MODE menu, press . 3. Enter the equation of the circle (x - 3)2 + (y - 5)2 = 34 as the polar equation r = 6 cos θ - 10 sin θ. a. Press to access the r1 = equation editor screen. b. Type in 6 cos θ - 10 sin θ into r1 by pressing Online Connection www.SaxonMathResources.com . 638 Saxon Algebra 2 SSM_A2_NLB_SBK_Lab13.inddM_A2_NLB_SBK_Lab13.indd PagePage 639639 6/13/086/13/08 3:45:473:45:47 PMPM User-17User-17 //Volumes/ju110/HCAC061/SM_A2_SBK_indd%0/SM_A2_NL_SBK_LAB/SM_A2_Lab_13Volumes/ju110/HCAC061/SM_A2_SBK_indd%0/SM_A2_NL_SBK_LAB/SM_A2_Lab_13 Graphing 4. -

Understand the Principles and Properties of Axiomatic (Synthetic
Michael Bonomi Understand the principles and properties of axiomatic (synthetic) geometries (0016) Euclidean Geometry: To understand this part of the CST I decided to start off with the geometry we know the most and that is Euclidean: − Euclidean geometry is a geometry that is based on axioms and postulates − Axioms are accepted assumptions without proofs − In Euclidean geometry there are 5 axioms which the rest of geometry is based on − Everybody had no problems with them except for the 5 axiom the parallel postulate − This axiom was that there is only one unique line through a point that is parallel to another line − Most of the geometry can be proven without the parallel postulate − If you do not assume this postulate, then you can only prove that the angle measurements of right triangle are ≤ 180° Hyperbolic Geometry: − We will look at the Poincare model − This model consists of points on the interior of a circle with a radius of one − The lines consist of arcs and intersect our circle at 90° − Angles are defined by angles between the tangent lines drawn between the curves at the point of intersection − If two lines do not intersect within the circle, then they are parallel − Two points on a line in hyperbolic geometry is a line segment − The angle measure of a triangle in hyperbolic geometry < 180° Projective Geometry: − This is the geometry that deals with projecting images from one plane to another this can be like projecting a shadow − This picture shows the basics of Projective geometry − The geometry does not preserve length -

Geometrygeometry
Park Forest Math Team Meet #3 GeometryGeometry Self-study Packet Problem Categories for this Meet: 1. Mystery: Problem solving 2. Geometry: Angle measures in plane figures including supplements and complements 3. Number Theory: Divisibility rules, factors, primes, composites 4. Arithmetic: Order of operations; mean, median, mode; rounding; statistics 5. Algebra: Simplifying and evaluating expressions; solving equations with 1 unknown including identities Important Information you need to know about GEOMETRY… Properties of Polygons, Pythagorean Theorem Formulas for Polygons where n means the number of sides: • Exterior Angle Measurement of a Regular Polygon: 360÷n • Sum of Interior Angles: 180(n – 2) • Interior Angle Measurement of a regular polygon: • An interior angle and an exterior angle of a regular polygon always add up to 180° Interior angle Exterior angle Diagonals of a Polygon where n stands for the number of vertices (which is equal to the number of sides): • • A diagonal is a segment that connects one vertex of a polygon to another vertex that is not directly next to it. The dashed lines represent some of the diagonals of this pentagon. Pythagorean Theorem • a2 + b2 = c2 • a and b are the legs of the triangle and c is the hypotenuse (the side opposite the right angle) c a b • Common Right triangles are ones with sides 3, 4, 5, with sides 5, 12, 13, with sides 7, 24, 25, and multiples thereof—Memorize these! Category 2 50th anniversary edition Geometry 26 Y Meet #3 - January, 2014 W 1) How many cm long is segment 6 XY ? All measurements are in centimeters (cm). -

Geometry Course Outline
GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid -

Fundamental Principles Governing the Patterning of Polyhedra
FUNDAMENTAL PRINCIPLES GOVERNING THE PATTERNING OF POLYHEDRA B.G. Thomas and M.A. Hann School of Design, University of Leeds, Leeds LS2 9JT, UK. [email protected] ABSTRACT: This paper is concerned with the regular patterning (or tiling) of the five regular polyhedra (known as the Platonic solids). The symmetries of the seventeen classes of regularly repeating patterns are considered, and those pattern classes that are capable of tiling each solid are identified. Based largely on considering the symmetry characteristics of both the pattern and the solid, a first step is made towards generating a series of rules governing the regular tiling of three-dimensional objects. Key words: symmetry, tilings, polyhedra 1. INTRODUCTION A polyhedron has been defined by Coxeter as “a finite, connected set of plane polygons, such that every side of each polygon belongs also to just one other polygon, with the provision that the polygons surrounding each vertex form a single circuit” (Coxeter, 1948, p.4). The polygons that join to form polyhedra are called faces, 1 these faces meet at edges, and edges come together at vertices. The polyhedron forms a single closed surface, dissecting space into two regions, the interior, which is finite, and the exterior that is infinite (Coxeter, 1948, p.5). The regularity of polyhedra involves regular faces, equally surrounded vertices and equal solid angles (Coxeter, 1948, p.16). Under these conditions, there are nine regular polyhedra, five being the convex Platonic solids and four being the concave Kepler-Poinsot solids. The term regular polyhedron is often used to refer only to the Platonic solids (Cromwell, 1997, p.53). -

The Crystal Forms of Diamond and Their Significance
THE CRYSTAL FORMS OF DIAMOND AND THEIR SIGNIFICANCE BY SIR C. V. RAMAN AND S. RAMASESHAN (From the Department of Physics, Indian Institute of Science, Bangalore) Received for publication, June 4, 1946 CONTENTS 1. Introductory Statement. 2. General Descriptive Characters. 3~ Some Theoretical Considerations. 4. Geometric Preliminaries. 5. The Configuration of the Edges. 6. The Crystal Symmetry of Diamond. 7. Classification of the Crystal Forros. 8. The Haidinger Diamond. 9. The Triangular Twins. 10. Some Descriptive Notes. 11. The Allo- tropic Modifications of Diamond. 12. Summary. References. Plates. 1. ~NTRODUCTORY STATEMENT THE" crystallography of diamond presents problems of peculiar interest and difficulty. The material as found is usually in the form of complete crystals bounded on all sides by their natural faces, but strangely enough, these faces generally exhibit a marked curvature. The diamonds found in the State of Panna in Central India, for example, are invariably of this kind. Other diamondsJas for example a group of specimens recently acquired for our studies ffom Hyderabad (Deccan)--show both plane and curved faces in combination. Even those diamonds which at first sight seem to resemble the standard forms of geometric crystallography, such as the rhombic dodeca- hedron or the octahedron, are found on scrutiny to exhibit features which preclude such an identification. This is the case, for example, witb. the South African diamonds presented to us for the purpose of these studŸ by the De Beers Mining Corporation of Kimberley. From these facts it is evident that the crystallography of diamond stands in a class by itself apart from that of other substances and needs to be approached from a distinctive stand- point. -

Foundations of Geometry
California State University, San Bernardino CSUSB ScholarWorks Theses Digitization Project John M. Pfau Library 2008 Foundations of geometry Lawrence Michael Clarke Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd-project Part of the Geometry and Topology Commons Recommended Citation Clarke, Lawrence Michael, "Foundations of geometry" (2008). Theses Digitization Project. 3419. https://scholarworks.lib.csusb.edu/etd-project/3419 This Thesis is brought to you for free and open access by the John M. Pfau Library at CSUSB ScholarWorks. It has been accepted for inclusion in Theses Digitization Project by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. Foundations of Geometry A Thesis Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degree Master of Arts in Mathematics by Lawrence Michael Clarke March 2008 Foundations of Geometry A Thesis Presented to the Faculty of California State University, San Bernardino by Lawrence Michael Clarke March 2008 Approved by: 3)?/08 Murran, Committee Chair Date _ ommi^yee Member Susan Addington, Committee Member 1 Peter Williams, Chair, Department of Mathematics Department of Mathematics iii Abstract In this paper, a brief introduction to the history, and development, of Euclidean Geometry will be followed by a biographical background of David Hilbert, highlighting significant events in his educational and professional life. In an attempt to add rigor to the presentation of Geometry, Hilbert defined concepts and presented five groups of axioms that were mutually independent yet compatible, including introducing axioms of congruence in order to present displacement. -

∆ Congruence & Similarity
www.MathEducationPage.org Henri Picciotto Triangle Congruence and Similarity A Common-Core-Compatible Approach Henri Picciotto The Common Core State Standards for Mathematics (CCSSM) include a fundamental change in the geometry program in grades 8 to 10: geometric transformations, not congruence and similarity postulates, are to constitute the logical foundation of geometry at this level. This paper proposes an approach to triangle congruence and similarity that is compatible with this new vision. Transformational Geometry and the Common Core From the CCSSM1: The concepts of congruence, similarity, and symmetry can be understood from the perspective of geometric transformation. Fundamental are the rigid motions: translations, rotations, reflections, and combinations of these, all of which are here assumed to preserve distance and angles (and therefore shapes generally). Reflections and rotations each explain a particular type of symmetry, and the symmetries of an object offer insight into its attributes—as when the reflective symmetry of an isosceles triangle assures that its base angles are congruent. In the approach taken here, two geometric figures are defined to be congruent if there is a sequence of rigid motions that carries one onto the other. This is the principle of superposition. For triangles, congruence means the equality of all corresponding pairs of sides and all corresponding pairs of angles. During the middle grades, through experiences drawing triangles from given conditions, students notice ways to specify enough measures in a triangle to ensure that all triangles drawn with those measures are congruent. Once these triangle congruence criteria (ASA, SAS, and SSS) are established using rigid motions, they can be used to prove theorems about triangles, quadrilaterals, and other geometric figures. -

Congruence Theory Explained
UC Irvine CSD Working Papers Title Congruence Theory Explained Permalink https://escholarship.org/uc/item/2wb616g6 Author Eckstein, Harry Publication Date 1997-07-15 eScholarship.org Powered by the California Digital Library University of California CSD Center for the Study of Democracy An Organized Research Unit University of California, Irvine www.democ.uci.edu The authors of the essays that constitute this book have made a theory I first developed in the 1960s its unifying thread. This theory may be called "congruence theory." It has been elaborated several times, in numerous ways, since its first statement, but has not changed in essentials.1 I do not want to explain and justify the theory in all its ramifications here; for this, readers can consult the publications cited in the references. I do want to explain it sufficiently to clarify essentials. The Core of Congruence Theory Every theory has at its "core" certain fundamental hypotheses. These can be used as if they were "axioms" from which theorems (further hypotheses) may be deduced; the theory may then be tested directly through the axioms or indirectly through the theorems. A good deal of auxiliary theoretical matter is generally associated with the core-hypotheses, usually to make them amenable to appropriate empirical inquiry. These auxiliary matters are subsidiary to the core- postulates of a theory, but they are necessary for doing work with it and generally imply hypotheses themselves.2 Congruence theory has such an underlying core, with which a great deal of auxiliary material has become associated; the more important of these auxiliary ideas will be discussed later. -

Tetrahedral Decompositions of Hexahedral Meshes
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Europ. J. Combinatorics (1989) 10, 435-443 Tetrahedral Decompositions of Hexahedral Meshes DEREK HACON AND CARLOS TOMEI A hexahedral mesh is a partition of a region in 3-space 1R3 into (not necessarily regular) hexahedra which fit together face to face. We are concerned here with the question of how the hexahedra may be decomposed into tetrahedra without introducing any new vertices. We consider two possible decompositions, in which each hexahedron breaks into five or six tetrahedra in a prescribed fashion. In both cases, we obtain simple verifiable criteria for the existence of a decomposition, by making use of elementary facts of graph theory and algebraic. topology. 1. INTRODUcnON A hexahedral mesh is a partition of a region in 3-space ~3 into (not necessarily regular) hexahedra which fit together face to face. We are concerned here with the question of how the hexahedra may be decomposed into tetrahedra without introduc ing any new vertices. There is one well known [1] way of decomposing a hexahedral mesh into non-overlapping tetrahedra which always works. Start by labelling the vertices 1,2,3, .... Then divide each face into two triangles by the diagonal containing the first vertex of the face. Next consider a hexahedron H with first vertex V. The three faces of H not containing V have already been divided up into a total of six triangles, so take each of these to be the base of a tetrahedron with apex V.