DOCSLIB.ORG

Introduction Introducing Geosolids

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Introduction Introducing Geosolids INTRODUCTION Learning About®... GeoSolidsTM is a resource providing hands-on activities and ideas that allow you, the teacher, to lead students in an active exploration of the world of mathematics. The activities presented involve students in the process of exploring abstract concepts through the use of manipulatives. Students are encouraged to think critically, plan strategy, and share conclusions. Learning About ... GeoSolids emphasizes— n communication n exploration n problem solving n analysis The Basic GeoSolids Set consists of the following six shapes: cube, cylinder, sphere, cone, triangular prism, and pyramid. The twelve-piece GeoSolids Set consists of a cube, a cone, two rectangular prisms (one square), two cylinders, a hemisphere, a sphere, a pyramid, a triangular prism, a hexagonal prism, and an octagonal prism. GeoSolids can be used to— n explore which flat shapes are part of the solid figures n identify attributes such as the number of faces, corners, and edges n discover which shapes can slide, roll, or stack Exploring with GeoSolids Students at all grade levels should be allowed time to freely explore and experiment with GeoSolids before guided activities begin. INTRODUCING GEOSOLIDS Group Size: Whole Class Procedure: Display the set of GeoSolids. Note: Teachers of kindergarten through grade 2 may wish to initially display only two or three geometric solids–cube, cylinder, and sphere. The prism, cone, and pyramid may be introduced at a later date. Hold up the sphere. Describe and name the shape. Use clues about its attributes. n This shape is a sphere. (Primary students may identify this shape as a ball.) n The sphere is round and it can roll. 2 Invite students to identify classroom objects that have the same shape. [ball, globe, etc.] Hold up the cube. Describe and name the shape. Use clues about its attributes. n This shape is a cube. (Primary students may identify this shape as a box.) n The cube has flat sides and corners. It cannot roll. Challenge students to identify classroom or household objects that have the same shape. Hold up the cylinder. Describe and name the shape. Use clues about its attributes. n This shape is a cylinder. (Primary students may identify this shape as a can.) n The cylinder has 2 flat sides. It has no corners. The cylinder can roll. Challenge students to identify classroom or household objects that have the same shape. Continue this activity for the cone, pyramid, and triangular prism. Additional information regarding the set of twelve GeoSolids: Hold up the sphere and hemisphere. Name the shapes and describe them, using clues about their attributes. n This shape is a sphere. The sphere is round and it can roll. n This shape is a hemisphere. The hemisphere has one flat side. Write the prefix “hemi” on the chalkboard. Explain that this prefix indicates half of something. n How are the sphere and hemisphere alike or related? [Answers will vary. The hemisphere is half of the whole sphere.] Hold up the two cylinders. Name and describe the shape. Use clues about their attributes. n These shapes are cylinders. n Each cylinder has two flat sides. The cylinder has no corners. The top and bottom of the cylinder are circles. A cylinder can roll. n How are the cylinders alike? Different? [Answers will vary. Both have the same shape. One cylinder is tall and narrow. The other cylinder is short and wide.] Continue this activity for the cube, cone, and pyramid. Describe and name the shapes. Use clues about their attributes. Hold up the two rectangular prisms. Name and describe the shapes. n These shapes are rectangular prisms. Each prism has flat sides. The sides meet to form corners. A rectangular prism cannot roll. n How are the rectangular prisms alike? different? [Answers will vary. Both have the same shape. One prism is tall and narrow. The other prism is short and wide.] Hold up the triangular prism. Name and describe the shape. Use clues about its attributes. 3 n This shape is a triangular prism. It has flat sides. The sides meet to form corners. It cannot roll. Write the prefix “tri” on the chalkboard. Challenge students to define the prefix. “Tri” means three. n Why is the prefix “tri” meaningful in identifying this prism? [The two flat ends of this prism are in the form of a three-sided shape or triangle.] Hold up the hexagonal prism. Name and describe the shape. n This shape is a hexagonal prism. It has flat sides. It does not roll smoothly. Write the prefix “hexa” on the chalkboard. Explain that this prefix means six. n Why is the prefix “hexa” meaningful in identifying this prism? [The two ends of this prism are in the form of a six-sided shape or hexagon.] Hold up the octagonal prism. Name and describe the shape. n This shape is an octagonal prism. It has flat sides. The sides meet to form corners. This prism does not roll smoothly. Write the prefix “octa” on the chalkboard. Explain that this prefix means eight. n Why is this prefix meaningful in identifying this prism? [The two ends of this prism are in the form of an eight-sided shape or octagon.] SHAPE MATCH Challenge students to identify classroom or household objects that have the same shape as the GeoSolids. Group Size: Whole Class or Small Groups Materials: GeoSolids; classroom or household objects in the shapes of the GeoSolids — cans, chalk, paper towel tubes, boxes, number cubes, paper cones, etc; large paper bag Procedure: Hold up each GeoSolids shape. Identify the solid by name. Invite students to describe the shape and attributes of the solid. After each solid is identified and described, place it in the paper bag. Hold up a cardboard tube (paper towel type). Ask a student volunteer to describe the attributes of the tube. [It can roll. It is round and long.] Invite another student to reach into the paper bag containing the GeoSolids. Using only the sense of touch, the student is to find the matching solid. [cylinder] Have students take turns matching common objects to the GeoSolids in the paper bag. Encourage students to describe the attributes of the common object and the GeoSolids shape that make a match. 4 CORNERS AND SIDES Group Size: Small Groups Procedure: Provide a set of GeoSolids for each group of students. n What do you think of when you hear the words corner and side? [Answers will vary.] Provide an opportunity for each group of students to closely examine the GeoSolids. Encourage students to group the solids according to similarities. Invite a volunteer from each group to present the findings of the group. n How are the GeoSolids shapes alike and how are they different? [Answers will vary.] n Which shapes have flat sides? [For the set of six — cube, triangular prism, cylinder, cone, and pyramid. For the set of twelve — cube, rectangular prism, cylinder, cone, pyramid, hemisphere, hexagonal prism, octagonal prism, and triangular prism.] n Which shapes have corners? [For the set of six — cube, triangular prism, and pyramid. For the set of twelve — cube, rectangular prism, pyramid, hexagonal prism, octagonal prism, triangular prism.] Create the following chart on the chalkboard. List the solids contained in your set. Solid Corners Flat Sides cube [8] [6] triangular prism [6] [5] cylinder [0] [2] cone [0] [1] pyramid [5] [5] sphere [0] [0] hemisphere [0] [1] rectangular prism [8] [6] hexagonal prism [12] [8] octagonal prism [16] [10] Hold up each GeoSolids shape individually. Ask students to describe the solid, making note of the number of corners and flat sides. Fill in the chalkboard chart. Encourage students to name a classroom or everyday object that is an example of each solid. 5 ROLL AND STACK Group Size: Small Groups Procedure: Provide a set of six GeoSolids shapes for each group of students– cube, sphere, triangular prism, cylinder, cone, and pyramid. Allow students a few minutes to freely explore the solids. Encourage students to move the shapes, feel them, and discover how the shapes are alike and different. n How can we tell if a solid can be stacked? [Students may employ various strategies. A solid needs to have at least two parallel flat sides in order to stack.] n Which of the GeoSolids can be stacked? [cube, triangular prism, cylinder] n Which of the GeoSolids can roll? [cylinder, sphere, cone] n Why do these solids roll? [They have curved surfaces.] Create the following chart on the chalkboard. Call on student volunteers to demonstrate the stacking and rolling attributes of each GeoSolids shape. Solid Stack Roll cube [yes] [no] triangular prism [yes] [no] cylinder [yes] [yes] cone [no] [yes] pyramid [no] [no] sphere [no] [yes] sOLIDS RIDDLES Group Size: Whole Class or Small Groups Procedure: Provide a set of six GeoSolids shapes to be placed on classroom display or provide a set of solids – cube, cylinder, sphere, cone, triangular prism, and pyramid – for each group of students. Hold up each solid and challenge students to name an everyday or classroom object that matches the shape of the solid. n sphere [globe, ball...] n cube [box, carton...] n cylinder [oatmeal box, 35-mm film canister...] n cone [ice cream cone, coffee filter...] n triangular prism [napkin holder, gift box...] n pyramid [tent, pyramid structure...] Challenge your students to name the solids from the following descriptions. 6 n I am a solid that cannot roll. All my sides are the same size. I am the _____. [cube] n I am a solid that can roll. I have no corners and no flat sides. I am the _____. [sphere] n I am a solid that can roll.
Load more

Recommended publications
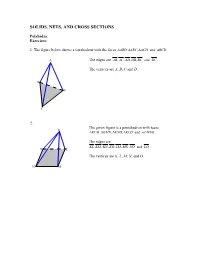
  • Solids, Nets, and Cross Sections
    SOLIDS, NETS, AND CROSS SECTIONS Polyhedra: Exercises: 1. The figure below shows a tetrahedron with the faces ∆ABD,,∆∆ ABC ACD and ∆ BCD . A The edges are AB,,,, AC AD DB BC and DC . The vertices are A, B, C and D, D B C 2. The given figure is a pentahedron with faces K ∆KLM,∆∆∆ KMN , KNO , KLO and . LMNO . The edges are KL,,,,,, KM KN KO LM MN NO and LO . O L The vertices are K, L, M, N, and O. N M Prisms: Exercises (page-4): 1. The right regular octagonal prism has 8 lateral faces, so totally it has 10 faces. It has 24 edges, 8 of them are lateral edges. The prism has 16 vertices. 2. The figure below illustrates an oblique regular triangular prism. It has 5 faces (3 of them are lateral faces), 3 lateral edges and totally 9 edges. The prism has 6 vertices. Pyramids Exercises (page-6): 1. The pentagonal pyramid has 5 lateral faces and thus 6 faces in total. It has 5 lateral edges, 10 edges and 6 vertices. 2. The hexagonal pyramid has 6 lateral faces and 7 faces in total. It has 6 lateral edges, 12 edges and 7 vertices. Nets Exercises: 1. Regular right hexagonal pyramid 2. Rectangular prism 3. Regular right octagonal prism 4. Regular oblique hexagonal prism 5. and so on… 6. Right Cylinder 7. Right Cone Cross sections: Exercises (page-15): 1. i) In the cross section parallel to the base, the cross section is a regular hexagon of the same size as the base.
    [Show full text]
  • 2D and 3D Shapes.Pdf
    & • Anchor 2 - D Charts • Flash Cards 3 - D • Shape Books • Practice Pages rd Shapesfor 3 Grade by Carrie Lutz T hank you for purchasing!!! Check out my store: http://www.teacherspayteachers.com/Store/Carrie-Lutz-6 Follow me for notifications of freebies, sales and new arrivals! Visit my BLOG for more Free Stuff! Read My Blog Post about Teaching 3 Dimensional Figures Correctly Credits: Carrie Lutz©2016 2D Shape Bank 3D Shape Bank 3 Sided 5 Sided Prisms triangular prism cube rectangular prism triangle pentagon 4 Sided rectangle square pentagonal prism hexagonal prism octagonal prism Pyramids rhombus trapezoid 6 Sided 8 Sided rectangular square triangular pyramid pyramid pyramid Carrie LutzCarrie CarrieLutz pentagonal hexagonal © hexagon octagon © 2016 pyramid pyramid 2016 Curved Shapes CURVED SOLIDS oval circle sphere cone cylinder Carrie Lutz©2016 Carrie Lutz©2016 Name _____________________ Side Sort Date _____________________ Cut out the shapes below and glue them in the correct column. More than 4 Less than 4 Exactly 4 Carrie Lutz©2016 Name _____________________ Name the Shapes Date _____________________ 1. Name the Shape. 2. Name the Shape. 3. Name the Shape. ____________________________________ ____________________________________ ____________________________________ 4. Name the Shape. 5. Name the Shape. 6. Name the Shape. ____________________________________ ____________________________________ ____________________________________ 4. Name the Shape. 5. Name the Shape. 6. Name the Shape. ____________________________________ ____________________________________ ____________________________________ octagon circle square rhombus triangle hexagon pentagon rectangle trapezoid Carrie Lutz©2016 Faces, Edges, Vertices Name _____________________ and Date _____________________ 1. Name the Shape. 2. Name the Shape. 3. Name the Shape. ____________________________________ ____________________________________ ____________________________________ _____ faces _____ faces _____ faces _____Edges _____Edges _____Edges _____Vertices _____Vertices _____Vertices 4.
    [Show full text]
  • Three-Dimensional Figures
    Notes Three-Dimensional Figures Polyhedra (the plural of Polyhedron) are three dimensional versions of polygons. They are made up of polygons. They are solid (no holes) and closed. Polyhedra fall into two major classes: Pyramids and Prisms. Note: Prisms and Pyramids are always named “based” on their bases. A Prism with a square base is called a Square Prism; a pyramid with a square base is called a Square Pyramid; a prism with a base that’s an octagon is called an Octagonal Prism; and so on. General Classes of Polyhedra 1) Prism - polyhedron with two opposite faces identical to each other. These opposite faces are called bases. The other faces are called lateral faces. Using the Power Solids, find all of the Prisms. Decide which faces are the bases, and which faces are the lateral faces. Then write the name of each of the prisms that you found: 2) Pyramid - polyhedron with a top "point" (called an apex), where all lateral faces meet. Using the Power Solids, find the two Pyramids. Decide which face is the base, and which faces are the lateral faces. Write the names of those two pyramids below. Other Three Dimensional Figures 1) Cylinder - curved shape analogous to a prism, except with circles for bases. Question: If the two circles are bases, what is the lateral “face”? 2) Cone - curved shape analogous to a pyramid, except with a circle for a base. Question: If the circle is the base, what is the lateral "face"? Note: The bases of cones and cylinders do not have to be circles (they could be ovals, for example), but we will pay attention to only those with circular bases.
    [Show full text]
  • Triangulations and Simplex Tilings of Polyhedra
    Triangulations and Simplex Tilings of Polyhedra by Braxton Carrigan A dissertation submitted to the Graduate Faculty of Auburn University in partial fulfillment of the requirements for the Degree of Doctor of Philosophy Auburn, Alabama August 4, 2012 Keywords: triangulation, tiling, tetrahedralization Copyright 2012 by Braxton Carrigan Approved by Andras Bezdek, Chair, Professor of Mathematics Krystyna Kuperberg, Professor of Mathematics Wlodzimierz Kuperberg, Professor of Mathematics Chris Rodger, Don Logan Endowed Chair of Mathematics Abstract This dissertation summarizes my research in the area of Discrete Geometry. The par- ticular problems of Discrete Geometry discussed in this dissertation are concerned with partitioning three dimensional polyhedra into tetrahedra. The most widely used partition of a polyhedra is triangulation, where a polyhedron is broken into a set of convex polyhedra all with four vertices, called tetrahedra, joined together in a face-to-face manner. If one does not require that the tetrahedra to meet along common faces, then we say that the partition is a tiling. Many of the algorithmic implementations in the field of Computational Geometry are dependent on the results of triangulation. For example computing the volume of a polyhedron is done by adding volumes of tetrahedra of a triangulation. In Chapter 2 we will provide a brief history of triangulation and present a number of known non-triangulable polyhedra. In this dissertation we will particularly address non-triangulable polyhedra. Our research was motivated by a recent paper of J. Rambau [20], who showed that a nonconvex twisted prisms cannot be triangulated. As in algebra when proving a number is not divisible by 2012 one may show it is not divisible by 2, we will revisit Rambau's results and show a new shorter proof that the twisted prism is non-triangulable by proving it is non-tilable.
    [Show full text]
  • Paper Models of Polyhedra
    Paper Models of Polyhedra Gijs Korthals Altes Polyhedra are beautiful 3-D geometrical figures that have fascinated philosophers, mathematicians and artists for millennia Copyrights © 1998-2001 Gijs.Korthals Altes All rights reserved . It's permitted to make copies for non-commercial purposes only email: [email protected] Paper Models of Polyhedra Platonic Solids Dodecahedron Cube and Tetrahedron Octahedron Icosahedron Archimedean Solids Cuboctahedron Icosidodecahedron Truncated Tetrahedron Truncated Octahedron Truncated Cube Truncated Icosahedron (soccer ball) Truncated dodecahedron Rhombicuboctahedron Truncated Cuboctahedron Rhombicosidodecahedron Truncated Icosidodecahedron Snub Cube Snub Dodecahedron Kepler-Poinsot Polyhedra Great Stellated Dodecahedron Small Stellated Dodecahedron Great Icosahedron Great Dodecahedron Other Uniform Polyhedra Tetrahemihexahedron Octahemioctahedron Cubohemioctahedron Small Rhombihexahedron Small Rhombidodecahedron S mall Dodecahemiododecahedron Small Ditrigonal Icosidodecahedron Great Dodecahedron Compounds Stella Octangula Compound of Cube and Octahedron Compound of Dodecahedron and Icosahedron Compound of Two Cubes Compound of Three Cubes Compound of Five Cubes Compound of Five Octahedra Compound of Five Tetrahedra Compound of Truncated Icosahedron and Pentakisdodecahedron Other Polyhedra Pentagonal Hexecontahedron Pentagonalconsitetrahedron Pyramid Pentagonal Pyramid Decahedron Rhombic Dodecahedron Great Rhombihexacron Pentagonal Dipyramid Pentakisdodecahedron Small Triakisoctahedron Small Triambic
    [Show full text]
  • Bearings and Bushings
    BEARINGS AND BUSHINGS. [1457] AT LEAST ONE; Plain bearing. Load bearing. Journal bearing. Track bearing. Bushing and bearing vibration and shock isolators made of rubber, syntactic rubber, polyurethane. Pillow block bearing with at least one bolt. Flange bearing unit with at least one bolt. Ball and roller Thrust bearing. Spherical bearing. Cylindrical bearing. Rodend bearing. Magnetic Jewel bearing. Pair of Magnet load bearing. Air bearing. Fluid bearing. Turbo bearing. eccentric bearing. Spherical roller bearings. Cylindrical roller. Ball bearing. Gear bearing. Tapered roller. Needle roller bearing. Carb toroidal roller bearings. Thrust loads. Radial bearing. Composite bearing. Slewing bearings. Ball bearings. Rollers bearings. Race bearings. Pillow block bearings. Linear track slide or roller bearing. Linear electromagnetic bearing. Linear bushing bearing H/V. Hybrid ball bearings. Linear plain bushing. Self-aligning ball bearings. Linear slide bearing and bushing. Stainless steel raceway. Slides and roller slides bearings. Rack slides. Track roller. Ball screw. Lead screw. Ball spline linear bearing. Temperature bearing. Flexible bearing. Track bearing. bearing seal and bushing. Unidirectional gear bearing. Swash bearing and anchor. Pitch bearing. Hinge bearing. Pivot bearing. One way bearing. One-way Gear. bearing. Anti-reverse bearing. Clutch needle bearing. Integral radial bearings. [1458] Linear bearing and bushing. Double row bearing. EMQ bearings. Stainless steel alloy unit for bearing mount and bearing flange mount. Flexible Oil seal. Oil filled bushing. Cage type bearing. Gasket O, Rings. Ceramic bearings. Tapered roller bearings. High grade thrust washers Chrome, stainless Steel. Instrument bearing flow meter bearing. Plastic bearing. Insert full ceramic bearing. Bearing Mount and suspension unit. Thermoplastic bearings. Plastic bearings. Pressure Roller bearings.
    [Show full text]
  • Geometry in Design Geometrical Construction in 3D Forms by Prof
    D’source 1 Digital Learning Environment for Design - www.dsource.in Design Course Geometry in Design Geometrical Construction in 3D Forms by Prof. Ravi Mokashi Punekar and Prof. Avinash Shide DoD, IIT Guwahati Source: http://www.dsource.in/course/geometry-design 1. Introduction 2. Golden Ratio 3. Polygon - Classification - 2D 4. Concepts - 3 Dimensional 5. Family of 3 Dimensional 6. References 7. Contact Details D’source 2 Digital Learning Environment for Design - www.dsource.in Design Course Introduction Geometry in Design Geometrical Construction in 3D Forms Geometry is a science that deals with the study of inherent properties of form and space through examining and by understanding relationships of lines, surfaces and solids. These relationships are of several kinds and are seen in Prof. Ravi Mokashi Punekar and forms both natural and man-made. The relationships amongst pure geometric forms possess special properties Prof. Avinash Shide or a certain geometric order by virtue of the inherent configuration of elements that results in various forms DoD, IIT Guwahati of symmetry, proportional systems etc. These configurations have properties that hold irrespective of scale or medium used to express them and can also be arranged in a hierarchy from the totally regular to the amorphous where formal characteristics are lost. The objectives of this course are to study these inherent properties of form and space through understanding relationships of lines, surfaces and solids. This course will enable understanding basic geometric relationships, Source: both 2D and 3D, through a process of exploration and analysis. Concepts are supported with 3Dim visualization http://www.dsource.in/course/geometry-design/in- of models to understand the construction of the family of geometric forms and space interrelationships.
    [Show full text]
  • 10.1. CRYSTALLOGRAPHIC and NONCRYSTALLOGRAPHIC POINT GROUPS Table 10.1.1.2
    International Tables for Crystallography (2006). Vol. A, Section 10.1.2, pp. 763–795. 10.1. CRYSTALLOGRAPHIC AND NONCRYSTALLOGRAPHIC POINT GROUPS Table 10.1.1.2. The 32 three-dimensional crystallographic point groups, arranged according to crystal system (cf. Chapter 2.1) Full Hermann–Mauguin (left) and Schoenflies symbols (right). Dashed lines separate point groups with different Laue classes within one crystal system. Crystal system General Monoclinic (top) symbol Triclinic Orthorhombic (bottom) Tetragonal Trigonal Hexagonal Cubic n 1 C1 2 C2 4 C4 3 C3 6 C6 23 T n 1 Ci m 2 Cs 4 S4 3 C3i 6 3=mC3h –– n=m 2=mC2h 4=mC4h ––6=mC6h 2=m3 Th n22 222 D2 422 D4 32 D3 622 D6 432 O nmm mm2 C2v 4mm C4v 3mC3v 6mm C6v –– n2m ––42mD2d 32=mD3d 62mD3h 43mTd n=m 2=m 2=m 2=m 2=m 2=mD2h 4=m 2=m 2=mD4h ––6=m 2=m 2=mD6h 4=m 32=mOh 10.1.2. Crystallographic point groups the a axis points down the page and the b axis runs horizontally from left to right. For the five trigonal point groups, the c axis is 10.1.2.1. Description of point groups normal to the page only for the description with ‘hexagonal axes’; if In crystallography, point groups usually are described described with ‘rhombohedral axes’, the direction [111] is normal (i) by means of their Hermann–Mauguin or Schoenflies symbols; and the positive a axis slopes towards the observer. The (ii) by means of their stereographic projections; conventional coordinate systems used for the various crystal (iii) by means of the matrix representations of their symmetry systems are listed in Table 2.1.2.1 and illustrated in Figs.
    [Show full text]
  • Arxiv:1908.05395V1 [Math.MG] 15 Aug 2019
    Draft version August 16, 2019 Typeset using LATEX default style in AASTeX62 Envelope Polyhedra J. Richard Gott, III1 1Department of Astrophysical Sciences Princeton University Princeton, NJ 08544, USA ABSTRACT This paper presents an additional class of regular polyhedra|envelope polyhedra|made of regular polygons, where the arrangement of polygons (creating a single surface) around each vertex is identical; but dihedral angles between faces need not be identical, and some of the dihedral angles are 0◦ (i.e., some polygons are placed back to back). For example, squares{6 around a point f4,6g is produced by deleting the triangles from the rhombicuboctahedron, creating a hollow polyhedron of genus 7 with triangular holes connecting 18 interior and 18 exterior square faces. An empty cube missing its top and bottom faces becomes an envelope polyhedron, squares{4 around a point f4,4g with a toroidal topology. This definition leads to many interesting finite and infinite multiply connected regular polygon networks, including one infinite network with squares{14 around a point f4,14g and another with triangles{18 around a point f3,18g. These are introduced just over 50 years after my related paper on infinite spongelike pseudopolyhedra in American Mathematical Monthly (Gott, 1967). Keywords: geometry, polyhedra 1. INTRODUCTION|PSEUDOPOLYHEDRA My work on envelope polyhedra grows directly out of my earlier work on pseudopolyhedra, which I will describe first. This was my high school science fair project which won 1st Place in mathematics at the (May, 1965) National Science Fair International (now the Intel International Science and Engineering Fair). A picture of this project appears in my book The Cosmic Web (2016), along with a description.
    [Show full text]
  • Do What You Can. These Activities Are for the Week. If You Feel Like Y
    Week beginning 18/05/2020 Maths Week 5 Remember – Do what you can. These activities are for the week. If you feel like you are up for the extra challenge, BBC Bitesize have new daily lessons for English and Maths on their website. These are specific for each year group. You also have the online White Rose Maths that have daily Maths lessons and the new Maths Shed resource. Both of these are excellent resources and you will be able to extend this work on shape through them. The following is learning you would have been doing at school with us. Starters – try doing one every day: These starters are objectives that you have learnt in Year 5. • Revise times tables and all related division facts. • Pick a number between 0 and 20 or 20 and 100. Now double that number. Now try halving that number. Use partitioning to help you. Repeat with 10 other numbers. • Write equivalent fractions and decimals for: 25%, 50%, 75%, 33%, 89%, 90%, 2%, 8% and 16%. • Find ½, ¼ and 1/10 of: 20, 36, 40, 60, 66 and 72. • Multiply these numbers by 10,100 and 1000: 6, 17, 26, 59, 66 and 101. Can you remember the rules? Write them down. You can use the squares below to move the digits if you need to. Shape Week 2 L.O. To identify the properties of prisms and pyramids. Knowledge: A pyramid is named after the shape of the base as you can see from the above. The number of triangular faces the shape has, depends upon how many edges the polygon shape at the bottom has.
    [Show full text]
  • Shaping Space Exploring Polyhedra in Nature, Art, and the Geometrical Imagination
    Shaping Space Exploring Polyhedra in Nature, Art, and the Geometrical Imagination Marjorie Senechal Editor Shaping Space Exploring Polyhedra in Nature, Art, and the Geometrical Imagination with George Fleck and Stan Sherer 123 Editor Marjorie Senechal Department of Mathematics and Statistics Smith College Northampton, MA, USA ISBN 978-0-387-92713-8 ISBN 978-0-387-92714-5 (eBook) DOI 10.1007/978-0-387-92714-5 Springer New York Heidelberg Dordrecht London Library of Congress Control Number: 2013932331 Mathematics Subject Classification: 51-01, 51-02, 51A25, 51M20, 00A06, 00A69, 01-01 © Marjorie Senechal 2013 This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, reuse of illustrations, recitation, broadcasting, reproduction on microfilms or in any other physical way, and transmission or information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed. Exempted from this legal reservation are brief excerpts in connection with reviews or scholarly analysis or material supplied specifically for the purpose of being entered and executed on a computer system, for exclusive use by the purchaser of the work. Duplication of this publication or parts thereof is permitted only under the provisions of the Copyright Law of the Publishers location, in its current version, and permission for use must always be obtained from Springer. Permissions for use may be obtained through RightsLink at the Copyright Clearance Center. Violations are liable to prosecution under the respective Copyright Law. The use of general descriptive names, registered names, trademarks, service marks, etc.
    [Show full text]
  • Reteach 10-1 Introduction to Three-Dimensional Figures a Polyhedron Is a Three-Dimensional Figure Whose Faces Are Polygons
    MSM07G7_RESBK_CH10_003–010.pe 2/14/06 11:27 AM Page 6 Name Date Class LESSON Reteach 10-1 Introduction to Three-Dimensional Figures A polyhedron is a three-dimensional figure whose faces are polygons. There are two types of polyhedrons. Prisms Pyramids A prism has 2 bases that are congruent A pyramid has one base that is a and parallel polygons. The other faces polygon. Its faces are triangles that are parallelograms or rectangles. meet at one vertex. Prisms and pyramids are named by their bases. 1. Look at the figure at the right. Its base is a square . Its faces are triane, . It is called a square pyramid. 2. Look at the figure at the right. It has 2 congruent and parallel bases that are triane, . Its faces are triane, . It is called a pentagonal prism. If a three-dimensional figure has a face that is curved, it is not a polyhedron. not a polyhedron Is each figure a polyhedron? 3. 4. 5. triane, no triane, Copyright © by Holt, Rinehart and Winston. All rights reserved. 6 Holt Mathematics MSM07G7_RESBK_Ch10_045-055.pe 2/14/06 11:50 AM Page 45 LESSON Practice A LESSON Practice B 10-1 Introduction to Three-Dimensional Figures 10-1 Introduction to Three-Dimensional Figures Identify the base of each prism or pyramid. Then choose the Identify the base or bases of each figure. Then name the figure. name of the prism or pyramid from the box. 1. 2. 3. rectangular prism square pyramid triangular prism pentagonal prism square prism triangular pyramid hexagonal prism rectangular pyramid hexagonal pyramid pentagonal pyramid octagonal prism 1.
    [Show full text]