DOCSLIB.ORG

Geometry Worksheet -- Classifying Prisms

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Geometry Worksheet -- Classifying Prisms Classifying Prisms (A) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (A) Answers Name each prism based on the shape of its base. hexagonal prism triangular prism pentagonal prism rectangular prism square prism pentagonal prism square prism, cube heptagonal prism Math-Drills.com Classifying Prisms (B) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (B) Answers Name each prism based on the shape of its base. hexagonal prism octagonal prism heptagonal prism rectangular prism square prism, cube hexagonal prism triangular prism square prism Math-Drills.com Classifying Prisms (C) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (C) Answers Name each prism based on the shape of its base. octagonal prism square prism rectangular prism square prism triangular prism square prism, cube heptagonal prism hexagonal prism Math-Drills.com Classifying Prisms (D) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (D) Answers Name each prism based on the shape of its base. hexagonal prism square prism octagonal prism pentagonal prism rectangular prism square prism, cube hexagonal prism triangular prism Math-Drills.com Classifying Prisms (E) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (E) Answers Name each prism based on the shape of its base. pentagonal prism square prism, cube square prism heptagonal prism rectangular prism pentagonal prism triangular prism octagonal prism Math-Drills.com Classifying Prisms (F) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (F) Answers Name each prism based on the shape of its base. triangular prism rectangular prism heptagonal prism hexagonal prism square prism, cube octagonal prism rectangular prism square prism Math-Drills.com Classifying Prisms (G) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (G) Answers Name each prism based on the shape of its base. square prism, cube rectangular prism triangular prism heptagonal prism hexagonal prism square prism square prism, cube octagonal prism Math-Drills.com Classifying Prisms (H) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (H) Answers Name each prism based on the shape of its base. octagonal prism heptagonal prism square prism pentagonal prism heptagonal prism triangular prism rectangular prism square prism, cube Math-Drills.com Classifying Prisms (I) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (I) Answers Name each prism based on the shape of its base. square prism, cube hexagonal prism pentagonal prism octagonal prism square prism, cube triangular prism square prism rectangular prism Math-Drills.com Classifying Prisms (J) Name each prism based on the shape of its base. Math-Drills.com Classifying Prisms (J) Answers Name each prism based on the shape of its base. square prism rectangular prism triangular prism square prism, cube rectangular prism octagonal prism hexagonal prism pentagonal prism Math-Drills.com.
Load more

Recommended publications
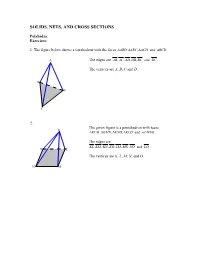
  • Solids, Nets, and Cross Sections
    SOLIDS, NETS, AND CROSS SECTIONS Polyhedra: Exercises: 1. The figure below shows a tetrahedron with the faces ∆ABD,,∆∆ ABC ACD and ∆ BCD . A The edges are AB,,,, AC AD DB BC and DC . The vertices are A, B, C and D, D B C 2. The given figure is a pentahedron with faces K ∆KLM,∆∆∆ KMN , KNO , KLO and . LMNO . The edges are KL,,,,,, KM KN KO LM MN NO and LO . O L The vertices are K, L, M, N, and O. N M Prisms: Exercises (page-4): 1. The right regular octagonal prism has 8 lateral faces, so totally it has 10 faces. It has 24 edges, 8 of them are lateral edges. The prism has 16 vertices. 2. The figure below illustrates an oblique regular triangular prism. It has 5 faces (3 of them are lateral faces), 3 lateral edges and totally 9 edges. The prism has 6 vertices. Pyramids Exercises (page-6): 1. The pentagonal pyramid has 5 lateral faces and thus 6 faces in total. It has 5 lateral edges, 10 edges and 6 vertices. 2. The hexagonal pyramid has 6 lateral faces and 7 faces in total. It has 6 lateral edges, 12 edges and 7 vertices. Nets Exercises: 1. Regular right hexagonal pyramid 2. Rectangular prism 3. Regular right octagonal prism 4. Regular oblique hexagonal prism 5. and so on… 6. Right Cylinder 7. Right Cone Cross sections: Exercises (page-15): 1. i) In the cross section parallel to the base, the cross section is a regular hexagon of the same size as the base.
    [Show full text]
  • Year 6 – Wednesday 24Th June 2020 – Maths
    1 Year 6 – Wednesday 24th June 2020 – Maths Can I identify 3D shapes that have pairs of parallel or perpendicular edges? Parallel – edges that have the same distance continuously between them – parallel edges never meet. Perpendicular – when two edges or faces meet and create a 90o angle. 1 4. 7. 10. 2 5. 8. 11. 3. 6. 9. 12. C1 – Using the shapes above: 1. Name and sort the shapes into: a. Pyramids b. Prisms 2. Draw a table to identify how many faces, edges and vertices each shape has. 3. Write your own geometric definition: a. Prism b. pyramid 4. Which shape is the odd one out? Explain why. C2 – Using the shapes above; 1. Which of the shapes have pairs of parallel edges in: a. All their faces? b. More than one half of the faces? c. One face only? 2. The following shapes have pairs of perpendicular edges. Identify the faces they are in: 2 a. A cube b. A square based pyramid c. A triangular prism d. A cuboid 3. Which shape with straight edges has no perpendicular edges? 4. Which shape has perpendicular edges in the shape but not in any face? C3 – Using the above shapes: 1. How many faces have pairs of parallel edges in: a. A hexagonal pyramid? b. A decagonal (10-sided) based prism? c. A heptagonal based prism? d. Which shape has no face with parallel edges but has parallel edges in the shape? 2. How many faces have perpendicular edges in: a. A pentagonal pyramid b. A hexagonal pyramid c.
    [Show full text]
  • Unit 6 Visualising Solid Shapes(Final)
    • 3D shapes/objects are those which do not lie completely in a plane. • 3D objects have different views from different positions. • A solid is a polyhedron if it is made up of only polygonal faces, the faces meet at edges which are line segments and the edges meet at a point called vertex. • Euler’s formula for any polyhedron is, F + V – E = 2 Where F stands for number of faces, V for number of vertices and E for number of edges. • Types of polyhedrons: (a) Convex polyhedron A convex polyhedron is one in which all faces make it convex. e.g. (1) (2) (3) (4) 12/04/18 (1) and (2) are convex polyhedrons whereas (3) and (4) are non convex polyhedron. (b) Regular polyhedra or platonic solids: A polyhedron is regular if its faces are congruent regular polygons and the same number of faces meet at each vertex. For example, a cube is a platonic solid because all six of its faces are congruent squares. There are five such solids– tetrahedron, cube, octahedron, dodecahedron and icosahedron. e.g. • A prism is a polyhedron whose bottom and top faces (known as bases) are congruent polygons and faces known as lateral faces are parallelograms (when the side faces are rectangles, the shape is known as right prism). • A pyramid is a polyhedron whose base is a polygon and lateral faces are triangles. • A map depicts the location of a particular object/place in relation to other objects/places. The front, top and side of a figure are shown. Use centimetre cubes to build the figure.
    [Show full text]
  • Uniform Panoploid Tetracombs
    Uniform Panoploid Tetracombs George Olshevsky TETRACOMB is a four-dimensional tessellation. In any tessellation, the honeycells, which are the n-dimensional polytopes that tessellate the space, Amust by definition adjoin precisely along their facets, that is, their ( n!1)- dimensional elements, so that each facet belongs to exactly two honeycells. In the case of tetracombs, the honeycells are four-dimensional polytopes, or polychora, and their facets are polyhedra. For a tessellation to be uniform, the honeycells must all be uniform polytopes, and the vertices must be transitive on the symmetry group of the tessellation. Loosely speaking, therefore, the vertices must be “surrounded all alike” by the honeycells that meet there. If a tessellation is such that every point of its space not on a boundary between honeycells lies in the interior of exactly one honeycell, then it is panoploid. If one or more points of the space not on a boundary between honeycells lie inside more than one honeycell, the tessellation is polyploid. Tessellations may also be constructed that have “holes,” that is, regions that lie inside none of the honeycells; such tessellations are called holeycombs. It is possible for a polyploid tessellation to also be a holeycomb, but not for a panoploid tessellation, which must fill the entire space exactly once. Polyploid tessellations are also called starcombs or star-tessellations. Holeycombs usually arise when (n!1)-dimensional tessellations are themselves permitted to be honeycells; these take up the otherwise free facets that bound the “holes,” so that all the facets continue to belong to two honeycells. In this essay, as per its title, we are concerned with just the uniform panoploid tetracombs.
    [Show full text]
  • 2D and 3D Shapes.Pdf
    & • Anchor 2 - D Charts • Flash Cards 3 - D • Shape Books • Practice Pages rd Shapesfor 3 Grade by Carrie Lutz T hank you for purchasing!!! Check out my store: http://www.teacherspayteachers.com/Store/Carrie-Lutz-6 Follow me for notifications of freebies, sales and new arrivals! Visit my BLOG for more Free Stuff! Read My Blog Post about Teaching 3 Dimensional Figures Correctly Credits: Carrie Lutz©2016 2D Shape Bank 3D Shape Bank 3 Sided 5 Sided Prisms triangular prism cube rectangular prism triangle pentagon 4 Sided rectangle square pentagonal prism hexagonal prism octagonal prism Pyramids rhombus trapezoid 6 Sided 8 Sided rectangular square triangular pyramid pyramid pyramid Carrie LutzCarrie CarrieLutz pentagonal hexagonal © hexagon octagon © 2016 pyramid pyramid 2016 Curved Shapes CURVED SOLIDS oval circle sphere cone cylinder Carrie Lutz©2016 Carrie Lutz©2016 Name _____________________ Side Sort Date _____________________ Cut out the shapes below and glue them in the correct column. More than 4 Less than 4 Exactly 4 Carrie Lutz©2016 Name _____________________ Name the Shapes Date _____________________ 1. Name the Shape. 2. Name the Shape. 3. Name the Shape. ____________________________________ ____________________________________ ____________________________________ 4. Name the Shape. 5. Name the Shape. 6. Name the Shape. ____________________________________ ____________________________________ ____________________________________ 4. Name the Shape. 5. Name the Shape. 6. Name the Shape. ____________________________________ ____________________________________ ____________________________________ octagon circle square rhombus triangle hexagon pentagon rectangle trapezoid Carrie Lutz©2016 Faces, Edges, Vertices Name _____________________ and Date _____________________ 1. Name the Shape. 2. Name the Shape. 3. Name the Shape. ____________________________________ ____________________________________ ____________________________________ _____ faces _____ faces _____ faces _____Edges _____Edges _____Edges _____Vertices _____Vertices _____Vertices 4.
    [Show full text]
  • Lesson 23: the Volume of a Right Prism
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 23 7•3 Lesson 23: The Volume of a Right Prism Student Outcomes . Students use the known formula for the volume of a right rectangular prism (length × width × height). Students understand the volume of a right prism to be the area of the base times the height. Students compute volumes of right prisms involving fractional values for length. Lesson Notes Students extend their knowledge of obtaining volumes of right rectangular prisms via dimensional measurements to understand how to calculate the volumes of other right prisms. This concept will later be extended to finding the volumes of liquids in right prism-shaped containers and extended again (in Module 6) to finding the volumes of irregular solids using displacement of liquids in containers. The Problem Set scaffolds in the use of equations to calculate unknown dimensions. Classwork Opening Exercise (5 minutes) Opening Exercise The volume of a solid is a quantity given by the number of unit cubes needed to fill the solid. Most solids—rocks, baseballs, people—cannot be filled with unit cubes or assembled from cubes. Yet such solids still have volume. Fortunately, we do not need to assemble solids from unit cubes in order to calculate their volume. One of the first interesting examples of a solid that cannot be assembled from cubes, but whose volume can still be calculated from a formula, is a right triangular prism. What is the area of the square pictured on the right? Explain. The area of the square is ퟑퟔ 퐮퐧퐢퐭퐬ퟐ because the region is filled with ퟑퟔ square regions that are ퟏ 퐮퐧퐢퐭 by ퟏ 퐮퐧퐢퐭, or ퟏ 퐮퐧퐢퐭ퟐ.
    [Show full text]
  • Three-Dimensional Figures
    Notes Three-Dimensional Figures Polyhedra (the plural of Polyhedron) are three dimensional versions of polygons. They are made up of polygons. They are solid (no holes) and closed. Polyhedra fall into two major classes: Pyramids and Prisms. Note: Prisms and Pyramids are always named “based” on their bases. A Prism with a square base is called a Square Prism; a pyramid with a square base is called a Square Pyramid; a prism with a base that’s an octagon is called an Octagonal Prism; and so on. General Classes of Polyhedra 1) Prism - polyhedron with two opposite faces identical to each other. These opposite faces are called bases. The other faces are called lateral faces. Using the Power Solids, find all of the Prisms. Decide which faces are the bases, and which faces are the lateral faces. Then write the name of each of the prisms that you found: 2) Pyramid - polyhedron with a top "point" (called an apex), where all lateral faces meet. Using the Power Solids, find the two Pyramids. Decide which face is the base, and which faces are the lateral faces. Write the names of those two pyramids below. Other Three Dimensional Figures 1) Cylinder - curved shape analogous to a prism, except with circles for bases. Question: If the two circles are bases, what is the lateral “face”? 2) Cone - curved shape analogous to a pyramid, except with a circle for a base. Question: If the circle is the base, what is the lateral "face"? Note: The bases of cones and cylinders do not have to be circles (they could be ovals, for example), but we will pay attention to only those with circular bases.
    [Show full text]
  • [ENTRY POLYHEDRA] Authors: Oliver Knill: December 2000 Source: Translated Into This Format from Data Given In
    ENTRY POLYHEDRA [ENTRY POLYHEDRA] Authors: Oliver Knill: December 2000 Source: Translated into this format from data given in http://netlib.bell-labs.com/netlib tetrahedron The [tetrahedron] is a polyhedron with 4 vertices and 4 faces. The dual polyhedron is called tetrahedron. cube The [cube] is a polyhedron with 8 vertices and 6 faces. The dual polyhedron is called octahedron. hexahedron The [hexahedron] is a polyhedron with 8 vertices and 6 faces. The dual polyhedron is called octahedron. octahedron The [octahedron] is a polyhedron with 6 vertices and 8 faces. The dual polyhedron is called cube. dodecahedron The [dodecahedron] is a polyhedron with 20 vertices and 12 faces. The dual polyhedron is called icosahedron. icosahedron The [icosahedron] is a polyhedron with 12 vertices and 20 faces. The dual polyhedron is called dodecahedron. small stellated dodecahedron The [small stellated dodecahedron] is a polyhedron with 12 vertices and 12 faces. The dual polyhedron is called great dodecahedron. great dodecahedron The [great dodecahedron] is a polyhedron with 12 vertices and 12 faces. The dual polyhedron is called small stellated dodecahedron. great stellated dodecahedron The [great stellated dodecahedron] is a polyhedron with 20 vertices and 12 faces. The dual polyhedron is called great icosahedron. great icosahedron The [great icosahedron] is a polyhedron with 12 vertices and 20 faces. The dual polyhedron is called great stellated dodecahedron. truncated tetrahedron The [truncated tetrahedron] is a polyhedron with 12 vertices and 8 faces. The dual polyhedron is called triakis tetrahedron. cuboctahedron The [cuboctahedron] is a polyhedron with 12 vertices and 14 faces. The dual polyhedron is called rhombic dodecahedron.
    [Show full text]
  • Triangulations and Simplex Tilings of Polyhedra
    Triangulations and Simplex Tilings of Polyhedra by Braxton Carrigan A dissertation submitted to the Graduate Faculty of Auburn University in partial fulfillment of the requirements for the Degree of Doctor of Philosophy Auburn, Alabama August 4, 2012 Keywords: triangulation, tiling, tetrahedralization Copyright 2012 by Braxton Carrigan Approved by Andras Bezdek, Chair, Professor of Mathematics Krystyna Kuperberg, Professor of Mathematics Wlodzimierz Kuperberg, Professor of Mathematics Chris Rodger, Don Logan Endowed Chair of Mathematics Abstract This dissertation summarizes my research in the area of Discrete Geometry. The par- ticular problems of Discrete Geometry discussed in this dissertation are concerned with partitioning three dimensional polyhedra into tetrahedra. The most widely used partition of a polyhedra is triangulation, where a polyhedron is broken into a set of convex polyhedra all with four vertices, called tetrahedra, joined together in a face-to-face manner. If one does not require that the tetrahedra to meet along common faces, then we say that the partition is a tiling. Many of the algorithmic implementations in the field of Computational Geometry are dependent on the results of triangulation. For example computing the volume of a polyhedron is done by adding volumes of tetrahedra of a triangulation. In Chapter 2 we will provide a brief history of triangulation and present a number of known non-triangulable polyhedra. In this dissertation we will particularly address non-triangulable polyhedra. Our research was motivated by a recent paper of J. Rambau [20], who showed that a nonconvex twisted prisms cannot be triangulated. As in algebra when proving a number is not divisible by 2012 one may show it is not divisible by 2, we will revisit Rambau's results and show a new shorter proof that the twisted prism is non-triangulable by proving it is non-tilable.
    [Show full text]
  • Paper Models of Polyhedra
    Paper Models of Polyhedra Gijs Korthals Altes Polyhedra are beautiful 3-D geometrical figures that have fascinated philosophers, mathematicians and artists for millennia Copyrights © 1998-2001 Gijs.Korthals Altes All rights reserved . It's permitted to make copies for non-commercial purposes only email: [email protected] Paper Models of Polyhedra Platonic Solids Dodecahedron Cube and Tetrahedron Octahedron Icosahedron Archimedean Solids Cuboctahedron Icosidodecahedron Truncated Tetrahedron Truncated Octahedron Truncated Cube Truncated Icosahedron (soccer ball) Truncated dodecahedron Rhombicuboctahedron Truncated Cuboctahedron Rhombicosidodecahedron Truncated Icosidodecahedron Snub Cube Snub Dodecahedron Kepler-Poinsot Polyhedra Great Stellated Dodecahedron Small Stellated Dodecahedron Great Icosahedron Great Dodecahedron Other Uniform Polyhedra Tetrahemihexahedron Octahemioctahedron Cubohemioctahedron Small Rhombihexahedron Small Rhombidodecahedron S mall Dodecahemiododecahedron Small Ditrigonal Icosidodecahedron Great Dodecahedron Compounds Stella Octangula Compound of Cube and Octahedron Compound of Dodecahedron and Icosahedron Compound of Two Cubes Compound of Three Cubes Compound of Five Cubes Compound of Five Octahedra Compound of Five Tetrahedra Compound of Truncated Icosahedron and Pentakisdodecahedron Other Polyhedra Pentagonal Hexecontahedron Pentagonalconsitetrahedron Pyramid Pentagonal Pyramid Decahedron Rhombic Dodecahedron Great Rhombihexacron Pentagonal Dipyramid Pentakisdodecahedron Small Triakisoctahedron Small Triambic
    [Show full text]
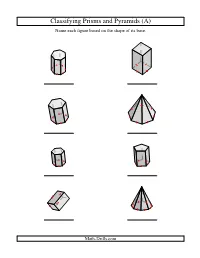
  • Geometry Worksheet -- Classifying Prisms and Pyramids
    Classifying Prisms and Pyramids (A) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (A) Answers Name each figure based on the shape of its base. heptagonal prism square prism hexagonal prism heptagonal pyramid hexagonal prism pentagonal prism rectangular prism octagonal pyramid Math-Drills.com Classifying Prisms and Pyramids (B) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (B) Answers Name each figure based on the shape of its base. square prism heptagonal pyramid pentagonal pyramid triangular prism square pyramid rectangular prism triangular prism rectangular pyramid Math-Drills.com Classifying Prisms and Pyramids (C) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (C) Answers Name each figure based on the shape of its base. pentagonal pyramid square prism, cube octagonal prism heptagonal pyramid heptagonal pyramid rectangular pyramid rectangular prism pentagonal prism Math-Drills.com Classifying Prisms and Pyramids (D) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (D) Answers Name each figure based on the shape of its base. square pyramid heptagonal prism hexagonal prism heptagonal pyramid square prism, cube square pyramid triangular prism octagonal prism Math-Drills.com Classifying Prisms and Pyramids (E) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (E) Answers Name each figure based on the shape of its base. square prism octagonal prism rectangular prism octagonal prism pentagonal pyramid hexagonal prism pentagonal prism heptagonal pyramid Math-Drills.com Classifying Prisms and Pyramids (F) Name each figure based on the shape of its base.
    [Show full text]
  • Bearings and Bushings
    BEARINGS AND BUSHINGS. [1457] AT LEAST ONE; Plain bearing. Load bearing. Journal bearing. Track bearing. Bushing and bearing vibration and shock isolators made of rubber, syntactic rubber, polyurethane. Pillow block bearing with at least one bolt. Flange bearing unit with at least one bolt. Ball and roller Thrust bearing. Spherical bearing. Cylindrical bearing. Rodend bearing. Magnetic Jewel bearing. Pair of Magnet load bearing. Air bearing. Fluid bearing. Turbo bearing. eccentric bearing. Spherical roller bearings. Cylindrical roller. Ball bearing. Gear bearing. Tapered roller. Needle roller bearing. Carb toroidal roller bearings. Thrust loads. Radial bearing. Composite bearing. Slewing bearings. Ball bearings. Rollers bearings. Race bearings. Pillow block bearings. Linear track slide or roller bearing. Linear electromagnetic bearing. Linear bushing bearing H/V. Hybrid ball bearings. Linear plain bushing. Self-aligning ball bearings. Linear slide bearing and bushing. Stainless steel raceway. Slides and roller slides bearings. Rack slides. Track roller. Ball screw. Lead screw. Ball spline linear bearing. Temperature bearing. Flexible bearing. Track bearing. bearing seal and bushing. Unidirectional gear bearing. Swash bearing and anchor. Pitch bearing. Hinge bearing. Pivot bearing. One way bearing. One-way Gear. bearing. Anti-reverse bearing. Clutch needle bearing. Integral radial bearings. [1458] Linear bearing and bushing. Double row bearing. EMQ bearings. Stainless steel alloy unit for bearing mount and bearing flange mount. Flexible Oil seal. Oil filled bushing. Cage type bearing. Gasket O, Rings. Ceramic bearings. Tapered roller bearings. High grade thrust washers Chrome, stainless Steel. Instrument bearing flow meter bearing. Plastic bearing. Insert full ceramic bearing. Bearing Mount and suspension unit. Thermoplastic bearings. Plastic bearings. Pressure Roller bearings.
    [Show full text]