DOCSLIB.ORG

2D and 3D Shapes.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
2D and 3D Shapes.Pdf & • Anchor 2 - D Charts • Flash Cards 3 - D • Shape Books • Practice Pages rd Shapesfor 3 Grade by Carrie Lutz T hank you for purchasing!!! Check out my store: http://www.teacherspayteachers.com/Store/Carrie-Lutz-6 Follow me for notifications of freebies, sales and new arrivals! Visit my BLOG for more Free Stuff! Read My Blog Post about Teaching 3 Dimensional Figures Correctly Credits: Carrie Lutz©2016 2D Shape Bank 3D Shape Bank 3 Sided 5 Sided Prisms triangular prism cube rectangular prism triangle pentagon 4 Sided rectangle square pentagonal prism hexagonal prism octagonal prism Pyramids rhombus trapezoid 6 Sided 8 Sided rectangular square triangular pyramid pyramid pyramid Carrie LutzCarrie CarrieLutz pentagonal hexagonal © hexagon octagon © 2016 pyramid pyramid 2016 Curved Shapes CURVED SOLIDS oval circle sphere cone cylinder Carrie Lutz©2016 Carrie Lutz©2016 Name _____________________ Side Sort Date _____________________ Cut out the shapes below and glue them in the correct column. More than 4 Less than 4 Exactly 4 Carrie Lutz©2016 Name _____________________ Name the Shapes Date _____________________ 1. Name the Shape. 2. Name the Shape. 3. Name the Shape. ____________________________________ ____________________________________ ____________________________________ 4. Name the Shape. 5. Name the Shape. 6. Name the Shape. ____________________________________ ____________________________________ ____________________________________ 4. Name the Shape. 5. Name the Shape. 6. Name the Shape. ____________________________________ ____________________________________ ____________________________________ octagon circle square rhombus triangle hexagon pentagon rectangle trapezoid Carrie Lutz©2016 Faces, Edges, Vertices Name _____________________ and Date _____________________ 1. Name the Shape. 2. Name the Shape. 3. Name the Shape. ____________________________________ ____________________________________ ____________________________________ _____ faces _____ faces _____ faces _____Edges _____Edges _____Edges _____Vertices _____Vertices _____Vertices 4. Name the Shape. 5. Name the Shape. 6. Name the Shape. ____________________________________ ____________________________________ ____________________________________ _____ faces _____ faces _____ faces _____Edges _____Edges _____Edges _____Vertices _____Vertices _____Vertices rectangular prism hexagonal prism pentagonal pyramid triangular prism square pyramid cube Carrie Lutz©2016 Faces, Edges, Vertices Name _____________________ and Date _____________________ 1. What is the difference in 2. What is the difference in 3. What is the difference in the number of faces on the number of vertices on the number of edges on these solid figures? these solid figures? these solid figures? A. 3 A. 1 A. 5 B. 1 B. 2 B. 3 C. 0 C. 4 C. 6 D. 4 D. 3 D. 4 4. What is the difference in 5. What is the difference in 6. What is the difference in the number of vertices on the number of faces on the number of faces on these solid figures? these solid figures? these solid figures? A. 2 A. 5 A. 4 B. 6 B. 4 B. 3 C. 1 C. 2 C. 0 D. 3 D. 8 D. 2 Carrie Lutz©2016.
Load more

Recommended publications
  • Build a Tetrahedral Kite
    Aeronautics Research Mission Directorate Build a Tetrahedral Kite Suggested Grades: 8-12 Activity Overview Time: 90-120 minutes In this activity, you will build a tetrahedral kite from Materials household supplies. • 24 straws (8 inches or less) - NOTE: The straws need to be Steps straight and the same length. If only flexible straws are available, 1. Cut a length of yarn/string 4 feet long. then cut off the flexible portion. • Two or three large spools of 2. Take six straws and place them on a flat surface. cotton string or yarn (approximately 100 feet total) 3. Use your piece of string to join three straws • Scissors together in a triangular shape. On the side where • Hot glue gun and hot glue sticks the two strings are extending from it, one end • Ruler or dowel rod for kite bridle should be approximately 20 inches long, and the • Four pieces of tissue paper (24 x other should be approximately 4 inches long. 18 inches or larger) See Figure 1. • All-purpose glue stick Figure 1 4. Tie these two ends of the string tightly together. Make sure there is no room for the triangle to wiggle. 5. The three straws should form a tight triangle. 6. Cut another 4-inch piece of string. 7. Take one end of the 4-inch string, and tie that end to a corner of the triangle that does not have the string ends extending from it. Figure 2. 8. Add two more straws onto the longest piece of string. 9. Next, take the string that holds the two additional straws and tie it to the end of one of the 4-inch strings to make another tight triangle.
    [Show full text]
  • THE GEOMETRY of PYRAMIDS One of the More Interesting Solid
    THE GEOMETRY OF PYRAMIDS One of the more interesting solid structures which has fascinated individuals for thousands of years going all the way back to the ancient Egyptians is the pyramid. It is a structure in which one takes a closed curve in the x-y plane and connects straight lines between every point on this curve and a fixed point P above the centroid of the curve. Classical pyramids such as the structures at Giza have square bases and lateral sides close in form to equilateral triangles. When the closed curve becomes a circle one obtains a cone and this cone becomes a cylindrical rod when point P is moved to infinity. It is our purpose here to discuss the properties of all N sided pyramids including their volume and surface area using only elementary calculus and geometry. Our starting point will be the following sketch- The base represents a regular N sided polygon with side length ‘a’ . The angle between neighboring radial lines r (shown in red) connecting the polygon vertices with its centroid is θ=2π/N. From this it follows, by the law of cosines, that the length r=a/sqrt[2(1- cos(θ))] . The area of the iscosolis triangle of sides r-a-r is- a a 2 a 2 1 cos( ) A r 2 T 2 4 4 (1 cos( ) From this we have that the area of the N sided polygon and hence the pyramid base will be- 2 2 1 cos( ) Na A N base 2 4 1 cos( ) N 2 It readily follows from this result that a square base N=4 has area Abase=a and a hexagon 2 base N=6 yields Abase= 3sqrt(3)a /2.
    [Show full text]
  • Name Date Period 1
    NAME DATE PERIOD Unit 1, Lesson 13: Polyhedra Let’s investigate polyhedra. 13.1: What are Polyhedra? Here are pictures that represent polyhedra: Here are pictures that do not represent polyhedra: 1. Your teacher will give you some figures or objects. Sort them into polyhedra and non- polyhedra. 2. What features helped you distinguish the polyhedra from the other figures? 13.2: Prisms and Pyramids 1. Here are some polyhedra called prisms. 1 NAME DATE PERIOD Here are some polyhedra called pyramids. a. Look at the prisms. What are their characteristics or features? b. Look at the pyramids. What are their characteristics or features? 2 NAME DATE PERIOD 2. Which of the following nets can be folded into Pyramid P? Select all that apply. 3. Your teacher will give your group a set of polygons and assign a polyhedron. a. Decide which polygons are needed to compose your assigned polyhedron. List the polygons and how many of each are needed. b. Arrange the cut-outs into a net that, if taped and folded, can be assembled into the polyhedron. Sketch the net. If possible, find more than one way to arrange the polygons (show a different net for the same polyhedron). Are you ready for more? What is the smallest number of faces a polyhedron can possibly have? Explain how you know. 13.3: Assembling Polyhedra 1. Your teacher will give you the net of a polyhedron. Cut out the net, and fold it along the edges to assemble a polyhedron. Tape or glue the flaps so that there are no unjoined edges.
    [Show full text]
  • Systematics of Atomic Orbital Hybridization of Coordination Polyhedra: Role of F Orbitals
    molecules Article Systematics of Atomic Orbital Hybridization of Coordination Polyhedra: Role of f Orbitals R. Bruce King Department of Chemistry, University of Georgia, Athens, GA 30602, USA; [email protected] Academic Editor: Vito Lippolis Received: 4 June 2020; Accepted: 29 June 2020; Published: 8 July 2020 Abstract: The combination of atomic orbitals to form hybrid orbitals of special symmetries can be related to the individual orbital polynomials. Using this approach, 8-orbital cubic hybridization can be shown to be sp3d3f requiring an f orbital, and 12-orbital hexagonal prismatic hybridization can be shown to be sp3d5f2g requiring a g orbital. The twists to convert a cube to a square antiprism and a hexagonal prism to a hexagonal antiprism eliminate the need for the highest nodality orbitals in the resulting hybrids. A trigonal twist of an Oh octahedron into a D3h trigonal prism can involve a gradual change of the pair of d orbitals in the corresponding sp3d2 hybrids. A similar trigonal twist of an Oh cuboctahedron into a D3h anticuboctahedron can likewise involve a gradual change in the three f orbitals in the corresponding sp3d5f3 hybrids. Keywords: coordination polyhedra; hybridization; atomic orbitals; f-block elements 1. Introduction In a series of papers in the 1990s, the author focused on the most favorable coordination polyhedra for sp3dn hybrids, such as those found in transition metal complexes. Such studies included an investigation of distortions from ideal symmetries in relatively symmetrical systems with molecular orbital degeneracies [1] In the ensuing quarter century, interest in actinide chemistry has generated an increasing interest in the involvement of f orbitals in coordination chemistry [2–7].
    [Show full text]
  • Math 366 Lecture Notes Section 11.4 – Geometry in Three Dimensions
    Section 11-4 Math 366 Lecture Notes Section 11.4 – Geometry in Three Dimensions Simple Closed Surfaces A simple closed surface has exactly one interior, no holes, and is hollow. A sphere is the set of all points at a given distance from a given point, the center . A sphere is a simple closed surface. A solid is a simple closed surface with all interior points. (see p. 726) A polyhedron is a simple closed surface made up of polygonal regions, or faces . The vertices of the polygonal regions are the vertices of the polyhedron, and the sides of each polygonal region are the edges of the polyhedron. (see p. 726-727) A prism is a polyhedron in which two congruent faces lie in parallel planes and the other faces are bounded by parallelograms. The parallel faces of a prism are the bases of the prism. A prism is usually names after its bases. The faces other than the bases are the lateral faces of a prism. A right prism is one in which the lateral faces are all bounded by rectangles. An oblique prism is one in which some of the lateral faces are not bounded by rectangles. To draw a prism: 1) Draw one of the bases. 2) Draw vertical segments of equal length from each vertex. 3) Connect the bottom endpoints to form the second base. Use dashed segments for edges that cannot be seen. A pyramid is a polyhedron determined by a polygon and a point not in the plane of the polygon. The pyramid consists of the triangular regions determined by the point and each pair of consecutive vertices of the polygon and the polygonal region determined by the polygon.
    [Show full text]
  • VOLUME of POLYHEDRA USING a TETRAHEDRON BREAKUP We
    VOLUME OF POLYHEDRA USING A TETRAHEDRON BREAKUP We have shown in an earlier note that any two dimensional polygon of N sides may be broken up into N-2 triangles T by drawing N-3 lines L connecting every second vertex. Thus the irregular pentagon shown has N=5,T=3, and L=2- With this information, one is at once led to the question-“ How can the volume of any polyhedron in 3D be determined using a set of smaller 3D volume elements”. These smaller 3D eelements are likely to be tetrahedra . This leads one to the conjecture that – A polyhedron with more four faces can have its volume represented by the sum of a certain number of sub-tetrahedra. The volume of any tetrahedron is given by the scalar triple product |V1xV2∙V3|/6, where the three Vs are vector representations of the three edges of the tetrahedron emanating from the same vertex. Here is a picture of one of these tetrahedra- Note that the base area of such a tetrahedron is given by |V1xV2]/2. When this area is multiplied by 1/3 of the height related to the third vector one finds the volume of any tetrahedron given by- x1 y1 z1 (V1xV2 ) V3 Abs Vol = x y z 6 6 2 2 2 x3 y3 z3 , where x,y, and z are the vector components. The next question which arises is how many tetrahedra are required to completely fill a polyhedron? We can arrive at an answer by looking at several different examples. Starting with one of the simplest examples consider the double-tetrahedron shown- It is clear that the entire volume can be generated by two equal volume tetrahedra whose vertexes are placed at [0,0,sqrt(2/3)] and [0,0,-sqrt(2/3)].
    [Show full text]
  • The Mars Pentad Time Pyramids the Quantum Space Time Fractal Harmonic Codex the Pentagonal Pyramid
    The Mars Pentad Time Pyramids The Quantum Space Time Fractal Harmonic Codex The Pentagonal Pyramid Abstract: Early in this author’s labors while attempting to create the original Mars Pentad Time Pyramids document and pyramid drawings, a failure was experienced trying to develop a pentagonal pyramid with some form of tetrahedral geometry. This pentagonal pyramid is now approached again and refined to this tetrahedral criteria, creating tetrahedral angles in the pentagonal pyramid, and pentagonal [54] degree angles in the pentagon base for the pyramid. In the process another fine pentagonal pyramid was developed with pure pentagonal geometries using the value for ancient Egyptian Pyramid Pi = [22 / 7] = [aPi]. Also used is standard modern Pi and modern Phi in one of the two pyramids shown. Introduction: Achieved are two Pentagonal Pyramids: One creates tetrahedral angle [54 .735~] in the Side Angle {not the Side Face Angle}, using a novel height of the value of tetrahedral angle [19 .47122061] / by [5], and then the reverse tetrahedral angle is accomplished with the same tetrahedral [19 .47122061] angle value as the height, but “Harmonic Codexed” to [1 .947122061]! This achievement of using the second height mentioned, proves aspects of the Quantum Space Time Fractal Harmonic Codex. Also used is Height = [2], which replicates the [36] and [54] degree angles in the pentagon base to the Side Angles of the Pentagonal Pyramid. I have come to understand that there is not a “perfect” pentagonal pyramid. No matter what mathematical constants or geometry values used, there will be a slight factor of error inherent in the designs trying to attain tetrahedra.
    [Show full text]
  • Solids, Nets, and Cross Sections
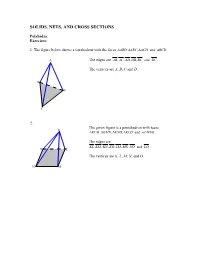
    SOLIDS, NETS, AND CROSS SECTIONS Polyhedra: Exercises: 1. The figure below shows a tetrahedron with the faces ∆ABD,,∆∆ ABC ACD and ∆ BCD . A The edges are AB,,,, AC AD DB BC and DC . The vertices are A, B, C and D, D B C 2. The given figure is a pentahedron with faces K ∆KLM,∆∆∆ KMN , KNO , KLO and . LMNO . The edges are KL,,,,,, KM KN KO LM MN NO and LO . O L The vertices are K, L, M, N, and O. N M Prisms: Exercises (page-4): 1. The right regular octagonal prism has 8 lateral faces, so totally it has 10 faces. It has 24 edges, 8 of them are lateral edges. The prism has 16 vertices. 2. The figure below illustrates an oblique regular triangular prism. It has 5 faces (3 of them are lateral faces), 3 lateral edges and totally 9 edges. The prism has 6 vertices. Pyramids Exercises (page-6): 1. The pentagonal pyramid has 5 lateral faces and thus 6 faces in total. It has 5 lateral edges, 10 edges and 6 vertices. 2. The hexagonal pyramid has 6 lateral faces and 7 faces in total. It has 6 lateral edges, 12 edges and 7 vertices. Nets Exercises: 1. Regular right hexagonal pyramid 2. Rectangular prism 3. Regular right octagonal prism 4. Regular oblique hexagonal prism 5. and so on… 6. Right Cylinder 7. Right Cone Cross sections: Exercises (page-15): 1. i) In the cross section parallel to the base, the cross section is a regular hexagon of the same size as the base.
    [Show full text]
  • Year 6 – Wednesday 24Th June 2020 – Maths
    1 Year 6 – Wednesday 24th June 2020 – Maths Can I identify 3D shapes that have pairs of parallel or perpendicular edges? Parallel – edges that have the same distance continuously between them – parallel edges never meet. Perpendicular – when two edges or faces meet and create a 90o angle. 1 4. 7. 10. 2 5. 8. 11. 3. 6. 9. 12. C1 – Using the shapes above: 1. Name and sort the shapes into: a. Pyramids b. Prisms 2. Draw a table to identify how many faces, edges and vertices each shape has. 3. Write your own geometric definition: a. Prism b. pyramid 4. Which shape is the odd one out? Explain why. C2 – Using the shapes above; 1. Which of the shapes have pairs of parallel edges in: a. All their faces? b. More than one half of the faces? c. One face only? 2. The following shapes have pairs of perpendicular edges. Identify the faces they are in: 2 a. A cube b. A square based pyramid c. A triangular prism d. A cuboid 3. Which shape with straight edges has no perpendicular edges? 4. Which shape has perpendicular edges in the shape but not in any face? C3 – Using the above shapes: 1. How many faces have pairs of parallel edges in: a. A hexagonal pyramid? b. A decagonal (10-sided) based prism? c. A heptagonal based prism? d. Which shape has no face with parallel edges but has parallel edges in the shape? 2. How many faces have perpendicular edges in: a. A pentagonal pyramid b. A hexagonal pyramid c.
    [Show full text]
  • Pentagonal Pyramid
    Chapter 9 Surfaces and Solids Copyright © Cengage Learning. All rights reserved. Pyramids, Area, and 9.2 Volume Copyright © Cengage Learning. All rights reserved. Pyramids, Area, and Volume The solids (space figures) shown in Figure 9.14 below are pyramids. In Figure 9.14(a), point A is noncoplanar with square base BCDE. In Figure 9.14(b), F is noncoplanar with its base, GHJ. (a) (b) Figure 9.14 3 Pyramids, Area, and Volume In each space pyramid, the noncoplanar point is joined to each vertex as well as each point of the base. A solid pyramid results when the noncoplanar point is joined both to points on the polygon as well as to points in its interior. Point A is known as the vertex or apex of the square pyramid; likewise, point F is the vertex or apex of the triangular pyramid. The pyramid of Figure 9.14(b) has four triangular faces; for this reason, it is called a tetrahedron. 4 Pyramids, Area, and Volume The pyramid in Figure 9.15 is a pentagonal pyramid. It has vertex K, pentagon LMNPQ for its base, and lateral edges and Although K is called the vertex of the pyramid, there are actually six vertices: K, L, M, N, P, and Q. Figure 9.15 The sides of the base and are base edges. 5 Pyramids, Area, and Volume All lateral faces of a pyramid are triangles; KLM is one of the five lateral faces of the pentagonal pyramid. Including base LMNPQ, this pyramid has a total of six faces. The altitude of the pyramid, of length h, is the line segment from the vertex K perpendicular to the plane of the base.
    [Show full text]
  • Unit 6 Visualising Solid Shapes(Final)
    • 3D shapes/objects are those which do not lie completely in a plane. • 3D objects have different views from different positions. • A solid is a polyhedron if it is made up of only polygonal faces, the faces meet at edges which are line segments and the edges meet at a point called vertex. • Euler’s formula for any polyhedron is, F + V – E = 2 Where F stands for number of faces, V for number of vertices and E for number of edges. • Types of polyhedrons: (a) Convex polyhedron A convex polyhedron is one in which all faces make it convex. e.g. (1) (2) (3) (4) 12/04/18 (1) and (2) are convex polyhedrons whereas (3) and (4) are non convex polyhedron. (b) Regular polyhedra or platonic solids: A polyhedron is regular if its faces are congruent regular polygons and the same number of faces meet at each vertex. For example, a cube is a platonic solid because all six of its faces are congruent squares. There are five such solids– tetrahedron, cube, octahedron, dodecahedron and icosahedron. e.g. • A prism is a polyhedron whose bottom and top faces (known as bases) are congruent polygons and faces known as lateral faces are parallelograms (when the side faces are rectangles, the shape is known as right prism). • A pyramid is a polyhedron whose base is a polygon and lateral faces are triangles. • A map depicts the location of a particular object/place in relation to other objects/places. The front, top and side of a figure are shown. Use centimetre cubes to build the figure.
    [Show full text]
  • Putting the Icosahedron Into the Octahedron
    Forum Geometricorum Volume 17 (2017) 63–71. FORUM GEOM ISSN 1534-1178 Putting the Icosahedron into the Octahedron Paris Pamfilos Abstract. We compute the dimensions of a regular tetragonal pyramid, which allows a cut by a plane along a regular pentagon. In addition, we relate this construction to a simple construction of the icosahedron and make a conjecture on the impossibility to generalize such sections of regular pyramids. 1. Pentagonal sections The present discussion could be entitled Organizing calculations with Menelaos, and originates from a problem from the book of Sharygin [2, p. 147], in which it is required to construct a pentagonal section of a regular pyramid with quadrangular F J I D T L C K H E M a x A G B U V Figure 1. Pentagonal section of quadrangular pyramid basis. The basis of the pyramid is a square of side-length a and the pyramid is assumed to be regular, i.e. its apex F is located on the orthogonal at the center E of the square at a distance h = |EF| from it (See Figure 1). The exercise asks for the determination of the height h if we know that there is a section GHIJK of the pyramid by a plane which is a regular pentagon. The section is tacitly assumed to be symmetric with respect to the diagonal symmetry plane AF C of the pyramid and defined by a plane through the three points K, G, I. The first two, K and G, lying symmetric with respect to the diagonal AC of the square.
    [Show full text]