DOCSLIB.ORG

The Mars Pentad Time Pyramids the Quantum Space Time Fractal Harmonic Codex the Pentagonal Pyramid

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Mars Pentad Time Pyramids the Quantum Space Time Fractal Harmonic Codex the Pentagonal Pyramid The Mars Pentad Time Pyramids The Quantum Space Time Fractal Harmonic Codex The Pentagonal Pyramid Abstract: Early in this author’s labors while attempting to create the original Mars Pentad Time Pyramids document and pyramid drawings, a failure was experienced trying to develop a pentagonal pyramid with some form of tetrahedral geometry. This pentagonal pyramid is now approached again and refined to this tetrahedral criteria, creating tetrahedral angles in the pentagonal pyramid, and pentagonal [54] degree angles in the pentagon base for the pyramid. In the process another fine pentagonal pyramid was developed with pure pentagonal geometries using the value for ancient Egyptian Pyramid Pi = [22 / 7] = [aPi]. Also used is standard modern Pi and modern Phi in one of the two pyramids shown. Introduction: Achieved are two Pentagonal Pyramids: One creates tetrahedral angle [54 .735~] in the Side Angle {not the Side Face Angle}, using a novel height of the value of tetrahedral angle [19 .47122061] / by [5], and then the reverse tetrahedral angle is accomplished with the same tetrahedral [19 .47122061] angle value as the height, but “Harmonic Codexed” to [1 .947122061]! This achievement of using the second height mentioned, proves aspects of the Quantum Space Time Fractal Harmonic Codex. Also used is Height = [2], which replicates the [36] and [54] degree angles in the pentagon base to the Side Angles of the Pentagonal Pyramid. I have come to understand that there is not a “perfect” pentagonal pyramid. No matter what mathematical constants or geometry values used, there will be a slight factor of error inherent in the designs trying to attain tetrahedra. For instance, the first pyramid can only accomplish a [54 .01] degree angle in the base. The pyramid using ancient Pi will achieve a [54 .0029] degree angle in the base which is quite excellent. The tetrahedral angles however are quite excellent as well, being off exact pure tetrahedral by only a few thousandths of a degree. I consider these to be negligible factors of error in the scope of the beauty achieved in these pentagonal pyramids. The idea then is to attach a pentagonal pyramid of these designs to the faces of the Dodecahedron, to create perfectly unique stellated dodecahedrons. Possibly one should then be able to pack the interior of the dodecahedron with [12] pentagonal pyramids either with tetrahedral geometries or with pentagonal geometry dependent on the height used as above indicated. However the most likely full packing of the interior reduces pyramid height by half, in which case the angles achieved will create quite an unusual planetary time function. In this diagram it is noted that the ancient Pi pentagonal pyramid base will not exact a perfect tetrahedral angle as the pentagonal pyramid using true Pi and true Phi as constructs in the formation. This diagram is fairly self explanatory: There are [3] different heights used, [19 .47122061 / by 5], [1 .947122061], and [2]. The flaw is in the angle [x] which is [54 .01] degrees, giving me a [540.1] degree pentagon, with a factor of error of [2 / 10,000] in the base. The tetrahedral angles resultant however, are virtually perfect, and have error only in the ten thousandths of a single degree. Earlier in the introduction was mentioned the packing of the interior of the dodecahedron dependent on the inner height of the packed pentagonal pyramids. If the interior pentagonal pyramid heights are [1], then the Side Angles are [2] and [70], and the Side Face Angles are [24 .170] and [65 .8295]. Curiously if you square both those values you come excruciatingly close to standard astronomical planetary time lines: [24 .170~] squared = [584.2] or the [584] Venus synod, [65 .8295] squared = [4333 .524] or the Jupiter sidereal [4332]. Modern Phi value is used as [1 .618033989] and Phi squared as [2 .618033989]. Height used is [2]. Angle [x] is the pentagonal base angle =[54.00 293595]. Angle [z] is the pentagonal pyramid Side Angle = [35.99 807831] = [36] degrees. As you can see from the drawing lower right corner, even ancient Phi can be used in the process though not as perfect in the pentagon base, but perfectly in the Side Angle of the pyramid itself. If the interior packing is height [1] for the interior pentagonal pyramids, then the angles are similar as in the last pyramid and the same number anomaly occurs: Angle [24 .17910647] squared = [584 .629] closer to my [585] Venus sidereal I use and, Opposite Angle [65 .82089353] squared = [4332 .390026] ON THE BUTTON for standard western astronomical sidereal of Jupiter! This below is a preview of the final upcoming Conclusion! Of the Mars Pentad Time Pyramids Part 2, And the Quantum Space Time Fractal Harmonic Codex. The Great Pyramid of Giza in feet, with a comparison pyramid using [aPi]: The [336] value is a high physics E8 value recently studied by the author. This will all be explained and reviewed in the Conclusion pdf, along with the Leedskalnin numbers in the Harmonic Codex, the sidereal of Planet X and more. Cheers! PS, Sqrt [8] / Pi = tangent [41.997] degrees, Sqrt [14] / Pi = tangent [49 .98] degrees. {C} Vic Showell Dec 11 2008 The Stellated Dodecahedron by Magnus Wenninger. Dodecahedron with pentagonal pyramids attached. http://www.theweebsite.com/polyhedra/pmftc/fig22p.jpg http://www.theweebsite.com/polyhedra/pmftc/pmftc4.html .
Load more

Recommended publications
  • Build a Tetrahedral Kite
    Aeronautics Research Mission Directorate Build a Tetrahedral Kite Suggested Grades: 8-12 Activity Overview Time: 90-120 minutes In this activity, you will build a tetrahedral kite from Materials household supplies. • 24 straws (8 inches or less) - NOTE: The straws need to be Steps straight and the same length. If only flexible straws are available, 1. Cut a length of yarn/string 4 feet long. then cut off the flexible portion. • Two or three large spools of 2. Take six straws and place them on a flat surface. cotton string or yarn (approximately 100 feet total) 3. Use your piece of string to join three straws • Scissors together in a triangular shape. On the side where • Hot glue gun and hot glue sticks the two strings are extending from it, one end • Ruler or dowel rod for kite bridle should be approximately 20 inches long, and the • Four pieces of tissue paper (24 x other should be approximately 4 inches long. 18 inches or larger) See Figure 1. • All-purpose glue stick Figure 1 4. Tie these two ends of the string tightly together. Make sure there is no room for the triangle to wiggle. 5. The three straws should form a tight triangle. 6. Cut another 4-inch piece of string. 7. Take one end of the 4-inch string, and tie that end to a corner of the triangle that does not have the string ends extending from it. Figure 2. 8. Add two more straws onto the longest piece of string. 9. Next, take the string that holds the two additional straws and tie it to the end of one of the 4-inch strings to make another tight triangle.
    [Show full text]
  • THE GEOMETRY of PYRAMIDS One of the More Interesting Solid
    THE GEOMETRY OF PYRAMIDS One of the more interesting solid structures which has fascinated individuals for thousands of years going all the way back to the ancient Egyptians is the pyramid. It is a structure in which one takes a closed curve in the x-y plane and connects straight lines between every point on this curve and a fixed point P above the centroid of the curve. Classical pyramids such as the structures at Giza have square bases and lateral sides close in form to equilateral triangles. When the closed curve becomes a circle one obtains a cone and this cone becomes a cylindrical rod when point P is moved to infinity. It is our purpose here to discuss the properties of all N sided pyramids including their volume and surface area using only elementary calculus and geometry. Our starting point will be the following sketch- The base represents a regular N sided polygon with side length ‘a’ . The angle between neighboring radial lines r (shown in red) connecting the polygon vertices with its centroid is θ=2π/N. From this it follows, by the law of cosines, that the length r=a/sqrt[2(1- cos(θ))] . The area of the iscosolis triangle of sides r-a-r is- a a 2 a 2 1 cos( ) A r 2 T 2 4 4 (1 cos( ) From this we have that the area of the N sided polygon and hence the pyramid base will be- 2 2 1 cos( ) Na A N base 2 4 1 cos( ) N 2 It readily follows from this result that a square base N=4 has area Abase=a and a hexagon 2 base N=6 yields Abase= 3sqrt(3)a /2.
    [Show full text]
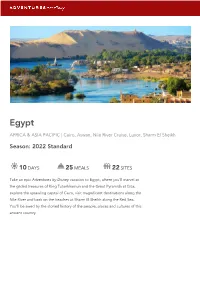
  • 2022 Standard
    EGYPT Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Egypt AFRICA & ASIA PACIFIC | Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Season: 2022 Standard 10 DAYS 25 MEALS 22 SITES Take an epic Adventures by Disney vacation to Egypt, where you’ll marvel at the gilded treasures of King Tutankhamun and the Great Pyramids at Giza, explore the sprawling capital of Cairo, visit magnificent destinations along the Nile River and bask on the beaches at Sharm El Sheikh along the Red Sea. You’ll be awed by the storied history of the people, places and cultures of this ancient country. EGYPT Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Trip Overview 10 DAYS / 9 NIGHTS ACCOMMODATIONS 5 LOCATIONS The Nile Ritz-Carlton, Cairo Cairo, Aswan, Nile River M/S Tulip Cruise, Luxor, Sharm El Sheikh Coral Sea Sensatori Resort AGES FLIGHT INFORMATION 25 MEALS Minimum Age: 6 Arrive: Cairo International 9 Breakfasts, 8 Lunches, 8 Suggested Age: 8+ Airport (CAI) Dinners Adult Exclusive: Ages 18+ Return: Cairo International Airport (CAI) All Internal Flights Included EGYPT Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh DAY 1 CAIRO Activities Highlights: No Meals Included Arrive in Cairo The Nile Ritz-Carlton, Cairo Arrive in Cairo ‘Ahlaan Wasahlaan Bikum! Upon your arrival at Cairo International Airport, Adventures by Disney Guests will be escorted to a VIP lounge while your passports are processed and your luggage is reclaimed. You will then be taken to your waiting vehicles for transfer to the hotel, The Nile Ritz-Carlton, Cairo. The Nile Ritz-Carlton, Cairo Bask in the elegance that surrounds you in this luxury hotel that offers world-class services and amenities that are fit for a pharaoh.
    [Show full text]
  • Math 366 Lecture Notes Section 11.4 – Geometry in Three Dimensions
    Section 11-4 Math 366 Lecture Notes Section 11.4 – Geometry in Three Dimensions Simple Closed Surfaces A simple closed surface has exactly one interior, no holes, and is hollow. A sphere is the set of all points at a given distance from a given point, the center . A sphere is a simple closed surface. A solid is a simple closed surface with all interior points. (see p. 726) A polyhedron is a simple closed surface made up of polygonal regions, or faces . The vertices of the polygonal regions are the vertices of the polyhedron, and the sides of each polygonal region are the edges of the polyhedron. (see p. 726-727) A prism is a polyhedron in which two congruent faces lie in parallel planes and the other faces are bounded by parallelograms. The parallel faces of a prism are the bases of the prism. A prism is usually names after its bases. The faces other than the bases are the lateral faces of a prism. A right prism is one in which the lateral faces are all bounded by rectangles. An oblique prism is one in which some of the lateral faces are not bounded by rectangles. To draw a prism: 1) Draw one of the bases. 2) Draw vertical segments of equal length from each vertex. 3) Connect the bottom endpoints to form the second base. Use dashed segments for edges that cannot be seen. A pyramid is a polyhedron determined by a polygon and a point not in the plane of the polygon. The pyramid consists of the triangular regions determined by the point and each pair of consecutive vertices of the polygon and the polygonal region determined by the polygon.
    [Show full text]
  • VOLUME of POLYHEDRA USING a TETRAHEDRON BREAKUP We
    VOLUME OF POLYHEDRA USING A TETRAHEDRON BREAKUP We have shown in an earlier note that any two dimensional polygon of N sides may be broken up into N-2 triangles T by drawing N-3 lines L connecting every second vertex. Thus the irregular pentagon shown has N=5,T=3, and L=2- With this information, one is at once led to the question-“ How can the volume of any polyhedron in 3D be determined using a set of smaller 3D volume elements”. These smaller 3D eelements are likely to be tetrahedra . This leads one to the conjecture that – A polyhedron with more four faces can have its volume represented by the sum of a certain number of sub-tetrahedra. The volume of any tetrahedron is given by the scalar triple product |V1xV2∙V3|/6, where the three Vs are vector representations of the three edges of the tetrahedron emanating from the same vertex. Here is a picture of one of these tetrahedra- Note that the base area of such a tetrahedron is given by |V1xV2]/2. When this area is multiplied by 1/3 of the height related to the third vector one finds the volume of any tetrahedron given by- x1 y1 z1 (V1xV2 ) V3 Abs Vol = x y z 6 6 2 2 2 x3 y3 z3 , where x,y, and z are the vector components. The next question which arises is how many tetrahedra are required to completely fill a polyhedron? We can arrive at an answer by looking at several different examples. Starting with one of the simplest examples consider the double-tetrahedron shown- It is clear that the entire volume can be generated by two equal volume tetrahedra whose vertexes are placed at [0,0,sqrt(2/3)] and [0,0,-sqrt(2/3)].
    [Show full text]
  • EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh
    EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Egypt – Private Adventure AFRICA & ASIA PACIFIC | Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Season: 2021 10 DAYS 25 MEALS 22 SITES Take an epic Adventures by Disney Private Adventure to Egypt, where you’ll marvel at the gilded treasures of King Tutankhamun and the Great Pyramids at Giza, explore the sprawling capital of Cairo, visit magnificent destinations along the Nile River and bask on the beaches at Sharm El Sheikh along the Red Sea. You’ll be awed by the storied history of the people, places and cultures of this ancient country. EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Trip Overview 10 DAYS / 9 NIGHTS ACCOMMODATIONS 5 LOCATIONS The Nile Ritz-Carlton, Cairo Cairo, Aswan, Nile River M/S Tulip Cruise, Luxor, Sharm El Sheikh Coral Sea Sensatori Resort AGES FLIGHT INFORMATION 25 MEALS Minimum Age: None Arrive: Cairo International 9 Breakfasts, 8 Lunches, 8 Airport (CAI) Dinners Return: Cairo International Airport (CAI) All Internal Flights Included EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh DAY 1 CAIRO Activities Highlights: No Meals Included Arrive in Cairo The Nile Ritz-Carlton, Cairo Arrive in Cairo ‘Ahlaan Wasahlaan Bikum! Upon your arrival at Cairo International Airport, Adventures by Disney Guests will be escorted to a VIP lounge while your visa and passports are processed and your luggage is reclaimed. You will then be taken to your waiting vehicle for transfer to the hotel, The Nile Ritz-Carlton, Cairo. Note: A visa is provided to each Guest upon arrival and does not need to be secured in advance of departing for Egypt.
    [Show full text]
  • Pentagonal Pyramid
    Chapter 9 Surfaces and Solids Copyright © Cengage Learning. All rights reserved. Pyramids, Area, and 9.2 Volume Copyright © Cengage Learning. All rights reserved. Pyramids, Area, and Volume The solids (space figures) shown in Figure 9.14 below are pyramids. In Figure 9.14(a), point A is noncoplanar with square base BCDE. In Figure 9.14(b), F is noncoplanar with its base, GHJ. (a) (b) Figure 9.14 3 Pyramids, Area, and Volume In each space pyramid, the noncoplanar point is joined to each vertex as well as each point of the base. A solid pyramid results when the noncoplanar point is joined both to points on the polygon as well as to points in its interior. Point A is known as the vertex or apex of the square pyramid; likewise, point F is the vertex or apex of the triangular pyramid. The pyramid of Figure 9.14(b) has four triangular faces; for this reason, it is called a tetrahedron. 4 Pyramids, Area, and Volume The pyramid in Figure 9.15 is a pentagonal pyramid. It has vertex K, pentagon LMNPQ for its base, and lateral edges and Although K is called the vertex of the pyramid, there are actually six vertices: K, L, M, N, P, and Q. Figure 9.15 The sides of the base and are base edges. 5 Pyramids, Area, and Volume All lateral faces of a pyramid are triangles; KLM is one of the five lateral faces of the pentagonal pyramid. Including base LMNPQ, this pyramid has a total of six faces. The altitude of the pyramid, of length h, is the line segment from the vertex K perpendicular to the plane of the base.
    [Show full text]
  • Unit 6 Visualising Solid Shapes(Final)
    • 3D shapes/objects are those which do not lie completely in a plane. • 3D objects have different views from different positions. • A solid is a polyhedron if it is made up of only polygonal faces, the faces meet at edges which are line segments and the edges meet at a point called vertex. • Euler’s formula for any polyhedron is, F + V – E = 2 Where F stands for number of faces, V for number of vertices and E for number of edges. • Types of polyhedrons: (a) Convex polyhedron A convex polyhedron is one in which all faces make it convex. e.g. (1) (2) (3) (4) 12/04/18 (1) and (2) are convex polyhedrons whereas (3) and (4) are non convex polyhedron. (b) Regular polyhedra or platonic solids: A polyhedron is regular if its faces are congruent regular polygons and the same number of faces meet at each vertex. For example, a cube is a platonic solid because all six of its faces are congruent squares. There are five such solids– tetrahedron, cube, octahedron, dodecahedron and icosahedron. e.g. • A prism is a polyhedron whose bottom and top faces (known as bases) are congruent polygons and faces known as lateral faces are parallelograms (when the side faces are rectangles, the shape is known as right prism). • A pyramid is a polyhedron whose base is a polygon and lateral faces are triangles. • A map depicts the location of a particular object/place in relation to other objects/places. The front, top and side of a figure are shown. Use centimetre cubes to build the figure.
    [Show full text]
  • Putting the Icosahedron Into the Octahedron
    Forum Geometricorum Volume 17 (2017) 63–71. FORUM GEOM ISSN 1534-1178 Putting the Icosahedron into the Octahedron Paris Pamfilos Abstract. We compute the dimensions of a regular tetragonal pyramid, which allows a cut by a plane along a regular pentagon. In addition, we relate this construction to a simple construction of the icosahedron and make a conjecture on the impossibility to generalize such sections of regular pyramids. 1. Pentagonal sections The present discussion could be entitled Organizing calculations with Menelaos, and originates from a problem from the book of Sharygin [2, p. 147], in which it is required to construct a pentagonal section of a regular pyramid with quadrangular F J I D T L C K H E M a x A G B U V Figure 1. Pentagonal section of quadrangular pyramid basis. The basis of the pyramid is a square of side-length a and the pyramid is assumed to be regular, i.e. its apex F is located on the orthogonal at the center E of the square at a distance h = |EF| from it (See Figure 1). The exercise asks for the determination of the height h if we know that there is a section GHIJK of the pyramid by a plane which is a regular pentagon. The section is tacitly assumed to be symmetric with respect to the diagonal symmetry plane AF C of the pyramid and defined by a plane through the three points K, G, I. The first two, K and G, lying symmetric with respect to the diagonal AC of the square.
    [Show full text]
  • 2D and 3D Shapes.Pdf
    & • Anchor 2 - D Charts • Flash Cards 3 - D • Shape Books • Practice Pages rd Shapesfor 3 Grade by Carrie Lutz T hank you for purchasing!!! Check out my store: http://www.teacherspayteachers.com/Store/Carrie-Lutz-6 Follow me for notifications of freebies, sales and new arrivals! Visit my BLOG for more Free Stuff! Read My Blog Post about Teaching 3 Dimensional Figures Correctly Credits: Carrie Lutz©2016 2D Shape Bank 3D Shape Bank 3 Sided 5 Sided Prisms triangular prism cube rectangular prism triangle pentagon 4 Sided rectangle square pentagonal prism hexagonal prism octagonal prism Pyramids rhombus trapezoid 6 Sided 8 Sided rectangular square triangular pyramid pyramid pyramid Carrie LutzCarrie CarrieLutz pentagonal hexagonal © hexagon octagon © 2016 pyramid pyramid 2016 Curved Shapes CURVED SOLIDS oval circle sphere cone cylinder Carrie Lutz©2016 Carrie Lutz©2016 Name _____________________ Side Sort Date _____________________ Cut out the shapes below and glue them in the correct column. More than 4 Less than 4 Exactly 4 Carrie Lutz©2016 Name _____________________ Name the Shapes Date _____________________ 1. Name the Shape. 2. Name the Shape. 3. Name the Shape. ____________________________________ ____________________________________ ____________________________________ 4. Name the Shape. 5. Name the Shape. 6. Name the Shape. ____________________________________ ____________________________________ ____________________________________ 4. Name the Shape. 5. Name the Shape. 6. Name the Shape. ____________________________________ ____________________________________ ____________________________________ octagon circle square rhombus triangle hexagon pentagon rectangle trapezoid Carrie Lutz©2016 Faces, Edges, Vertices Name _____________________ and Date _____________________ 1. Name the Shape. 2. Name the Shape. 3. Name the Shape. ____________________________________ ____________________________________ ____________________________________ _____ faces _____ faces _____ faces _____Edges _____Edges _____Edges _____Vertices _____Vertices _____Vertices 4.
    [Show full text]
  • Seven Wonders Time:​ 30 Minutes Level:​ Beginner
    Lesson Five: Seven Wonders Time:​ 30 minutes Level:​ Beginner Intro The Seven Wonders of the Ancient World were architectural feats recorded by ancient historians, writers and scholars in the western world - the list is limited geographically to the mediterranean, the centre of ancient western civilization. The only remaining wonder in the present day is the Great Pyramid of Giza, which is also the oldest. The rest have all been destroyed by weather, war or nature. Today we’re going to learn a little bit about each one: The Great Pyramid of Giza The pyramids are, in many ways, the most famous ancient wonder of the world. Whether that’s attributed to their mystery, incredible feat of construction, or their sole survival (out of all of the ancient wonders) into the modern era, all marvel at their magnificence. The Great Pyramid of Giza was constructed around 2589-2566 B.C. during the reign of Pharaoh Khufu. It stood about 147 meters tall and its base was approximately 230 meters in length. The second pyramid was created for Khufu’s son, Pharaoh Khafre, in 2558-2532 B.C. Within the pyramid’s complex at Giza was the largest statue in the world at that time, known as the Great Sphinx (a man’s head on a lion’s body), standing 240 feet long and 66 feet tall. The last pyramid was built around 2532-2503 B.C. for Khafre’s son, Pharaoh Menkaure. It was the shortest of the three pyramids in this ancient wonder, standing at only 216 feet tall. It took over 2.3 million blocks of limestone, 100,000 men, and 20 years to construct the greatest architectural achievement in the ancient world.
    [Show full text]
  • Decoding the Last Supper
    HOUSE OF TRUTH | TOTUUDEN TALO Decoding the Last Supper The Great Year and Men as Gods House of Truth | www.houseoftruth.education 21.6.2013 Table of Contents Introduction ....................................................................................................................................................... 2 The Last Supper and the Great Year .................................................................................................................. 3 36 engravings on the roof ............................................................................................................................. 4 Elements of the Last Supper .......................................................................................................................... 5 Hands of Christ .............................................................................................................................................. 6 The Lesser Conclusion ................................................................................................................................... 7 Men as Gods in the Last Supper ........................................................................................................................ 8 Roman trio of gods ........................................................................................................................................ 9 Evidence number 153 .................................................................................................................................
    [Show full text]