Originality Statement
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Islamic Geometric Ornaments in Istanbul
►SKETCH 2 CONSTRUCTIONS OF REGULAR POLYGONS Regular polygons are the base elements for constructing the majority of Islamic geometric ornaments. Of course, in Islamic art there are geometric ornaments that may have different genesis, but those that can be created from regular polygons are the most frequently seen in Istanbul. We can also notice that many of the Islamic geometric ornaments can be recreated using rectangular grids like the ornament in our first example. Sometimes methods using rectangular grids are much simpler than those based or regular polygons. Therefore, we should not omit these methods. However, because methods for constructing geometric ornaments based on regular polygons are the most popular, we will spend relatively more time explor- ing them. Before, we start developing some concrete constructions it would be worthwhile to look into a few issues of a general nature. As we have no- ticed while developing construction of the ornament from the floor in the Sultan Ahmed Mosque, these constructions are not always simple, and in order to create them we need some knowledge of elementary geometry. On the other hand, computer programs for geometry or for computer graphics can give us a number of simpler ways to develop geometric fig- ures. Some of them may not require any knowledge of geometry. For ex- ample, we can create a regular polygon with any number of sides by rotat- ing a point around another point by using rotations 360/n degrees. This is a very simple task if we use a computer program and the only knowledge of geometry we need here is that the full angle is 360 degrees. -

Le Corbusier Charles-Édouard Jeanneret-Gris
Le Corbusier Charles-Édouard Jeanneret-Gris Portrait on Swiss ten francs banknote Personal information Name: Charles-Édouard Jeanneret-Gris Nationality: Swiss / French Birth date: October 6, 1887 Birth place: La Chaux-de-Fonds, Switzerland Date of death: August 27, 1965 (aged 77) Place of death: Roquebrune-Cap-Martin, France 1 Created with novaPDF Printer (www.novaPDF.com). Please register to remove this message. Major buildings and projects The Open Hand Monument is one of numerous projects in Chandigarh, India designed by Le Corbusier 1905 - Villa Fallet, La Chaux-de-Fonds, Switzerland 1912 - Villa Jeanneret-Perret, La Chaux-de-Fonds [1] 1916 - Villa Schwob, La Chaux-de-Fonds 1923 - Villa LaRoche/Villa Jeanneret, Paris 1924 - Pavillon de L'Esprit Nouveau, Paris (destroyed) 1924 - Quartiers Modernes Frugès, Pessac, France 1925 - Villa Jeanneret, Paris 1926 - Villa Cook, Boulogne-sur-Seine, France 1927 - Villas at Weissenhof Estate, Stuttgart, Germany 1928 - Villa Savoye, Poissy-sur-Seine, France 1929 - Armée du Salut, Cité de Refuge, Paris 1930 - Pavillon Suisse, Cité Universitaire, Paris 1930 - Maison Errazuriz, Chile 1931 - Palace of the Soviets, Moscow, USSR (project) 1931 - Immeuble Clarté, Geneva, Switzerland 1933 - Tsentrosoyuz, Moscow, USSR 1936 - Palace of Ministry of National Education and Public Health, Rio de Janeiro 1938 - The "Cartesian" sky-scraper (project) 1945 - Usine Claude et Duval, Saint-Dié-des-Vosges, France 1947-1952 - Unité d'Habitation, Marseille, France 1948 - Curutchet House, La Plata, Argentina 1949-1952 - United Nations headquarters, New York City (project) 1950-1954 - Chapelle Notre Dame du Haut, Ronchamp, France 1951 - Cabanon Le Corbusier, Roquebrune-Cap-Martin 2 Created with novaPDF Printer (www.novaPDF.com). -

Polygon Review and Puzzlers in the Above, Those Are Names to the Polygons: Fill in the Blank Parts. Names: Number of Sides
Polygon review and puzzlers ÆReview to the classification of polygons: Is it a Polygon? Polygons are 2-dimensional shapes. They are made of straight lines, and the shape is "closed" (all the lines connect up). Polygon Not a Polygon Not a Polygon (straight sides) (has a curve) (open, not closed) Regular polygons have equal length sides and equal interior angles. Polygons are named according to their number of sides. Name of Degree of Degree of triangle total angles regular angles Triangle 180 60 In the above, those are names to the polygons: Quadrilateral 360 90 fill in the blank parts. Pentagon Hexagon Heptagon 900 129 Names: number of sides: Octagon Nonagon hendecagon, 11 dodecagon, _____________ Decagon 1440 144 tetradecagon, 13 hexadecagon, 15 Do you see a pattern in the calculation of the heptadecagon, _____________ total degree of angles of the polygon? octadecagon, _____________ --- (n -2) x 180° enneadecagon, _____________ icosagon 20 pentadecagon, _____________ These summation of angles rules, also apply to the irregular polygons, try it out yourself !!! A point where two or more straight lines meet. Corner. Example: a corner of a polygon (2D) or of a polyhedron (3D) as shown. The plural of vertex is "vertices” Test them out yourself, by drawing diagonals on the polygons. Here are some fun polygon riddles; could you come up with the answer? Geometry polygon riddles I: My first is in shape and also in space; My second is in line and also in place; My third is in point and also in line; My fourth in operation but not in sign; My fifth is in angle but not in degree; My sixth is in glide but not symmetry; Geometry polygon riddles II: I am a polygon all my angles have the same measure all my five sides have the same measure, what general shape am I? Geometry polygon riddles III: I am a polygon. -
2022 Standard
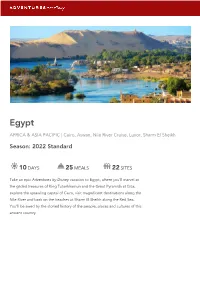
EGYPT Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Egypt AFRICA & ASIA PACIFIC | Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Season: 2022 Standard 10 DAYS 25 MEALS 22 SITES Take an epic Adventures by Disney vacation to Egypt, where you’ll marvel at the gilded treasures of King Tutankhamun and the Great Pyramids at Giza, explore the sprawling capital of Cairo, visit magnificent destinations along the Nile River and bask on the beaches at Sharm El Sheikh along the Red Sea. You’ll be awed by the storied history of the people, places and cultures of this ancient country. EGYPT Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Trip Overview 10 DAYS / 9 NIGHTS ACCOMMODATIONS 5 LOCATIONS The Nile Ritz-Carlton, Cairo Cairo, Aswan, Nile River M/S Tulip Cruise, Luxor, Sharm El Sheikh Coral Sea Sensatori Resort AGES FLIGHT INFORMATION 25 MEALS Minimum Age: 6 Arrive: Cairo International 9 Breakfasts, 8 Lunches, 8 Suggested Age: 8+ Airport (CAI) Dinners Adult Exclusive: Ages 18+ Return: Cairo International Airport (CAI) All Internal Flights Included EGYPT Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh DAY 1 CAIRO Activities Highlights: No Meals Included Arrive in Cairo The Nile Ritz-Carlton, Cairo Arrive in Cairo ‘Ahlaan Wasahlaan Bikum! Upon your arrival at Cairo International Airport, Adventures by Disney Guests will be escorted to a VIP lounge while your passports are processed and your luggage is reclaimed. You will then be taken to your waiting vehicles for transfer to the hotel, The Nile Ritz-Carlton, Cairo. The Nile Ritz-Carlton, Cairo Bask in the elegance that surrounds you in this luxury hotel that offers world-class services and amenities that are fit for a pharaoh. -

Le Corbusier and His Contemporaries
1 April 2002 Art History W36456 Important announcements: Monday April 8th I cannot prepare class ahead of time, we will instead view a series of films by and about Le Corbusier and his contemporaries. To make up for the missed lecture there will be an extra concluding class of the course on Weds. May 8th at the usual time and in this room. Please mark your calendars. As we are now behind the course will conclude with 1965 and the examination will include all material through topic 25. A new course on Post War Architecture, the third part of the survey then, will be introduced in 2003-4. Le Corbusier: Architecture or Revolution (architecture and urbanism to 1930) Charles-Edouard Jeanneret (takes name Le Corbusier in the 1920s) b. 1887 La Chaux-de-Fonds, Switzerland, died Roquebrunne (Riveria) 1965; architect in Paris from 1917 on. Arts School in La Chaux de Fonds and influence of Charles L’Eplattenier 1905-06 Villa Fallet, La Chaux de Fonds 1908-9 in Paris with Perret and meets Tony Garnier 1910 with Theodore Fischer in Munich and with Behrens in Berlin/Potsdam 1908 Villa Jacquemet, La Chaux de Fonds 1914-16 Villa Schwob (Maison Turque), La Chaux-de-Fonds (first concrete frame) 1914 Domino (Dom-Ino) project with Max Dubois 1918 publishes Après le Cubisme with Amedée Ozenfant 1920 first issue of the magazine L’Esprit Nouveau 1923 Vers une Architecture (translated into English in 1927 as Towards a new Architecture) 1922 Salone d’Automne Paris, he exhibits the Citrohan House and the Ville de 3 Millions d’Habitants 1922 Ozenfant Studio, Paris -

Le Corbusier Architecture Tour of Switzerland
Le Corbusier architecture tour of Switzerland http://www.travelbite.co.uk/printerfriendly.aspx?itemid=1252859 Le Corbusier architecture tour of Switzerland Friday, 05 Dec 2008 00:00 Considered by many to be the most important architect of the 20th century, Charles- Édouard Jeanneret-Gris – who chose to be known as Le Corbusier – was the driving force behind the International style. Also known as Modern architecture, the movement stressed the importance of form and the elimination of ornament - values explored by Le Corbusier over a career spanning five decades. His Five Points – first expressed in the L'Esprit Nouveau - epitomise the style, and allowed his work to spread from his native Switzerland around the world, including developments in Le Maison Blanche (credit: Eveline France, India, Russia, Chile, Germany and even Iraq. Perroud) Born in La Chaux-de-Fonds, Switzerland, Le Corbusier began his career in his home town with La Maison Blanche – a very personal project for his parents, completed in 1912. It is one of a number of Le Corbusier buildings still standing in Switzerland, and here travelbite.co.uk takes a look at what is on offer to visitors as they explore his native land. La Chaux-de-Fonds Le Maison Blanche was the first independent project completed by Le Corbusier, and draws on his experience in Paris as a student of Auguste Perret and Peter Behrens in Berlin. Situated in his home town of La Chaux-de-Fonds, guests are invited to explore one of the early works of the aspiring architect, who had not yet taken the name Le Corbusier. -

Formulas Involving Polygons - Lesson 7-3
you are here > Class Notes – Chapter 7 – Lesson 7-3 Formulas Involving Polygons - Lesson 7-3 Here’s today’s warmup…don’t forget to “phone home!” B Given: BD bisects ∠PBQ PD ⊥ PB QD ⊥ QB M Prove: BD is ⊥ bis. of PQ P Q D Statements Reasons Honors Geometry Notes Today, we started by learning how polygons are classified by their number of sides...you should already know a lot of these - just make sure to memorize the ones you don't know!! Sides Name 3 Triangle 4 Quadrilateral 5 Pentagon 6 Hexagon 7 Heptagon 8 Octagon 9 Nonagon 10 Decagon 11 Undecagon 12 Dodecagon 13 Tridecagon 14 Tetradecagon 15 Pentadecagon 16 Hexadecagon 17 Heptadecagon 18 Octadecagon 19 Enneadecagon 20 Icosagon n n-gon Baroody Page 2 of 6 Honors Geometry Notes Next, let’s look at the diagonals of polygons with different numbers of sides. By drawing as many diagonals as we could from one diagonal, you should be able to see a pattern...we can make n-2 triangles in a n-sided polygon. Given this information and the fact that the sum of the interior angles of a polygon is 180°, we can come up with a theorem that helps us to figure out the sum of the measures of the interior angles of any n-sided polygon! Baroody Page 3 of 6 Honors Geometry Notes Next, let’s look at exterior angles in a polygon. First, consider the exterior angles of a pentagon as shown below: Note that the sum of the exterior angles is 360°. -

Le Corbusier's Cité De Refuge
DOI: http://dx.doi.org/10.4995/LC2015.2015.796 Le Corbusier’s Cité de Refuge: historical & technological performance of the air exacte L.M. Diaz, R. Southall School of Arts, Design and Media, University of Brighton Abstract: Despite a number of attempts by Le Corbusier to implement the combination of ‘respiration exacte’ with the ‘mur neutralisant’ he was never able to test the viability of his environmental concepts in a realised building. The Cité de Refuge, which was built with a more conventional heating system and single glazed facade, is however unique in that unlike the other potential candidates for the implementation of these systems, the building, as built, retained a key design feature, i.e. the hermetically sealed skin, which ultimately contributed to the building’s now infamous failure. It is commonly argued that Le Corbusier, however, abandoned these comprehensive technical solutions in favour of a more passive approach, but it is less well understood to what extent technical failures influenced this shift. If these failures were one of the drivers for this change, how the building may have performed with the ‘respiration exacte’ and ‘mur neutralisant’ systems becomes of interest. Indeed, how their performance may have been improved with Le Corbusier's later modification of a brise-soleil offers an alternative hypothetical narrative for his relationship to technical and passive design methodologies. Keywords: environment, technology, performance, history, Cité de Refuge. 1. Introduction There are two technical building concepts that represent, perhaps more than any others Le Corbusier’s early drive to find comprehensive and exclusively mechanical approaches to the heating and ventilation of modern buildings: a) the mur neutralisant, a double-skin glazed wall with conditioned air circulated within the cavity to moderate heat exchange between the interior and exterior, and b) the respiration exacte, a mechanical ventilation system for providing conditioned air to interior spaces at a constant temperature of 18˚C. -

EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh
EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Egypt – Private Adventure AFRICA & ASIA PACIFIC | Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Season: 2021 10 DAYS 25 MEALS 22 SITES Take an epic Adventures by Disney Private Adventure to Egypt, where you’ll marvel at the gilded treasures of King Tutankhamun and the Great Pyramids at Giza, explore the sprawling capital of Cairo, visit magnificent destinations along the Nile River and bask on the beaches at Sharm El Sheikh along the Red Sea. You’ll be awed by the storied history of the people, places and cultures of this ancient country. EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Trip Overview 10 DAYS / 9 NIGHTS ACCOMMODATIONS 5 LOCATIONS The Nile Ritz-Carlton, Cairo Cairo, Aswan, Nile River M/S Tulip Cruise, Luxor, Sharm El Sheikh Coral Sea Sensatori Resort AGES FLIGHT INFORMATION 25 MEALS Minimum Age: None Arrive: Cairo International 9 Breakfasts, 8 Lunches, 8 Airport (CAI) Dinners Return: Cairo International Airport (CAI) All Internal Flights Included EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh DAY 1 CAIRO Activities Highlights: No Meals Included Arrive in Cairo The Nile Ritz-Carlton, Cairo Arrive in Cairo ‘Ahlaan Wasahlaan Bikum! Upon your arrival at Cairo International Airport, Adventures by Disney Guests will be escorted to a VIP lounge while your visa and passports are processed and your luggage is reclaimed. You will then be taken to your waiting vehicle for transfer to the hotel, The Nile Ritz-Carlton, Cairo. Note: A visa is provided to each Guest upon arrival and does not need to be secured in advance of departing for Egypt. -

The Mars Pentad Time Pyramids the Quantum Space Time Fractal Harmonic Codex the Pentagonal Pyramid
The Mars Pentad Time Pyramids The Quantum Space Time Fractal Harmonic Codex The Pentagonal Pyramid Abstract: Early in this author’s labors while attempting to create the original Mars Pentad Time Pyramids document and pyramid drawings, a failure was experienced trying to develop a pentagonal pyramid with some form of tetrahedral geometry. This pentagonal pyramid is now approached again and refined to this tetrahedral criteria, creating tetrahedral angles in the pentagonal pyramid, and pentagonal [54] degree angles in the pentagon base for the pyramid. In the process another fine pentagonal pyramid was developed with pure pentagonal geometries using the value for ancient Egyptian Pyramid Pi = [22 / 7] = [aPi]. Also used is standard modern Pi and modern Phi in one of the two pyramids shown. Introduction: Achieved are two Pentagonal Pyramids: One creates tetrahedral angle [54 .735~] in the Side Angle {not the Side Face Angle}, using a novel height of the value of tetrahedral angle [19 .47122061] / by [5], and then the reverse tetrahedral angle is accomplished with the same tetrahedral [19 .47122061] angle value as the height, but “Harmonic Codexed” to [1 .947122061]! This achievement of using the second height mentioned, proves aspects of the Quantum Space Time Fractal Harmonic Codex. Also used is Height = [2], which replicates the [36] and [54] degree angles in the pentagon base to the Side Angles of the Pentagonal Pyramid. I have come to understand that there is not a “perfect” pentagonal pyramid. No matter what mathematical constants or geometry values used, there will be a slight factor of error inherent in the designs trying to attain tetrahedra. -

Geometrygeometry
Park Forest Math Team Meet #3 GeometryGeometry Self-study Packet Problem Categories for this Meet: 1. Mystery: Problem solving 2. Geometry: Angle measures in plane figures including supplements and complements 3. Number Theory: Divisibility rules, factors, primes, composites 4. Arithmetic: Order of operations; mean, median, mode; rounding; statistics 5. Algebra: Simplifying and evaluating expressions; solving equations with 1 unknown including identities Important Information you need to know about GEOMETRY… Properties of Polygons, Pythagorean Theorem Formulas for Polygons where n means the number of sides: • Exterior Angle Measurement of a Regular Polygon: 360÷n • Sum of Interior Angles: 180(n – 2) • Interior Angle Measurement of a regular polygon: • An interior angle and an exterior angle of a regular polygon always add up to 180° Interior angle Exterior angle Diagonals of a Polygon where n stands for the number of vertices (which is equal to the number of sides): • • A diagonal is a segment that connects one vertex of a polygon to another vertex that is not directly next to it. The dashed lines represent some of the diagonals of this pentagon. Pythagorean Theorem • a2 + b2 = c2 • a and b are the legs of the triangle and c is the hypotenuse (the side opposite the right angle) c a b • Common Right triangles are ones with sides 3, 4, 5, with sides 5, 12, 13, with sides 7, 24, 25, and multiples thereof—Memorize these! Category 2 50th anniversary edition Geometry 26 Y Meet #3 - January, 2014 W 1) How many cm long is segment 6 XY ? All measurements are in centimeters (cm). -

Seven Wonders Time: 30 Minutes Level: Beginner
Lesson Five: Seven Wonders Time: 30 minutes Level: Beginner Intro The Seven Wonders of the Ancient World were architectural feats recorded by ancient historians, writers and scholars in the western world - the list is limited geographically to the mediterranean, the centre of ancient western civilization. The only remaining wonder in the present day is the Great Pyramid of Giza, which is also the oldest. The rest have all been destroyed by weather, war or nature. Today we’re going to learn a little bit about each one: The Great Pyramid of Giza The pyramids are, in many ways, the most famous ancient wonder of the world. Whether that’s attributed to their mystery, incredible feat of construction, or their sole survival (out of all of the ancient wonders) into the modern era, all marvel at their magnificence. The Great Pyramid of Giza was constructed around 2589-2566 B.C. during the reign of Pharaoh Khufu. It stood about 147 meters tall and its base was approximately 230 meters in length. The second pyramid was created for Khufu’s son, Pharaoh Khafre, in 2558-2532 B.C. Within the pyramid’s complex at Giza was the largest statue in the world at that time, known as the Great Sphinx (a man’s head on a lion’s body), standing 240 feet long and 66 feet tall. The last pyramid was built around 2532-2503 B.C. for Khafre’s son, Pharaoh Menkaure. It was the shortest of the three pyramids in this ancient wonder, standing at only 216 feet tall. It took over 2.3 million blocks of limestone, 100,000 men, and 20 years to construct the greatest architectural achievement in the ancient world.