DOCSLIB.ORG

Year 6 – Wednesday 24Th June 2020 – Maths

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

1 Year 6 – Wednesday 24th June 2020 – Maths Can I identify 3D shapes that have pairs of parallel or perpendicular edges? Parallel – edges that have the same distance continuously between them – parallel edges never meet. Perpendicular – when two edges or faces meet and create a 90o angle. 1 4. 7. 10. 2 5. 8. 11. 3. 6. 9. 12. C1 – Using the shapes above: 1. Name and sort the shapes into: a. Pyramids b. Prisms 2. Draw a table to identify how many faces, edges and vertices each shape has. 3. Write your own geometric definition: a. Prism b. pyramid 4. Which shape is the odd one out? Explain why. C2 – Using the shapes above; 1. Which of the shapes have pairs of parallel edges in: a. All their faces? b. More than one half of the faces? c. One face only? 2. The following shapes have pairs of perpendicular edges. Identify the faces they are in: 2 a. A cube b. A square based pyramid c. A triangular prism d. A cuboid 3. Which shape with straight edges has no perpendicular edges? 4. Which shape has perpendicular edges in the shape but not in any face? C3 – Using the above shapes: 1. How many faces have pairs of parallel edges in: a. A hexagonal pyramid? b. A decagonal (10-sided) based prism? c. A heptagonal based prism? d. Which shape has no face with parallel edges but has parallel edges in the shape? 2. How many faces have perpendicular edges in: a. A pentagonal pyramid b. A hexagonal pyramid c. A heptagonal based prism d. A decagonal based prism 3. How many edges are there on the end faces of a prism with 9 faces with perpendicular edges? 3 Year 6 - Wednesday 24th June 2020 – Reading & Spelling Reading Task: Read the passage below and use the information to answer the comprehension questions. Answer the following the questions: 1. How many siblings does Hestia have and what are their names? 2. How does her personality differ from Poseidon and Zeus? 3. Why were new born children presented to hearths? 4. Why do you think cities had public fires that were never allowed to go out? Spelling Task: Focus: Spellings across the curriculum – Computing These are words which children will commonly use across the curriculum. Children should read, spell and pronounce vocabulary correctly (where appropriate). Challenge 1 Challenge 2 Challenge 3 hardware network keyboard software graphic megabyte server electronic spreadsheet output database multimedia Why not try using this website to help you learn your spellings: http://www.danitech.co.uk/buttsbury/spellings/ Task: Write each spelling out and then trace over it in 4 different colours. - Have you used cursive handwriting? - Check each spelling against the chart to ensure it is correct. 4 Year 6 - Wednesday 24th June 2020 – Literacy Can I describe a mythical creature? Task: Draw a Greek mythical creature and describe it. You can use one below or you can create your own. C1: Choose a mythical creature from the images below, draw it out and label its key features making it mythical (something we wouldn’t find in today’s world). C2: Choose any mythical creature, label the features that make it mythical and write a short description of its appearance. C3: Create your own mythical creature and write a description of what makes it mythical, its appearance and include comparisons to real world animals. Key features to include: Draw your chosen Greek mythical creature. Add its height and weight. Include powerful adjectives What strengths does you mythical creature possess? What part of Greece do they originate form? What two animals are they crossed between? 5 Year 6 Ancient Greeks – Wednesday 24th June 2020 Can I sort Olympic sports? The Greeks loved sport and the Olympic Games were the biggest sporting event in the ancient calendar. The Olympic Games began over 2,700 years ago in Olympia, in south west Greece. Every four years, around 50,000 people came from all over the Greek world to watch and take part. The ancient games were also a religious festival, held in honour of Zeus, the king of the gods. Use this clip to find out more. You can click on the pictures of the sports to learn more about them. https://www.bbc.co.uk/bitesize/topics/z87tn39/articles/z36j7ty Task: We would like you to sort the Sports below into a Venn diagram. If they are an ancient Greek sport they will go in the Ancient Greek section, if they are a modern sport, put them in the modern section. If they appeared in both Ancient and modern day Olympics, put them in the middle. Sports to sort: Running Jumping Gymnastics Boxing Swimming Cycling Pankration Wrestling Canoeing Volleyball Archery Chariot racing Discus Javelin throw Taekwondo Basketball 6 Year 6 Marking – Wednesday 24th June 2020 Maths Marking: C1 1. a. tetrahedron, square based pyramid, hexagonal pyramid b. cube, cuboid, triangular prism, pentagonal prism, hexagonal prism, heptagonal prism, octagonal prism, decagonal prism 2. Face Edges Vertices Tetrahedron 4 6 4 Pentagonal prism 7 15 10 Decagonal prism 12 30 20 Octahedron 8 12 6 Triangular prism 6 9 6 Heptagonal prism 9 21 14 Square based pyramid 5 8 5 Octagonal prism 10 24 16 Hexagonal pyramid 7 12 7 Cube 6 12 8 Hexagonal prism 8 18 12 Cuboid 6 12 8 3. 4. Octahedron – it doesn’t fit to the definition of a a. Prism - is a solid object with identical ends, flat prism as it does not have an equal cross section faces and the same cross section all along its length. throughout. It also isn’t a pyramid as it doesn’t have b. Pyramid - is made by connecting a base to a base. an apex C2 1. A – Cuboid, cube, hexagonal prism, octagonal prism B – pentagonal prism, triangular prism C – square based pyramid 2. A – All B – The base C – Rectangular faces D – All 3. Tetrahedron 4. Octahedron C3 1. 2. 3. A – 1 A – 0 7 on each end face B – 12 B – 0 C – 7 C – 7 D – Octahedron D – 10 Reading & Spelling Marking: 1. Five: Zeus, Poseidon, Hades, Hera and Demeter. 2. Hestia is calm and gentle whereas Zeus and Poseidon are seen as more bad-tempered. 3. New born children were presented to hearths to receive Hestia’s blessing. 7 4. Answers will vary but should include reference to Hestia’s blessing and keeping the town safe/protected. Literacy Marking: Subjective – Ensure all the points have been met from the Features to Include section. Your child can be as creative as they like with this task ensuring all labels and descriptions are met. Foundation Marking: Olympic Sorting Answers: • Running – Both • Jumping - Both • Gymnastics - Modern • Boxing - Both • Swimming - Modern • Cycling - Modern • Pankration - Ancient • Wrestling - Both • Canoeing - Modern • Volleyball - Modern • Archery - Modern • Chariot racing - Ancient • Discus - Both • Javelin throw - Modern • Taekwondo - Modern • Basketball - Modern .
Recommended publications
  • Volumes of Prisms and Cylinders 625

    Volumes of Prisms and Cylinders 625

    11-4 11-4 Volumes of Prisms and 11-4 Cylinders 1. Plan Objectives What You’ll Learn Check Skills You’ll Need GO for Help Lessons 1-9 and 10-1 1 To find the volume of a prism 2 To find the volume of • To find the volume of a Find the area of each figure. For answers that are not whole numbers, round to prism a cylinder the nearest tenth. • To find the volume of a 2 Examples cylinder 1. a square with side length 7 cm 49 cm 1 Finding Volume of a 2. a circle with diameter 15 in. 176.7 in.2 . And Why Rectangular Prism 3. a circle with radius 10 mm 314.2 mm2 2 Finding Volume of a To estimate the volume of a 4. a rectangle with length 3 ft and width 1 ft 3 ft2 Triangular Prism backpack, as in Example 4 2 3 Finding Volume of a Cylinder 5. a rectangle with base 14 in. and height 11 in. 154 in. 4 Finding Volume of a 6. a triangle with base 11 cm and height 5 cm 27.5 cm2 Composite Figure 7. an equilateral triangle that is 8 in. on each side 27.7 in.2 New Vocabulary • volume • composite space figure Math Background Integral calculus considers the area under a curve, which leads to computation of volumes of 1 Finding Volume of a Prism solids of revolution. Cavalieri’s Principle is a forerunner of ideas formalized by Newton and Leibniz in calculus. Hands-On Activity: Finding Volume Explore the volume of a prism with unit cubes.
  • Geometric Shapes and Cut Sections

    Geometric Shapes and Cut Sections

    GEOMETRIC SHAPES AND CUT SECTIONS MODEL NO: EG.GEO • Wooden and Perspex Material • Long Life and Sturdy • Solid and Hollow sections • Clear Labeling • Small and Large sizes • Magnetic Fractions also Available Object Drawing Models Interpenetration of Solids Models Dissected and Non-Dissected • Two Cylinders of Different Diameters Cube Penetrating Each Other at Right Angles Cone • Two Cylinders of Different Diameters with Sphere Oblique Penetration Cylinder • A Cylinder into a Cone with Oblique Rectangular Prism Penetration Rectangular Pyramid • A Cone & Cylinder with Penetration at Triangular Prism Right Angles Triangular Pyramid • Two Cones at Right Angles Square Prism • Two Square Prisms of Different Sizes at Square Pyramid Right Angles Pentagonal Prism • Two Square Prisms at Oblique Angles Pentagonal Pyramid • Sphere & Cone at Centre Hexagonal Prism • Sphere & Cylinder Eccentric Hexagonal Pyramid • Sphere &Cylinder at Centre Octagonal Prism Octagonal Pyramid Decagonal Prism Decagonal Pyramid Development of Surface for all Shapes *Oblique Polyhedrons for Above Available Available TEACHING AIDS FOR ENGINEERING DRAWING Set of Cut Sectioned Geometric Shapes Set of Solid Wooden Prism and Pyramids Set of Oblique Polyhedrons Set of Geometric Shapes with Development of Surface Paper Nets * Mechmatics reserves the right to modify its Product without notice * In the interest of continued improvements to our products, we reserve the right to change specifications without prior notification. Common Examples of Loci of Point with Pencil tracing position and Theoretical Diagrams * In the interest of continued improvements to our products, we reserve the right to change specifications without prior notification. DEVELOPMENT OF SURFACES MODEL ED.DS A development is the unfold / unrolled flat / plane figure of a 3-D object.
  • Math 366 Lecture Notes Section 11.4 – Geometry in Three Dimensions

    Math 366 Lecture Notes Section 11.4 – Geometry in Three Dimensions

    Section 11-4 Math 366 Lecture Notes Section 11.4 – Geometry in Three Dimensions Simple Closed Surfaces A simple closed surface has exactly one interior, no holes, and is hollow. A sphere is the set of all points at a given distance from a given point, the center . A sphere is a simple closed surface. A solid is a simple closed surface with all interior points. (see p. 726) A polyhedron is a simple closed surface made up of polygonal regions, or faces . The vertices of the polygonal regions are the vertices of the polyhedron, and the sides of each polygonal region are the edges of the polyhedron. (see p. 726-727) A prism is a polyhedron in which two congruent faces lie in parallel planes and the other faces are bounded by parallelograms. The parallel faces of a prism are the bases of the prism. A prism is usually names after its bases. The faces other than the bases are the lateral faces of a prism. A right prism is one in which the lateral faces are all bounded by rectangles. An oblique prism is one in which some of the lateral faces are not bounded by rectangles. To draw a prism: 1) Draw one of the bases. 2) Draw vertical segments of equal length from each vertex. 3) Connect the bottom endpoints to form the second base. Use dashed segments for edges that cannot be seen. A pyramid is a polyhedron determined by a polygon and a point not in the plane of the polygon. The pyramid consists of the triangular regions determined by the point and each pair of consecutive vertices of the polygon and the polygonal region determined by the polygon.
  • 10-4 Surface and Lateral Area of Prism and Cylinders.Pdf

    10-4 Surface and Lateral Area of Prism and Cylinders.Pdf

    Aim: How do we evaluate and solve problems involving surface area of prisms an cylinders? Objective: Learn and apply the formula for the surface area of a prism. Learn and apply the formula for the surface area of a cylinder. Vocabulary: lateral face, lateral edge, right prism, oblique prism, altitude, surface area, lateral surface, axis of a cylinder, right cylinder, oblique cylinder. Prisms and cylinders have 2 congruent parallel bases. A lateral face is not a base. The edges of the base are called base edges. A lateral edge is not an edge of a base. The lateral faces of a right prism are all rectangles. An oblique prism has at least one nonrectangular lateral face. An altitude of a prism or cylinder is a perpendicular segment joining the planes of the bases. The height of a three-dimensional figure is the length of an altitude. Surface area is the total area of all faces and curved surfaces of a three-dimensional figure. The lateral area of a prism is the sum of the areas of the lateral faces. Holt Geometry The net of a right prism can be drawn so that the lateral faces form a rectangle with the same height as the prism. The base of the rectangle is equal to the perimeter of the base of the prism. The surface area of a right rectangular prism with length ℓ, width w, and height h can be written as S = 2ℓw + 2wh + 2ℓh. The surface area formula is only true for right prisms. To find the surface area of an oblique prism, add the areas of the faces.
  • Unit 6 Visualising Solid Shapes(Final)

    Unit 6 Visualising Solid Shapes(Final)

    • 3D shapes/objects are those which do not lie completely in a plane. • 3D objects have different views from different positions. • A solid is a polyhedron if it is made up of only polygonal faces, the faces meet at edges which are line segments and the edges meet at a point called vertex. • Euler’s formula for any polyhedron is, F + V – E = 2 Where F stands for number of faces, V for number of vertices and E for number of edges. • Types of polyhedrons: (a) Convex polyhedron A convex polyhedron is one in which all faces make it convex. e.g. (1) (2) (3) (4) 12/04/18 (1) and (2) are convex polyhedrons whereas (3) and (4) are non convex polyhedron. (b) Regular polyhedra or platonic solids: A polyhedron is regular if its faces are congruent regular polygons and the same number of faces meet at each vertex. For example, a cube is a platonic solid because all six of its faces are congruent squares. There are five such solids– tetrahedron, cube, octahedron, dodecahedron and icosahedron. e.g. • A prism is a polyhedron whose bottom and top faces (known as bases) are congruent polygons and faces known as lateral faces are parallelograms (when the side faces are rectangles, the shape is known as right prism). • A pyramid is a polyhedron whose base is a polygon and lateral faces are triangles. • A map depicts the location of a particular object/place in relation to other objects/places. The front, top and side of a figure are shown. Use centimetre cubes to build the figure.
  • Triangulation of Simple 3D Shapes with Well-Centered Tetrahedra

    Triangulation of Simple 3D Shapes with Well-Centered Tetrahedra

    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Illinois Digital Environment for Access to Learning and Scholarship Repository TRIANGULATION OF SIMPLE 3D SHAPES WITH WELL-CENTERED TETRAHEDRA EVAN VANDERZEE, ANIL N. HIRANI, AND DAMRONG GUOY Abstract. A completely well-centered tetrahedral mesh is a triangulation of a three dimensional domain in which every tetrahedron and every triangle contains its circumcenter in its interior. Such meshes have applications in scientific computing and other fields. We show how to triangulate simple domains using completely well-centered tetrahedra. The domains we consider here are space, infinite slab, infinite rectangular prism, cube, and regular tetrahedron. We also demonstrate single tetrahedra with various combinations of the properties of dihedral acuteness, 2-well-centeredness, and 3-well-centeredness. 1. Introduction 3 In this paper we demonstrate well-centered triangulation of simple domains in R . A well- centered simplex is one for which the circumcenter lies in the interior of the simplex [8]. This definition is further refined to that of a k-well-centered simplex which is one whose k-dimensional faces have the well-centeredness property. An n-dimensional simplex which is k-well-centered for all 1 ≤ k ≤ n is called completely well-centered [15]. These properties extend to simplicial complexes, i.e. to meshes. Thus a mesh can be completely well-centered or k-well-centered if all its simplices have that property. For triangles, being well-centered is the same as being acute-angled. But a tetrahedron can be dihedral acute without being 3-well-centered as we show by example in Sect.
  • Uniform Panoploid Tetracombs

    Uniform Panoploid Tetracombs

    Uniform Panoploid Tetracombs George Olshevsky TETRACOMB is a four-dimensional tessellation. In any tessellation, the honeycells, which are the n-dimensional polytopes that tessellate the space, Amust by definition adjoin precisely along their facets, that is, their ( n!1)- dimensional elements, so that each facet belongs to exactly two honeycells. In the case of tetracombs, the honeycells are four-dimensional polytopes, or polychora, and their facets are polyhedra. For a tessellation to be uniform, the honeycells must all be uniform polytopes, and the vertices must be transitive on the symmetry group of the tessellation. Loosely speaking, therefore, the vertices must be “surrounded all alike” by the honeycells that meet there. If a tessellation is such that every point of its space not on a boundary between honeycells lies in the interior of exactly one honeycell, then it is panoploid. If one or more points of the space not on a boundary between honeycells lie inside more than one honeycell, the tessellation is polyploid. Tessellations may also be constructed that have “holes,” that is, regions that lie inside none of the honeycells; such tessellations are called holeycombs. It is possible for a polyploid tessellation to also be a holeycomb, but not for a panoploid tessellation, which must fill the entire space exactly once. Polyploid tessellations are also called starcombs or star-tessellations. Holeycombs usually arise when (n!1)-dimensional tessellations are themselves permitted to be honeycells; these take up the otherwise free facets that bound the “holes,” so that all the facets continue to belong to two honeycells. In this essay, as per its title, we are concerned with just the uniform panoploid tetracombs.
  • 2D and 3D Shapes.Pdf

    2D and 3D Shapes.Pdf

    & • Anchor 2 - D Charts • Flash Cards 3 - D • Shape Books • Practice Pages rd Shapesfor 3 Grade by Carrie Lutz T hank you for purchasing!!! Check out my store: http://www.teacherspayteachers.com/Store/Carrie-Lutz-6 Follow me for notifications of freebies, sales and new arrivals! Visit my BLOG for more Free Stuff! Read My Blog Post about Teaching 3 Dimensional Figures Correctly Credits: Carrie Lutz©2016 2D Shape Bank 3D Shape Bank 3 Sided 5 Sided Prisms triangular prism cube rectangular prism triangle pentagon 4 Sided rectangle square pentagonal prism hexagonal prism octagonal prism Pyramids rhombus trapezoid 6 Sided 8 Sided rectangular square triangular pyramid pyramid pyramid Carrie LutzCarrie CarrieLutz pentagonal hexagonal © hexagon octagon © 2016 pyramid pyramid 2016 Curved Shapes CURVED SOLIDS oval circle sphere cone cylinder Carrie Lutz©2016 Carrie Lutz©2016 Name _____________________ Side Sort Date _____________________ Cut out the shapes below and glue them in the correct column. More than 4 Less than 4 Exactly 4 Carrie Lutz©2016 Name _____________________ Name the Shapes Date _____________________ 1. Name the Shape. 2. Name the Shape. 3. Name the Shape. ____________________________________ ____________________________________ ____________________________________ 4. Name the Shape. 5. Name the Shape. 6. Name the Shape. ____________________________________ ____________________________________ ____________________________________ 4. Name the Shape. 5. Name the Shape. 6. Name the Shape. ____________________________________ ____________________________________ ____________________________________ octagon circle square rhombus triangle hexagon pentagon rectangle trapezoid Carrie Lutz©2016 Faces, Edges, Vertices Name _____________________ and Date _____________________ 1. Name the Shape. 2. Name the Shape. 3. Name the Shape. ____________________________________ ____________________________________ ____________________________________ _____ faces _____ faces _____ faces _____Edges _____Edges _____Edges _____Vertices _____Vertices _____Vertices 4.
  • Lesson 23: the Volume of a Right Prism

    Lesson 23: the Volume of a Right Prism

    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 23 7•3 Lesson 23: The Volume of a Right Prism Student Outcomes . Students use the known formula for the volume of a right rectangular prism (length × width × height). Students understand the volume of a right prism to be the area of the base times the height. Students compute volumes of right prisms involving fractional values for length. Lesson Notes Students extend their knowledge of obtaining volumes of right rectangular prisms via dimensional measurements to understand how to calculate the volumes of other right prisms. This concept will later be extended to finding the volumes of liquids in right prism-shaped containers and extended again (in Module 6) to finding the volumes of irregular solids using displacement of liquids in containers. The Problem Set scaffolds in the use of equations to calculate unknown dimensions. Classwork Opening Exercise (5 minutes) Opening Exercise The volume of a solid is a quantity given by the number of unit cubes needed to fill the solid. Most solids—rocks, baseballs, people—cannot be filled with unit cubes or assembled from cubes. Yet such solids still have volume. Fortunately, we do not need to assemble solids from unit cubes in order to calculate their volume. One of the first interesting examples of a solid that cannot be assembled from cubes, but whose volume can still be calculated from a formula, is a right triangular prism. What is the area of the square pictured on the right? Explain. The area of the square is ퟑퟔ 퐮퐧퐢퐭퐬ퟐ because the region is filled with ퟑퟔ square regions that are ퟏ 퐮퐧퐢퐭 by ퟏ 퐮퐧퐢퐭, or ퟏ 퐮퐧퐢퐭ퟐ.
  • [ENTRY POLYHEDRA] Authors: Oliver Knill: December 2000 Source: Translated Into This Format from Data Given In

    [ENTRY POLYHEDRA] Authors: Oliver Knill: December 2000 Source: Translated Into This Format from Data Given In

    ENTRY POLYHEDRA [ENTRY POLYHEDRA] Authors: Oliver Knill: December 2000 Source: Translated into this format from data given in http://netlib.bell-labs.com/netlib tetrahedron The [tetrahedron] is a polyhedron with 4 vertices and 4 faces. The dual polyhedron is called tetrahedron. cube The [cube] is a polyhedron with 8 vertices and 6 faces. The dual polyhedron is called octahedron. hexahedron The [hexahedron] is a polyhedron with 8 vertices and 6 faces. The dual polyhedron is called octahedron. octahedron The [octahedron] is a polyhedron with 6 vertices and 8 faces. The dual polyhedron is called cube. dodecahedron The [dodecahedron] is a polyhedron with 20 vertices and 12 faces. The dual polyhedron is called icosahedron. icosahedron The [icosahedron] is a polyhedron with 12 vertices and 20 faces. The dual polyhedron is called dodecahedron. small stellated dodecahedron The [small stellated dodecahedron] is a polyhedron with 12 vertices and 12 faces. The dual polyhedron is called great dodecahedron. great dodecahedron The [great dodecahedron] is a polyhedron with 12 vertices and 12 faces. The dual polyhedron is called small stellated dodecahedron. great stellated dodecahedron The [great stellated dodecahedron] is a polyhedron with 20 vertices and 12 faces. The dual polyhedron is called great icosahedron. great icosahedron The [great icosahedron] is a polyhedron with 12 vertices and 20 faces. The dual polyhedron is called great stellated dodecahedron. truncated tetrahedron The [truncated tetrahedron] is a polyhedron with 12 vertices and 8 faces. The dual polyhedron is called triakis tetrahedron. cuboctahedron The [cuboctahedron] is a polyhedron with 12 vertices and 14 faces. The dual polyhedron is called rhombic dodecahedron.
  • Understanding by Design Unit Template

    Understanding by Design Unit Template

    WEST SHORE SCHOOL DISTRICT Math Learning Module 5 Title of Module Module 5: Addition and Multiplication with Grade Level 5th Grade Volume and Area Curriculum Area Math Time Frame enVision Math Topic 10, Topic 15 (MP 3) Best Practices MP# 1. Make sense of problems and persevere in solving them MP# 2. Reason abstractly and quantitatively MP# 4. Model with mathematics MP# 3. Construct viable arguments and critique the reasoning of others MP# 5. Use appropriate tools strategically MP# 6. Attend to precision MP# 7. Look for and make use of structure (Deductive Reasoning) MP# 8. Look for and express regularity in repeated reasoning Transfer Goals 1. Interpret and persevere in solving complex mathematical problems using strategic thinking and expressing answers with a degree of precision appropriate for the problem context. 2. Express appropriate mathematical reasoning by constructing viable arguments, critiquing the reasoning of others, and attending to precision when making mathematical statements. 3. Apply mathematical knowledge to analyze and model mathematical relationships in the context of a situation in order to make decisions, draw conclusions, and solve problems. Key Learnings/Big Ideas Through the daily use of area models, the fraction module prepares students for an in-depth discussion of area and volume in Module 5. But the module on area and volume also reinforces work done in the fraction module: Now, questions about how the area changes when a rectangle is scaled by a whole or fractional scale factor may be asked. Measuring volume once again highlights the unit theme, as a unit cube is chosen to represent a volume unit and used to measure the volume of simple shapes composed out of rectangular prisms.
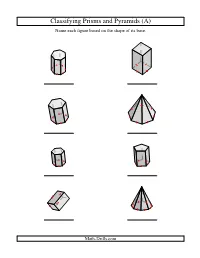
  • Geometry Worksheet -- Classifying Prisms and Pyramids

    Geometry Worksheet -- Classifying Prisms and Pyramids

    Classifying Prisms and Pyramids (A) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (A) Answers Name each figure based on the shape of its base. heptagonal prism square prism hexagonal prism heptagonal pyramid hexagonal prism pentagonal prism rectangular prism octagonal pyramid Math-Drills.com Classifying Prisms and Pyramids (B) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (B) Answers Name each figure based on the shape of its base. square prism heptagonal pyramid pentagonal pyramid triangular prism square pyramid rectangular prism triangular prism rectangular pyramid Math-Drills.com Classifying Prisms and Pyramids (C) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (C) Answers Name each figure based on the shape of its base. pentagonal pyramid square prism, cube octagonal prism heptagonal pyramid heptagonal pyramid rectangular pyramid rectangular prism pentagonal prism Math-Drills.com Classifying Prisms and Pyramids (D) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (D) Answers Name each figure based on the shape of its base. square pyramid heptagonal prism hexagonal prism heptagonal pyramid square prism, cube square pyramid triangular prism octagonal prism Math-Drills.com Classifying Prisms and Pyramids (E) Name each figure based on the shape of its base. Math-Drills.com Classifying Prisms and Pyramids (E) Answers Name each figure based on the shape of its base. square prism octagonal prism rectangular prism octagonal prism pentagonal pyramid hexagonal prism pentagonal prism heptagonal pyramid Math-Drills.com Classifying Prisms and Pyramids (F) Name each figure based on the shape of its base.