COMP6053 Lecture: Principal Components Analysis
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Women's 3000M Steeplechase
Games of the XXXII Olympiad • Biographical Entry List • Women Women’s 3000m Steeplechase Entrants: 47 Event starts: August 1 Age (Days) Born SB PB 1003 GEGA Luiza ALB 32y 266d 1988 9:29.93 9:19.93 -19 NR Holder of all Albanian records from 800m to Marathon, plus the Steeplechase 5000 pb: 15:36.62 -19 (15:54.24 -21). 800 pb: 2:01.31 -14. 1500 pb: 4:02.63 -15. 3000 pb: 8:52.53i -17, 8:53.78 -16. 10,000 pb: 32:16.25 -21. Half Mar pb: 73:11 -17; Marathon pb: 2:35:34 -20 ht EIC 800 2011/2013; 1 Balkan 1500 2011/1500; 1 Balkan indoor 1500 2012/2013/2014/2016 & 3000 2018/2020; ht ECH 800/1500 2012; 2 WSG 1500 2013; sf WCH 1500 2013 (2015-ht); 6 WIC 1500 2014 (2016/2018-ht); 2 ECH 3000SC 2016 (2018-4); ht OLY 3000SC 2016; 5 EIC 1500 2017; 9 WCH 3000SC 2019. Coach-Taulant Stermasi Marathon (1): 1 Skopje 2020 In 2021: 1 Albanian winter 3000; 1 Albanian Cup 3000SC; 1 Albanian 3000/5000; 11 Doha Diamond 3000SC; 6 ECP 10,000; 1 ETCh 3rd League 3000SC; She was the Albanian flagbearer at the opening ceremony in Tokyo (along with weightlifter Briken Calja) 1025 CASETTA Belén ARG 26y 307d 1994 9:45.79 9:25.99 -17 Full name-Belén Adaluz Casetta South American record holder. 2017 World Championship finalist 5000 pb: 16:23.61 -16. 1500 pb: 4:19.21 -17. 10 World Youth 2011; ht WJC 2012; 1 Ibero-American 2016; ht OLY 2016; 1 South American 2017 (2013-6, 2015-3, 2019-2, 2021-3); 2 South American 5000 2017; 11 WCH 2017 (2019-ht); 3 WSG 2019 (2017-6); 3 Pan-Am Games 2019. -

Media Kit Contents
2005 IAAF World Outdoor Track & Field Championship in Athletics August 6-14, 2005, Helsinki, Finland Saturday, August 06, 2005 Monday, August 08, 2005 Morning session Afternoon session Time Event Round Time Event Round Status 10:05 W Triple Jump QUALIFICATION 18:40 M Hammer FINAL 10:10 W 100m Hurdles HEPTATHLON 18:50 W 100m SEMI-FINAL 10:15 M Shot Put QUALIFICATION 19:10 W High Jump FINAL 10:45 M 100m HEATS 19:20 M 10,000m FINAL 11:15 M Hammer QUALIFICATION A 20:05 M 1500m SEMI-FINAL 11:20 W High Jump HEPTATHLON 20:35 W 3000m Steeplechase FINAL 12:05 W 3000m Steeplechase HEATS 21:00 W 400m SEMI-FINAL 12:45 W 800m HEATS 21:35 W 100m FINAL 12:45 M Hammer QUALIFICATION B Tuesday, August 09, 2005 13:35 M 400m Hurdles HEATS Morning session 13:55 W Shot Put HEPTATHLON 11:35 M 100m DECATHLON\ Afternoon session 11:45 M Javelin QUALIFICATION A 18:35 M Discus QUALIFICATION A 12:10 M Pole Vault QUALIFICATION 18:40 M 20km Race Walking FINAL 12:20 M 200m HEATS 18:45 M 100m QUARTER-FINAL 12:40 M Long Jump DECATHLON 19:25 W 200m HEPTATHLON 13:20 M Javelin QUALIFICATION B 19:30 W High Jump QUALIFICATION 13:40 M 400m HEATS 20:05 M Discus QUALIFICATION B Afternoon session 20:30 M 1500m HEATS 14:15 W Long Jump QUALIFICATION 20:55 M Shot Put FINAL 14:25 M Shot Put DECATHLON 21:15 W 10,000m FINAL 17:30 M High Jump DECATHLON 18:35 W Discus FINAL Sunday, August 07, 2005 18:40 W 100m Hurdles HEATS Morning session 19:25 M 200m QUARTER-FINAL 11:35 W 20km Race Walking FINAL 20:00 M 3000m Steeplechase FINAL 11:45 W Discus QUALIFICATION 20:15 M Triple Jump QUALIFICATION -

Tokyo 2020 Olympic Games Nomination Criteria
Tokyo 2020 Olympic Games Nomination Criteria Selection Criteria Amendments • February 19, 2021 o Section 1.2: . Removed reference to NACAC Combined Events Championships, which has been cancelled. The dates and location of the Canadian Combined Events Trials is now to-be-confirmed. Moved the Final Nomination for Marathon and Race Walk to July 2 to align with all other events. Moved the final declaration deadline for all events to June 10, 2021. Updated dates for: Final Preparation Camp, On-site Decision Making Authority, Athletics Competition and Departing Japan o Section 1.3: . Removed requirement to participate in Canadian Championships. Added requirement to comply with COVID-19 countermeasures. o Section 1.6: Added reference to Reserve Athletes. o Section 3: Removed requirement to participate in Canadian Championships. o Section 4.1 . Step 2: Removed: “For the avoidance of doubt, the NTC will not nominate athletes for individual events who are only qualified to be entered due to World Athletics’ “reallocations due to unused quota places” after July 1, 2021 (June 2, 2021 for Marathon and Race Walk).” . Final Nomination Meeting: Added prioritization process for athletes qualifying for both the Women’s Marathon and 10,000m. o Section 4.2: . Removed: “AC will not accept any offers of unused quota places for relay teams made after July 1, 2021;” . Step 1: Removed automatic nomination for national champions. o Section 8: Added language regarding possible further amendments necessitated by COVID-19. • October 6, 2020 o Section 1.2: Updated qualification period to match World Athletics adjustments for Marathon and 50k Race Walk. Updated dates for NACAC Combined Events Championships (Athletics Canada Combined Events Trials). -

European Athletics U20 Championships • Biographical Entrylist, Women
100m European Athletics U20 Championships • Biographical Entrylist, Women Age (Days) Year SB PB HUNT Amy GBR 19y 60d 2002 11.31 -19 200m European U20 Champion 2019 / 4 x 100m European U20 Champion 2019 / 1 National Title (60 indoors 2020) 100m pb 11.31 Loughborough -19 150S 17.31 Gateshead -17 200 22.42 WU18B Mannheim -19 1 EJ 200 2019 (1 4x1) England. Club: Charnwood. Coach-Joseph McDonnell. Runs in New Balance shoes. In 2021: 2 Birmingham 200 (23.73); 3 -19 Bedford NC-j 200 (23.92) ADELEKE Rhasidat IRL 18y 319d 2002 11.31 11.31 -21 2 National Titles (100 outdoors 2021) (200 indoors 2019) 100m pb 11.31 NU23R Manhattan KS -21 200 22.96 NR NU23R Manhattan KS -21 LJ 5.39 Tullamore -16 h WJC 4x1 2018 Club: Tallaght. Studies at University of Texas. Coach-Edrick Floréal, CAN (long jump pb 8.20 NR in 1991, triple jump pb 17.29 in 1989)/Daniel Kilgallon. From Dublin. In 2021: 4 Fayetteville AR 200 ind; 8 College Station TX 60 ind; 1 Fayetteville AR 400 ind; 3 rB Lubbock TX Big 12 400 ind (53.44 pb); 6 Austin TX TexasR 200; 3 Austin TX 200; 5 Baton Rouge LA 200; 2 Austin TX 200; 1 Austin TX 100; 2 Manhattan KS Big 12 100; 2 Manhattan KS Big 12 200 (23.03 NU23R); 1 Dublin NC 100 (11.29w pb); 2 Dublin NC 200 (22.84w pb) SEEDO N'ketia NED 18y 37d 2003 11.50 11.37 -19 100m European U20 Silver 2019 / 4 x 100m European U20 Silver 2019 / 1 National Title (60 indoors 2020) 100m pb 11.37 Borås -19 150 18.49 Utrecht -17 200 23.93 Alphen aan den Rijn -19 2 EJ 100 2019 (2 4x1) Club: U-Track. -
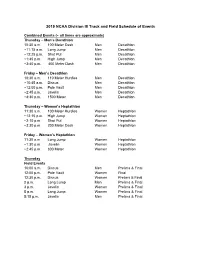
2019 NCAA Division III Track and Field Schedule of Events
2019 NCAA Division III Track and Field Schedule of Events Combined Events (~ all times are approximate) Thursday – Men’s Decathlon 10:30 a.m. 100 Meter Dash Men Decathlon ~11:15 a.m. Long Jump Men Decathlon ~12:25 p.m. Shot Put Men Decathlon ~1:45 p.m. High Jump Men Decathlon ~3:40 p.m. 400 Meter Dash Men Decathlon Friday – Men’s Decathlon 10:30 a.m. 110 Meter Hurdles Men Decathlon ~10:45 a.m. Discus Men Decathlon ~12:00 p.m. Pole Vault Men Decathlon ~2:45 p.m. Javelin Men Decathlon ~4:30 p.m. 1500 Meter Men Decathlon Thursday – Women’s Heptathlon 11:30 a.m. 100 Meter Hurdles Women Heptathlon ~12:15 p.m. High Jump Women Heptathlon ~2:10 p.m. Shot Put Women Heptathlon ~3:30 p.m. 200 Meter Dash Women Heptathlon Friday – Women’s Heptathlon 11:30 a.m. Long Jump Women Heptathlon ~1:30 p.m. Javelin Women Heptathlon ~2:45 p.m. 800 Meter Women Heptathlon Thursday Field Events 10:00 a.m. Discus Men Prelims & Final 12:00 p.m. Pole Vault Women Final 12:30 p.m. Discus Women Prelims & Final 2 p.m. Long Lump Men Prelims & Final 3 p.m. Javelin Women Prelims & Final 5 p.m. Long Jump Women Prelims & Final 5:15 p.m. Javelin Men Prelims & Final Thursday Track Events 9:45 a.m. 10000 Meter Women Final 10:45 a.m. 10000 Meter Men Final 2:50 p.m. National Anthem 3 p.m. 4x100 Meter Relay Men Prelims 3:15 p.m. -

2021 Decathlon Heptathlon Information
THE 64th NH STATE DECATHLON CHAMPIONSHIPS THE 44th NH STATE HEPTATHLON CHAMPIONSHIPS PRESENTED BY NASHUA SOUTH AT NASHUA HIGH SCHOOL NORTH June 18-20, 2021 MEET INFORMATION ENTRIES FOR HEPTATHLON AND DECATHLON ARE TO BE MADE ON DIRECT ATHLETICS FROM MAY 21st – JUNE 16th. PLEASE BE SURE TO INDICATE EACH ATHLETE’S PERSONAL BEST HIGH JUMP HEIGHT IN THE HEPTATHLON AND PERSONAL BEST POLE VAULT HEIGHT IN THE DECATHLON. THERE IS A $40 ENTRY FEE FOR EACH ATHLETE ENTERED. ENTRY FEES MUST BE PAID FOR ALL ATHLETES ENTERED IN ORDER FOR ANY OF YOUR ATHLETES TO COMPETE. IF YOU ENTERED AN ATHLETE THAT IS NOT COMPETING YOU MUST STILL PAY THE $40 ENTRY FEE. PLEASE REMOVE YOUR ATHLETE PRIOR TO THE 16th. YOUR SCHOOL WILL NOT BE ABLE TO PARTICIPATE IN FUTURE COMPETITIONS WITH AN UNPAID BALANCE. FEE MUST BE PAID BY OR ON FRIDAY, JUNE 18th OR SATURDAY, JUNE 19th, WHEN YOU ARRIVE. MAKE CHECKS PAYABLE TO: NASHUA HIGH SOUTH TRACK AND FIELD TEAM, C/O JASON PALING, 17 MEADE ST., NASHUA, NH 03064. **COMPETITION IS OPEN TO ALL HIGH SCHOOL ATHLETES, INCLUDING INCOMING (2021) FRESHMEN.** COMPETITORS IN DECATHLON AND HEPTATHLON ARE GROUPED SCHOOL, SCHOOL DISTRICT, THEN REGION. SCORING IS BASED ON THE INTERNATIONAL AMATEUR ATHLETIC FEDERATION SCORING TABLES FOR TRACK AND FIELD EVENTS. ALL ATHLETES MUST COMPLETE IN ALL EVENTS FOR ANY POINTS TO BE SCORED OR RECORDS TO BE MADE. ALL RUNNING EVENTS ARE BASED ON TIME. IN THE FIELD EVENTS, A MAXIMUM OF THREE THROWS/JUMPS WILL BE GIVEN. THERE WILL BE NO CONCESSIONS THIS YEAR. -

Heptathlon Evaluation Model Using Grey System Theory
CORE Metadata, citation and similar papers at core.ac.uk N. Slavek, A. Jović Model vrednovanja sedmoboja upotrebom sive relacijske analize ISSN 1330-3651 UDC/UDK 796.42.093.61.092.29:519.87 HEPTATHLON EVALUATION MODEL USING GREY SYSTEM THEORY Ninoslav Slavek, Alan Jović Original scientific paper In this paper we investigate the effectiveness of the Grey system theory to determine the ranking of the best women athletes in heptathlon. The scoring method currently used in women's heptathlon needs alternative scoring as it displays unacceptable bias towards some athletic disciplines while deferring others. The term Grey stands for poor, incomplete and uncertain, and is especially related to the information about the system. The Grey relational grade deduced by the Grey theory is used to establish a complete and accurate model for determining the ranking of the heptathletes. The proposed scoring method is accurate and is shown to improve fairness and results' validity in women's heptathlon. Keywords: Grey system theory, Grey relational analysis, heptathlon, ranking of heptathletes Model vrednovanja sedmoboja upotrebom sive relacijske analize Izvorni znanstveni članak U ovom radu istražujemo djelotvornost teorije Sivih sustava za utvrđivanje redoslijeda najboljih atletičarki u sedmoboju. Postojeća metoda bodovanja u ženskom sedmoboju treba alternativni način bodovanja jer pokazuje neprihvatljivu pristranost prema nekim atletskim disciplinama dok druge zanemaruje. Izraz Siviznači nešto siromašno, nepotpuno i neizvjesno, i posebno se odnosi na informaciju o sustavu. Sivi relacijski stupanj dobiven Sivom teorijom koristi se za uspostavu cjelokupnog itočnog modela za utvrđivanje redoslijeda sedmoboj ki. Predložena metoda bodovanja je točna i pokazano poboljšava pravednost i ispravnost rezultata ženskog sedmoboja. -

2021 Aau Junior Olympic Games Multi-Events/Racewalk
FINAL SCHEDULE- 7/25/21 2021 AAU JUNIOR OLYMPIC GAMES HUMBLE HIGH SCHOOL, HUMBLE, TEXAS MULTI-EVENT/TRACK & FIELD MEET SCHEDULE YOU ARE HEREBY NOTIFIED THAT THE MEET SCHEDULE OUTLINED BELOW IS SUBJECT TO CHANGE WITHOUT PRIOR WRITTEN NOTICE. CLASSIFICATION 8&UG - 8 and under (2013 & After) 12B - 12 years old (2009) 8&UB - 8 and under (2013 & After) 13G – 13 years old (2008) 9G - 9 years old (2012) 13B – 13 years old (2008) 9B - 9 years old (2012) 14G - 14 years old (2007) 10G - 10 years old (2011) 14B - 14 years old (2007) 10B - 10 years old (2011) 15-16G - 15-16 years old (2005-2006) 11G - 11 years old (2010) 15-16B - 15-16 years old (2005-2006) 11B - 11 years old (2010) 17-18G - 17-18 years old (2003-2004) 12G - 12 years old (2009) 17-18B- 17-18 years old (2003-2004) Q = Quarterfinals S = Semifinals F = Finals TF = Timed Final MULTI-EVENTS/RACEWALK SATURDAY, JULY 31 TIME EVENT/AGE GROUP RACE 8:00 AM Decathlon 15-16B (Day 1) 100M, LJ, SP, HJ, 400M 8:15 AM Pentathlon 13G (Finals) 100M Hurdles SP, HJ, LJ, 800M 8:30 AM Pentathlon 13B (Finals) 100M Hurdles, SP, HJ, LJ, 1500M 9:00 AM Decathlon 17-18B (Day 1) 100M, LJ, SP, HJ, 400M 10:30 AM Heptathlon 15-16G (Day 1) 100M Hurdles, HJ, SP, 200M 10:45 AM Heptathlon 17-18G (Day 1) 100M Hurdles, HJ, SP, 200M 11:00 AM Pentathlon 14G (Finals) 100M Hurdles, SP, HJ, LJ, 800M 11:30 AM Pentathlon 14B (Finals) 100M Hurdles, SP, HJ, LJ, 1500M 12:00 PM 1500M Racewalk (9G, 9B, 10G, 10B) TF 2:00 PM 1500M Racewalk (11G, 11B, 12G, 12B) TF SUNDAY, AUGUST 1 TIME EVENT/AGE GROUP RACE 8:00 AM Heptathlon 15-16G (Day -

FITNESS HEPTATHLON Season Runs from March 15Th – May 25Th
FITNESS HEPTATHLON Season runs from March 15th – May 25th WHAT IS THE FITNESS HEPTATHLON? The Fitness Heptathlon provides Special Olympics Pennsylvania (SOPA) participants with an opportunity to train and compete in an event comprised of 7 different fitness exercises. There are a wide range of offerings suited to meet the needs and interests of each individual. For competition, participants earn points based upon their performance improvement level in each exercise. EVENTS OFFERED: Athletes/Partners may choose from 1 of the following events: • Single (1 athlete) • Team (4 - 10 athletes) • Pairs (2 athletes) • Unified Teams (4-10 team members - 2 athletes & • Unified Pairs (1 athlete & 1 partner) 2 partners up to 5 athletes and 5 partners) REGISTRATION: Participants in the Fitness Heptathlon compete in seven exercise events. They will choose two (2) exercises from each of the following fitness area components, plus one (1) additional exercise from the full list, to make seven: AGILITY STRENGTH ENDURANCE 10 yd. Run, Walk, Roll* Squats Step Test 5-10-5 Run, Walk, Roll* Sit and Stand Jumping Jacks Box Agility * Wall Sits Burpee One Leg Stance - Eyes Open Standing Long Jump Jump Rope One Leg Stance - Eyes Closed Planks Mountain Climbers Seated Lateral Bends* Side to Side Jumps Power Punches* Ball Taps Curl Ups Front to Back Jumps Lane Slides Chair Push Ups* Seated Jumping Jacks* Push Ups Roman Holds* • Participants in Unified/Traditional pairs and teams are not required to do the same 7 exercises. • Asterisks* indicate exercises for participants in a wheel chair. PARTICIPANT REQUIREMENTS: • All Coaches or Unified Partners must be Class A volunteers • All individuals participating in in-person activities need to have an active medical. -

National Champions Men Denny Ellis 1965 Javelin Gary Berentsen 1966
National Champions Men Denny Ellis 1965 Javelin Gary Berentsen 1966 Javelin Dale Grant 1977 Javelin Kelly Jensen 1978 Steeplechase Randy Settell 1988 Shot Put Elliott Osborn 1993 Discus Paul Steenkolk 1998 Shot Put Robbie Johnston 2005 Pole Vault Scott Myers 2005 Shot Put Ryan Musselman 2008 Pole Vault Women Melanie Byrne 1988 Heptathlon Melaine Byrne 1988 Heptathlon Kris Ettner 1989 Javelin Theresa Walton 1994 Marathon Jill Carrier 1995 Heptathlon MEN’S ALL-AMERICAN Kevin Jeffers Steeple 6th 9:15.81 YEAR PERFORMER EVENT FINISH/MARK Trevor Palmer 1,500 6th 3:49.33 1965 Gary Berentsen Javelin 3rd 206-11 2008 Ryan Musselman* Pole Vault 1st 15-11 Denny Ellis* Javelin 1st 216-2 2009 Antwun Baker 100 6th 10.77 1966 Gary Berentsen* Javelin 1st 231-7 Cameron Kreuz 1,500 4th 3:47.83 Denny Ellis Javelin n/a n/a 2010 Alex Waroff Decathlon 6th 6,620 1969 Jamie Dixon Triple Jump 2nd 51-11 1/4 * NAIA Champion Harland Yriarte Discus 3rd 163-4 1970 Paul Osmond Hammer 5th 152-10 WOMEN’S ALL-AMERICAN Harland Yriarte Discus 4th 172-5 YEAR PERFORMER EVENT FINISH/MARK 1971 Paul Osmond Hammer 2nd n/a 1987 Elaine Delsman Marathon 3rd 3:02:00 Harland Yriarte Discus 2nd 167-6 Shannon Gates Javelin 2nd 156-10 1972 Larry Miller Marathon 3rd 2:43 1988 Melanie Byrne* Heptathlon 1st 4,812 1977 Dale Grant* Javelin 1st 236-11 1/2 Virginia Falkowski Marathon 2nd 3:03:48 1978 Kelly Jensen* Steeplechase 1st 8:47.49 1989 Melanie Byrne* Heptathlon 1st 5,132 1982 Terry Hendrix 200 — 21.3 Melanie Byrne High Jump 6th 5-7 1/4 1986 Ivan Parker Shot Put 5th 55-8 Kris Ettner* Javelin -

51034 Track and Field.Pdf
TRACK & FIELD CORPORATE PARTNERS TRACK & FIELD Track Coaches’ Committee (Listed By Districts) (1) Pat Galle, UMS-Wright [email protected]; Bi-District-Eddie Brun- didge, T.R. Miller [email protected]. (2) Chris Cooper, Dothan [email protected]. al.us. (3) Michael Floyd, Montgomery Academy michael_ floyd@ montgomeryacade- my.org; Bi-District-Angelo Wheeler, Park Crossing. (4) Glenn Copeland, Beauregard [email protected]. (5) Devon Hind, Hoover [email protected]; (5) Bi-District – Gary Ferguson, Shades Valley gfergu- [email protected]. (6) Mason Dye, St. Clair Co. [email protected]. (7) Nick Vinson, R.A. Hubbard [email protected]; Bi-District- Steve Reaves, Win- field. (8) Jace Wilemon, Falkville [email protected] The Championship Program First Practice—Feb. 9 First Contest—Mar. 1 Online Requirements For All Sports POSTING SCHEDULES Schools must post season schedules on the AHSAA website in the Members’ Area by the deadline dates listed below. Failure to do so could result in a fine assessed to the school. Schools may go online and make any changes immediately as they occur. Deadlines for posting schedules: April 1 — fall sports (football only) June 2 — fall sports (cross country, swimming & diving, volleyball, ) Sept. 16 — winter sports (basketball, bowling, indoor track, wrestling) Jan. 15 — spring sports (baseball, golf, outdoor track, soccer, softball, tennis) POSTING ROSTERS Schools are required to post team rosters prior to its first contest of the season. POSTING SCORES Schools are also required to post scores of contests online immediately following all contests in the regular season (and within 24 hours after regular season tournaments) and in the playoffs or be subject to a fine. -

National Championships Qualifying Standards
TRACK & FIELD COACHES MANUAL National Championships Qualifying Standards Timing: Meet directors must report performances as recorded/timed in the competition- if hand timed, report as a hand time to the tenth of a second; if fully automatic timed, report as F.A.T. to the hundredth of a second. DO NOT CONVERT HAND TIMES to F.A.T. Hand times are not accepted in events 200 meters or less. For qualification procedures, the most current USTFCCCA conversions for altitude and track size adjustments will be used. 2020 Indoor Track and Field Qualifying Standards MEN WOMEN Event Event # ”A” Standard / “B” Standard Event # ”A” Standard / “B” Standard 60 Meter Dash 1 6.88 / 6.93 22 7.72 / 7.82 60 Meter Hurdles 2 8.23 / 8.38 23 9.00/ 9.15 200 Meter Dash 3 22.26 / 22.38 24 25.60 / 25.90 400 Meter Run 4 49.55 / 50.00 25 58.40 / 59.40 600 Meter Run 5 1:22.00 / 1:22.80 26 1:37.50 / 1:38.70 800 Meter Run 6 1:55.95 / 1:56.90 27 2:18.00 / 2:19.85 1000 Meter Run 7 2:32.00 / 2:33.00 28 3:01.50 / 3:04.00 Mile Run 8 4:19.50 / 4:22.00 29 5:10.00 / 5:16.00 3,000 Meter Run 9 8:42.00 / 8:46.00 30 10:28.00 / 10.35.00 5,000 Meter Run 10 15:06.00 / 15:20.00 31 18:18.00 / 18:30.00 3000 Meter Walk 11 14:18.00 / 15:35.00 32 16:30.00 / 17:45.00 4 x 400 Meter Relay 12 3:21.00 / 3:22.50 33 4:00.00 / 4:03.00 4 x 800 Meter Relay 13 7:57.50 / 7:59.99 34 9:45.00 / 9:48.00 Distance Medley Relay (Meters) 14 10:24.00 / 10:26.00 35 12:33.00 / 12:38.00 Triple Jump 15 14.25m / 14.05m 36 11.40m / 11.15m Shot Put 16 15.75m / 15.25m 37 13.45m / 13.00m Pole Vault 17 4.75m/ 4.65m 38 3.52m / 3.42m Long Jump 18 7.10m / 7.00m 39 5.60m / 5.50m High Jump 19 2.04m / 2.01m 40 1.68m / 1.65m Weight Throw 20 17.10m / 16.25m 41 16.20m / 15.80m Heptathlon (M) / Pentathlon (W) 21 Top 16 declared – 4,150 min.