Spectral Distortions of the Cosmic Microwave Background Dissertation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Keenan Allen, Mike Williams and Austin Ekeler, and Will Also Have Newly-Signed 6 Sun ., Oct
GAME RELEASE PRESEASON WEEK 2 vs. SAN FRANCISCO 49ERS SUN. AUG. 22, 2021 | 4:30 PM PT bolts build under brandon staley 20212020 chargers schedule The Los Angeles Chargers take on the San Francisco 49ers for the 49th time ever PRESEASON (1-0) in the preseason, kicking off at 4:30 p m. PT from SoFi Stadium . Spero Dedes, Dan Wk Date Opponent TV Time*/Res. Fouts and LaDainian Tomlinson have the call on KCBS while Matt “Money” Smith, 1 Sat ., Aug . 14 at L .A . Rams KCBS W, 13-6 Daniel Jeremiah and Shannon Farren will broadcast on the Chargers Radio Network 2 Sun ., Aug . 22 SAN FRANCISCO KCBS 4:30 p .m . airwaves on ALT FM-98 7. Adrian Garcia-Marquez and Francisco Pinto will present the game in Spanish simulcast on Estrella TV and Que Buena FM 105 .5/94 .3 . 3 Sat ., Aug . 28 at Seattle KCBS 7:00 p .m . REGULAR SEASON (0-0) The Bolts unveiled a new logo and uniforms in early 2020, and now will be unveiling a revamped team under new head coach, Brandon Staley . Staley, who served as the Wk Date Opponent TV Time*/Res. defensive coordinator for the Rams in 2020, will begin his first year as a head coach 1 Sun ., Sept . 12 at Washington CBS 10:00 a .m . by playing against his former team in the first game of the preseason . 2 Sun ., Sept . 19 DALLAS CBS 1:25 p .m . 3 Sun ., Sept . 26 at Kansas City CBS 10:00 a .m . Reigning Offensive Rookie of the YearJustin Herbert looks to build off his 2020 season, 4 Mon ., Oct . -

Our School Preschool Songbook
September Songs WELCOME THE TALL TREES Sung to: “Twinkle, Twinkle, Little Star” Sung to: “Frère Jacques” Welcome, welcome, everyone, Tall trees standing, tall trees standing, Now you’re here, we’ll have some fun. On the hill, on the hill, First we’ll clap our hands just so, See them all together, see them all together, Then we’ll bend and touch our toe. So very still. So very still. Welcome, welcome, everyone, Wind is blowing, wind is blowing, Now you’re here, we’ll have some fun. On the trees, on the trees, See them swaying gently, see them swaying OLD GLORY gently, Sung to: “Oh, My Darling Clementine” In the breeze. In the breeze. On a flag pole, in our city, Waves a flag, a sight to see. Sun is shining, sun is shining, Colored red and white and blue, On the leaves, on the trees, It flies for me and you. Now they all are warmer, and they all are smiling, In the breeze. In the breeze. Old Glory! Old Glory! We will keep it waving free. PRESCHOOL HERE WE ARE It’s a symbol of our nation. Sung to: “Oh, My Darling” And it flies for you and me. Oh, we're ready, Oh, we're ready, to start Preschool. SEVEN DAYS A WEEK We'll learn many things Sung to: “For He’s A Jolly Good Fellow” and have lots of fun too. Oh, there’s 7 days in a week, 7 days in a week, So we're ready, so we're ready, Seven days in a week, and I can say them all. -
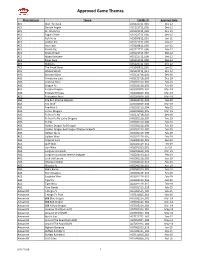
Approved Game Themes
Approved Game Themes Manufacturer Theme THEME ID Approval Date ACS Bust The Bank ACS121712_001 Dec-12 ACS Double Angels ACS121712_002 Dec-12 ACS Dr. Watts Up ACS121712_003 Dec-12 ACS Eagle's Pride ACS121712_004 Dec-12 ACS Fish Party ACS060812_001 Jun-12 ACS Golden Koi ACS121712_005 Dec-12 ACS Inca Cash ACS060812_003 Jun-12 ACS Karate Pig ACS121712_006 Dec-12 ACS Kings of Cash ACS121712_007 Dec-12 ACS Magic Rainbow ACS121712_008 Dec-12 ACS Silver Fang ACS121712_009 Dec-12 ACS Stallions ACS121712_010 Dec-12 ACS The Freak Show ACS060812_002 Jun-12 ACS Wicked Witch ACS121712_011 Dec-12 AGS Bonanza Blast AGS121718_001 Dec-18 AGS Chinatown Luck AGS121718_002 Dec-18 AGS Colossal Stars AGS021119_001 Feb-19 AGS Dragon Fa AGS021119_002 Feb-19 AGS Eastern Dragon AGS031819_001 Mar-19 AGS Emerald Princess AGS031819_002 Mar-19 AGS Enchanted Pearl AGS031819_003 Mar-19 AGS Fire Bull Xtreme Jackpots AGS021119_003 Feb-19 AGS Fire Wolf AGS031819_004 Mar-19 AGS Fire Wolf II AGS021119_004 Feb-19 AGS Forest Dragons AGS031819_005 Mar-19 AGS Fu Nan Fu Nu AGS121718_003 Dec-18 AGS Fu Nan Fu Nu Lucky Dragons AGS021119_005 Feb-19 AGS Fu Pig AGS021119_006 Feb-19 AGS Golden Dragon Red Dragon AGS021119_008 Feb-19 AGS Golden Dragon Red Dragon Xtreme Jackpots AGS021119_007 Feb-19 AGS Golden Skulls AGS021119_009 Feb-19 AGS Golden Wins AGS021119_010 Feb-19 AGS Imperial Luck AGS091119_001 Sep-19 AGS Jade Wins AGS021119_011 Feb-19 AGS Lion Wins AGS071019_001 Jul-19 AGS Longhorn Jackpots AGS031819_006 Mar-19 AGS Longhorn Jackpots Xtreme Jackpots AGS021119_012 Feb-19 AGS Luck -

George Paynter Career
Paner Family Baseball Family The Professional Baseball Life & Times of George W. Paynter (Paner) (“the ball player”) So we beat on, boats against the current, borne back ceaselessly into the past - The thing that connects us is love. 1 My Grandfather, George W. Paynter (Paner), was on his own from about age 13 (1884), after his Father died at age 31. 1800s generations spelling of Paner varied, but in Germanic Cincinnati they likely sounded alike. Throughout his pro baseball playing he was Paynter. He died when I was in the 4th Grade (1950). I only knew him from our one or two visits each year to see extended family in Cincinnati. I often heard - “ So you’re the Grandson of George Paner - the ball player”. Though his single game in the Major Leagues was 50+ years earlier “the ball player” title stuck due to his zest for playing more than 20 years, in and out of town, in very competitive pro and semi-pro leagues until age 42, and rooting for the beloved home town Reds all his life. Kevin Costner’s line in Field of Dreams - "I only knew him later, after life beat him down.", spoke of my Grandfather to me. George Paynter’s baseball and life story is compelling: • Strong semi-pro years, then briefly in minors at Lynchburg VA. (April, 1894) • “Cup of coffee” career single game in the National League (August 12, 1894) • Devastating Southern League game beaning ( August, 1896) • Patient in the South’s first Hospital for the Insane in Tuscaloosa, AL (1896) • Wife’s (my Grandmother) trip to gain his release and, teach him skills again • Losing George Jr at age 11, in a gruesome homicide (1905) • Playing another 15 years of very competitive pro / semi-pro baseball and loving the game a lifetime. -

\0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 X 1 Kampf ... \0-9\1, 2, 3
... \0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 x 1 Kampf ... \0-9\1, 2, 3 ... \0-9\1,000,000 ... \0-9\10 Pin ... \0-9\10... Knockout! ... \0-9\100 Meter Dash ... \0-9\100 Mile Race ... \0-9\100,000 Pyramid, The ... \0-9\1000 Miglia Volume I - 1927-1933 ... \0-9\1000 Miler ... \0-9\1000 Miler v2.0 ... \0-9\1000 Miles ... \0-9\10000 Meters ... \0-9\10-Pin Bowling ... \0-9\10th Frame_001 ... \0-9\10th Frame_002 ... \0-9\1-3-5-7 ... \0-9\14-15 Puzzle, The ... \0-9\15 Pietnastka ... \0-9\15 Solitaire ... \0-9\15-Puzzle, The ... \0-9\17 und 04 ... \0-9\17 und 4 ... \0-9\17+4_001 ... \0-9\17+4_002 ... \0-9\17+4_003 ... \0-9\17+4_004 ... \0-9\1789 ... \0-9\18 Uhren ... \0-9\180 ... \0-9\19 Part One - Boot Camp ... \0-9\1942_001 ... \0-9\1942_002 ... \0-9\1942_003 ... \0-9\1943 - One Year After ... \0-9\1943 - The Battle of Midway ... \0-9\1944 ... \0-9\1948 ... \0-9\1985 ... \0-9\1985 - The Day After ... \0-9\1991 World Cup Knockout, The ... \0-9\1994 - Ten Years After ... \0-9\1st Division Manager ... \0-9\2 Worms War ... \0-9\20 Tons ... \0-9\20.000 Meilen unter dem Meer ... \0-9\2001 ... \0-9\2010 ... \0-9\21 ... \0-9\2112 - The Battle for Planet Earth ... \0-9\221B Baker Street ... \0-9\23 Matches .. -
2019-04-24 Edition
Vote Rocky Shanehsaz For Noblesville City Council on May 7! Visionary. Collaborative. Community Focused. Learn more at RockyforCouncil.com Paid for by the Rocky For Council Campaign EDNESDAY PRIL TODAy’s WeaTHER W , A 24, 2019 Today: Partly sunny. Tonight: Partly to mostly cloudy. SHERIDAN | NOBLESVILLE | CICERO | ARCADIA Scattered showers or storms. IKE ATLANTA | WESTFIELD | CARMEL | FISHERS NEWS GATHERING L & PARTNER FOLLOW US! HIGH: 68 LOW: 54 Churches to stream services . County partners with Noblesville Prayer IMS for 500 Days of May Breakfast canceled over legal worries The REPORTER watch the service for those The Noblesville Prayer interested. Breakfast scheduled for The prayer breakfast May 2 at White River is held in conjunction with Christian Church has been the National Day of Prayer. canceled. Following the 2018 No- In lieu of the tradition- blesville Mayor’s Prayer al breakfast, many local Breakfast, the city turned churches have offered to the event organization over stream a Facebook Live to Helping Hands of No- prayer service that morning. blesville after receiving out- Once the event has been side pressure and potential organized, social media litigation over separation of will be used to share de- church and state – and those tails of when and where to concerns have resurfaced. Westfield launches Photo provided SafeRoads campaign Hamilton County Tourism is working with the Indianapolis Motor Speedway to connect with Hamilton County and local cities and celebrate the month of May. The IMS requests that the county fly the The REPORTER • Education: The City Indianapolis 500 flag during the entire month of May. On Monday, the Indy 500 flag was raised over On Tuesday, May- will implement ongo- the Courthouse. -

Licensed Gambling Operators 9-30-2020
9/30/2020 PROVIDED BY THE MONTANA DEPARTMENT OF JUSTICE, GAMBLING CONTROL DIVISION LICENSED GAMBLING OPERATORS and LICENSEES for FISCAL YEAR 2021 GROUPED BY COUNTY, CITY AND FINALLY BY LOCATION NAME. COUNTY: BEAVERHEAD CITY: DILLON 4040442-004-GOA 15 Licensed Machine(s) BLACKTAIL STATION 26 S MONTANA ST DILLON MT 59725 Licensee: BLACKTAIL STATION INC 4065304-003-GOA 2 Licensed Machine(s) CLUB BAR 134 N MONTANA ST DILLON MT 59725 Licensee: CLUB BAR 6429929-004-GOA 5 Licensed Machine(s) GATEWAY CANYON TRAVEL PLAZA 4055 REBICH LN DILLON MT 59725 Licensee: GATEWAY CANYON TRAVEL PLAZA INC. 6665116-003-GOA 9 Licensed Machine(s) GOLDEN BAR & CASINO 8 N MONTANA ST DILLON MT 59725 Licensee: GOLDEN BAR & CASINO, LLC 6329932-002-GOA 11 Licensed Machine(s) KLONDIKE INN 33 E BANNACK ST DILLON MT 59725 Licensee: CKI, LLC 6460969-004-GOA 5 Licensed Machine(s) KNOTTY PINE TAVERN 17 E BANNACK ST DILLON MT 59725 Licensee: B & R ENTERPRISES LLC 4091300-008-GOA 20 Licensed Machine(s) LUCKY LIL'S CASINO OF DILLON 635 N MONTANA ST DILLON MT 59725 Licensee: DILLON CASINO INC 4145194-013-GOA 20 Licensed Machine(s) MAGIC DIAMOND CASINO OF DILLON 101 E HELENA ST DILLON MT 59725 Licensee: TOWN PUMP OF HARLOWTOWN INC WEB-MT_mr011 Page 1 of 191 9/30/2020 PROVIDED BY THE MONTANA DEPARTMENT OF JUSTICE, GAMBLING CONTROL DIVISION LICENSED GAMBLING OPERATORS and LICENSEES for FISCAL YEAR 2021 GROUPED BY COUNTY, CITY AND FINALLY BY LOCATION NAME. COUNTY: BEAVERHEAD CITY: DILLON 6718975-003-GOA 4 Licensed Machine(s) OFFICE BAR 21 E BANNACK ST DILLON MT 59725 Licensee: ZTIK -

Karaoke Song Book Karaoke Nights Frankfurt’S #1 Karaoke
KARAOKE SONG BOOK KARAOKE NIGHTS FRANKFURT’S #1 KARAOKE SONGS BY TITLE THERE’S NO PARTY LIKE AN WAXY’S PARTY! Want to sing? Simply find a song and give it to our DJ or host! If the song isn’t in the book, just ask we may have it! We do get busy, so we may only be able to take 1 song! Sing, dance and be merry, but please take care of your belongings! Are you celebrating something? Let us know! Enjoying the party? Fancy trying out hosting or KJ (karaoke jockey)? Then speak to a member of our karaoke team. Most importantly grab a drink, be yourself and have fun! Contact [email protected] for any other information... YYOUOU AARERE THETHE GINGIN TOTO MY MY TONICTONIC A I L C S E P - S F - I S S H B I & R C - H S I P D S A - L B IRISH PUB A U - S R G E R S o'reilly's Englische Titel / English Songs 10CC 30H!3 & Ke$ha A Perfect Circle Donna Blah Blah Blah A Stranger Dreadlock Holiday My First Kiss Pet I'm Mandy 311 The Noose I'm Not In Love Beyond The Gray Sky A Tribe Called Quest Rubber Bullets 3Oh!3 & Katy Perry Can I Kick It Things We Do For Love Starstrukk A1 Wall Street Shuffle 3OH!3 & Ke$ha Caught In Middle 1910 Fruitgum Factory My First Kiss Caught In The Middle Simon Says 3T Everytime 1975 Anything Like A Rose Girls 4 Non Blondes Make It Good Robbers What's Up No More Sex.... -

Notre Dame Scholastic, Vol. 109, No. 08
SCHOLASTIC NOVEMBER 17^ 1967 AU)Abiv gYBirgirg B'0'0'o"o'oT^Tro"oT>TyrgTnnnnnn: lamptti^^hop i"o"6 0 60 0 0 oinnnnnnrB o"o"a"o"6"aoa"6"o"a"o"OTii;; Perfect for the weather that's here . i and the weather to come THE GENUINE Lonoon F06 MAINCOAT ® Weather, even Michiana weather, poses no ]Droblem for the Maincoat® with its zip-in liner of 100% Alpaca. The shell is 65% Dacron*/35% cotton for wash and wear convenience and, as an added feature, the entire coat is treated with Ze Pel* for re sistance to stains. This coat serves you long and well. In Oyster, Natural and Black. $60 *DuPont's reg. T.M. Stop m and browse . it's YOUR store! ldL9JL9.ft.9.g..9.9.9.g ft 9 9 ft I GILBERT'S 19.9.9.9.9.9,9.9 9 9.9.9.9,9,9JU>J>^ ON THE CAMPUS . NOTRE DAME yaTa'a~o"tfTro"o"o"a"a~o~gTnnTnnmnnnnnjTn n ro'o'o'o'o'oo 0 0 0 0 eiro'o~o'o'o'o'o'o'o"o'o oo o o a Ox Ifs a small price to pay . PALM BEACH 4-PIECE TRIP-L-AIRE A complete wardrobe! You enjoy a 100% Avool, natural shoulder herring bone suit, with vest, plus a pair of solid color-coordinated slacks ... by mixing and matching you have an outfit for sports, dress or leisure. Choose yours from Gray or Olive tones. $85 Trip-L-Aire engineered by Palm Beach We invite you to select and wear your apparel now . -

Remembering Gallipoli
Produced by Wigan Museums & Archives Issue No. 69 April-July 2015 REMEMBERING GALLIPOLI £2 Visit Wigan Borough Museums & Archives ARCHIVES & MUSEUMS Contents Letter from the 4-5 Love Laughs at Blacksmiths Editorial Team 6-7 Leigh Shamrocks Welcome to PAST Forward Issue 69 . 8-9 Remembering Local You will find in this edition the joint second placed articles – by Thomas Men at Gallopoli McGrath and Alf Ridyard – from the Past Forward Essay Competition, kindly sponsored by Mr and Mrs John O’Neill and the Wigan Borough Environment 10-11 News from the and Heritage Network. The 2015 Competition is now open (see opposite Archives page for information), so please get in touch if you would like more details 12-13 Genealogical or to submit an entry. Experience Elsewhere in the magazine you will find the concluding part of a history of 14-15 Half-Timers Gullick Dobson in Wigan, a look through the family tree of highwayman, George Lyon and our commemoration of the 100th anniversary of the 16-17 Collections Corner Gallipoli landings in 1915. 18-19 The Lancashire We're pleased to announce that audio versions of Past Forward will again by Collier Girl available by subscription. Working with Wigan Talking News we hope to launch this service in the coming months. Please contact us for more details. 20-22 Gullick Dobson There is much to look forward to at the Museums and Archives in the 23 A Poppy for Harry coming months, including two new temporary exhibitions at the Museum – 24-25 The Enigma that was A Potter’s Tale and our Ancient Egypt Exhibition – the re-launch of our George Lyon online photographic gallery with new First World War resources and a major new cataloguing project at the Archives funded by the Wellcome Trust. -

Results Sporting Retrievers (Golden) 22 BB/G1/RBIS GCHS CH Blueprint's Sweetgold Country Girl
Plum Creek Kennel Club of Colorado Friday, June 11, 2021 Group Results Sporting Retrievers (Golden) 22 BB/G1/RBIS GCHS CH Blueprint's Sweetgold Country Girl. SS06663202 Pointers (German Shorthaired) 12 BB/G2 GCH CH Summit's Four Fans Of Freedom JH. SS01719501 Setters (English) 7 BB/G3 GCHS CH Seamrog Spitfire. SR83127601 Pointers 7 BB/G4 GCHB CH Solivia's Whatever Turns You On. SS01774802 Hound Dachshunds (Wirehaired) 15 BB/G1 GCH CH Benway's Garnet Cut Mw. HP57867101 Salukis 21 BB/G2 GCH CH Issibaa's Llarkin. HP56058603 Borzois 19 BB/G3 GCH CH Kyrov's Sword Dance. HP52959501 Basset Hounds 12 BB/G4 GCHS CH First Class Toast To Empress Sisi. HP52492103 Working Boxers 17 BB/G1/BIS GCHG CH Galaroc N Black Dymond's Gonna Get Real. WS57895701 Bernese Mountain Dogs 31 BB/G2 CH Cor Caroli's Mission to the Stars CD RN. WS56230101 Cane Corso 11 BB/G3 GCH CH Castleguard's Lust For Life. WS67947901 Bullmastiffs 10 BB/G4 GCHB CH T-Boldt's These Boots Are Made For Walkin. WS61531103 Terrier Miniature Schnauzers 9 BB/G1 GCHB CH Laroh's I Ain'T Kidding. RN31868501 Staffordshire Bull Terriers 11 BB/G2 GCHS CH Juggernaut's Chart A Course Sulu. RN29075103 Cairn Terriers 7 BB/G3 GCHB CH Fom's Number One Small Caliber Bullet Of Ctc RN29162402 West Highland White Terriers 17 BB/G4 GCHS CH Snowy River's Trail Rider. RN29921801 Toy Silky Terriers 7 BB/G1 CH Double U's Ace In The Hole. TS34211401 Manchester Terriers (Toy) 5 BB/G2 GCHS CH Passport Sunkissed It's A Yes From Me Bonchien. -

NICHOLS-BRISTOL, Inc. B I N G O RANGE HILL TURKEY FARMI
l/ i. TUESDAT, NOVEMBER 18,1847 ThffWaatlMr 0tancii^0ttr E o r t t f n g Avaraga Dolly CIrcalatioa i a t u .a Waofta Far tbs Manth a f Odahsr. 1663 T OuOd win hava^ DalU'Chaptar,, No. 8L ------------ Me tha yuar sa fdOews: 9,311 all*day aeaaion Thursday from ten win eonfer the dadegms of Moot Ba< Eoiarfencjr Doetors PTA Meeting Kindargarten. Mrs. Alan O n aad 1 o’cieu on. to work on articles for oellaat Master at their regular Mra. Aaron Ooek; P in t Orada, hae af tha As«H convocation Wednesday evening, Mrs. Richard'QuUUtch and Mrs. tlM sale December 4. The mem Dr. Alfred Sundqulst end Dr, ■ s a il bers are to brinC their own bos November 16. Light refreshments Of Green Unit Charles KlotMr; Second Grade, will be served at the close cf the Robert Wsteon of the Manches Manehaster^A Ciiy of ViUaga Charm luncbos and dissert and coffee ter Medical Aasodation are the Mrs. OUmour Oole; Third Grads, will bs sarred. Chapter. physiciana .who will respond to Mrs. Donald Makqteace; Pourth PRICE TOUR CENTS f Grade, Mrs. Rajnaond Behaller; (TWENTY PAGES) The Mothers Circle o f the emergency calls tomorrow aft Outstanding Speaker Se AfhraelMig an IB) MANCltESTER, CONN„ WEDNESDAY, NOVEMBER 19,1947 Anderson Shea Post No. 136. ernoon. Fifth Grade, Mr& Richard McCar VOL. LXVIL, NO. 43 Veterans of Porelffn Wars, will Sacred Heart Win meet Thursday cured for Tomorrow thy; Sixth Grade, Mrs. Alan HeU- meet at the post home tonight at evening at 6:15 at the home of strom; Seventh Grade, Mrs.