The Long-Lasting Shadow of the Allied Occupation of Austria on Its Spatial Equilibrium
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Changing Depiction of Prussia in the GDR
The Changing Depiction of Prussia in the GDR: From Rejection to Selective Commemoration Corinna Munn Department of History Columbia University April 9, 2014 Acknowledgments I would like to thank my advisor, Volker Berghahn, for his support and guidance in this project. I also thank my second reader, Hana Worthen, for her careful reading and constructive advice. This paper has also benefited from the work I did under Wolfgang Neugebauer at the Humboldt University of Berlin in the summer semester of 2013, and from the advice of Bärbel Holtz, also of Humboldt University. Table of Contents 1. Introduction……………………………………………………………………….1 2. Chronology and Context………………………………………………………….4 3. The Geschichtsbild in the GDR…………………………………………………..8 3.1 What is a Geschichtsbild?..............................................................................8 3.2 The Function of the Geschichtsbild in the GDR……………………………9 4. Prussia’s Changing Role in the Geschichtsbild of the GDR…………………….11 4.1 1945-1951: The Post-War Period………………………………………….11 4.1.1 Historiography and Publications……………………………………11 4.1.2 Public Symbols and Events: The fate of the Berliner Stadtschloss…14 4.1.3 Film: Die blauen Schwerter………………………………………...19 4.2 1951-1973: Building a Socialist Society…………………………………...22 4.2.1 Historiography and Publications……………………………………22 4.2.2 Public Symbols and Events: The Neue Wache and the demolition of Potsdam’s Garnisonkirche…………………………………………..30 4.2.3 Film: Die gestohlene Schlacht………………………………………34 4.3 1973-1989: The Rediscovery of Prussia…………………………………...39 4.3.1 Historiography and Publications……………………………………39 4.3.2 Public Symbols and Events: The restoration of the Lindenforum and the exhibit at Sans Souci……………………………………………42 4.3.3 Film: Sachsens Glanz und Preußens Gloria………………………..45 5. -

Knji\236Ica the Parnassus
Programme 6 Tursday, 15 October 9.15–12.00 Welcoming Address Archduke Ferdinand and His Musical Parnassus Vanja Kočevar (Ljubljana, Slovenia) Archduke Ferdinand of Inner Austria: From an Insignifcant Prince on the Periphery of the Holy Roman Empire to Emperor and a Central Figure in Early Seventeenth-Century European Politics Metoda Kokole (Ljubljana, Slovenia) Archduke Ferdinand’s Musical Parnassus in Graz — cofee — Ferdinand’s Musical Repertoire Marina Toffetti (Padua, Italy) From Milan to Graz: Milanese Composers in the Parnassus Musi- cus Ferdinandaeus Klemen Grabnar (Ljubljana, Slovenia) Pietro Antonio Bianco’s Missa Percussit Saul mille: A Musical Souvenir in Graz of Archduke Ferdinand’s Visit to Italy 7 — lunchtime break — 14.30–17.30 Te Musical Establishments of the Polish, Bavarian, and Transylvanian Courts Barbara Przybyszewska-Jarmińska (Warsaw, Poland) Music-Related Contacts Between the Courts of the Polish King and the Archdukes of Inner Austria (1592–1619) and the Dissemi- nation of musica moderna in Central and East-Central Europe Britta Kägler (Munich, Germany) An Italianate Court Chapel? Foreign Musicians at the Ducal Court of Munich at the Turn of the Sixteenth Century Peter Király (Kaiserslautern, Germany) Foreign Musicians at the Transylvanian Court of Sigismund Báthory — cofee — Te Habsburgs Michaela Žáčková Rossi (Prague, Czech Republic) “[…] questo Bassista è buona persona […]”: Te End of the Im- perial Musicians’ Service 8 Tomasz Jeż (Warsaw, Poland) Te Music Patronage of Habsburg Family in Jesuit Silesia concert at 20.00 Friday, 16 October 9.00–12.30 Composers of the Parnassus Musicus Ferdinandaeus Aleksandra Patalas (Kraków, Poland) G. B. Cocciola’s Presence in the Parnassus and His Activity in the Polish-Lithuanian Commonwealth Herbert Seifert (Vienna, Austria) Giovanni Sansoni (c. -

M1928 1945–1950
M1928 RECORDS OF THE GERMAN EXTERNAL ASSETS BRANCH OF THE U.S. ALLIED COMMISSION FOR AUSTRIA (USACA) SECTION, 1945–1950 Matthew Olsen prepared the Introduction and arranged these records for microfilming. National Archives and Records Administration Washington, DC 2003 INTRODUCTION On the 132 rolls of this microfilm publication, M1928, are reproduced reports on businesses with German affiliations and information on the organization and operations of the German External Assets Branch of the United States Element, Allied Commission for Austria (USACA) Section, 1945–1950. These records are part of the Records of United States Occupation Headquarters, World War II, Record Group (RG) 260. Background The U.S. Allied Commission for Austria (USACA) Section was responsible for civil affairs and military government administration in the American section (U.S. Zone) of occupied Austria, including the U.S. sector of Vienna. USACA Section constituted the U.S. Element of the Allied Commission for Austria. The four-power occupation administration was established by a U.S., British, French, and Soviet agreement signed July 4, 1945. It was organized concurrently with the establishment of Headquarters, United States Forces Austria (HQ USFA) on July 5, 1945, as a component of the U.S. Forces, European Theater (USFET). The single position of USFA Commanding General and U.S. High Commissioner for Austria was held by Gen. Mark Clark from July 5, 1945, to May 16, 1947, and by Lt. Gen. Geoffrey Keyes from May 17, 1947, to September 19, 1950. USACA Section was abolished following transfer of the U.S. occupation government from military to civilian authority. -

Austrians Are Most Concerned About Health and Long-Term Care
O E C D Risks That Matter Survey 2020 AUSTRIA July 2021 www.oecd.org/social/risks-that-matter.htm Austrians are most concerned about health and long-term care The OECD’s cross-national Risks that Matter Yet almost 60% of Austrians also say they Fig. 2. Share of respondents identifying survey examines people’s perceptions of worry about LTC for themselves. personal networks as their primary source of support in case of financial difficulty social and economic risks and how well they Like respondents in most other countries, feel their government reacts to their concerns. Austrians are more likely to count on friends % The survey polled a representative sample of and family than on government to support 70 25000 people aged 18 to 64 years old in 25 them through financial difficult (Fig. 2). And 60 OECD countries to understand better what over 60% of Austrians say that government 50 citizens want and need from social policy – should be doing more or much more to 40 particularly in the face of the COVID-19 support their economic and social security, 30 pandemic. relative to a 68% average across the OECD. 20 Over 80% of respondents in Austria report that When evaluating specific social programmes, 10 their country’s economic situation worsened a slim majority of Austrians agree or strongly 0 during the pandemic, compared to a cross- AUT OECD DNK SVN agree with having good access to healthcare national average of 71% (Fig. 1). This – a noteworthy outcome considering the economic sentiment is also reflected in the health exigencies of the pandemic and the Fig. -

Exile and Holocaust Literature in German and Austrian Post-War Culture
Religions 2012, 3, 424–440; doi:10.3390/rel3020424 OPEN ACCESS religions ISSN 2077-1444 www.mdpi.com/journal/religions Article Haunted Encounters: Exile and Holocaust Literature in German and Austrian Post-war Culture Birgit Lang School of Languages and Linguistics, The University of Melbourne, Parkville 3010 VIC, Australia; E-Mail: [email protected] Received: 2 May 2012; in revised form: 11 May 2012 / Accepted: 12 May 2012 / Published: 14 May 2012 Abstract: In an essay titled ‗The Exiled Tongue‘ (2002), Nobel Prize winner Imre Kertész develops a genealogy of Holocaust and émigré writing, in which the German language plays an important, albeit contradictory, role. While the German language signified intellectual independence and freedom of self-definition (against one‘s roots) for Kertész before the Holocaust, he notes (based on his engagement with fellow writer Jean Améry) that writing in German created severe difficulties in the post-war era. Using the examples of Hilde Spiel and Friedrich Torberg, this article explores this notion and asks how the loss of language experienced by Holocaust survivors impacted on these two Austrian-Jewish writers. The article argues that, while the works of Spiel and Torberg are haunted by the Shoah, the two writers do not write in the post-Auschwitz language that Kertész delineates in his essays, but are instead shaped by the exile experience of both writers. At the same time though, Kertész‘ concept seems to be haunted by exile, as his reception of Jean Améry‘s works, which form the basis of his linguistic genealogies, shows an inability to integrate the experience of exile. -

Republik Oesterreich
REPUBLIK ÖSTERREICH Organe der Bundesgesetzgebung. Wien, I/1, Parlamentsring 3, Tel. A19-500/9 Serie, A24-5-75. Dienststunden: Montag bis Freitag von 8 bis 16 Uhr, Samstag von 8 bis 12 Uhr. Nationalrat. Präsident: Leopold Kunschak. Zweiter Präsident: Johann Böhm. Dritter Präsident: Dr. Alfons Gorbach. Mitglieder. Cerny Theodor, Steinmetz- _ Scheff Otto, Dr., Rechtsanwalt; meister; Gmünd. ÖVP. Maria-Enzersdorf. ÖVP. (LB. = LirLksblock, Kommunistische Partei Österreichs. Dengler Josef, Arbeitersekretär; Scheibenreif Alois, Bauer; ÖVP. = Österreichische Volkspartei. — Wien. ÖVP. Reith 5 bei Neunkirchen. ÖVP. SPÖ. = Sozialistische Partei Österreichs. — VdU. = Verband der Unabhängigen.) Ehrenfried Anton, Beamter; Schneeberger Pius, Forstarbeiter; Hollabrunn. ÖVP. Wien. Burgenland. Eichinger Karl, Bauer; Wind— _ Seidl Georg, Bauer; Gaubitsch 76, passing 6. ÖVP. Post Unterstinkenbrunn. ÖVP Böhm Johann, Zweiter Präsident des Nationalrates; Wien. SPÖ. Figl Leopold, Dr. h. c., Ing., Singer Rudolf, Aufzugsmonteur; Bundeskanzler; Wien. ÖVP. St. Pölten. SPÖ. Frisch Anton, Hofrat, Landes— schulinspektor; Wien, ÖVP. Fischer Leopold, Weinbauer; Solar Lola, Fachlehrerin; Wien- Sooß, Post Baden bei Wien. ÖVP. Mödling. ÖVP. Nedwal Andreas, Landwirt; Gerersdorf bei Güssing. ÖVP. Floßmann Ferdinanda. Strasser Peter, Techniker; Wien. SPÖ. Privatangestellte; Wien. SPÖ. Nemecz Alexander, Dr., Rechts- Strommer Josef, Bauer; Mold 4, anwalt; Oberwarth 119 b. ÖVP. Frühwirth Michael, Textilarbeiter; Post Horn. Wien-Atzgersdorf. SPÖ. Proksch Anton, Leitender Sekretär Tschadck Otto, Dr., Bundes— des ÖGB.; Wien. SPÖ. Gasmlich Anton, Dr., Professor; Wien, VdU. minister für Justiz; Wien, SPÖ. Rosenberger Paul, Landwirt; Wallner Josef, Holzgroßhändler; DeutschJahrndorf 169. SPÖ. Gindler Anton, Bauer; Perndorf 13, Post Schweiggers. ÖVP. Amstetten, ÖVP. Strobl Franz, Ing., Landes- Widmayer Heinrich, Verwalter; forstdirektor; Wien. ÖVP. Gschweidl Rudolf, Lagerhalter; Puchberg am Schneeberg, Sier— Wien. -
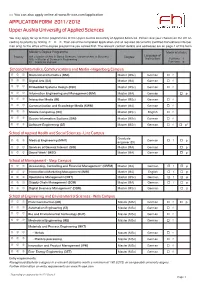
APPLICATION FORM 2011/2012 Upper Austria University of Applied Sciences
>> You can also apply online at www.fh-ooe.com/application APPLICATION FORM 2011/2012 Upper Austria University of Applied Sciences You may apply for up to three programmes at the Upper Austria University of Applied Sciences. Please rank your choices on the left ac- cording to priority by ticking . Then send the completed application and all required documents (certified translations into Ger- man only) to the office of the degree programme you ranked first. The relevant contact details and addresses are on page 4 of this form. Master‘s Degree Programme Mode of study: Priority MA = Master of Arts in Social Sciences, Master of Arts in Business Degree: Language of MSc = Master of Science in Engineering instruction: Full-time = f DI = Graduate engineer Part-time = p School of Informatics, Communications and Media - Hagenberg Campus Biomedical Informatics (BMI) Master (MSc) German f Digital Arts (DA) Master (MA) German f Embedded Systems Design (ESD) Master (MSc) German f Information Engineering and Management (IEM) Master (MA) German p Interactive Media (IM) Master (MSc) German f Communication and Knowledge Media (KWM) Master (MA) German f Mobile Computing (MC) Master (MSc) English f Secure Information Systems (SIM) Master (MSc) German f Software Engineering (SE) Master (MSc) German f p* School of Applied Health and Social Sciences - Linz Campus Graduate Medical Engineering (MMT) German f p engineer (DI) Services of General Interest (SGI) Master (MA) German p Social Work* (MSO) Master (MA) -

Building an Unwanted Nation: the Anglo-American Partnership and Austrian Proponents of a Separate Nationhood, 1918-1934
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Carolina Digital Repository BUILDING AN UNWANTED NATION: THE ANGLO-AMERICAN PARTNERSHIP AND AUSTRIAN PROPONENTS OF A SEPARATE NATIONHOOD, 1918-1934 Kevin Mason A dissertation submitted to the faculty of the University of North Carolina at Chapel Hill in partial fulfillment of the requirements for the degree of PhD in the Department of History. Chapel Hill 2007 Approved by: Advisor: Dr. Christopher Browning Reader: Dr. Konrad Jarausch Reader: Dr. Lloyd Kramer Reader: Dr. Michael Hunt Reader: Dr. Terence McIntosh ©2007 Kevin Mason ALL RIGHTS RESERVED ii ABSTRACT Kevin Mason: Building an Unwanted Nation: The Anglo-American Partnership and Austrian Proponents of a Separate Nationhood, 1918-1934 (Under the direction of Dr. Christopher Browning) This project focuses on American and British economic, diplomatic, and cultural ties with Austria, and particularly with internal proponents of Austrian independence. Primarily through loans to build up the economy and diplomatic pressure, the United States and Great Britain helped to maintain an independent Austrian state and prevent an Anschluss or union with Germany from 1918 to 1934. In addition, this study examines the minority of Austrians who opposed an Anschluss . The three main groups of Austrians that supported independence were the Christian Social Party, monarchists, and some industries and industrialists. These Austrian nationalists cooperated with the Americans and British in sustaining an unwilling Austrian nation. Ultimately, the global depression weakened American and British capacity to practice dollar and pound diplomacy, and the popular appeal of Hitler combined with Nazi Germany’s aggression led to the realization of the Anschluss . -

The Failed Post-War Experiment: How Contemporary Scholars Address the Impact of Allied Denazification on Post-World War Ii Germany
John Carroll University Carroll Collected Masters Essays Master's Theses and Essays 2019 THE FAILED POST-WAR EXPERIMENT: HOW CONTEMPORARY SCHOLARS ADDRESS THE IMPACT OF ALLIED DENAZIFICATION ON POST-WORLD WAR II GERMANY Alicia Mayer Follow this and additional works at: https://collected.jcu.edu/mastersessays Part of the History Commons THE FAILED POST-WAR EXPERIMENT: HOW CONTEMPORARY SCHOLARS ADDRESS THE IMPACT OF ALLIED DENAZIFICATION ON POST-WORLD WAR II GERMANY An Essay Submitted to the Office of Graduate Studies College of Arts & Sciences of John Carroll University in Partial Fulfillment of the Requirements for the Degree of Master of Arts By Alicia Mayer 2020 As the tide changed during World War II in the European theater from favoring an Axis victory to an Allied one, the British, American, and Soviet governments created a plan to purge Germany of its Nazi ideology. Furthermore, the Allies agreed to reconstruct Germany so a regime like the Nazis could never come to power again. The Allied Powers met at three major summits at Teheran (November 28-December 1,1943), Yalta (February 4-11, 1945), and Potsdam (July 17-August 2, 1945) to discuss the occupation period and reconstruction of all aspects of German society. The policy of denazification was agreed upon by the Big Three, but due to their political differences, denazification took different forms in each occupation zone. Within all four Allied zones, there was a balancing act between denazification and the urgency to help a war-stricken population in Germany. This literature review focuses specifically on how scholars conceptualize the policy of denazification and its legacy on German society. -

The Employment Effects of Immigration: Evidence from the Mass Arrival of German Expellees in Post-War Germany
The Employment Effects of Immigration: Evidence from the Mass Arrival of German Expellees in Post-war Germany By Sebastian Braun and Toman Omar Mahmoud No. 1725| August 2011 Kiel Institute for the World Economy, Hindenburgufer 66, 24105 Kiel, Germany Kiel Working Paper No. 1725 | August 2011 The Employment Effects of Immigration: Evidence from the Mass Arrival of German Expellees in Post-war Germany* Sebastian Braun and Toman Omar Mahmoud Abstract: This paper studies the employment effects of the influx of millions of German expellees to West Germany after World War II. The expellees were forced to relocate to post-war Germany. They represented a complete cross-section of society, were close substitutes to the native West German population, and were very unevenly distributed across labor market segments in West Germany. We find a substantial negative effect of expellee inflows on native employment. The effect was, however, limited to labor market segments with very high inflow rates. IV regressions that exploit variation in geographical proximity and in pre-war occupations confirm the OLS results. Keywords: Forced migration, native employment, post-war Germany JEL classification: J61, J21, C36 Sebastian Braun Kiel Institute for the World Economy Telephone: +49 431 8814 482 E-mail: [email protected] Toman Omar Mahmoud Kiel Institute for the World Economy Telephone: +49 431 8814 471 E-mail: [email protected] * We thank Eckhardt Bode, Michael C. Burda, Michael Kvasnicka, Alexandra Spitz-Oener, Andreas Steinmayr, Nikolaus Wolf and participants of research seminars in Berlin and Kiel for helpful comments and discussions. Martin Müller-Gürtler and Richard Franke provided excellent research assistance. -

Religious Determinants of Demographic Events
VIENNA INSTITUTE OF DEMOGRAPHY Working Papers 01 / 2006 Anne Goujon, Vegard Skirbekk, Katrin Fliegenschnee, Pawel Strzelecki New Times, Old Beliefs: Projecting the Future Size of Religions in Austria Vienna Institute of Demography Austrian Academy of Sciences Prinz Eugen-Straße 8-10 · A-1040 Vienna · Austria E-Mail: [email protected] Website: www.oeaw.ac.at/vid Abstract Projecting the religious composition of the population is relevant for several reasons. It is a key characteristic influencing several aspects of individual behaviour, including marriage and childbearing patterns. The religious composition is also a driver of social cohesion and increased religious diversity could imply a more fragmented society. In this context, Austria finds itself in a period of transition where the long-time dominant Roman-Catholic church faces a serious decline in membership, while other groups, particularly the seculars and the Muslims, increase their influence. We project religions in Austria until 2051 by considering relative fertility rates, religion-specific net migration, and the rate of conversion between religions and transmission of religious beliefs from parents to children. We find that the proportion of Roman Catholics is likely to decrease from 75% in 2001 to less than 50% by the middle of the century, unless current trends in fertility, secularisation or immigration are to change. The share of Protestants is estimated to reach a level between 3 and 5% in 2051. The most uncertain projections are for those without religious affiliation: they could number as little as 10% and as many as 33%. The Muslim population—which grew from 1% in 1981 to 4% in 2001—will, according to our estimates, represent 14 to 26% of the population by 2051. -

Raum Baden Zwischen 1933 Und März 1938. Fallbeispiel
DIPLOMARBEIT Titel der Diplomarbeit „Raum Baden zwischen 1933 und März 1938. Fallbeispiel Baden und Traiskirchen (Möllersdorf)“ Verfasserin Veronika Oeller angestrebter akademischer Grad Magistra der Philosophie (Mag. phil.) Wien, 2011 Studienkennzahl lt. Studienblatt: A190 313 299 Studienrichtung lt. Studienblatt: Lehramtsstudium UF Geschichte, Sozialkunde, Politische Bildung; UF Psychologie und Philosophie Betreuerin / Betreuer: Univ.-Doz. Fr. Dr. Irene Bandhauer-Schöffmann Danksagung Besonderen Dank an meine Eltern, für ihre Unterstützung, ihr Vertrauen und ihre Geduld. Ebenso bedanke ich mich bei meinen Freunden und Verwandten, die mich moralisch immer aufgebaut haben. Herzlichen Dank an Univ.- Doz. Fr. Dr. Irene Bandhauer-Schöffmann für ihr Engagement bei meiner Betreuung für die Diplomarbeit. Danke auch die Leiter und MitarbeiterInnen der verschiedenen Archive, die mir die Arbeit im Archiv erleichtert haben Inhaltsverzeichnis 1 EINLEITUNG .......................................................................................................................... 1 1.1 ÜBERBLICK ÜBER DIE POLITISCHE ENTWICKLUNG IN ÖSTERREICH WÄHREND DER 1930 ER JAHRE ...................................................................................................................................... 4 2 WIRTSCHAFT UND KRISE ...................................................................................................... 9 2.1 DER KURBETRIEB IN BADEN ............................................................................................ 11 2.2