DOCSLIB.ORG

Front Matter.1.1

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Front Matter.1.1 CANADIAN MATHEMATICS EDUCATION STUDY GROUP GROUPE CANADIEN D’ETUDE´ EN DIDACTIQUE DES MATHEMATIQUES´ PROCEEDINGS / ACTES 2003 ANNUAL MEETING Acadia University May 30 – June 3, 2003 EDITED BY: Elaine Simmt, University of Alberta Brent Davis, University of Alberta CANADIAN MATHEMATICS EDUCATION STUDY GROUP GROUPE CANADIEN D’ETUDE´ EN DIDACTIQUE DES MATHEMATIQUES´ PROCEEDINGS / ACTES 2003 ANNUAL MEETING Acadia University May 30 – June 3, 2003 EDITED BY: Elaine Simmt, University of Alberta Brent Davis, University of Alberta Proceedings of the 2003 Annual Meeting of the Canadian Mathematics Education Study Group / Groupe Canadien d’Étude en Didactique des Mathématiques are published by CMESG/GCEDM. They were printed in April 2004 in Edmonton, AB. Proceedings of the 2003 Annual Meeting of the Canadian Mathematics Education Study Group / Groupe Canadien d’Etude´ en Didactique des Mathématiques 27th Annual Meeting Acadia University May 30 – June 3, 2003 Contents / Table des matières v Acknowledgements vii Schedule MALGORZATA DUBIEL ix Introduction xi Special Announcement: Zoltan Dienes, Extraordinary Member of CMESG/GCEDM Plenary Lectures / Conférences plénières TOM ARCHIBALD 3 Using History of Mathematics in the Classroom: Prospects and Problems ANNA SIERPINSKA 11 Research in Mathematics Education Through a Keyhole Working Groups / Groupes de travail LOUIS CHARBONNEAU 39 A •L’histoire des mathématiques en tant que levier pédagogique & IRENE PERCIVAL au primaire et au secondaire / The History of Mathematics as a Pedagogic Tool in Grades K–12 FLORENCE GLANFIELD, LOUISE 55 B • Teacher Research: An Empowering Practice? POIRIER, & VICKI ZACK MIROSLAV LOVRIC 69 C • Images of Undergraduate Mathematics & DAVID POOLE WALTER WHITELY 79 D • A Mathematics Curriculum Manifesto & BRENT DAVIS Topic Sessions / Sessions thématiques MALGORZATA DUBIEL 87 A Report on the Canadian School Mathematics Forum 2003 ZOLTAN DIENES 91 The Theory of Six Stages in Learning with Integers JO TOWERS 103 Exploring the Fragility and Robustness of Students’ Mathematical Understanding JOHN GRANT McLOUGHLIN 111 The Role of Mathematics Contests iii New PhD Reports / Présentations de thèses de doctorat FRANCE CARON 119 Effects of Secondary Education on Mathematical Competencies: An Exploratory Study ALEX LAWSON 125 Documenting the Nature and Degree of Reform Instruction in the Intermediate Classroom JOYCE MGOMBELO 131 Mathematics Content-Pedagogy Knowledge: A Psychoanalytic and Enactivist Approach EILEEN PHILLIPS 139 Classroom Explorations of Mathematical Writing with Nine- and Ten-Year-Olds Ad Hoc Sessions / Séances ad hoc RINA COHEN 147 Empowering Math-Anxious, Upper Elementary Teachers in Over- coming Their Anxiety and Improving Their Teaching: An Explor- atory Study GARY FLEWELLING 149 MOM, Sense Making and Rich Learning Tasks RICHARD HOSHINO 151 A “Proof” that all Triangles are Equilateral: Drawing out the Math- ematics from a Rich Investigative Problem IMMACULATE NAMUKASA 153 Multiple Meanings: Why Should We Encourage Their Use? Panel Discussion / Table Rond NADINE BEDNARZ 157 New Curriculum in Mathematics in Quebec: Continuities, Changes and Challenges / Nouveau curriculum d’études en mathématiques au Québec: Continuités et changements, questions qui se posent STEWART CRAVEN 165 Excerpts: The State of Mathematics Education in Ontario—Where We Came From and Where We Are in March, 2003 DONNA KARSTEN 171 Atlantic Canada Mathematics Curriculum and Nova Scotia Implementation TOM O’SHEA 175 Mathematics Curriculum in Canada Appendices 181 A • Working Groups at Each Annual Meeting 185 B • Plenary Lectures at Each Annual Meeting 189 C • Proceedings of Annual Meetings 191 D • List of Participants iv Acknowledgements On behalf of the members, the CMESG/GCEDM Executive would like to take this opportu- nity to thank our local hosts for their contributions to the 2003 Annual Meeting and Confer- ence. Specifically thank you to: David Reid, chair of the local organising committee; Jeff Hooper, treasurer; Debbie Boutilier, excursions; Sarah Perkins & Tony Wile, technical assis- tance, registrations, etc.; Richard Hoshino, transport; and Glen MacDuff, umbrellas. Supplementary materials to some of the contributions in these Proceedings are posted on the CMESG/GCEDM website (http://www.cmesg.math.ca), maintained by David Reid. The editors gratefully acknowledge the permission to reprint the following images and text: · The image of Napier’s Rods on page 45 is used by permission of the AIMS Education Foundation (Fresno, CA; http://www/aimseduorg; 1.888.733.2467). · The images in Appendices 1 & 2 of the Report of Working Group A (pp. 52–54) are re- printed with the permission of Dover, publishers of D.E. Smith’s The History of Mathemat- ics, Volume II. · The text on pages 76–77 is reprinted with the permission of Pbilosophy of Mathematics Edu- cation Journal (http://www.ex.ac.uk/~PErnest/pome11/art6htm). ·Simon’s Model of the Integrated Mathematics Teaching Cycle on page 126 is reprinted with the permission of Martin Simon. v Schedule Vendredi/ Samedi/ Dimanche/ Lundi/ Mardi/ Friday Saturday Sunday Monday Tuesday May 30 mai May 31 mai June 01 juin June 02 juin June 03 juin 1234567890123 1234567890123 1234567890123 1234567890123 1234567890123 1234567890123 1234567890123 1234567890123 1234567890123 9h00–11h00 1234567890123 1234567890123 Table rond/Panel 1234567890123 1234567890123 09h00–12h15 Discussion Matin/ 1234567890123 1234567890123 Groupes de travail / Working Groups 12345678901234 Morning1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 1234567890123 11h30–12h30 1234567890123 1234567890123 Séance de cloture/ 1234567890123 1234567890123 12345678901234Closing Session 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 12h15–13h45 12345678901234 1234567890123 12345678901234 1234567890123 Dîner / Lunch 12345678901234 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 12345678901234 1234567890123 13h45–14h30 13h45–14h45 13h45–14h30 12345678901234 1234567890123 12345678901234 1234567890123 Petits groupes/ Conférence 2/ Petits groupes/ 12345678901234 1234567890123 12345678901234 1234567890123 Small Groups Plenary 2: Small Groups 12345678901234 1234567890123 12345678901234 1234567890123 Sierpinska 12345678901234 1234567890123 14h30–15h30 14h30–15h30 12345678901234 1234567890123 14h45–15h45 12345678901234 Aprés- 1234567890123 Discussion de/of Discussion de/of 12345678901234 1234567890123 Archibald Groupes thématiques/ Sierpinska 12345678901234 midi/ 1234567890123123456789012345 12345678901234512345678901234 12345678901234123456789012345 Topic Groups 12345678901234152345678901234 After- 15h30–16h30 1234567890123415234567890123142345678901234152345678901234 noon 12345678901234512345678901231234567890123454 12345678901234 Registration/ 12345678901234 12345678901234 12345678901234 12345678901234 Inscription 16h00–17h00 12345678901234 12345678901234 Groupes thématiques/ 16h00–17h30 12345678901234 16h15–17h15 12345678901234 16h30–17h30 Topic Groups AGA / AGM 12345678901234 Ouverture/ New PhDs/Thèses 12345678901234 12345678901234 Opening Session 17h00–18h30 12345678901234 12345678901234 Teacher Workshops 12345678901234 12345678901234 ou/or Grand Pré 17h30–18h30 12345678901234 17h30–19h00 12345678901234 Grand Pré Ad Hocs 12345678901234 Souper/Supper 12345678901234 12345678901234 12345678901234 12345678901234 12345678901234 18h30–20h00 12345678901234 19h00–20h00 12345678901234 Soir/ Conférence 1/ Souper/Supper 12345678901234 12345678901234 Evening Plenary 1: 12345678901234 12345678901234 Archibald 12345678901234567890123456789012123456789012345678901234 12345678901234567890123456789012123456789102345678901234 12345678901234567890123456789012123456789102345678901234 12345678901234567890123456789012123456789102345678901234 20h00 12345678901234567890123456789012123456789102345678901234 12345678901234567890123456789012123456789102345678901234 Dessert & Social 12345678901234567890123456789012123456789102345678901234 12345678901234567890123456789012123456789102345678901234 12345678901234567890123456789012123456789012345678901234 vii Introduction Malgorzata Dubiel - President, CMESG/GCEDM Simon Fraser University It is my great pleasure to write an introduction to the CMESG/GCEDM Proceedings from the 2003 meeting, held at Acadia University in Wolfville, Nova Scotia. Alas, this volume cannot possibly convey the spirit of the meeting it reports on. It can merely describe the content of activities without giving much of the flavour of the process. Therefore, this introduction will attempt to tell you a little about our organization, and about our meetings. CMESG/GCDEM is unlike other professional organizations: One belongs to it not because of who one is professionally, but because of one’s interests. And that is why our members come from mathematics departments and faculties of education, from universi- ties and colleges, and from schools and other educational institutions. What unites them is an interest in mathematics and how it is taught at every level, and a desire to make teaching more exciting, more relevant, and more meaningful. Our meetings are unique, too. One does not simply attend a CMESG meeting the way one attends other professional meetings, by coming to listen to a few chosen talks. You are immediately part of it; you live and breathe it. And, even though the format, embedded in tradition, does not change much from year to year, there are
Load more

Recommended publications
  • Mathematics Is a Gentleman's Art: Analysis and Synthesis in American College Geometry Teaching, 1790-1840 Amy K
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 2000 Mathematics is a gentleman's art: Analysis and synthesis in American college geometry teaching, 1790-1840 Amy K. Ackerberg-Hastings Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Higher Education and Teaching Commons, History of Science, Technology, and Medicine Commons, and the Science and Mathematics Education Commons Recommended Citation Ackerberg-Hastings, Amy K., "Mathematics is a gentleman's art: Analysis and synthesis in American college geometry teaching, 1790-1840 " (2000). Retrospective Theses and Dissertations. 12669. https://lib.dr.iastate.edu/rtd/12669 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margwis, and improper alignment can adversely affect reproduction. in the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted.
    [Show full text]
  • BERMAN-THESIS-2020.Pdf (4.226Mb)
    The Attributes and Formation Mechanisms of Kallistos Vallis, Venus by Derek A. Berman, B.S. A Thesis In Geosciences Submitted to the Graduate Faculty of Texas Tech University in Partial Fulfillment of the Requirements for the Degree of MASTER OF SCIENCE Approved David W. Leverington, Ph.D. Chair of Committee Haraldur R. Karlsson, Ph.D. Harold Gurrola, Ph.D. Dr. Mark Sheridan Dean of the Graduate School December, 2020 Copyright 2020, Derek A. Berman Texas Tech University, Derek A. Berman, December 2020 ACKNOWLEDGMENTS I would like give my heartfelt gratitude and thanks to all my committee members. I would like to thank Dr. David Leverington for working with me these past years to accomplish this research and further my knowledge of planetary geology, geomorphology, and remote sensing. I hope this will be just the start to future collaborations, and that in 20 years we can still consider each other friends and colleagues in science. Thank you to Dr. Hal Karlsson for all your thoughtful comments and feedback on my thesis and a thank you to Dr. Harold Gurrola for serving on my thesis committee. I would also like to thank Lucia Barbato, Cameron Griffith, and Dr. Callum Hetherington for all the thoughtful advice, mentoring, and academic training. The three of you definitely helped to enrich my academic experience at TTU. The past several years have represented a huge personal growth period, full of challenges and triumphs. I want to thank all my friends and family members who lent me their undying support and motivation. I especially want to thank my sister Nicole, who was with me through the toughest of times, and my friends Giovanni, Luka, and Matteo, as well as all the members of the “Italian Club”, for your camaraderie and kind words of encouragement.
    [Show full text]
  • Rhyming Dictionary
    Merriam-Webster's Rhyming Dictionary Merriam-Webster, Incorporated Springfield, Massachusetts A GENUINE MERRIAM-WEBSTER The name Webster alone is no guarantee of excellence. It is used by a number of publishers and may serve mainly to mislead an unwary buyer. Merriam-Webster™ is the name you should look for when you consider the purchase of dictionaries or other fine reference books. It carries the reputation of a company that has been publishing since 1831 and is your assurance of quality and authority. Copyright © 2002 by Merriam-Webster, Incorporated Library of Congress Cataloging-in-Publication Data Merriam-Webster's rhyming dictionary, p. cm. ISBN 0-87779-632-7 1. English language-Rhyme-Dictionaries. I. Title: Rhyming dictionary. II. Merriam-Webster, Inc. PE1519 .M47 2002 423'.l-dc21 2001052192 All rights reserved. No part of this book covered by the copyrights hereon may be reproduced or copied in any form or by any means—graphic, electronic, or mechanical, including photocopying, taping, or information storage and retrieval systems—without written permission of the publisher. Printed and bound in the United States of America 234RRD/H05040302 Explanatory Notes MERRIAM-WEBSTER's RHYMING DICTIONARY is a listing of words grouped according to the way they rhyme. The words are drawn from Merriam- Webster's Collegiate Dictionary. Though many uncommon words can be found here, many highly technical or obscure words have been omitted, as have words whose only meanings are vulgar or offensive. Rhyming sound Words in this book are gathered into entries on the basis of their rhyming sound. The rhyming sound is the last part of the word, from the vowel sound in the last stressed syllable to the end of the word.
    [Show full text]
  • An Access-Dictionary of Internationalist High Tech Latinate English
    An Access-Dictionary of Internationalist High Tech Latinate English Excerpted from Word Power, Public Speaking Confidence, and Dictionary-Based Learning, Copyright © 2007 by Robert Oliphant, columnist, Education News Author of The Latin-Old English Glossary in British Museum MS 3376 (Mouton, 1966) and A Piano for Mrs. Cimino (Prentice Hall, 1980) INTRODUCTION Strictly speaking, this is simply a list of technical terms: 30,680 of them presented in an alphabetical sequence of 52 professional subject fields ranging from Aeronautics to Zoology. Practically considered, though, every item on the list can be quickly accessed in the Random House Webster’s Unabridged Dictionary (RHU), updated second edition of 2007, or in its CD – ROM WordGenius® version. So what’s here is actually an in-depth learning tool for mastering the basic vocabularies of what today can fairly be called American-Pronunciation Internationalist High Tech Latinate English. Dictionary authority. This list, by virtue of its dictionary link, has far more authority than a conventional professional-subject glossary, even the one offered online by the University of Maryland Medical Center. American dictionaries, after all, have always assigned their technical terms to professional experts in specific fields, identified those experts in print, and in effect held them responsible for the accuracy and comprehensiveness of each entry. Even more important, the entries themselves offer learners a complete sketch of each target word (headword). Memorization. For professionals, memorization is a basic career requirement. Any physician will tell you how much of it is called for in medical school and how hard it is, thanks to thousands of strange, exotic shapes like <myocardium> that have to be taken apart in the mind and reassembled like pieces of an unpronounceable jigsaw puzzle.
    [Show full text]
  • The Project Gutenberg Ebook #31061: a History of Mathematics
    The Project Gutenberg EBook of A History of Mathematics, by Florian Cajori This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: A History of Mathematics Author: Florian Cajori Release Date: January 24, 2010 [EBook #31061] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK A HISTORY OF MATHEMATICS *** Produced by Andrew D. Hwang, Peter Vachuska, Carl Hudkins and the Online Distributed Proofreading Team at http://www.pgdp.net transcriber's note Figures may have been moved with respect to the surrounding text. Minor typographical corrections and presentational changes have been made without comment. This PDF file is formatted for screen viewing, but may be easily formatted for printing. Please consult the preamble of the LATEX source file for instructions. A HISTORY OF MATHEMATICS A HISTORY OF MATHEMATICS BY FLORIAN CAJORI, Ph.D. Formerly Professor of Applied Mathematics in the Tulane University of Louisiana; now Professor of Physics in Colorado College \I am sure that no subject loses more than mathematics by any attempt to dissociate it from its history."|J. W. L. Glaisher New York THE MACMILLAN COMPANY LONDON: MACMILLAN & CO., Ltd. 1909 All rights reserved Copyright, 1893, By MACMILLAN AND CO. Set up and electrotyped January, 1894. Reprinted March, 1895; October, 1897; November, 1901; January, 1906; July, 1909. Norwood Pre&: J. S. Cushing & Co.|Berwick & Smith.
    [Show full text]
  • Sources and Studies in the History of Mathematics and Physical Sciences
    Sources and Studies in the History of Mathematics and Physical Sciences Editorial Board J.Z. Buchwald J. Lu¨tzen G.J. Toomer Advisory Board P.J. Davis T. Hawkins A.E. Shapiro D. Whiteside Gert Schubring Conflicts between Generalization, Rigor, and Intuition Number Concepts Underlying the Development of Analysis in 17–19th Century France and Germany With 21 Illustrations Gert Schubring Institut fu¨r Didaktik der Mathematik Universita¨t Bielefeld Universita¨tstraße 25 D-33615 Bielefeld Germany [email protected] Sources and Studies Editor: Jed Buchwald Division of the Humanities and Social Sciences 228-77 California Institute of Technology Pasadena, CA 91125 USA Library of Congress Cataloging-in-Publication Data Schubring, Gert. Conflicts between generalization, rigor, and intuition / Gert Schubring. p. cm. — (Sources and studies in the history of mathematics and physical sciences) Includes bibliographical references and index. ISBN 0-387-22836-5 (acid-free paper) 1. Mathematical analysis—History—18th century. 2. Mathematical analysis—History—19th century. 3. Numbers, Negative—History. 4. Calculus—History. I. Title. II. Series. QA300.S377 2005 515′.09—dc22 2004058918 ISBN-10: 0-387-22836-5 ISBN-13: 978-0387-22836-5 Printed on acid-free paper. © 2005 Springer Science+Business Media, Inc. All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, Inc., 233 Spring St., New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, com- puter software, or by similar or dissimilar methodology now known or hereafter developed is for- bidden.
    [Show full text]
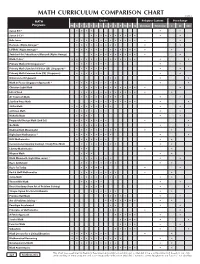
  • Math Curriculum Comparison Chart
    MATH CURRICULUM COMPARISON CHART ©2018 MATH Grades Religious Content Price Range Programs PK K 1 2 3 4 5 6 7 8 9 10 11 12 Christian N/Secular $ $$ $$$ Saxon K-3 * • • • • • • Saxon 3-12 * • • • • • • • • • • • • Bob Jones • • • • • • • • • • • • • • • Horizons (Alpha Omega) * • • • • • • • • • • • LIFEPAC (Alpha Omega) * • • • • • • • • • • • • • • • Switched-On Schoolhouse/Monarch (Alpha Omega) • • • • • • • • • • • • Math•U•See * • • • • • • • • • • • • • • • • Primary Math (US) (Singapore) * • • • • • • • • • Primary Math Standards Edition (SE) (Singapore) * • • • • • • • • • Primary Math Common Core (CC) (Singapore) • • • • • • • • Dimensions (Singapore) • • • • • Math in Focus (Singapore Approach) * • • • • • • • • • • • Christian Light Math • • • • • • • • • • • • • • Life of Fred • • • • • • • • • • • • • • A+ Tutorsoft Math • • • • • • • • • • • Starline Press Math • • • • • • • • • • • • ShillerMath • • • • • • • • • • • enVision Math • • • • • • • • • McRuffy Math • • • • • • Purposeful Design Math (2nd Ed.) • • • • • • • • • Go Math • • • • • • • • • Making Math Meaningful • • • • • • • • • • • RightStart Mathematics * • • • • • • • • • • MCP Mathematics • • • • • • • • • Conventional (Spunky Donkey) / Study Time Math • • • • • • • • • • Liberty Mathematics • • • • • Miquon Math • • • • • Math Mammoth (Light Blue series) * • • • • • • • • • Ray's Arithmetic • • • • • • • • • • Ray's for Today • • • • • • • Rod & Staff Mathematics • • • • • • • • • • Jump Math • • • • • • • • • • ThemeVille Math • • • • • • • Beast Academy (from
    [Show full text]
  • ILR Consolidated Table of Cases
    CONSOLIDATED TABLE OF CASES ARRANGED ALPHABETICALLY VOLUMES 1—125 Notes : This table of cases lists as comprehensively as possible, in alphabetical order, all cases reproduced or reported in the Annual Digest /International Law Reports, entering cases under all common variants of their title. It should be noted that many cases appearing in the AD/ILR do not have a title as such in their original version (e.g. in jurisdictions where the practice is to use case numbers rather than titles). There are other circumstances (e.g. ICJ cases) where to include the full formal title (including the introductory ‘Case concerning’) would be misleading in an alphabetical table. Such cases are listed under the key element[s] (e.g. ‘Aerial Incident of 27 July 1955’ rather than ‘Case concerning ...’). The full formal titles are used, where they exist, in the table of cases by jurisdiction. ILR practice, in the presentation of cases and in the treatment of cases referred to and in the matter of cross-references, has varied considerably over the years. So far as practicable, the current table brings earlier tables into conformity with current practice. Page references in earlier tables have accordingly been deleted where they contained no more than a cross- reference or a direction to another part of the volume where treatment of the case could be found. Where, in the Annual Digest in particular, a long extract from a case has been included, this has been treated as a full report rather than a note – ‘long’, of course, being a variable concept. Current ILR practice is, wherever appropriate, to use English in case titles (e.g.
    [Show full text]
  • Introduction: Venus, the Most Earth-Like Planet in Size and Mass
    id270364156 pdfMachine by Broadgun Software - a great PDF writer! - a great PDF creator! - http://www.pdfmachine.com http://www.broadgun.com Introduction: Venus, the most Earth-like planet in size and mass, experienced a very different history than Earth. Venus’ thick atmosphere of carbon dioxide, seventy times more dense than that of the Earth, hides her surface from optical view. Venus, an extremely dry planet, contains almost no water. Venus’ hot surface, approximately 750K, exhibits globally distributed volcanic and tectonic features, yet it records no evidence of plate tectonic processes and little evidence of extensive erosion. Instead of Earth’s linear belts, Venus hosts many circular to quasi-circular structures ranging from about 1 to 2600 km in diameter. The largest circular structures, approximately 1400 to 2600 km, consist of volcanic rises and crustal plateaus. Dome-like topographic swells define volcanic rises, whereas, steep-sided flat-topped structures characterize crustal plateaus (Phillips and Hansen, 1994; Smrekar et al., 1997). Other circular structures, chiefly impact craters and coronae, decorate the surface of Venus. Impact craters are circular depressions surrounded by a rim ranging from about 1.5 to 270 km in diameter caused by an exogenic process (Phillips et al., 1992, Schaber et al., 1992). A suite of approximately 515 circular to quasi-circular structures, called coronae, with diameters ranging from approximately 60 to 2600 km, overlap the range of diameters seen in volcanic rises, crustal plateaus, and impact craters (Stofan et al., 1992). Coronae, which are characterized by an annulus of fractures or ridges, variably display radial fractures, lava flows, and double ring structures (Barsukov et al., 1986; Basilevsky et al., 1986; Pronin and Stofan, 1 1990; Stofan et al., 1992; Stofan et al., 1997).
    [Show full text]
  • Geologic Map of the Agnesi Quadrangle (V–45), Venus
    Prepared for the National Aeronautics and Space Administration Geologic Map of the Agnesi Quadrangle (V–45), Venus By Vicki L. Hansen and Erik R. Tharalson Pamphlet to accompany Scientific Investigations Map 3250 75° 75° V–1 V–6 V–3 50° 50° V–7 V–2 V–17 V–10 V–18 V–9 V–19 V–8 25° 25° V–29 V–22 V–30 V–21 V–31 V–20 270° 300° 330° 0° 30° 60° 90° 0° 0° V–43 V–32 V–42 V–33 V–41 V–34 –25° –25° V–55 V–44 V–54 V–45 V–53 V–46 V–61 V–56 –50° –50° V–60 V–57 V–62 ° ° 2014 –75 –75 U.S. Department of the Interior U.S. Geological Survey Contents The Magellan Mission...................................................................................................................................1 Magellan Radar Data ...........................................................................................................................1 Agnesi Quadrangle ........................................................................................................................................1 Introduction............................................................................................................................................1 Data...... ..........................................................................................................................................2 Image Data ...........................................................................................................................2 Image Interpretation ..........................................................................................................2
    [Show full text]
  • Venus Geochemistry: Progress, Prospects, and New Missions, P
    V6NIA.SV6NIAS '160C 6MISTR.Y: 1>rOertss,1>roeress, 1>ros-ptl)ts,1>ros-ptots, A~ New Mtssto""-SMtsstoll\.S Program and Abstract Volume A LUNAR AND Y;~ PLANETARY ii;;; INSTITUTE LPI Contribution No. 1470 February 26–27, 2009 • Houston, Texas Sponsors Lunar and Planetary Institute NASA Science Mission Directorate NASA Mars Exploration Program Conveners Allan Treiman Lunar and Planetary Institute Adriana Ocampo NASA Science Mission Directorate Ellen Stofan Proxemy, VEXAG Stephen Mackwell Lunar and Planetary Institute Scientific Organizing Committee Allan Treiman Lunar and Planetary Institute Linda Elkins-Tanton Massachusetts Institute of Technology George Hashimoto Kobe University Natasha Johnson NASA Goddard Space Flight Center Eric Essene University of Michigan Stephen Mackwell Lunar and Planetary Institute Lunar and Planetary Institute 3600 Bay Area Boulevard Houston TX 77058-1113 LPI Contribution No. 1470 Compiled in 2009 by LUNAR AND PLANETARY INSTITUTE The Lunar and Planetary Institute is operated by the Universities Space Research Association under a cooperative agreement with the Science Mission Directorate of the National Aeronautics and Space Administration. Any opinions, findings, and conclusions or recommendations expressed in this volume are those of the author(s) and do not necessarily reflect the views of the National Aeronautics and Space Administration. Material in this volume may be copied without restraint for library, abstract service, education, or personal research purposes; however, republication of any paper or portion thereof requires the written permission of the authors as well as the appropriate acknowledgment of this publication. Abstracts in this volume may be cited as Author A. B. (2009) Title of abstract. In Workshop on Venus Geochemistry: Progress, Prospects, and New Missions, p.
    [Show full text]
  • 6 Polygonal Impact Craters (Pics) 18 6.1 Definition of Polygonal Impact Craters
    MASTERARBEIT Titel der Masterarbeit “Relative Age of Polygonal Impact Craters on Venus“ Verfasser Dipl.-Ing Gerhard Weihs BSc angestrebter akademischer Titel Master of Science (MSc) Wien, 2014 Studienkennzahl lt. Studienbuch: A 066 861 Studienrichtung lt. Studienblatt: Masterstudium Astronomie Betreuerin: Univ.-Prof. Dr. Maria G. Firneis Acknowledgement I gratefully acknowledge the thoughtful reviews by Univ.-Prof. Dr. Maria G. Firneis and Mag. Johannes J. Leitner, who significantly helped to improve the content and the style of this manuscript. Gerhard Weihs II Contents 1 Introduction 1 1.1 Aims of the Study . .1 1.2 Key Facts of Venus . .1 2 Venusian Surface 2 2.1 Geological Structures on Venusian Surface . .2 2.1.1 Main Elements of the Venusian Surface . .2 2.1.1.1 Volcanic Plains . .3 2.1.1.2 Intensely Deformed Terrains . .4 2.1.1.3 Coronae . .5 2.1.1.4 Impact Craters . .5 3 Geological History of the Venusian Surface 6 3.1 Short Overview of the Geological History . .6 3.2 Cratering Statistics . .7 3.3 Global Resurfacing of Venus . .8 3.3.1 Resurfacing Models . .8 3.3.2 Standard Model of Venusian Resurfacing . .9 4 Dating Planetary Surfaces 11 4.1 Methods of Dating Planetary Surfaces . 11 4.1.1 Absolute Dating - Chronology . 11 4.1.2 Relative Age Dating - Stratigraphy . 11 4.2 Chronology - Absolute Age Dating . 11 4.2.1 Using Radioactive Isotopes . 11 4.2.2 Using Crater Counting . 12 5 Impact Cratering Processes 15 5.1 The three Stages of Formation of Impact Craters . 15 5.1.1 Contact and Compression .
    [Show full text]