DOCSLIB.ORG

Sources and Studies in the History of Mathematics and Physical Sciences

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Sources and Studies in the History of Mathematics and Physical Sciences Sources and Studies in the History of Mathematics and Physical Sciences Editorial Board J.Z. Buchwald J. Lu¨tzen G.J. Toomer Advisory Board P.J. Davis T. Hawkins A.E. Shapiro D. Whiteside Gert Schubring Conflicts between Generalization, Rigor, and Intuition Number Concepts Underlying the Development of Analysis in 17–19th Century France and Germany With 21 Illustrations Gert Schubring Institut fu¨r Didaktik der Mathematik Universita¨t Bielefeld Universita¨tstraße 25 D-33615 Bielefeld Germany [email protected] Sources and Studies Editor: Jed Buchwald Division of the Humanities and Social Sciences 228-77 California Institute of Technology Pasadena, CA 91125 USA Library of Congress Cataloging-in-Publication Data Schubring, Gert. Conflicts between generalization, rigor, and intuition / Gert Schubring. p. cm. — (Sources and studies in the history of mathematics and physical sciences) Includes bibliographical references and index. ISBN 0-387-22836-5 (acid-free paper) 1. Mathematical analysis—History—18th century. 2. Mathematical analysis—History—19th century. 3. Numbers, Negative—History. 4. Calculus—History. I. Title. II. Series. QA300.S377 2005 515′.09—dc22 2004058918 ISBN-10: 0-387-22836-5 ISBN-13: 978-0387-22836-5 Printed on acid-free paper. © 2005 Springer Science+Business Media, Inc. All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, Inc., 233 Spring St., New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, com- puter software, or by similar or dissimilar methodology now known or hereafter developed is for- bidden. The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. Printed in the United States of America. (EB) 987654321 SPIN 10970683 springeronline.com Preface This volume is, as may be readily apparent, the fruit of many years’ labor in archives and libraries, unearthing rare books, researching Nachlässe, and above all, systematic comparative analysis of fecund sources. The work not only demanded much time in preparation, but was also interrupted by other duties, such as time spent as a guest professor at universities abroad, which of course provided welcome opportunities to present and discuss the work, and in particular, the organizing of the 1994 International Graßmann Conference and the subsequent editing of its proceedings. If it is not possible to be precise about the amount of time spent on this work, it is possible to be precise about the date of its inception. In 1984, during research in the archive of the École polytechnique, my attention was drawn to the way in which the massive rupture that took place in 1811—precipitating the change back to the synthetic method and replacing the limit method by the method of the quantités infiniment petites—significantly altered the teaching of analysis at this first modern institution of higher education, an institution originally founded as a citadel of the analytic method. And it was in a French context, so favorably disposed to establishing links between history and epistemology, that I first presented my view that concept development is culturally shaped; it was at the third Ecole d'Eté de Didactique des Mathéma- tiques of July 1984 in Orléans that I presented my paper “Le retour du réfoulé— Les débats sur ‘La Méthode’ à la fin du 18ème et au debut du 19ème siècle: Condillac, Lacroix et les successeurs.” When the work was eventually completed in 2002, it was accepted as a Habilitationsschrift by the Mathematics Department of the University of Bielefeld. I am grateful to Jesper Lützen, editor of the series Sources and Studies in the History of Mathematics and Physical Sciences, and to the publishing house of Springer, for publishing the script in their series. The relatively independent former Chapter C, investigating the context of the 1811 switch in the basic conceptions at the École polytechnique is published separately as “Le Retour du Réfoulé—Der Wiederaufstieg der synthetischen Methode an der École polytechnique” (Augsburg: Rauner, 2004). Its principal results are summarized here in Chapter IV.3. VI Preface In an effort to accelerate the publication of this volume, the sheer size of the manuscript led me to organize its translation from German into English, practically as a collective endeavor. I am indebted to the commitment shown by Jonathan Harrow and Günter Seib, Chris Weeks, and Dorit Funke as translators. I wish to thank the following archives for their kind permission to reproduce documents: Archiv der Berlin–Brandenburgischen Akademie der Wissenschaften (Berlin), Archives de l’École polytechnique (Paris/Palaiseau), Archives de l’Académie des Sciences (Paris). In conclusion, I should like to make two points. Firstly, all the translations of non-English quotations—both from the original sources and from publications— are ours, except in cases where English translations already existed, which are so indicated. In a few cases, the original quotation is preserved when the context makes its meaning sufficiently clear. The second point concerns terminology. The French reflections on foundations constitute the major focus of this study; consequently, the “triad” of basic concepts used in French mathematics to “span” the contemporary concept fields—namely quantité, grandeur, and nombre—is also used here, as the configuration of basic terms. Since quantité was understood to be the key foundational concept (cf. the Encyclopédie defining mathematics as the science of quantité), and since my English terms are intended to recall the French understanding of the time, quantité is rendered here throughout as “quantity,” and grandeur as “magnitude.” University of Bielefeld Gert Schubring September 2004 Contents Preface v Illustrations xiv I. Question and Method 1 1. Methodological Approaches to the History of Science 1 2. Categories for the Analysis of Culturally Shaped Conceptual Developments 8 3. An unusual Pair: Negative Numbers and Infinitely Small Quantities 10 II. Paths Toward Algebraization – Development to the Eighteenth Century. The Number Field 15 1. An Overview of the History of Key Fundamental Concepts 15 1.1. The Concept of Number 16 1.2. The Concept of Variable 19 1.3. The Concept of Function 20 1.4. The Concept of Limit 22 1.5. Continuity 25 1.6. Convergence 27 1.7. The Integral 30 2. The Development of Negative Numbers 32 2.1. Introduction 32 2.2 An Overview of the Early History of Negative Numbers 35 From Antiquity to the Middle Ages 35 European Mathematics in the Middle Ages 39 2.3. The Onset of Early Modern Times. The First “Ruptures” in Cardano’s Works 40 2.4. Further Developments in Algebra: From Viète to Descartes 45 VIII Contents 2.5. The Controversy Between Arnauld and Prestet 49 A New Type of Textbook 49 Antoine Arnauld 50 Jean Prestet 52 The Controversy 54 The Debate’s Effects on Their Textbook Reeditions 57 2.6. An Insertion: Brief Comparison of the Institutions for Mathematical Teaching in France, Germany, and England 61 Universities and Faculties of Arts and Philosophy 61 The Status of Mathematics in Various Systems of National Education 64 New Approaches in the Eighteenth Century 66 2.7. First Foundational Reflections on Generalization 67 2.8. Extension of the Concept Field to 1730/40 73 2.8.1. France 73 2.8.2. Developments in England and Scotland 88 2.8.3. The Beginnings in Germany 95 2.9. The Onset of an Epistemological Rupture 99 2.9.1. Fontenelle: Separation of Quantity from Quality 99 2.9.2. Clairaut: Reinterpreting the Negative as Positive 102 2.9.3. D’Alembert: The Generality of Algebra—An Inconvénient 104 2.10. Aspects of the Crisis to 1800 114 2.10.1. Stagnant Waters in the French University Context 114 2.10.2. The Military Schools as Multipliers 121 2.10.3. Violent Reaction in England and Scotland 126 2.10.4. The Concept of Oppositeness in Germany 132 2.11. Looking Back 149 III. Paths toward Algebraization—The Field of Limits: The Development of Infinitely Small Quantities 151 1. Introduction 151 2. From Antiquity to Modern Times 153 Concepts of the Greek Philosophers 154 3. Early Modern Times 157 Contents IX 4. The Founders of Infinitesimal Calculus 161 5. The Law of Continuity: Law of Nature or Mathematical Abstraction? 174 6. The Concept of Infinitely Small Quantities Emerges 186 7. Consolidating the Concept of Infinitely Small Quantities 192 8. The Elaboration of the Concept of Limit 206 8.1. Limits as MacLaurin’s Answer to Berkeley 206 8.2. Reception in the Encyclopédie and Its Dissemination 209 8.3. A Muddling of Uses in French University Textbooks 213 8.4. First Explications of the Limit Approach 220 8.5. Expansion of the Limit Approach and Beginnings of Its Algebraization 228 9. Operationalizations of the Concept of Continuity 238 10. A Survey 255 IV. Culmination of Algebraization and Retour du Refoulé 257 1. The Number Field: Additional Approaches Toward Algebraization in Europe and Countercurrents 257 1.1. Euler: The Basis of Mathematics is Numbers, not Quantities 257 1.2. Condillac: Genetic Reconstruction of the Extension of the Number Field 260 1.3. Buée: Application of Algebra as a Language 265 1.4. Fundamentalist Countercurrents 268 Klostermann: Elementary Geometry versus Algebra 276 2. The Limit Field: Dominance of the Analytic Method in France After 1789 279 2.1. Apotheosis of the Analytic Method 279 2.2. Euler’s Reception 283 2.3. Algebraic Approaches at the École Polytechnique 286 3. Le Retour du Refoulé: The Renaissance of the Synthetic Method at the École Polytechnique 295 3.1.
Load more

Recommended publications
  • Arxiv:1812.00226V2 [Math.HO] 11 Feb 2019 2010 EBI’ ELFUDDFCIN N THEIR and FICTIONS WELL-FOUNDED LEIBNIZ’S ..Bso W Prahs5 Approaches Two on Bos 130 1.2
    LEIBNIZ’S WELL-FOUNDED FICTIONS AND THEIR INTERPRETATIONS JACQUES BAIR, PIOTR BLASZCZYK, ROBERT ELY, PETER HEINIG, AND MIKHAIL G. KATZ Abstract. Leibniz used the term fiction in conjunction with in- finitesimals. What kind of fictions they were exactly is a subject of scholarly dispute. The position of Bos and Mancosu contrasts with that of Ishiguro and Arthur. Leibniz’s own views, expressed in his published articles and correspondence, led Bos to distinguish between two methods in Leibniz’s work: (A) one exploiting clas- sical ‘exhaustion’ arguments, and (B) one exploiting inassignable infinitesimals together with a law of continuity. Of particular interest is evidence stemming from Leibniz’s work Nouveaux Essais sur l’Entendement Humain as well as from his correspondence with Arnauld, Bignon, Dagincourt, Des Bosses, and Varignon. A careful examination of the evidence leads us to the opposite conclusion from Arthur’s. We analyze a hitherto unnoticed objection of Rolle’s concern- ing the lack of justification for extending axioms and operations in geometry and analysis from the ordinary domain to that of infini- tesimal calculus, and reactions to it by Saurin and Leibniz. A newly released 1705 manuscript by Leibniz (Puisque des per- sonnes. ) currently in the process of digitalisation, sheds light on the nature of Leibnizian inassignable infinitesimals. In a pair of 1695 texts Leibniz made it clear that his incompa- rable magnitudes violate Euclid’s Definition V.4, a.k.a. the Archi- medean property, corroborating the non-Archimedean construal of the Leibnizian calculus. Keywords: Archimedean property; assignable vs inassignable quantity; Euclid’s Definition V.4; infinitesimal; law of continuity; arXiv:1812.00226v2 [math.HO] 11 Feb 2019 law of homogeneity; logical fiction; Nouveaux Essais; pure fiction; quantifier-assisted paraphrase; syncategorematic; transfer princi- ple; Arnauld; Bignon; Des Bosses; Rolle; Saurin; Varignon Contents 1.
    [Show full text]
  • Mathematics Is a Gentleman's Art: Analysis and Synthesis in American College Geometry Teaching, 1790-1840 Amy K
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 2000 Mathematics is a gentleman's art: Analysis and synthesis in American college geometry teaching, 1790-1840 Amy K. Ackerberg-Hastings Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Higher Education and Teaching Commons, History of Science, Technology, and Medicine Commons, and the Science and Mathematics Education Commons Recommended Citation Ackerberg-Hastings, Amy K., "Mathematics is a gentleman's art: Analysis and synthesis in American college geometry teaching, 1790-1840 " (2000). Retrospective Theses and Dissertations. 12669. https://lib.dr.iastate.edu/rtd/12669 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margwis, and improper alignment can adversely affect reproduction. in the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted.
    [Show full text]
  • BERMAN-THESIS-2020.Pdf (4.226Mb)
    The Attributes and Formation Mechanisms of Kallistos Vallis, Venus by Derek A. Berman, B.S. A Thesis In Geosciences Submitted to the Graduate Faculty of Texas Tech University in Partial Fulfillment of the Requirements for the Degree of MASTER OF SCIENCE Approved David W. Leverington, Ph.D. Chair of Committee Haraldur R. Karlsson, Ph.D. Harold Gurrola, Ph.D. Dr. Mark Sheridan Dean of the Graduate School December, 2020 Copyright 2020, Derek A. Berman Texas Tech University, Derek A. Berman, December 2020 ACKNOWLEDGMENTS I would like give my heartfelt gratitude and thanks to all my committee members. I would like to thank Dr. David Leverington for working with me these past years to accomplish this research and further my knowledge of planetary geology, geomorphology, and remote sensing. I hope this will be just the start to future collaborations, and that in 20 years we can still consider each other friends and colleagues in science. Thank you to Dr. Hal Karlsson for all your thoughtful comments and feedback on my thesis and a thank you to Dr. Harold Gurrola for serving on my thesis committee. I would also like to thank Lucia Barbato, Cameron Griffith, and Dr. Callum Hetherington for all the thoughtful advice, mentoring, and academic training. The three of you definitely helped to enrich my academic experience at TTU. The past several years have represented a huge personal growth period, full of challenges and triumphs. I want to thank all my friends and family members who lent me their undying support and motivation. I especially want to thank my sister Nicole, who was with me through the toughest of times, and my friends Giovanni, Luka, and Matteo, as well as all the members of the “Italian Club”, for your camaraderie and kind words of encouragement.
    [Show full text]
  • Hermeneutics of the Differential Calculus in Eighteenth- Century Europe
    Hermeneutics of the differential calculus in eighteenth- century Europe: from the Analyse des infiniment petits by L’Hôpital (1696) to the Traité élémentaire de calcul différentiel et de calcul intégral by Lacroix (1802)12 Mónica Blanco Abellán Departament de Matemàtica Aplicada III Universitat Politècnica de Catalunya In the history of mathematics it has not been unusual to assume that the communication of mathematical knowledge among countries flowed without constraints, partly because mathematics has often been considered as “universal knowledge”. Schubring,3 however, does not agree with this view and prefers referring to the basic units of communication, which enable the common understanding of knowledge. The basic unit should be constituted by a common language and a common culture, both interacting within a common national or state context. Insofar this interaction occurs within a national educational system, communication is here potentially possible. Consequently Schubring proposes comparative analysis of textbooks as a means to examine the differences between countries with regard to style, meaning and epistemology, since they emerge from a specific educational context. Taking Schubring’s views as starting point, the aim of this paper is to analyze and compare the mathematical development of the differential calculus in France, Germany, Italy and Britain through a number of specific works on the subject, and within their corresponding educational systems. The paper opens with an outline of the institutional framework of mathematical education in these countries. In order to assess the mathematical development of the works to be analyzed, the paper proceeds with a sketch of the epistelomogical aspects of the differential calculus in the eighteenth century.
    [Show full text]
  • Rhyming Dictionary
    Merriam-Webster's Rhyming Dictionary Merriam-Webster, Incorporated Springfield, Massachusetts A GENUINE MERRIAM-WEBSTER The name Webster alone is no guarantee of excellence. It is used by a number of publishers and may serve mainly to mislead an unwary buyer. Merriam-Webster™ is the name you should look for when you consider the purchase of dictionaries or other fine reference books. It carries the reputation of a company that has been publishing since 1831 and is your assurance of quality and authority. Copyright © 2002 by Merriam-Webster, Incorporated Library of Congress Cataloging-in-Publication Data Merriam-Webster's rhyming dictionary, p. cm. ISBN 0-87779-632-7 1. English language-Rhyme-Dictionaries. I. Title: Rhyming dictionary. II. Merriam-Webster, Inc. PE1519 .M47 2002 423'.l-dc21 2001052192 All rights reserved. No part of this book covered by the copyrights hereon may be reproduced or copied in any form or by any means—graphic, electronic, or mechanical, including photocopying, taping, or information storage and retrieval systems—without written permission of the publisher. Printed and bound in the United States of America 234RRD/H05040302 Explanatory Notes MERRIAM-WEBSTER's RHYMING DICTIONARY is a listing of words grouped according to the way they rhyme. The words are drawn from Merriam- Webster's Collegiate Dictionary. Though many uncommon words can be found here, many highly technical or obscure words have been omitted, as have words whose only meanings are vulgar or offensive. Rhyming sound Words in this book are gathered into entries on the basis of their rhyming sound. The rhyming sound is the last part of the word, from the vowel sound in the last stressed syllable to the end of the word.
    [Show full text]
  • An Access-Dictionary of Internationalist High Tech Latinate English
    An Access-Dictionary of Internationalist High Tech Latinate English Excerpted from Word Power, Public Speaking Confidence, and Dictionary-Based Learning, Copyright © 2007 by Robert Oliphant, columnist, Education News Author of The Latin-Old English Glossary in British Museum MS 3376 (Mouton, 1966) and A Piano for Mrs. Cimino (Prentice Hall, 1980) INTRODUCTION Strictly speaking, this is simply a list of technical terms: 30,680 of them presented in an alphabetical sequence of 52 professional subject fields ranging from Aeronautics to Zoology. Practically considered, though, every item on the list can be quickly accessed in the Random House Webster’s Unabridged Dictionary (RHU), updated second edition of 2007, or in its CD – ROM WordGenius® version. So what’s here is actually an in-depth learning tool for mastering the basic vocabularies of what today can fairly be called American-Pronunciation Internationalist High Tech Latinate English. Dictionary authority. This list, by virtue of its dictionary link, has far more authority than a conventional professional-subject glossary, even the one offered online by the University of Maryland Medical Center. American dictionaries, after all, have always assigned their technical terms to professional experts in specific fields, identified those experts in print, and in effect held them responsible for the accuracy and comprehensiveness of each entry. Even more important, the entries themselves offer learners a complete sketch of each target word (headword). Memorization. For professionals, memorization is a basic career requirement. Any physician will tell you how much of it is called for in medical school and how hard it is, thanks to thousands of strange, exotic shapes like <myocardium> that have to be taken apart in the mind and reassembled like pieces of an unpronounceable jigsaw puzzle.
    [Show full text]
  • The Project Gutenberg Ebook #31061: a History of Mathematics
    The Project Gutenberg EBook of A History of Mathematics, by Florian Cajori This eBook is for the use of anyone anywhere at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org Title: A History of Mathematics Author: Florian Cajori Release Date: January 24, 2010 [EBook #31061] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK A HISTORY OF MATHEMATICS *** Produced by Andrew D. Hwang, Peter Vachuska, Carl Hudkins and the Online Distributed Proofreading Team at http://www.pgdp.net transcriber's note Figures may have been moved with respect to the surrounding text. Minor typographical corrections and presentational changes have been made without comment. This PDF file is formatted for screen viewing, but may be easily formatted for printing. Please consult the preamble of the LATEX source file for instructions. A HISTORY OF MATHEMATICS A HISTORY OF MATHEMATICS BY FLORIAN CAJORI, Ph.D. Formerly Professor of Applied Mathematics in the Tulane University of Louisiana; now Professor of Physics in Colorado College \I am sure that no subject loses more than mathematics by any attempt to dissociate it from its history."|J. W. L. Glaisher New York THE MACMILLAN COMPANY LONDON: MACMILLAN & CO., Ltd. 1909 All rights reserved Copyright, 1893, By MACMILLAN AND CO. Set up and electrotyped January, 1894. Reprinted March, 1895; October, 1897; November, 1901; January, 1906; July, 1909. Norwood Pre&: J. S. Cushing & Co.|Berwick & Smith.
    [Show full text]
  • Berkeley Bibliography
    Berkeley Bibliography (1979-2019) Abad, Juan Vázques. “Observaciones sobre la noción de causa en el opusculo sobre el movimiento de Berkeley.” Analisis Filosofico 6 (1986): 35-44. Abelove, H. “George Berkeley’s Attitude to John Wesley: the Evidence of a Lost Letter.” Harvard Theological Review 70 (1977): 175-76. Ablondi, Fred. “Berkeley, Archetypes, and Errors.” Southern Journal of Philosophy 43 (2005): 493- 504. _____. “Absolute Beginners: Learning Philosophy by Learning Descartes and Berkeley.” Metascience 19 (2010): 385-89. _____. “On the Ghosts of Departed Quantities.” Metascience 21 (2012): 681-83. _____. “Hutcheson, Perception, and the Sceptic’s Challenge.” British Journal for the History of Philosophy 20 (2012): 269-81. Ackel, Helen. Über den Prozess der menschlichen Erkenntnis bei John Locke und George Berkeley. München und Ravensburg: Grin, 2008. Adamczykowa, Izabella. “The Role of the Subject in the Cognitive Process after George Berkeley: Passive for Active Subject?” Annales Universitatis Mariae Curie Sklodowska, Sectio 1 Philosophia-Sociologia 6 (1981): 43-57. Adar, Einat. “From Irish Philosophy to Irish Theatre: The Blind (Wo)Man Made to See.” Estudios Irlandeses 12 (2017): 1-11. Addyman, David and Feldman, Matthew. “Samuel Beckett, Wilhelm Windelband, and the Interwar ‘Philosophy Notes’.” Modernism/Modernity 18 (2011): 755-70. Agassi, Joseph. “The Future of Berkeley’s Instrumentalism.” International Studies in Philosophy 7 (1975), 167-78. Aichele, Alexander. “Ich Denke Was, Was Du Nicht Denkst, Und Das Ist Rot. John Locke Und George Berkeley Über Abstrakte Ideen Und Kants Logischer Abstraktionismus.” Kant- Studien 103 (2012): 25-46. Airaksinen, Timo. “Berkeley and the Justification of Beliefs [Abstract].” Berkeley Newsletter 8 (1985), 9.
    [Show full text]
  • History of Calculus
    History of Calculus Let’s start with the definition of mathematics and calculus. Mathematics – from the Greek knowledge, study learning. Is the study of quantity, structure, space and change. Calculus (Latin, calculus, a small stone used for counting) is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. Is the mathematics of instantaneous rates of change – how rapidly is some particular quantity changing at this very instant? Calculus has two main branches. Differential calculus provides methods for calculating rates of change and it has many geometric applications, in particular finding tangents to curves. Integral calculus does the opposite: give the rates of chance of some quantity, it specifies the quantity itself. Geometric applications of integral calculus include the computation of areas and volumes. Perhaps the most significant is this unexpected connection between two apparently unrelated classical geometric questions: finding tangents to a curve and finding areas. Why do we have to learn mathematics? Where mathematics came from? Mathematics came from our imagination; it is a complete invention of the human brain. With the invention of mathematics we create science. Mathematics makes up human, because it’s a distinction that we have from all others animals in the animal’s kingdom. The important of mathematics and science is so great that no person living in the twentieth century can claim to be educated if they are unaware of the modern vision of the physical universe and the history of the magnificent concepts that it embodies. Science is not rigid. Dogmas are rigid. We should understand that science is the business of measuring things.
    [Show full text]
  • Gallois Galois
    GALLOIS GALOIS Individual works include Grundzfige der schlesischen geometer with Michel Rolle and Pierre Varignon . He Klinratologie (Breslau, 1857); Uher die Verbesserung der stated his intention of publishing a critical translation Plan eten elem en te (Breslau, 1858) ; Uber eine Bestimmung of Pappus, but nothing came of this project . Instead, der Sonnenparallaxe arts korrespondierenden Beohachtungen he stimulated the quarrel between his two colleagues des Planeten Flora (Breslau, 1875) ; and Mitteilungen der concerning differential calculus and impeded its set- Koniglichen Universitdts-Stern warte Breslau fiber hier hisher tlement until 1706 . gewonnene Resultate fur die geographischen and klimato- Despite this negative attitude, the consequences of logischen Ortsverhdltnisse (Breslau, 1879). If . SECONDARY LITERATURE . Works on Galle and his which might have been disastrous, Gallois deserves work are W . Foerster, "J . G. Galle," in Vierteljahrsschrift recognition by historians of science for his activities der Astronornischen Gesellschaft, 46 (1911), 17-22 ; and D . as a publicist. Although he wrote somewhat fancifully Wattenberg, J. G. Galle (Leipzig, 1963). and with little concern for coherence, he was of H . C . FREILSLEBEN service in his time as a disseminator of ideas and his work is still valuable as an historical source . GALLOIS, JEAN (b. Paris, France, 11 June 1632 ; d. Paris, 19 April 1707), history of science. The son of a counsel to the Parlement of Paris, BIBLIOGRAPHY Gallois seems to have distinguished himself in that city around 1664 by the breadth of his learning, I . ORIGINAL WORKS . Gallois's translations and other works include Traduction latine du traite de paix des by his knowledge of Hebrew and of both living and Pyrenees (Paris, 1659) ; Breviannn Colhertinum (Paris, classical languages, by his interest in the sciences, and 1679) : "Extrait du livre intitule : Observations physiques et by a genuine literary talent .
    [Show full text]
  • A Calendar of Mathematical Dates January
    A CALENDAR OF MATHEMATICAL DATES V. Frederick Rickey Department of Mathematical Sciences United States Military Academy West Point, NY 10996-1786 USA Email: fred-rickey @ usma.edu JANUARY 1 January 4713 B.C. This is Julian day 1 and begins at noon Greenwich or Universal Time (U.T.). It provides a convenient way to keep track of the number of days between events. Noon, January 1, 1984, begins Julian Day 2,445,336. For the use of the Chinese remainder theorem in determining this date, see American Journal of Physics, 49(1981), 658{661. 46 B.C. The first day of the first year of the Julian calendar. It remained in effect until October 4, 1582. The previous year, \the last year of confusion," was the longest year on record|it contained 445 days. [Encyclopedia Brittanica, 13th edition, vol. 4, p. 990] 1618 La Salle's expedition reached the present site of Peoria, Illinois, birthplace of the author of this calendar. 1800 Cauchy's father was elected Secretary of the Senate in France. The young Cauchy used a corner of his father's office in Luxembourg Palace for his own desk. LaGrange and Laplace frequently stopped in on business and so took an interest in the boys mathematical talent. One day, in the presence of numerous dignitaries, Lagrange pointed to the young Cauchy and said \You see that little young man? Well! He will supplant all of us in so far as we are mathematicians." [E. T. Bell, Men of Mathematics, p. 274] 1801 Giuseppe Piazzi (1746{1826) discovered the first asteroid, Ceres, but lost it in the sun 41 days later, after only a few observations.
    [Show full text]
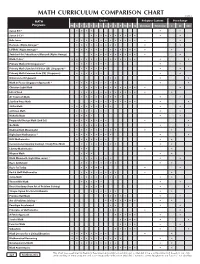
  • Math Curriculum Comparison Chart
    MATH CURRICULUM COMPARISON CHART ©2018 MATH Grades Religious Content Price Range Programs PK K 1 2 3 4 5 6 7 8 9 10 11 12 Christian N/Secular $ $$ $$$ Saxon K-3 * • • • • • • Saxon 3-12 * • • • • • • • • • • • • Bob Jones • • • • • • • • • • • • • • • Horizons (Alpha Omega) * • • • • • • • • • • • LIFEPAC (Alpha Omega) * • • • • • • • • • • • • • • • Switched-On Schoolhouse/Monarch (Alpha Omega) • • • • • • • • • • • • Math•U•See * • • • • • • • • • • • • • • • • Primary Math (US) (Singapore) * • • • • • • • • • Primary Math Standards Edition (SE) (Singapore) * • • • • • • • • • Primary Math Common Core (CC) (Singapore) • • • • • • • • Dimensions (Singapore) • • • • • Math in Focus (Singapore Approach) * • • • • • • • • • • • Christian Light Math • • • • • • • • • • • • • • Life of Fred • • • • • • • • • • • • • • A+ Tutorsoft Math • • • • • • • • • • • Starline Press Math • • • • • • • • • • • • ShillerMath • • • • • • • • • • • enVision Math • • • • • • • • • McRuffy Math • • • • • • Purposeful Design Math (2nd Ed.) • • • • • • • • • Go Math • • • • • • • • • Making Math Meaningful • • • • • • • • • • • RightStart Mathematics * • • • • • • • • • • MCP Mathematics • • • • • • • • • Conventional (Spunky Donkey) / Study Time Math • • • • • • • • • • Liberty Mathematics • • • • • Miquon Math • • • • • Math Mammoth (Light Blue series) * • • • • • • • • • Ray's Arithmetic • • • • • • • • • • Ray's for Today • • • • • • • Rod & Staff Mathematics • • • • • • • • • • Jump Math • • • • • • • • • • ThemeVille Math • • • • • • • Beast Academy (from
    [Show full text]