DOCSLIB.ORG

Riemannian Geometry

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Riemannian Geometry Riemannian Geometry Contents Chapter 1. Smooth manifolds 5 1. Tangent vectors, cotangent vectors and tensors 5 2. The tangent bundle of a smooth manifold 5 3. Vector fields, covector fields, tensor fields, n-forms 5 Chapter 2. Riemannian manifolds 7 1. Riemannian metric 7 2. The three model geometries 9 3. Connections 13 4. Geodesics and parallel translation along curves 16 5. The Riemannian connection 17 6. Connections on submanifolds and pull-back connections 19 7. Geodesics in the three geometries 20 8. The exponential map and normal coordinates 21 9. The Riemann distance function 25 Chapter 3. Curvature 29 1. The Riemann curvature tensor 29 2. Ricci curvature, scalar curvature, and Einstein metrics 31 3. Riemannian submanifolds 33 4. Sectional curvature 36 5. Jacobi fields 38 6. Comparison theorems 44 Chapter 4. Space-times 47 Chapter 5. Multilinear Algebra 49 1. Tensors 49 2. Tensors of inner product spaces 51 3. Coordinate expressions 52 Chapter 6. Non-euclidean geometry 55 1. The hyperbolic plane 55 Bibliography 59 3 CHAPTER 1 Smooth manifolds 1. Tangent vectors, cotangent vectors and tensors 1.1. Lemma. Let F : M m → N n be a smooth map. Suppose that (x1, . , xm) are local co- ordinates on M and (y1, . , yn) local coordinates on N. Then ∂ ∂(yiF ) ∂ (1.2) F∗( ∂xj ) = ∂xj ∂yi , 1 ≤ j ≤ m, ∗ i ∂(yiF ) j i (1.3) F (dy ) = ∂xj dx = d(y F ), 1 ≤ i ≤ n t ∂(yiF ) ∂(yiF ) The (n × m)-matrix ∂xj is the matrix for F∗ and the (m × n)-matrix ∂xj is the matrix for F ∗. In other words, ∂ ∂ ∂ ∂ ∂(yiF ) F∗ ∂x1 ...F∗ ∂xm = ∂y1 ... ∂yn ∂xj F ∗dy1 dx1 i . = ∂(y F ) . . ∂xj . F ∗dyn dxm ∗ i ∂ i ∂ ∂ i ∂yiF Proof. F (dy )( ∂xj ) = dy (F∗( ∂xj )) = F∗ ∂xj (y ) = ∂xj . 2. The tangent bundle of a smooth manifold 3. Vector fields, covector fields, tensor fields, n-forms 1.4. Proposition. The differential d: C∞(M) → T 1(M) is an R-linear map satisfying the derivational rules du udv vdu − udv d(uv) = (du)v + u(dv), d u = − = v v v2 v2 for all smooth functions u, v ∈ C∞(M) (where v(p) 6= 0 for all p ∈ M in the last formula). If F : M → N is a smooth map, then the diagram F ∗ C∞(M) o C∞(N) d d F ∗ T 1(M) o T 1(N) commutes meaning that F ∗(du) = d(uF ) for all u ∈ C∞(N). n+1 2 Pn+1 i 2 1.5. Example. Let s: R → R be the smooth map s(x) = |x| = i=1 (x ) . Then s−1(1) = Sn ⊂ Rn is the sphere of radius R. The differential ds = P 2xidxi is the linear n+1 n+1 P i i ⊥ map R = TpR → R given by dsp(v) = 2p v = 2hp, vi with kernel ker dsp = p at any n n n+1 n+1 point p 6= 0. Let p be any point of S and ι∗ : TpS → TpR = R the linear map induced n by the inclusion, ι. For any tangent vector X ∈ TpS , ds(ι∗X) = X(sι) = X(1) = 0. Hence the tangent space at p is the kernel of dsp, n ⊥ n+1 n+1 TpS = p ⊂ R = TpR and the tangent bundle of Sn, TSn = {(p, v) ⊂ Sn × Rn+1 | hv, pi = 0} ⊂ Sn × Rn+1 5 6 1. SMOOTH manifoldS is the vector bundle whose fibre over any p ∈ Sn is p⊥. A smooth vector field on Sn is a smooth map v : Sn → Rn+1 such that v(p) ⊥ p for all p ∈ Sn. Show that any odd sphere has a vector field without zeros. Does S2 admit a smooth vector field with no zeros? Can you describe T RP n? Can you describe TM if M = f −1(0) consists of the manifold solutions to the equation f(x) = 0 for some smooth map f : Rn+1 → R? k 1.6. Definition. A smooth -tensor field on M is a smooth section of the tensor bundle ` k T` (M) → M. Particular cases are 0 ∞ •T0 (M) = C (M) 0 •T1 (M) consists of vector fields on M 1 •T0 (M) consists of 1-forms on M Tensor fields admit ⊗ •T k1 (M) × T k1 (M) −→T k1+k2 (M) (tensor product of tensor fields) `1 `1 `1+`2 k+1 tr k •T`+1 (M) −→T` (M) (contraction of tensor fields) 1 0 1.7. Example. Let ω ∈ T0 (M) be a 1-form and X ∈ T1 (M) a vector field on M. Then 1 X ⊗ ω ∈ T 1(M) is -tensor field with contraction tr(X ⊗ ω) = ω(X) (5.7). 1 1 k In a coordinate patch any -tensor field A is (5.5) a C∞(M)-linear combination ` (1.8) A = Aj1···j` ∂ ⊗ · · · ∂ ⊗ dxi1 ⊗ · · · dxik i1···ik j1 j` of tensor products of the basis tensor fields and basis 1-forms. The smooth functions Aj1···j` are i1···ik called the components of the tensor field A. ∗ P∞ k The tensor algebra of M is the graded algebra T (M) = k=0 T (M) equipped with the tensor product T r(M) × T s(M) −→T⊗ r+s(M). If F : M → N is a smooth map, F ∗ : T k(N) → T k(M) ∗ k is the linear map given by F (A)(X1,...,Xk) = A(F∗X1,...,F∗Xk) for all A ∈ T (N) and all smooth vector fields X1,...,Xk on M. 1.9. Lemma. T ∗(M) is a graded algebra. F ∗ : T ∗(N) → T ∗(M) is a homomorphism of C∞(N)- algebras: F ∗(aω ⊗ η) = F ∗(a)F ∗(ω) ⊗ F ∗(η). CHAPTER 2 Riemannian manifolds Riemann’s idea was that in the infinitely small, on a scale much smaller than the the smallest particle, we do not know if Euclidean geometry is still in force. Therefore we better not assume that this is the case and instead open up for the possibility that in the infinitely small there may be other length functions, there may be other inner products on the tangent space! A Riemannian manifold is a smooth manifold equipped with inner product, which may or may not be the Euclidean inner product, on each tangent space. 1. Riemannian metric 2.1. Definition. A Riemannian metric on a smooth manifold M is a symmetric, positive 2 definite -tensor g ∈ T 2(M). 0 0 In a coordinate frame we may write i j g = gijdx ⊗ dx , gij = g(∂i, ∂j) i j i j This means that g(U ∂i,V ∂j) = gijU V and in particular that (2.1) h∂i, ∂ii = gii, h∂i, ∂ji = gij 1 Note that there are only 2 n(n + 1) different functions here as gij = gji by symmetry. 2.2. Remark. Since the metric tensor is symmetric, it is traditional to write it in a basis of symmetric tensors. The symmetrization of ω ⊗ η is the tensor 1 ωη = (ω ⊗ η + η ⊗ ω) 2 Note that ωη = ηω and that ω2 = ωω = ω ⊗ ω. Observe that n i j X i 2 X i j g = gijdx dx = 2 gii(dx ) + 2 gijdx dx i=1 1≤i<j≤n 2.3. Lemma. Let F : M → N be an immersion and g a Riemannian metric on N. (1) F ∗g is a Riemannian metric on M. i j (2) If g = gijdy dy in a coordinate frame on N, then ∗ −1 i j F (g)|F (U) = gijdy F dy F Proof. It is a general fact that F ∗(g) is a smooth 2-form on M (1.9). F ∗(g) is symmetric because g is symmetric and it is positive definite because g is positive definite and F∗ is injective ∗ i j (1.9) ∗ i ∗ j (1.4) i j on each fibre. F (gijdy dy ) = gijF dy F dy = gijdy F dy F . For instance if F : U → M is a parameterization (an inverse chart) of an open subset of M ⊂ Rm, then the pull-back of the induced metric on M is m ∗ ∗ i j i j X i 2 (2.4) F (g) = F (δijdx dx ) = δijdF dF = (dF ) i=1 These expressions are tensor fields living in the tensor algebra T ∗(M) of M. 7 8 2. RIEMANNIAN MANIFOLDS 2.5. Example. (Graphs) Let M ⊂ Rn × R be the graph of the smooth function f : M → R. Then s(x) = (x, f(x)) is a diffeomorphism so that the Riemannian manifold (M, ι∗gn+1) is isometric to (Rn, s∗gn+1) where the metric s∗gn+1 is n+1 n n X X ∂f 2 X ∂f ∂f s∗( (dxi)2) = (dxi)2 + dxi = (dxi)2 + dxidxj ∂xi ∂xi ∂xj i=1 i=1 i=1 n ∂f ∂f X ∂f X ∂f ∂f = δ + dxidxj = 1 + ( )2(dxi)2 + 2 dxidxj ij ∂xi ∂xj ∂xi ∂xi ∂xj i=1 1≤i<j≤n 2 2 3 2.6. Example. let S+ be the upper hemisphere on S ⊂ R considered as the graph of the p 2 2 2 2 2 ∗ 3 function f(x, y) = 1 − x − y defined on the unit ball B ⊂ R . Then (S+, ι g ) is isometric to (B2, s∗g3) where !2 −x −y s∗g3 = (dx)2 + (dy)2 + dx + dy p1 − x2 − y2 p1 − x2 − y2 1 − y2 1 − x2 2xy = (dx)2 + (dy)2 + dxdy 1 − x2 − y2 1 − x2 − y2 1 − x2 − y2 This means (2.1) that 1 − y2 1 − x2 xy h∂ , ∂ i = , h∂ , ∂ i = , h∂ , ∂ i = x x 1 − x2 − y2 y y 1 − x2 − y2 x y 1 − x2 − y2 2 at the point (x, y) ∈ B .
Load more

Recommended publications
  • Examples of Manifolds
    Examples of Manifolds Example 1 (Open Subset of IRn) Any open subset, O, of IRn is a manifold of dimension n. One possible atlas is A = (O, ϕid) , where ϕid is the identity map. That is, ϕid(x) = x. n Of course one possible choice of O is IR itself. Example 2 (The Circle) The circle S1 = (x,y) ∈ IR2 x2 + y2 = 1 is a manifold of dimension one. One possible atlas is A = {(U , ϕ ), (U , ϕ )} where 1 1 1 2 1 y U1 = S \{(−1, 0)} ϕ1(x,y) = arctan x with − π < ϕ1(x,y) <π ϕ1 1 y U2 = S \{(1, 0)} ϕ2(x,y) = arctan x with 0 < ϕ2(x,y) < 2π U1 n n n+1 2 2 Example 3 (S ) The n–sphere S = x =(x1, ··· ,xn+1) ∈ IR x1 +···+xn+1 =1 n A U , ϕ , V ,ψ i n is a manifold of dimension . One possible atlas is 1 = ( i i) ( i i) 1 ≤ ≤ +1 where, for each 1 ≤ i ≤ n + 1, n Ui = (x1, ··· ,xn+1) ∈ S xi > 0 ϕi(x1, ··· ,xn+1)=(x1, ··· ,xi−1,xi+1, ··· ,xn+1) n Vi = (x1, ··· ,xn+1) ∈ S xi < 0 ψi(x1, ··· ,xn+1)=(x1, ··· ,xi−1,xi+1, ··· ,xn+1) n So both ϕi and ψi project onto IR , viewed as the hyperplane xi = 0. Another possible atlas is n n A2 = S \{(0, ··· , 0, 1)}, ϕ , S \{(0, ··· , 0, −1)},ψ where 2x1 2xn ϕ(x , ··· ,xn ) = , ··· , 1 +1 1−xn+1 1−xn+1 2x1 2xn ψ(x , ··· ,xn ) = , ··· , 1 +1 1+xn+1 1+xn+1 are the stereographic projections from the north and south poles, respectively.
    [Show full text]
  • An Introduction to Topology the Classification Theorem for Surfaces by E
    An Introduction to Topology An Introduction to Topology The Classification theorem for Surfaces By E. C. Zeeman Introduction. The classification theorem is a beautiful example of geometric topology. Although it was discovered in the last century*, yet it manages to convey the spirit of present day research. The proof that we give here is elementary, and its is hoped more intuitive than that found in most textbooks, but in none the less rigorous. It is designed for readers who have never done any topology before. It is the sort of mathematics that could be taught in schools both to foster geometric intuition, and to counteract the present day alarming tendency to drop geometry. It is profound, and yet preserves a sense of fun. In Appendix 1 we explain how a deeper result can be proved if one has available the more sophisticated tools of analytic topology and algebraic topology. Examples. Before starting the theorem let us look at a few examples of surfaces. In any branch of mathematics it is always a good thing to start with examples, because they are the source of our intuition. All the following pictures are of surfaces in 3-dimensions. In example 1 by the word “sphere” we mean just the surface of the sphere, and not the inside. In fact in all the examples we mean just the surface and not the solid inside. 1. Sphere. 2. Torus (or inner tube). 3. Knotted torus. 4. Sphere with knotted torus bored through it. * Zeeman wrote this article in the mid-twentieth century. 1 An Introduction to Topology 5.
    [Show full text]
  • The Sphere Project
    ;OL :WOLYL 7YVQLJ[ +XPDQLWDULDQ&KDUWHUDQG0LQLPXP 6WDQGDUGVLQ+XPDQLWDULDQ5HVSRQVH ;OL:WOLYL7YVQLJ[ 7KHULJKWWROLIHZLWKGLJQLW\ ;OL:WOLYL7YVQLJ[PZHUPUP[PH[P]L[VKL[LYTPULHUK WYVTV[LZ[HUKHYKZI`^OPJO[OLNSVIHSJVTT\UP[` /\THUP[HYPHU*OHY[LY YLZWVUKZ[V[OLWSPNO[VMWLVWSLHMMLJ[LKI`KPZHZ[LYZ /\THUP[HYPHU >P[O[OPZ/HUKIVVR:WOLYLPZ^VYRPUNMVYH^VYSKPU^OPJO [OLYPNO[VMHSSWLVWSLHMMLJ[LKI`KPZHZ[LYZ[VYLLZ[HISPZO[OLPY *OHY[LYHUK SP]LZHUKSP]LSPOVVKZPZYLJVNUPZLKHUKHJ[LK\WVUPU^H`Z[OH[ YLZWLJ[[OLPY]VPJLHUKWYVTV[L[OLPYKPNUP[`HUKZLJ\YP[` 4PUPT\T:[HUKHYKZ This Handbook contains: PU/\THUP[HYPHU (/\THUP[HYPHU*OHY[LY!SLNHSHUKTVYHSWYPUJPWSLZ^OPJO HUK YLÅLJ[[OLYPNO[ZVMKPZHZ[LYHMMLJ[LKWVW\SH[PVUZ 4PUPT\T:[HUKHYKZPU/\THUP[HYPHU9LZWVUZL 9LZWVUZL 7YV[LJ[PVU7YPUJPWSLZ *VYL:[HUKHYKZHUKTPUPT\TZ[HUKHYKZPUMV\YRL`SPMLZH]PUN O\THUP[HYPHUZLJ[VYZ!>H[LYZ\WWS`ZHUP[H[PVUHUKO`NPLUL WYVTV[PVU"-VVKZLJ\YP[`HUKU\[YP[PVU":OLS[LYZL[[SLTLU[HUK UVUMVVKP[LTZ"/LHS[OHJ[PVU;OL`KLZJYPILwhat needs to be achieved in a humanitarian response in order for disaster- affected populations to survive and recover in stable conditions and with dignity. ;OL:WOLYL/HUKIVVRLUQV`ZIYVHKV^ULYZOPWI`HNLUJPLZHUK PUKP]PK\HSZVMMLYPUN[OLO\THUP[HYPHUZLJ[VYH common language for working together towards quality and accountability in disaster and conflict situations ;OL:WOLYL/HUKIVVROHZHU\TILYVMºJVTWHUPVU Z[HUKHYKZ»L_[LUKPUNP[ZZJVWLPUYLZWVUZL[VULLKZ[OH[ OH]LLTLYNLK^P[OPU[OLO\THUP[HYPHUZLJ[VY ;OL:WOLYL7YVQLJ[^HZPUP[PH[LKPU I`HU\TILY VMO\THUP[HYPHU5.6ZHUK[OL9LK*YVZZHUK 9LK*YLZJLU[4V]LTLU[ ,+0;065 7KHB6SKHUHB3URMHFWBFRYHUBHQBLQGG The Sphere Project Humanitarian Charter and Minimum Standards in Humanitarian Response Published by: The Sphere Project Copyright@The Sphere Project 2011 Email: [email protected] Website : www.sphereproject.org The Sphere Project was initiated in 1997 by a group of NGOs and the Red Cross and Red Crescent Movement to develop a set of universal minimum standards in core areas of humanitarian response: the Sphere Handbook.
    [Show full text]
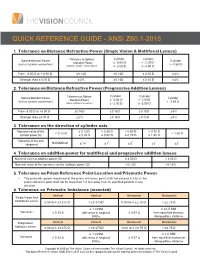
  • Quick Reference Guide - Ansi Z80.1-2015
    QUICK REFERENCE GUIDE - ANSI Z80.1-2015 1. Tolerance on Distance Refractive Power (Single Vision & Multifocal Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -4.50 D (minus cylinder convention) ≤ -2.00 D ≤ -4.50 D From - 6.50 D to + 6.50 D ± 0.13 D ± 0.13 D ± 0.15 D ± 4% Stronger than ± 6.50 D ± 2% ± 0.13 D ± 0.15 D ± 4% 2. Tolerance on Distance Refractive Power (Progressive Addition Lenses) Cylinder Cylinder Sphere Meridian Power Tolerance on Sphere Cylinder Meridian Power ≥ 0.00 D > - 2.00 D (minus cylinder convention) > -3.50 D (minus cylinder convention) ≤ -2.00 D ≤ -3.50 D From -8.00 D to +8.00 D ± 0.16 D ± 0.16 D ± 0.18 D ± 5% Stronger than ±8.00 D ± 2% ± 0.16 D ± 0.18 D ± 5% 3. Tolerance on the direction of cylinder axis Nominal value of the ≥ 0.12 D > 0.25 D > 0.50 D > 0.75 D < 0.12 D > 1.50 D cylinder power (D) ≤ 0.25 D ≤ 0.50 D ≤ 0.75 D ≤ 1.50 D Tolerance of the axis Not Defined ° ° ° ° ° (degrees) ± 14 ± 7 ± 5 ± 3 ± 2 4. Tolerance on addition power for multifocal and progressive addition lenses Nominal value of addition power (D) ≤ 4.00 D > 4.00 D Nominal value of the tolerance on the addition power (D) ± 0.12 D ± 0.18 D 5. Tolerance on Prism Reference Point Location and Prismatic Power • The prismatic power measured at the prism reference point shall not exceed 0.33Δ or the prism reference point shall not be more than 1.0 mm away from its specified position in any direction.
    [Show full text]
  • Riemannian Geometry and the General Theory of Relativity
    University of Montana ScholarWorks at University of Montana Graduate Student Theses, Dissertations, & Professional Papers Graduate School 1967 Riemannian geometry and the general theory of relativity Marie McBride Vanisko The University of Montana Follow this and additional works at: https://scholarworks.umt.edu/etd Let us know how access to this document benefits ou.y Recommended Citation Vanisko, Marie McBride, "Riemannian geometry and the general theory of relativity" (1967). Graduate Student Theses, Dissertations, & Professional Papers. 8075. https://scholarworks.umt.edu/etd/8075 This Thesis is brought to you for free and open access by the Graduate School at ScholarWorks at University of Montana. It has been accepted for inclusion in Graduate Student Theses, Dissertations, & Professional Papers by an authorized administrator of ScholarWorks at University of Montana. For more information, please contact [email protected]. p m TH3 OmERAl THEORY OF RELATIVITY By Marie McBride Vanisko B.A., Carroll College, 1965 Presented in partial fulfillment of the requirements for the degree of Master of Arts UNIVERSITY OF MOKT/JTA 1967 Approved by: Chairman, Board of Examiners D e a ^ Graduante school V AUG 8 1967, Reproduced with permission of the copyright owner. Further reproduction prohibited without permission. V W Number: EP38876 All rights reserved INFORMATION TO ALL USERS The quality of this reproduotion is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a complete manuscript and there are missir^ pages, these will be noted. Also, if matedal had to be removed, a note will indicate the deletion. UMT Oi*MMtion neiitNna UMi EP38876 Published ProQuest LLQ (2013).
    [Show full text]
  • Riemannian Geometry Learning for Disease Progression Modelling Maxime Louis, Raphäel Couronné, Igor Koval, Benjamin Charlier, Stanley Durrleman
    Riemannian geometry learning for disease progression modelling Maxime Louis, Raphäel Couronné, Igor Koval, Benjamin Charlier, Stanley Durrleman To cite this version: Maxime Louis, Raphäel Couronné, Igor Koval, Benjamin Charlier, Stanley Durrleman. Riemannian geometry learning for disease progression modelling. 2019. hal-02079820v2 HAL Id: hal-02079820 https://hal.archives-ouvertes.fr/hal-02079820v2 Preprint submitted on 17 Apr 2019 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Riemannian geometry learning for disease progression modelling Maxime Louis1;2, Rapha¨elCouronn´e1;2, Igor Koval1;2, Benjamin Charlier1;3, and Stanley Durrleman1;2 1 Sorbonne Universit´es,UPMC Univ Paris 06, Inserm, CNRS, Institut du cerveau et de la moelle (ICM) 2 Inria Paris, Aramis project-team, 75013, Paris, France 3 Institut Montpelli`erainAlexander Grothendieck, CNRS, Univ. Montpellier Abstract. The analysis of longitudinal trajectories is a longstanding problem in medical imaging which is often tackled in the context of Riemannian geometry: the set of observations is assumed to lie on an a priori known Riemannian manifold. When dealing with high-dimensional or complex data, it is in general not possible to design a Riemannian geometry of relevance. In this paper, we perform Riemannian manifold learning in association with the statistical task of longitudinal trajectory analysis.
    [Show full text]
  • On Jacobi Field Splitting Theorems 3
    ON JACOBI FIELD SPLITTING THEOREMS DENNIS GUMAER AND FREDERICK WILHELM Abstract. We formulate extensions of Wilking’s Jacobi field splitting theorem to uniformly positive sectional curvature and also to positive and nonnegative intermediate Ricci curva- tures. In [Wilk1], Wilking established the following remarkable Jacobi field splitting theorem. Theorem A. (Wilking) Let γ be a unit speed geodesic in a complete Riemannian n–manifold M with nonnegative curvature. Let Λ be an (n−1)-dimensional space of Jacobi fields orthogonal to γ on which the Riccati operator S is self-adjoint. Then Λ splits orthogonally into Λ = span{J ∈ Λ | J(t)=0 for some t}⊕{J ∈ Λ | J is parallel}. This result has several impressive applications, so it is natural to ask about analogs for other curvature conditions. We provide these analogs for positive sectional curvature and also for nonnegative and positive intermediate Ricci curvatures. For positive curvature our result is the following. Theorem B. Let M be a complete n-dimensional Riemannian manifold with sec ≥ 1. For α ∈ [0, π), let γ :[α, π] −→ M be a unit speed geodesic, and let Λ be an (n − 1)-dimensional family of Jacobi fields orthogonal to γ on which the Riccati operator S is self-adjoint. If max{eigenvalue S(α)} ≤ cot α, then Λ splits orthogonally into (1) span{J ∈ Λ | J (t)=0 for some t ∈ (α, π)}⊕{J ∈ Λ |J = sin(t)E(t) with E parallel}. Notice that for α = 0, the boundary inequality, max{eigenvalue S(α)} ≤ cot α = ∞, is arXiv:1405.1110v2 [math.DG] 5 Oct 2014 always satisfied.
    [Show full text]
  • An Introduction to Riemannian Geometry with Applications to Mechanics and Relativity
    An Introduction to Riemannian Geometry with Applications to Mechanics and Relativity Leonor Godinho and Jos´eNat´ario Lisbon, 2004 Contents Chapter 1. Differentiable Manifolds 3 1. Topological Manifolds 3 2. Differentiable Manifolds 9 3. Differentiable Maps 13 4. Tangent Space 15 5. Immersions and Embeddings 22 6. Vector Fields 26 7. Lie Groups 33 8. Orientability 45 9. Manifolds with Boundary 48 10. Notes on Chapter 1 51 Chapter 2. Differential Forms 57 1. Tensors 57 2. Tensor Fields 64 3. Differential Forms 66 4. Integration on Manifolds 72 5. Stokes Theorem 75 6. Orientation and Volume Forms 78 7. Notes on Chapter 2 80 Chapter 3. Riemannian Manifolds 87 1. Riemannian Manifolds 87 2. Affine Connections 94 3. Levi-Civita Connection 98 4. Minimizing Properties of Geodesics 104 5. Hopf-Rinow Theorem 111 6. Notes on Chapter 3 114 Chapter 4. Curvature 115 1. Curvature 115 2. Cartan’s Structure Equations 122 3. Gauss-Bonnet Theorem 131 4. Manifolds of Constant Curvature 137 5. Isometric Immersions 144 6. Notes on Chapter 4 150 1 2 CONTENTS Chapter 5. Geometric Mechanics 151 1. Mechanical Systems 151 2. Holonomic Constraints 160 3. Rigid Body 164 4. Non-Holonomic Constraints 177 5. Lagrangian Mechanics 186 6. Hamiltonian Mechanics 194 7. Completely Integrable Systems 203 8. Notes on Chapter 5 209 Chapter 6. Relativity 211 1. Galileo Spacetime 211 2. Special Relativity 213 3. The Cartan Connection 223 4. General Relativity 224 5. The Schwarzschild Solution 229 6. Cosmology 240 7. Causality 245 8. Singularity Theorem 253 9. Notes on Chapter 6 263 Bibliography 265 Index 267 CHAPTER 1 Differentiable Manifolds This chapter introduces the basic notions of differential geometry.
    [Show full text]
  • Riemannian Geometry and Multilinear Tensors with Vector Fields on Manifolds Md
    International Journal of Scientific & Engineering Research, Volume 5, Issue 9, September-2014 157 ISSN 2229-5518 Riemannian Geometry and Multilinear Tensors with Vector Fields on Manifolds Md. Abdul Halim Sajal Saha Md Shafiqul Islam Abstract-In the paper some aspects of Riemannian manifolds, pseudo-Riemannian manifolds, Lorentz manifolds, Riemannian metrics, affine connections, parallel transport, curvature tensors, torsion tensors, killing vector fields, conformal killing vector fields are focused. The purpose of this paper is to develop the theory of manifolds equipped with Riemannian metric. I have developed some theorems on torsion and Riemannian curvature tensors using affine connection. A Theorem 1.20 named “Fundamental Theorem of Pseudo-Riemannian Geometry” has been established on Riemannian geometry using tensors with metric. The main tools used in the theorem of pseudo Riemannian are tensors fields defined on a Riemannian manifold. Keywords: Riemannian manifolds, pseudo-Riemannian manifolds, Lorentz manifolds, Riemannian metrics, affine connections, parallel transport, curvature tensors, torsion tensors, killing vector fields, conformal killing vector fields. —————————— —————————— I. Introduction (c) { } is a family of open sets which covers , that is, 푖 = . Riemannian manifold is a pair ( , g) consisting of smooth 푈 푀 manifold and Riemannian metric g. A manifold may carry a (d) ⋃ is푈 푖푖 a homeomorphism푀 from onto an open subset of 푀 ′ further structure if it is endowed with a metric tensor, which is a 푖 . 푖 푖 휑 푈 푈 natural generation푀 of the inner product between two vectors in 푛 ℝ to an arbitrary manifold. Riemannian metrics, affine (e) Given and such that , the map = connections,푛 parallel transport, curvature tensors, torsion tensors, ( ( ) killingℝ vector fields and conformal killing vector fields play from푖 푗 ) to 푖 푗 is infinitely푖푗 −1 푈 푈 푈 ∩ 푈 ≠ ∅ 휓 important role to develop the theorem of Riemannian manifolds.
    [Show full text]
  • Hadamaard's Theorem and Jacobi Fields
    Lecture 35: Hadamaard’s Theorem and Jacobi Fields Last time I stated: Theorem 35.1. Let (M,g) be a complete Riemannian manifold. Assume that for every p M and for every x, y T M, we have ∈ ∈ p K(x, y) 0. ≤ Then for any p M,theexponentialmap ∈ exp : T M M p p → is a covering map. 1. Jacobi fields—surfaces from families of tangent vectors Last time I also asked you to consider the following set-up: Let w : ( ,) TpM be a family of tangent vectors. Then for every tangent vector w−(s), we→ can consider the geodesic at p with tangent vector w(s). This defines amap f :( ,) (a, b) M, (s, t) γ (t)=exp(tw(s)). − × → → w(s) p Fixing s =0,notethatf(0,t)=γ(t)isageodesic,andthereisavectorfield ∂ f ∂s (0,t) which is a section of γ TM—e.g., a smooth map ∗ J :(a, b) γ∗TM. → Proposition 35.2. Let ∂ J(t)= f. ∂s (0,t) Then J satisfies the differential equation J =Ω(˙γ(t),J(t))γ ˙ (t). ∇∂t ∇∂t 117 Chit-chat 35.3. As a consequence, the acceleration of J is determined com- pletely by the curvature’s affect on the velocity of the geodesic and the value of J. Definition 35.4 (Jacobi fields). Let γ be a geodesic. Then any vector field along γ satisfying the above differential equation is called a Jacobi field. Remark 35.5. When confronted with an expression like Y or ∇X ∇X ∇Y there are only two ways to swap the order of the differentiation: Using the fact that one has a torsion-free connection, so Y = X +[X, Y ] ∇X ∇Y or by using the definition of the curvature tensor: = + +Ω(X, Y ).
    [Show full text]
  • Riemann's Contribution to Differential Geometry
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Historia Mathematics 9 (1982) l-18 RIEMANN'S CONTRIBUTION TO DIFFERENTIAL GEOMETRY BY ESTHER PORTNOY UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN, URBANA, IL 61801 SUMMARIES In order to make a reasonable assessment of the significance of Riemann's role in the history of dif- ferential geometry, not unduly influenced by his rep- utation as a great mathematician, we must examine the contents of his geometric writings and consider the response of other mathematicians in the years immedi- ately following their publication. Pour juger adkquatement le role de Riemann dans le developpement de la geometric differentielle sans etre influence outre mesure par sa reputation de trks grand mathematicien, nous devons &udier le contenu de ses travaux en geometric et prendre en consideration les reactions des autres mathematiciens au tours de trois an&es qui suivirent leur publication. Urn Riemann's Einfluss auf die Entwicklung der Differentialgeometrie richtig einzuschZtzen, ohne sich von seinem Ruf als bedeutender Mathematiker iiberm;issig beeindrucken zu lassen, ist es notwendig den Inhalt seiner geometrischen Schriften und die Haltung zeitgen&sischer Mathematiker unmittelbar nach ihrer Verijffentlichung zu untersuchen. On June 10, 1854, Georg Friedrich Bernhard Riemann read his probationary lecture, "iber die Hypothesen welche der Geometrie zu Grunde liegen," before the Philosophical Faculty at Gdttingen ill. His biographer, Dedekind [1892, 5491, reported that Riemann had worked hard to make the lecture understandable to nonmathematicians in the audience, and that the result was a masterpiece of presentation, in which the ideas were set forth clearly without the aid of analytic techniques.
    [Show full text]
  • Chapter 13 Curvature in Riemannian Manifolds
    Chapter 13 Curvature in Riemannian Manifolds 13.1 The Curvature Tensor If (M, , )isaRiemannianmanifoldand is a connection on M (that is, a connection on TM−), we− saw in Section 11.2 (Proposition 11.8)∇ that the curvature induced by is given by ∇ R(X, Y )= , ∇X ◦∇Y −∇Y ◦∇X −∇[X,Y ] for all X, Y X(M), with R(X, Y ) Γ( om(TM,TM)) = Hom (Γ(TM), Γ(TM)). ∈ ∈ H ∼ C∞(M) Since sections of the tangent bundle are vector fields (Γ(TM)=X(M)), R defines a map R: X(M) X(M) X(M) X(M), × × −→ and, as we observed just after stating Proposition 11.8, R(X, Y )Z is C∞(M)-linear in X, Y, Z and skew-symmetric in X and Y .ItfollowsthatR defines a (1, 3)-tensor, also denoted R, with R : T M T M T M T M. p p × p × p −→ p Experience shows that it is useful to consider the (0, 4)-tensor, also denoted R,givenby R (x, y, z, w)= R (x, y)z,w p p p as well as the expression R(x, y, y, x), which, for an orthonormal pair, of vectors (x, y), is known as the sectional curvature, K(x, y). This last expression brings up a dilemma regarding the choice for the sign of R. With our present choice, the sectional curvature, K(x, y), is given by K(x, y)=R(x, y, y, x)but many authors define K as K(x, y)=R(x, y, x, y). Since R(x, y)isskew-symmetricinx, y, the latter choice corresponds to using R(x, y)insteadofR(x, y), that is, to define R(X, Y ) by − R(X, Y )= + .
    [Show full text]