Biased Estimators of Quantitative Trait Locus Heritability and Location in Interval Mapping
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Lineage-Specific Mapping of Quantitative Trait Loci
Heredity (2013) 111, 106–113 & 2013 Macmillan Publishers Limited All rights reserved 0018-067X/13 www.nature.com/hdy ORIGINAL ARTICLE Lineage-specific mapping of quantitative trait loci C Chen1 and K Ritland We present an approach for quantitative trait locus (QTL) mapping, termed as ‘lineage-specific QTL mapping’, for inferring allelic changes of QTL evolution along with branches in a phylogeny. We describe and analyze the simplest case: by adding a third taxon into the normal procedure of QTL mapping between pairs of taxa, such inferences can be made along lineages to a presumed common ancestor. Although comparisons of QTL maps among species can identify homology of QTLs by apparent co- location, lineage-specific mapping of QTL can classify homology into (1) orthology (shared origin of QTL) versus (2) paralogy (independent origin of QTL within resolution of map distance). In this light, we present a graphical method that identifies six modes of QTL evolution in a three taxon comparison. We then apply our model to map lineage-specific QTLs for inbreeding among three taxa of yellow monkey-flower: Mimulus guttatus and two inbreeders M. platycalyx and M. micranthus, but critically assuming outcrossing was the ancestral state. The two most common modes of homology across traits were orthologous (shared ancestry of mutation for QTL alleles). The outbreeder M. guttatus had the fewest lineage-specific QTL, in accordance with the presumed ancestry of outbreeding. Extensions of lineage-specific QTL mapping to other types of data and crosses, and to inference of ancestral QTL state, are discussed. Heredity (2013) 111, 106–113; doi:10.1038/hdy.2013.24; published online 24 April 2013 Keywords: Quantitative trait locus mapping; evolution of mating systems; Mimulus INTRODUCTION common ancestor of these two taxa, back to the common ancestor of Knowledge of the genetic architecture of complex traits can offer all three taxa and forwards again to the third taxon. -
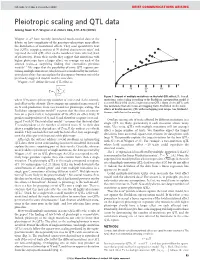
Pleiotropic Scaling and QTL Data Arising From: G
NATURE | Vol 456 | 4 December 2008 BRIEF COMMUNICATIONS ARISING Pleiotropic scaling and QTL data Arising from: G. P. Wagner et al. Nature 452, 470–473 (2008) Wagner et al.1 have recently introduced much-needed data to the debate on how complexity of the genotype–phenotype map affects the distribution of mutational effects. They used quantitative trait loci (QTLs) mapping analysis of 70 skeletal characters in mice2 and regressed the total QTL effect on the number of traits affected (level of pleiotropy). From their results they suggest that mutations with higher pleiotropy have a larger effect, on average, on each of the T affected traits—a surprising finding that contradicts previous models3–7. We argue that the possibility of some QTL regions con- taining multiple mutations, which was not considered by the authors, introduces a bias that can explain the discrepancy between one of the previously suggested models and the new data. Wagner et al.1 define the total QTL effect as vffiffiffiffiffiffiffiffiffiffiffiffiffi u uXN 10 20 30 ~t 2 T Ai N i~1 Figure 1 | Impact of multiple mutations on the total QTL effect, T. For all where N measures pleiotropy (number of traits) and Ai the normal- mutations, strict scaling according to the Euclidean superposition model is ized effect on the ith trait. They compare an empirical regression of T assumed. Black filled circles, single-mutation QTLs. Open circles, QTLs with on N with predictions from two models for pleiotropic scaling. The two mutations that affect non-overlapping traits. Red filled circles, total Euclidean superposition model3,4 assumes that the effect of a muta- effects of double-mutant QTL with overlapping trait ranges (see Methods). -

1 ROBERT PLOMIN on Behavioral Genetics Genetic Links Common
Genetic links • Background – Why has educational psychology ben so slow ROBERT PLOMIN to accept genetics? on Behavioral Genetics • Beyond nature vs. nurture – 3 findings from genetic research with far- reaching implications for education: October, 2004 The nature of nurture The abnormal is normal Generalist genes • Molecular Genetics Quantitative genetics: twin and adoption studies Common medical disorders Identical twins Fraternal twins (monozygotic, MZ) (dizygotic, DZ) 1 Twin concordances in TEDS at 7 years Twins Early Development Study (TEDS) for low reading and maths Perceptions of nature/nurture: % parents (N=1340) and teachers Beyond nature vs. nurture: (N=667) indicating that genes are at least as important as environment (Walker & Plomin, Ed. Psych., in press) The nature of nurture • Genetic influence on experience • Genotype-environment correlation – Children’s genetic propensities are correlated with their experiences passive evocative active 2 Beyond nature vs. nurture: Genotype-environment correlation The nature of nurture • Passive • Genotype-environment correlation – e.g., family background (SES) and school – Children’s genetic propensities are correlated with achievement their experiences passive • Evocative evocative – Children evoke experiences for genetic reasons Active • Active • Molecular genetics – Children actively create environments that foster – Find genes associated with learning experiences their genetic propensities Beyond nature vs. nurture: The one-gene one-disability (OGOD) model The abnormal is normal • Common learning disabilities are the quantitative extreme of the same genetic and environmental factors responsible for normal variation in learning abilities. • There are no common learning disabilities, just the extremes of normal variation. 3 OGOD (rare) and QTL (common) disorders The quantitative trait locus (QTL) model Beyond nature vs. -

Epigenome-Wide Study Identified Methylation Sites Associated With
nutrients Article Epigenome-Wide Study Identified Methylation Sites Associated with the Risk of Obesity Majid Nikpay 1,*, Sepehr Ravati 2, Robert Dent 3 and Ruth McPherson 1,4,* 1 Ruddy Canadian Cardiovascular Genetics Centre, University of Ottawa Heart Institute, 40 Ruskin St–H4208, Ottawa, ON K1Y 4W7, Canada 2 Plastenor Technologies Company, Montreal, QC H2P 2G4, Canada; [email protected] 3 Department of Medicine, Division of Endocrinology, University of Ottawa, the Ottawa Hospital, Ottawa, ON K1Y 4E9, Canada; [email protected] 4 Atherogenomics Laboratory, University of Ottawa Heart Institute, Ottawa, ON K1Y 4W7, Canada * Correspondence: [email protected] (M.N.); [email protected] (R.M.) Abstract: Here, we performed a genome-wide search for methylation sites that contribute to the risk of obesity. We integrated methylation quantitative trait locus (mQTL) data with BMI GWAS information through a SNP-based multiomics approach to identify genomic regions where mQTLs for a methylation site co-localize with obesity risk SNPs. We then tested whether the identified site contributed to BMI through Mendelian randomization. We identified multiple methylation sites causally contributing to the risk of obesity. We validated these findings through a replication stage. By integrating expression quantitative trait locus (eQTL) data, we noted that lower methylation at cg21178254 site upstream of CCNL1 contributes to obesity by increasing the expression of this gene. Higher methylation at cg02814054 increases the risk of obesity by lowering the expression of MAST3, whereas lower methylation at cg06028605 contributes to obesity by decreasing the expression of SLC5A11. Finally, we noted that rare variants within 2p23.3 impact obesity by making the cg01884057 Citation: Nikpay, M.; Ravati, S.; Dent, R.; McPherson, R. -

QUANTITATIVE TRAIT LOCUS ANALYSIS: in Several Variants (I.E., Alleles)
TECHNOLOGIES FROM THE FIELD QUANTITATIVE TRAIT LOCUS ANALYSIS: in several variants (i.e., alleles). QTL analysis allows one MULTIPLE CROSS AND HETEROGENEOUS to map, with some precision, the genomic position of STOCK MAPPING these alleles. For many researchers in the alcohol field, the break Robert Hitzemann, Ph.D.; John K. Belknap, Ph.D.; through with respect to the genetic determination of alcohol- and Shannon K. McWeeney, Ph.D. related behaviors occurred when Plomin and colleagues (1991) made the seminal observation that a specific panel of RI mice (i.e., the BXD panel) could be used to identify KEY WORDS: Genetic theory of alcohol and other drug use; genetic the physical location of (i.e., to map) QTLs for behavioral factors; environmental factors; behavioral phenotype; behavioral phenotypes. Because the phenotypes of the different strains trait; quantitative trait gene (QTG); inbred animal strains; in this panel had been determined for many alcohol- recombinant inbred (RI) mouse strains; quantitative traits; related traits, researchers could readily apply the strategy quantitative trait locus (QTL) mapping; multiple cross mapping of RI–QTL mapping (Gora-Maslak et al. 1991). Although (MCM); heterogeneous stock (HS) mapping; microsatellite investigators recognized early on that this panel was not mapping; animal models extensive enough to answer all questions, the emerging data illustrated the rich genetic complexity of alcohol- related phenotypes (Belknap 1992; Plomin and McClearn ntil well into the 1990s, both preclinical and clinical 1993). research focused on finding “the” gene for human The next advance came with the development of diseases, including alcoholism. This focus was rein U microsatellite maps (Dietrich et al. -

Article the Power to Detect Quantitative Trait Loci Using
The Power to Detect Quantitative Trait Loci Using Resequenced, Experimentally Evolved Populations of Diploid, Sexual Organisms James G. Baldwin-Brown,*,1 Anthony D. Long,1 and Kevin R. Thornton1 1Department of Ecology and Evolutionary Biology, University of California, Irvine *Corresponding author: E-mail: [email protected]. Associate editor: John Parsch Abstract A novel approach for dissecting complex traits is to experimentally evolve laboratory populations under a controlled environment shift, resequence the resulting populations, and identify single nucleotide polymorphisms (SNPs) and/or genomic regions highly diverged in allele frequency. To better understand the power and localization ability of such an evolve and resequence (E&R) approach, we carried out forward-in-time population genetics simulations of 1 Mb genomic regions under a large combination of experimental conditions, then attempted to detect significantly diverged SNPs. Our analysis indicates that the ability to detect differentiation between populations is primarily affected by selection coef- ficient, population size, number of replicate populations, and number of founding haplotypes. We estimate that E&R studies can detect and localize causative sites with 80% success or greater when the number of founder haplotypes is over 500, experimental populations are replicated at least 25-fold, population size is at least 1,000 diploid individuals, and the selection coefficient on the locus of interest is at least 0.1. More achievable experimental designs (less replicated, fewer founder haplotypes, smaller effective population size, and smaller selection coefficients) can have power of greater than 50% to identify a handful of SNPs of which one is likely causative. Similarly, in cases where s 0.2, less demanding experimental designs can yield high power. -

Glossary/Index
Glossary 03/08/2004 9:58 AM Page 119 GLOSSARY/INDEX The numbers after each term represent the chapter in which it first appears. additive 2 allele 2 When an allele’s contribution to the variation in a One of two or more alternative forms of a gene; a single phenotype is separately measurable; the independent allele for each gene is inherited separately from each effects of alleles “add up.” Antonym of nonadditive. parent. ADHD/ADD 6 Alzheimer’s disease 5 Attention Deficit Hyperactivity Disorder/Attention A medical disorder causing the loss of memory, rea- Deficit Disorder. Neurobehavioral disorders character- soning, and language abilities. Protein residues called ized by an attention span or ability to concentrate that is plaques and tangles build up and interfere with brain less than expected for a person's age. With ADHD, there function. This disorder usually first appears in persons also is age-inappropriate hyperactivity, impulsive over age sixty-five. Compare to early-onset Alzheimer’s. behavior or lack of inhibition. There are several types of ADHD: a predominantly inattentive subtype, a predomi- amino acids 2 nantly hyperactive-impulsive subtype, and a combined Molecules that are combined to form proteins. subtype. The condition can be cognitive alone or both The sequence of amino acids in a protein, and hence pro- cognitive and behavioral. tein function, is determined by the genetic code. adoption study 4 amnesia 5 A type of research focused on families that include one Loss of memory, temporary or permanent, that can result or more children raised by persons other than their from brain injury, illness, or trauma. -

Mapping Quantitative Trait Loci in Selected Breeding Populations: a Segregation Distortion Approach
Heredity (2015) 115, 538–546 & 2015 Macmillan Publishers Limited All rights reserved 0018-067X/15 www.nature.com/hdy ORIGINAL ARTICLE Mapping quantitative trait loci in selected breeding populations: A segregation distortion approach Y Cui1,2, F Zhang1,JXu1,3,ZLi1 and S Xu2 Quantitative trait locus (QTL) mapping is often conducted in line-crossing experiments where a sample of individuals is randomly selected from a pool of all potential progeny. QTLs detected from such an experiment are important for us to understand the genetic mechanisms governing a complex trait, but may not be directly relevant to plant breeding if they are not detected from the breeding population where selection is targeting for. QTLs segregating in one population may not necessarily segregate in another population. To facilitate marker-assisted selection, QTLs must be detected from the very population which the selection is targeting. However, selected breeding populations often have depleted genetic variation with small population sizes, resulting in low power in detecting useful QTLs. On the other hand, if selection is effective, loci controlling the selected trait will deviate from the expected Mendelian segregation ratio. In this study, we proposed to detect QTLs in selected breeding populations via the detection of marker segregation distortion in either a single population or multiple populations using the same selection scheme. Simulation studies showed that QTL can be detected in strong selected populations with selected population sizes as small as 25 plants. We applied the new method to detect QTLs in two breeding populations of rice selected for high grain yield. Seven QTLs were identified, four of which have been validated in advanced generations in a follow-up study. -

Pleiotropic Patterns of Quantitative Trait Loci for 70 Murine Skeletal Traits
Copyright Ó 2008 by the Genetics Society of America DOI: 10.1534/genetics.107.084434 Pleiotropic Patterns of Quantitative Trait Loci for 70 Murine Skeletal Traits Jane P. Kenney-Hunt,*,1 Bing Wang,* Elizabeth A. Norgard,* Gloria Fawcett,* Doug Falk,* L. Susan Pletscher,* Joseph P. Jarvis,* Charles Roseman,† Jason Wolf‡ and James M. Cheverud* *Department of Anatomy and Neurobiology, Washington University School of Medicine, St. Louis, Missouri 63110, †Department of Anthropology, University of Illinois, Urbana, Illinois 61801 and ‡Faculty of Life Sciences, University of Manchester, Manchester M13 9PT, United Kingdom Manuscript received November 11, 2007 Accepted for publication February 1, 2008 ABSTRACT Quantitative trait locus (QTL) studies of a skeletal trait or a few related skeletal components are becoming commonplace, but as yet there has been no investigation of pleiotropic patterns throughout the skeleton. We present a comprehensive survey of pleiotropic patterns affecting mouse skeletal morphology in an intercross of LG/J and SM/J inbred strains (N ¼ 1040), using QTL analysis on 70 skeletal traits. We identify 798 single- trait QTL, coalescing to 105 loci that affect on average 7–8 traits each. The number of traits affected per locus ranges from only 1 trait to 30 traits. Individual traits average 11 QTL each, ranging from 4 to 20. Skeletal traits are affected by many, small-effect loci. Significant additive genotypic values average 0.23 standard deviation (SD) units. Fifty percent of loci show codominance with heterozygotes having intermediate phenotypic values. When dominance does occur, the LG/J allele tends to be dominant to the SM/J allele (30% vs. -

To Clone Or Not to Clone Plant Qtls: Present and Future Challenges
Review TRENDS in Plant Science Vol.10 No.6 June 2005 To clone or not to clone plant QTLs: present and future challenges Silvio Salvi and Roberto Tuberosa Department of Agroenvironmental Science and Technology, University of Bologna, Viale Fanin, 44, 40127 Bologna, Italy Recent technical advancements and refinement of studies completed to date indicate an L-shaped distri- analytical methods have enabled the loci (quantitative bution of QTL effects (i.e. most QTLs have a small effect trait loci, QTLs) responsible for the genetic control of and only a few show a strong effect) [5], thus enabling quantitative traits to be dissected molecularly. To date, the identification of QTLs with a major effect on the most plant QTLs have been cloned using a positional phenotype. cloning approach following identification in experi- Currently, QTL mapping is a standard procedure in mental crosses. In some cases, an association between quantitative genetics [6]. QTL mapping usually begins sequence variation at a candidate gene and a phenotype with the collection of genotypic (based on molecular has been established by analysing existing genetic markers) and phenotypic data from a segregating popu- accessions. These strategies can be refined using lation, followed by statistical analysis to reveal all possible appropriate genetic materials and the latest develop- marker loci where allelic variation correlates with the ments in genomics platforms. We foresee that although phenotype. Because this procedure only allows for an QTL analysis and cloning addressing naturally occurring approximate mapping of the QTL, it is usually referred to genetic variation should shed light on mechanisms of as primary (or coarse) QTL mapping. -

100 Years of Quantitative Genetics Theory and Its Applications: Celebrating the Centenary of Fisher 1918”
Report on the meeting “100 years of quantitative genetics theory and its applications: celebrating the centenary of Fisher 1918” October 9, 2018 Wolfson Hall, Royal College of Surgeons, Nicolson St., Edinburgh EH8 9DW Sponsored by The Fisher Memorial Trust, the Genetics Society, the Galton Institute, the London Mathematical Society and the Royal Statistical Society Jessica G. King Institute of Evolutionary Biology, School of Biological Sciences, University of Edinburgh Ronald A. Fisher’s 1918 paper, entitled “The correlation between relatives on the supposition of Mendelian inheritance” and published in the Transactions of the Royal Society of Edinburgh, set the foundations for the study of the genetics of quantitative traits. 100 years later, we celebrate Fisher’s contribution and reflect on the advances made since this classical paper first emerged. Context Prior to R.A. Fisher’s famous contribution, the genetic basis of evolutionary change was vigorously disputed between biometricians and Mendelians. In support of Darwin’s theory of evolution by natural selection, biometricians believed evolution to be a continuous process, having developed much of modern statistical methods such as regression and correlation to describe the inheritance of biometric (continuous or quantitative) traits. After the rediscovery of Mendel’s work on inheritance, the Mendelians argued against these views by vehemently supporting discontinuous evolution via Mendelian (discontinuous) traits controlled by the segregation of major genetic factors. The first attempts to reconcile the two opposing schools of thought were made independently by George Udny Yule in 1902 and Wilhelm Weinberg in 1910, whose studies were largely overlooked by both biometricians and Mendelians, blinded by the ongoing conflict. -

Nature, Nurture and Egalitarian Policy: What Can We Learn from Molecular Genetics?
IZA DP No. 4585 Nature, Nurture and Egalitarian Policy: What Can We Learn from Molecular Genetics? Petter Lundborg Anders Stenberg November 2009 DISCUSSION PAPER SERIES Forschungsinstitut zur Zukunft der Arbeit Institute for the Study of Labor Nature, Nurture and Egalitarian Policy: What Can We Learn from Molecular Genetics? Petter Lundborg VU University Amsterdam, Tinbergen Institute, Lund University and IZA Anders Stenberg SOFI, Stockholm University Discussion Paper No. 4585 November 2009 IZA P.O. Box 7240 53072 Bonn Germany Phone: +49-228-3894-0 Fax: +49-228-3894-180 E-mail: [email protected] Any opinions expressed here are those of the author(s) and not those of IZA. Research published in this series may include views on policy, but the institute itself takes no institutional policy positions. The Institute for the Study of Labor (IZA) in Bonn is a local and virtual international research center and a place of communication between science, politics and business. IZA is an independent nonprofit organization supported by Deutsche Post Foundation. The center is associated with the University of Bonn and offers a stimulating research environment through its international network, workshops and conferences, data service, project support, research visits and doctoral program. IZA engages in (i) original and internationally competitive research in all fields of labor economics, (ii) development of policy concepts, and (iii) dissemination of research results and concepts to the interested public. IZA Discussion Papers often represent preliminary work and are circulated to encourage discussion. Citation of such a paper should account for its provisional character. A revised version may be available directly from the author.