DOCSLIB.ORG

Novel Statistical Methods in Quantitative Genetics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Novel Statistical Methods in Quantitative Genetics Dedicated to my family in Shiyan, Hubei, China, . especially to my grandparents for their indispensable guidance all these years. List of papers This thesis is based on the following papers, which are referred to in the text by their Roman numerals. I Rönnegård, L., Shen, X. and Alam, M. (2010). hglm: a package for fitting hierarchical generalized linear models. The R Journal. 2(2):20-28. II Shen, X., Rönnegård, L. and Carlborg, Ö. (2011). How to deal with genotype uncertainty in variance component quantitative trait loci analyses. Genetics Re- search, Cambridge. 93(5):333-342. III Shen, X., Rönnegård, L. and Carlborg, Ö. (2011). Hierarchical likelihood opens a new way of estimating genetic values using genome-wide dense marker maps. BMC Proceedings. 5(Suppl 3):S14. IV Nelson, R., Shen, X. and Carlborg, Ö. (2011). qtl.outbred: interfacing out- bred line cross data with the R/qtl mapping software. BMC Research Notes. 4:154. V Shen, X., Pettersson, M., Rönnegård, L. and Carlborg, Ö. (2012). Inheritance beyond plain heritability: variance controlling genes in Arabidopsis thaliana. Submitted. VI Shen, X., Alam, M., Fikse, F. and Rönnegård, L. (2012). Fast generalized ridge regression for models including heteroscedastic effects in quantitative genetics. Manuscript. Reprints were made with permission from the publishers. Contents Part I: Introduction .............................................................................................. 11 1 Background & Aims ...................................................................................... 12 2 Discovering Genetic Architecture .................................................................. 14 2.1 Single-predictor analysis ..................................................................... 15 2.1.1 QTL analysis ......................................................................... 15 2.1.2 Genome-wide association study ............................................. 19 2.2 Multiple-predictor analysis .................................................................. 22 2.2.1 Polygenic effects estimation ................................................... 22 2.2.2 Interaction effects and variance heterogeneity ......................... 23 3 Predictive Modeling ....................................................................................... 27 Part II: Summary of Papers .................................................................................. 31 4 Implementing Hierarchical Generalized Linear Models (Paper I) .................... 32 5 Quantitative Trait Loci Interval Mapping ........................................................ 36 5.1 Variance component QTL model (Paper II) .......................................... 36 5.2 QTL regression model (Paper IV) ........................................................ 39 6 Fitting The Entire Genome ............................................................................. 40 6.1 Double HGLM (Paper III) ................................................................... 41 6.2 Heteroscedastic effects model (Paper VI) ............................................. 45 7 Beyond Plain Heritability: Variance-Controlling Genes (Paper V) .................. 48 Part III: Discussion & Conclusion ........................................................................ 53 8 Discussion ..................................................................................................... 54 8.1 Heritability: How much can we explain? ............................................. 54 8.2 New data types: How to integrate information? .................................... 56 8.3 Future development ............................................................................. 56 9 Conclusion .................................................................................................... 57 References .......................................................................................................... 61 Nomenclature AMD age-related macular degeneration ANOVA analysis of variance BLUP best linear unbiased predictor BMI body mass index cM centi-Morgan CRP C-reactive protein DHGLM double HGLM DNA deoxyribonucleic acid EBV estimated breeding value EM expectation-maximization FPR false positive rate GBLUP genomic BLUP GC genomic control GEBV genomic EBV GLM generalized linear model GLMM generalized linear mixed model GM genetically modified GO gene ontology GRAMMAR genome-wide rapid association using mixed model and regression GWAS genome-wide association study h-likelihood hierarchical likelihood HDL high-density lipoprotein HEM heteroscedastic effects model HGLM hierarchical generalized linear model HMM hidden Markov model IBD identity-by-descent IBS identity-by-state IWLS iterative weighted least squares LAF low-variance allele frequency LASSO least absolute shrinkage and selection operator LD linkage disequilibrium LM (normal) linear model (regression) LMM (normal) linear mixed model LOD logarithm of odds LRT likelihood ratio test MCMC Markov chain Monte Carlo 9 ML maximum likelihood MME mixed model equations PCA principle component analysis PQL penalized quasi-likelihood QTL quantitative trait locus/loci REML restricted maximum likelihood RR ridge regression SNP single nucleotide polymorphism SSR simple sequence repeat TBV true breeding value VC variance component vGWAS variance-heterogeneity GWAS vQTL variance-controlling QTL 10 PART I: INTRODUCTION 1. Background & Aims “We have now entered a new era of large-scale genetics unthinkable even a few years ago.” —— Peter Donnelly T was by investigating genetics that modern statistics was founded. GALTON (1886) I regressed the mid-parents’ heights on their children’s, which opened the gate to a science that filters out knowledge from chaos, i.e. statistics. FISHER (1918) studied correlation in Mendelian inheritance, which brought analysis of variance (ANOVA) into the field of probability theory and statistics. Genetics and statistics seem to be destined to meet each other due to different kinds of uncertainty in heredity that we still do not understand. Another classic example that genetics drove statistics to develop is the mixed model, a.k.a. random effects model or variance component model, which is the basis of most studies described in this thesis. Millions of poultry and livestock are evaluated ev- ery year via what are called Henderson’s mixed model equations (HENDERSON 1953, 1984; VAN VLECK 1998). Although criticized by some statisticians at the beginning that one should not calculate point estimates for random effects, the mixed model equations have been proved to give so-called best linear unbiased prediction, or BLUP (ROBINSON 1991). It is actually a general method for estimating random effects and dealing with correlated observations, which has great prediction power. Nowadays, not only in animal breeding and genetics, BLUP has also been widely applied in tech- nology and social sciences. The goal of statistical genetics is to analyze genetic data and give explanations of how the variation in the observed traits are affected by genetic variation. Since one of the essential attributes of statistical analysis in genetics is the relatedness among individuals, the key to achieve such a goal is to trace inheritance among individu- als. Before molecular markers were applied, inheritance could be traced only through kinship constructed from a pedigree structure. Such a kinship can be used to model inheritance in e.g. farm animals and human families. After molecular markers became available, statistical tools for genetic analyses started to have more diversity. Being able to trace inheritance of a specific segment of DNA, statistical tests can help identify genes or quantitative trait loci (QTL) that regulate quantitative traits. Analyzing most of the traits are difficult because of the complexity of genetic architecture underly- ing the traits. Due to the fast development of genotyping and sequencing techniques, statistical analyses for different genetics problems now start using the same kind of 12 high-dimensional genomic data. Both QTL interval mapping and genome-wide asso- ciation studies (GWAS) utilize the genetic information carried by high-density SNPs to identify major genetic loci that affect complex traits. Also using the same high- density SNPs, breeders reconstruct the kinship of the studied individuals directly by comparing their genomes and give better evaluations of the animals, i.e. GBLUP. It is now an exciting moment in quantitative genetics that a consistent type of high- dimensional data can be used to explain so many problems regarding inheritance that we are interested in. The aim of this thesis is to develop new statistical tools in both QTL analysis and genomic evaluation. Most of the proposed statistical methods focus on modeling ge- netic variance, especially using random effects models. Properly modeling genetic variance could help us better understand the genetic contribution to various types of complex traits. The thesis contains three parts: the introduction, the summary of papers, and the discussion. Part I briefly introduces the background knowledge related to my research. Chapter 2 introduces the basics of several statistical tools for gene mapping, including QTL analysis, GWAS, whole-genome shrinkage estimation methods, and interactions with the connection to the idea of variance-controlling genes. Chapter 3 introduces the use of genomic dense markers in prediction and discusses model selection. Part II summarizes the papers that this
Load more

Recommended publications
  • Lineage-Specific Mapping of Quantitative Trait Loci
    Heredity (2013) 111, 106–113 & 2013 Macmillan Publishers Limited All rights reserved 0018-067X/13 www.nature.com/hdy ORIGINAL ARTICLE Lineage-specific mapping of quantitative trait loci C Chen1 and K Ritland We present an approach for quantitative trait locus (QTL) mapping, termed as ‘lineage-specific QTL mapping’, for inferring allelic changes of QTL evolution along with branches in a phylogeny. We describe and analyze the simplest case: by adding a third taxon into the normal procedure of QTL mapping between pairs of taxa, such inferences can be made along lineages to a presumed common ancestor. Although comparisons of QTL maps among species can identify homology of QTLs by apparent co- location, lineage-specific mapping of QTL can classify homology into (1) orthology (shared origin of QTL) versus (2) paralogy (independent origin of QTL within resolution of map distance). In this light, we present a graphical method that identifies six modes of QTL evolution in a three taxon comparison. We then apply our model to map lineage-specific QTLs for inbreeding among three taxa of yellow monkey-flower: Mimulus guttatus and two inbreeders M. platycalyx and M. micranthus, but critically assuming outcrossing was the ancestral state. The two most common modes of homology across traits were orthologous (shared ancestry of mutation for QTL alleles). The outbreeder M. guttatus had the fewest lineage-specific QTL, in accordance with the presumed ancestry of outbreeding. Extensions of lineage-specific QTL mapping to other types of data and crosses, and to inference of ancestral QTL state, are discussed. Heredity (2013) 111, 106–113; doi:10.1038/hdy.2013.24; published online 24 April 2013 Keywords: Quantitative trait locus mapping; evolution of mating systems; Mimulus INTRODUCTION common ancestor of these two taxa, back to the common ancestor of Knowledge of the genetic architecture of complex traits can offer all three taxa and forwards again to the third taxon.
    [Show full text]
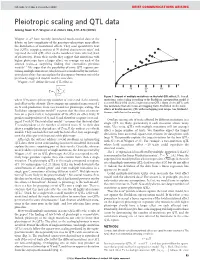
  • Pleiotropic Scaling and QTL Data Arising From: G
    NATURE | Vol 456 | 4 December 2008 BRIEF COMMUNICATIONS ARISING Pleiotropic scaling and QTL data Arising from: G. P. Wagner et al. Nature 452, 470–473 (2008) Wagner et al.1 have recently introduced much-needed data to the debate on how complexity of the genotype–phenotype map affects the distribution of mutational effects. They used quantitative trait loci (QTLs) mapping analysis of 70 skeletal characters in mice2 and regressed the total QTL effect on the number of traits affected (level of pleiotropy). From their results they suggest that mutations with higher pleiotropy have a larger effect, on average, on each of the T affected traits—a surprising finding that contradicts previous models3–7. We argue that the possibility of some QTL regions con- taining multiple mutations, which was not considered by the authors, introduces a bias that can explain the discrepancy between one of the previously suggested models and the new data. Wagner et al.1 define the total QTL effect as vffiffiffiffiffiffiffiffiffiffiffiffiffi u uXN 10 20 30 ~t 2 T Ai N i~1 Figure 1 | Impact of multiple mutations on the total QTL effect, T. For all where N measures pleiotropy (number of traits) and Ai the normal- mutations, strict scaling according to the Euclidean superposition model is ized effect on the ith trait. They compare an empirical regression of T assumed. Black filled circles, single-mutation QTLs. Open circles, QTLs with on N with predictions from two models for pleiotropic scaling. The two mutations that affect non-overlapping traits. Red filled circles, total Euclidean superposition model3,4 assumes that the effect of a muta- effects of double-mutant QTL with overlapping trait ranges (see Methods).
    [Show full text]
  • 1 ROBERT PLOMIN on Behavioral Genetics Genetic Links Common
    Genetic links • Background – Why has educational psychology ben so slow ROBERT PLOMIN to accept genetics? on Behavioral Genetics • Beyond nature vs. nurture – 3 findings from genetic research with far- reaching implications for education: October, 2004 The nature of nurture The abnormal is normal Generalist genes • Molecular Genetics Quantitative genetics: twin and adoption studies Common medical disorders Identical twins Fraternal twins (monozygotic, MZ) (dizygotic, DZ) 1 Twin concordances in TEDS at 7 years Twins Early Development Study (TEDS) for low reading and maths Perceptions of nature/nurture: % parents (N=1340) and teachers Beyond nature vs. nurture: (N=667) indicating that genes are at least as important as environment (Walker & Plomin, Ed. Psych., in press) The nature of nurture • Genetic influence on experience • Genotype-environment correlation – Children’s genetic propensities are correlated with their experiences passive evocative active 2 Beyond nature vs. nurture: Genotype-environment correlation The nature of nurture • Passive • Genotype-environment correlation – e.g., family background (SES) and school – Children’s genetic propensities are correlated with achievement their experiences passive • Evocative evocative – Children evoke experiences for genetic reasons Active • Active • Molecular genetics – Children actively create environments that foster – Find genes associated with learning experiences their genetic propensities Beyond nature vs. nurture: The one-gene one-disability (OGOD) model The abnormal is normal • Common learning disabilities are the quantitative extreme of the same genetic and environmental factors responsible for normal variation in learning abilities. • There are no common learning disabilities, just the extremes of normal variation. 3 OGOD (rare) and QTL (common) disorders The quantitative trait locus (QTL) model Beyond nature vs.
    [Show full text]
  • Special Issues on Advances in Quantitative Genetics: Introduction
    Heredity (2014) 112, 1–3 & 2014 Macmillan Publishers Limited All rights reserved 0018-067X/14 www.nature.com/hdy EDITORIAL Special issues on advances in quantitative genetics: introduction Heredity (2014) 112, 1–3; doi:10.1038/hdy.2013.115 Fisher’s (1918) classic paper on the inheritance of complex traits not While much of the focus was on standard biometrical applications only founded the field of quantitative genetics, but also coined the (for example, variance components), hints of things to come were term variance and introduced the powerful statistical method of foreshadowed by papers on the relevance of molecular biology to analysis of variance. This was a watershed paper, reconciling the breeding and applications of mixed models (models including both Mendelian’s discrete and saltatorial view of trait evolution with the fixed and random effects, for example, BLUP and REML). Much of gradual and continuous view of Darwin’s followers, the biometricians the emphasis was on breeding or laboratory populations. A decade (Provine, 1971). This fusion of Mendelian genetics with Darwinian later, the second ICQG held at Raleigh, North Carolina in 1987 natural selection was the start of the modern evolutionary synthesis. (Weir et al., 1988), reflected explosive growth in new tools (low- Fisher’s paper also marked a critical point in modern statistics, and density molecular markers for early quantitative trait locus (QTL) this synergism between the development of new statistical methods mapping), a continued expansion of the importance of mixed-model and the ever-increasing complexity of genetic/genomic data sets methodology for complex estimation issues, and a growing fusion of continues to this day.
    [Show full text]
  • New Strategies and Tools in Quantitative Genetics: How to Go from the Phenotype to the Genotype
    PP68CH16-Loudet ARI 6 April 2017 9:43 ANNUAL REVIEWS Further Click here to view this article's online features: • Download figures as PPT slides • Navigate linked references • Download citations New Strategies and Tools in • Explore related articles • Search keywords Quantitative Genetics: How to Go from the Phenotype to the Genotype Christos Bazakos, Mathieu Hanemian, Charlotte Trontin, JoseM.Jim´ enez-G´ omez,´ and Olivier Loudet Institut Jean-Pierre Bourgin, INRA, AgroParisTech, CNRS, Universite´ Paris-Saclay, 78026 Versailles Cedex, France; email: [email protected] Annu. Rev. Plant Biol. 2017. 68:435–55 Keywords First published online as a Review in Advance on genetic architecture, QTL, RIL, GWAS, phenotype February 6, 2017 The Annual Review of Plant Biology is online at Abstract plant.annualreviews.org Quantitative genetics has a long history in plants: It has been used to study https://doi.org/10.1146/annurev-arplant-042916- specific biological processes, identify the factors important for trait evolu- 040820 Annu. Rev. Plant Biol. 2017.68:435-455. Downloaded from www.annualreviews.org tion, and breed new crop varieties. These classical approaches to quantitative Copyright c 2017 by Annual Reviews. trait locus mapping have naturally improved with technology. In this review, All rights reserved we show how quantitative genetics has evolved recently in plants and how new developments in phenotyping, population generation, sequencing, gene Access provided by INRA Institut National de la Recherche Agronomique on 05/05/17. For personal use only. manipulation, and statistics are rejuvenating both the classical linkage map- ping approaches (for example, through nested association mapping) as well as the more recently developed genome-wide association studies.
    [Show full text]
  • Epigenome-Wide Study Identified Methylation Sites Associated With
    nutrients Article Epigenome-Wide Study Identified Methylation Sites Associated with the Risk of Obesity Majid Nikpay 1,*, Sepehr Ravati 2, Robert Dent 3 and Ruth McPherson 1,4,* 1 Ruddy Canadian Cardiovascular Genetics Centre, University of Ottawa Heart Institute, 40 Ruskin St–H4208, Ottawa, ON K1Y 4W7, Canada 2 Plastenor Technologies Company, Montreal, QC H2P 2G4, Canada; [email protected] 3 Department of Medicine, Division of Endocrinology, University of Ottawa, the Ottawa Hospital, Ottawa, ON K1Y 4E9, Canada; [email protected] 4 Atherogenomics Laboratory, University of Ottawa Heart Institute, Ottawa, ON K1Y 4W7, Canada * Correspondence: [email protected] (M.N.); [email protected] (R.M.) Abstract: Here, we performed a genome-wide search for methylation sites that contribute to the risk of obesity. We integrated methylation quantitative trait locus (mQTL) data with BMI GWAS information through a SNP-based multiomics approach to identify genomic regions where mQTLs for a methylation site co-localize with obesity risk SNPs. We then tested whether the identified site contributed to BMI through Mendelian randomization. We identified multiple methylation sites causally contributing to the risk of obesity. We validated these findings through a replication stage. By integrating expression quantitative trait locus (eQTL) data, we noted that lower methylation at cg21178254 site upstream of CCNL1 contributes to obesity by increasing the expression of this gene. Higher methylation at cg02814054 increases the risk of obesity by lowering the expression of MAST3, whereas lower methylation at cg06028605 contributes to obesity by decreasing the expression of SLC5A11. Finally, we noted that rare variants within 2p23.3 impact obesity by making the cg01884057 Citation: Nikpay, M.; Ravati, S.; Dent, R.; McPherson, R.
    [Show full text]
  • Quantitative Genetics of Gene Expression and Methylation in the Chicken
    Andrey Höglund Linköping Studies In Science and Technology Dissertation No. 2097 FACULTY OF SCIENCE AND ENGINEERING Linköping Studies in Science and Technology, Dissertation No. 2097, 2020 Quantitative genetics Department of Physics, Chemistry and Biology Linköping University SE-581 83 Linköping, Sweden of gene expression Quantitative genetics of gene expression and methylation the in chicken www.liu.se and methylation in the chicken Andrey Höglund 2020 Linköping studies in science and technology, Dissertation No. 2097 Quantitative genetics of gene expression and methylation in the chicken Andrey Höglund IFM Biology Department of Physics, Chemistry and Biology Linköping University, SE-581 83, Linköping, Sweden Linköping 2020 Cover picture: Hanne Løvlie Cover illustration: Jan Sulocki During the course of the research underlying this thesis, Andrey Höglund was enrolled in Forum Scientium, a multidisciplinary doctoral program at Linköping University, Sweden. Linköping studies in science and technology, Dissertation No. 2097 Quantitative genetics of gene expression and methylation in the chicken Andrey Höglund ISSN: 0345-7524 ISBN: 978-91-7929-789-3 Printed in Sweden by LiU-tryck, Linköping, 2020 Abstract In quantitative genetics the relationship between genetic and phenotypic variation is investigated. The identification of these variants can bring improvements to selective breeding, allow for transgenic techniques to be applied in agricultural settings and assess the risk of polygenic diseases. To locate these variants, a linkage-based quantitative trait locus (QTL) approach can be applied. In this thesis, a chicken intercross population between wild and domestic birds have been used for QTL mapping of phenotypes such as comb, body and brain size, bone density and anxiety behaviour.
    [Show full text]
  • QUANTITATIVE TRAIT LOCUS ANALYSIS: in Several Variants (I.E., Alleles)
    TECHNOLOGIES FROM THE FIELD QUANTITATIVE TRAIT LOCUS ANALYSIS: in several variants (i.e., alleles). QTL analysis allows one MULTIPLE CROSS AND HETEROGENEOUS to map, with some precision, the genomic position of STOCK MAPPING these alleles. For many researchers in the alcohol field, the break­ Robert Hitzemann, Ph.D.; John K. Belknap, Ph.D.; through with respect to the genetic determination of alcohol- and Shannon K. McWeeney, Ph.D. related behaviors occurred when Plomin and colleagues (1991) made the seminal observation that a specific panel of RI mice (i.e., the BXD panel) could be used to identify KEY WORDS: Genetic theory of alcohol and other drug use; genetic the physical location of (i.e., to map) QTLs for behavioral factors; environmental factors; behavioral phenotype; behavioral phenotypes. Because the phenotypes of the different strains trait; quantitative trait gene (QTG); inbred animal strains; in this panel had been determined for many alcohol- recombinant inbred (RI) mouse strains; quantitative traits; related traits, researchers could readily apply the strategy quantitative trait locus (QTL) mapping; multiple cross mapping of RI–QTL mapping (Gora-Maslak et al. 1991). Although (MCM); heterogeneous stock (HS) mapping; microsatellite investigators recognized early on that this panel was not mapping; animal models extensive enough to answer all questions, the emerging data illustrated the rich genetic complexity of alcohol- related phenotypes (Belknap 1992; Plomin and McClearn ntil well into the 1990s, both preclinical and clinical 1993). research focused on finding “the” gene for human The next advance came with the development of diseases, including alcoholism. This focus was rein­ U microsatellite maps (Dietrich et al.
    [Show full text]
  • An Introduction to Quantitative Genetics I Heather a Lawson Advanced Genetics Spring2018 Outline
    An Introduction to Quantitative Genetics I Heather A Lawson Advanced Genetics Spring2018 Outline • What is Quantitative Genetics? • Genotypic Values and Genetic Effects • Heritability • Linkage Disequilibrium and Genome-Wide Association Quantitative Genetics • The theory of the statistical relationship between genotypic variation and phenotypic variation. 1. What is the cause of phenotypic variation in natural populations? 2. What is the genetic architecture and molecular basis of phenotypic variation in natural populations? • Genotype • The genetic constitution of an organism or cell; also refers to the specific set of alleles inherited at a locus • Phenotype • Any measureable characteristic of an individual, such as height, arm length, test score, hair color, disease status, migration of proteins or DNA in a gel, etc. Nature Versus Nurture • Is a phenotype the result of genes or the environment? • False dichotomy • If NATURE: my genes made me do it! • If NURTURE: my mother made me do it! • The features of an organisms are due to an interaction of the individual’s genotype and environment Genetic Architecture: “sum” of the genetic effects upon a phenotype, including additive,dominance and parent-of-origin effects of several genes, pleiotropy and epistasis Different genetic architectures Different effects on the phenotype Types of Traits • Monogenic traits (rare) • Discrete binary characters • Modified by genetic and environmental background • Polygenic traits (common) • Discrete (e.g. bristle number on flies) or continuous (human height)
    [Show full text]
  • Article the Power to Detect Quantitative Trait Loci Using
    The Power to Detect Quantitative Trait Loci Using Resequenced, Experimentally Evolved Populations of Diploid, Sexual Organisms James G. Baldwin-Brown,*,1 Anthony D. Long,1 and Kevin R. Thornton1 1Department of Ecology and Evolutionary Biology, University of California, Irvine *Corresponding author: E-mail: [email protected]. Associate editor: John Parsch Abstract A novel approach for dissecting complex traits is to experimentally evolve laboratory populations under a controlled environment shift, resequence the resulting populations, and identify single nucleotide polymorphisms (SNPs) and/or genomic regions highly diverged in allele frequency. To better understand the power and localization ability of such an evolve and resequence (E&R) approach, we carried out forward-in-time population genetics simulations of 1 Mb genomic regions under a large combination of experimental conditions, then attempted to detect significantly diverged SNPs. Our analysis indicates that the ability to detect differentiation between populations is primarily affected by selection coef- ficient, population size, number of replicate populations, and number of founding haplotypes. We estimate that E&R studies can detect and localize causative sites with 80% success or greater when the number of founder haplotypes is over 500, experimental populations are replicated at least 25-fold, population size is at least 1,000 diploid individuals, and the selection coefficient on the locus of interest is at least 0.1. More achievable experimental designs (less replicated, fewer founder haplotypes, smaller effective population size, and smaller selection coefficients) can have power of greater than 50% to identify a handful of SNPs of which one is likely causative. Similarly, in cases where s 0.2, less demanding experimental designs can yield high power.
    [Show full text]
  • Quantitative Genetics and Heritability of Growth-Related Traits in Hybrid Striped Bass (Morone Chrysops ♀×Morone Saxatilis ♂)
    Aquaculture 261 (2006) 535–545 www.elsevier.com/locate/aqua-online Quantitative genetics and heritability of growth-related traits in hybrid striped bass (Morone chrysops ♀×Morone saxatilis ♂) Xiaoxue Wang a, Kirstin E. Ross b, Eric Saillant a, ⁎ Delbert M. Gatlin III a, John R. Gold a, a Center for Biosystematics and Biodiversity, Department of Wildlife and Fisheries Sciences, Texas A&M University, College Station, TX 77843-2258, USA b Department of Environmental Health, Flinders University, Adelaide, SA, 5001, Australia Received 30 November 2005; received in revised form 19 July 2006; accepted 21 July 2006 Abstract Commercially farmed, hybrid striped bass – female white bass (Morone chrysops) crossed with male striped bass (Morone saxatilis) – represent a rapidly growing industry in the United States. Expanded production of hybrid striped bass, however, is limited because of uncontrolled variation in performance of fish derived from undomesticated broodstock. A 10×10 factorial mating design was employed to examine genetic effects and heritability of growth-related traits based on dam half-sib and sire half- sib families. A total of 881 offspring were raised in a common environment and body weight and length were recorded at three different times post-fertilization; parentage of each fish was inferred from genotypes at 10 nuclear-encoded microsatellites. Dam and sire effects on juvenile growth (weight and length) and growth rate were significant, whereas dam by sire interaction effect was not. The dam and sire components of variance for weight and length (at age) and growth rate were estimated using a Restricted Maximum Likelihood algorithm. Estimates of broad-sense heritability of weight, using a family-mean basis, ranged from 0.67± 0.17 to 0.85±0.07 for dams; estimates for sires ranged from 0.43±0.20 to 0.77±0.10.
    [Show full text]
  • Contribution and Perspectives of Quantitative Genetics to Plant Breeding in Brazil
    Contribution and perspectives of quantitative genetics to plant breeding in Brazil Crop Breeding and Applied Biotechnology S2: 7-14, 2012 Brazilian Society of Plant Breeding. Printed in Brazil Contribution and perspectives of quantitative genetics to plant breeding in Brazil Roland Vencovsky1, Magno Antonio Patto Ramalho2* and Fernando Henrique Ribeiro Barrozo Toledo1 Received 15 September 2012 Accepted 03 October 2012 Abstract – The purpose of this article is to show how quantitative genetics has contributed to the huge genetic progress obtained in plant breeding in Brazil in the last forty years. The information obtained through quantitative genetics has given Brazilian breeders the possibility of responding to innumerable questions in their work in a much more informative way, such as the use or not of hybrid cultivars, which segregating population to use, which breeding method to employ, alternatives for improving the efficiency of selec- tion programs, and how to handle the data of progeny and/or cultivars evaluations to identify the most stable ones and thus improve recommendations. Key words: Genetic parameters, genotype by environment interaction, hybrid cultivars, stability and adaptability. INTRODUCTION Therefore, this article was written up with the purpose of commenting some of the innumerable aspects of quantitative Plant breeding has been conceptualized in different genetics in Brazil that contributed to decision-making of manners throughout its history. In the concept proposed by breeders, creating good managers and, above all, showing Kempthorne (1957) “plant breeding is applied quantitative that in recent decades, many decisions of Brazilian breeders genetics.” Considering that he was a biometrician, it is easy have been based on knowledge from quantitative genetics.
    [Show full text]