DOCSLIB.ORG

RM 2009 Calendar

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
RM 2009 Calendar Rudi Mathematici x4-8 204x3+25237646x2-34502914684x+17687247380985=0 Rudi Mathematici January 1 1 T (1803) Guglielmo LIBRI Carucci dalla Sommaja USAMO 1999 – Pr. 1 (1878) Agner Krarup ERLANG (1894) Satyendranath BOSE Some checkers placed on an n× n (1912) Boris GNEDENKO checkerboard satisfy the following conditions: (1822) Rudolf Julius Emmanuel CLAUSIUS 2 F (1905) Lev Genrichovich SHNIRELMAN (a) every square that does not contain a (1938) Anatoly SAMOILENKO checker shares a side with one that 3 S (1917) Yuri Alexeievich MITROPOLSHY does; 4 S (1643) Isaac NEWTON (b) given any pair of squares that contain checkers, there is a sequence of 2 5 M (1838) Marie Ennemond Camille JORDAN (1871) Federigo ENRIQUES squares containing checkers, starting (1871) Gino FANO and ending with the given squares, such that every two consecutive 6 T (1807) Jozeph Mitza PETZVAL (1841) Rudolf STURM squares of the sequence share a side. 7 W (1871) Felix Edouard Justin Emile BOREL ()2 − (1907) Raymond Edward Alan Christopher PALEY Prove that at least n 2 / 3 checkers have (1888) Richard COURANT 8 T been placed on the board. (1924) Paul Moritz COHN (1942) Stephen William HAWKING Mathematics Terms (1864) Vladimir Adreievich STELKOV 9 F CLEARLY: I don’t want to write down all the (1875) Issai SCHUR 10 S “in- between” steps. (1905) Ruth MOUFANG (1545) Guidobaldo DEL MONTE TRIVIAL: If I have to show you how to do 11 S (1707) Vincenzo RICCATI this, you’re in the wrong class. (1734) Achille Pierre Dionis DU SEJOUR Calculus! 3 12 M (1906) Kurt August HIRSCH (1864) Wilhelm Karl Werner Otto Fritz Franz WIEN 2 13 T They chose an ε that was so small that ε (1876) Luther Pfahler EISENHART (1876) Erhard SCHMIDT was negative. (1902) Alfred TARSKI 14 W “The future science of government should be (1704) Johann CASTILLON 15 T called ‘la cybernetique’.” (1717) Mattew STEWART (1850) Sofia Vasilievna KOVALEVSKAJA Andrè Marie AMPERE 16 F (1801) Thomas KLAUSEN [Asked for a testimony to the fact that Emmy Noether was a great woman mathematician, 17 S (1847) Nikolay Egorovich ZUKOWSKY (1858) Gabriel KOENIGS he said:] “I can testify that she is a great 18 S (1856) Luigi BIANCHI mathematician, but that she is a woman, I (1880) Paul EHRENFEST cannot swear.” 4 19 M (1813) Rudolf Friedrich Alfred CLEBSCH (1879) Guido FUBINI Edmund LANDAU (1908) Aleksandr Gennadievich KUROS “Physics is becoming too difficult for the (1775) Andrè Marie AMPERE 20 T physicists.” (1895) Gabor SZEGO (1904) Renato CACCIOPPOLI David HILBERT 21 W (1846) Pieter Hendrik SCHOUTE “Father of Chemistry and Uncle of the Earl of (1915) Yuri Vladimirovich LINNIK Cork.” (1592) Pierre GASSENDI 22 T (1908) Lev Davidovich LANDAU Robert BOYLE [On his tombstone] (1840) Ernst ABBE 23 F “What I tell you three times is true.” (1862) David HILBERT Charles Lutwidge DOGSON 24 S (1891) Abram Samoilovitch BESICOVITCH (1914) Vladimir Petrovich POTAPOV “If you are afraid of something, measure it, (1627) Robert BOYLE 25 S and you will realize it is a mere triple.” (1736) Joseph-Louis LAGRANGE Renato CACCIOPPOLI (1843) Karl Herman Amandus SCHWARTZ 5 26 M (1799) Benoit Paul Emile CLAPEYRON 27 T (1832) Charles Lutwidge DODGSON (1701) Charles Marie de LA CONDAMINE 28 W (1892) Carlo Emilio BONFERRONI (1817) William FERREL 29 T (1888) Sidney CHAPMAN 30 F (1619) Michelangelo RICCI (1715) Giovanni Francesco FAGNANO dei Toschi 31 S (1841) Samuel LOYD (1896) Sofia Alexandrovna JANOWSKAJA www.rudimathematici.com Rudi Mathematici February 1 S (1900) John Charles BURKILL USAMO 1999 – Pr. 2 6 2 M (1522) Lodovico FERRARI Let ABCD be a cyclic quadrilateral. Prove (1893) Gaston Maurice JULIA 3 T that 4 W (1905) Eric Cristopher ZEEMAN AB − CD + AD − BC ≥ 2 AC − BD . 5 T (1757) Jean Marie Constant DUHAMEL (1612) Antoine ARNAULD 6 F (1695) Nicolaus (II) BERNOULLI Mathematic Terms 7 S (1877) Godfried Harold HARDY OBVIOUSLY: I hope you weren’t sleeping when (1883) Eric Temple BELL we discussed this earlier, because I refuse to 8 S (1700) Daniel BERNOULLI repeat it. (1875) Francis Ysidro EDGEWORTH 7 9 M (1775) Farkas Wolfgang BOLYAI RECALL: I shouldn’t have to tell you this, but (1907) Harod Scott MacDonald COXETER for those of you who erase your memory tapes 10 T (1747) Aida YASUAKI after every test... 11 W (1800) William Henry Fox TALBOT Mathematical Psychology (1839) Josiah Willard GIBBS (1915) Richard Wesley HAMMING Zenophobia: the irrational fear of convergent 12 T (1914) Hanna CAEMMERER NEUMANN sequences. 13 F (1805) Johann Peter Gustav Lejeune DIRICHLET “Common sense is not really so common.” 14 S (1468) Johann WERNER Antoine ARNAULD (1849) Hermann HANKEL (1896) Edward Artur MILNE “Technical skill is mastery of complexity while 15 S (1564) Galileo GALILEI creativity is mastery of simplicity.” (1861) Alfred North WHITEHEAD Eric Cristopher ZEEMAN (1946) Douglas HOFSTADTER 8 16 M (1822) Francis GALTON “Reductio ad absurdum, which Euclid loved so (1853) Georgorio RICCI-CURBASTRO much, is one of a mathematician’s finest (1903) Beniamino SEGRE weapons. It is a far finer gambit than any chess 17 T (1890) Sir Ronald Aymler FISHER play: a chess player may offer the sacrifice of a (1891) Adolf Abraham Halevi FRAENKEL pawn or even a piece, but a mathematician offers 18 W (1404) Leon Battista ALBERTI the game.” 19 T (1473) Nicolaus COPERNICUS Godfried HARDY 20 F (1844) Ludwig BOLTZMANN “It would be better for the true physics if there 21 S (1591) Girard DESARGUES were no mathematicians on earth.” (1915) Evgenni Michailovitch LIFSHITZ Daniel BERNOULLI 22 S (1903) Frank Plumpton RAMSEY “Epur si muove!” 9 23 M (1583) Jean-Baptiste MORIN (1951) Shigefumi MORI Galileo GALILEI 24 T (1871) Felix BERNSTEIN “Connaitre, decouvrir, communiquer... telle est 25 W (1827) Henry WATSON la destineè d’un savant.” Dominique ARAGO 26 T (1786) Dominique Francois Jean ARAGO “A mathematician will recognize Cauchy, Jacobi 27 F (1881) Luitzen Egbertus Jan BROUWER or Helmholtz after reading a few pages, just as a 28 S (1735) Alexandre Theophile VANDERMONDE musician recognize, from the first few bars, (1860) Herman HOLLERITH Mozart, Beethoven or Schubert.” Ludwig BOLTZMANN “Whenever you can, count.” Francis GALTON www.rudimathematici.com Rudi Mathematici March 1 S (1611) John PELL USAMO 1999 – Pr. 3 10 2 M (1836) Julius WEINGARTEN Let p > 2 be a prime and let a,b,c,d be 3 T (1838) George William HILL (1845) Georg CANTOR integers not divisible by p , such that 4 W (1822) Jules Antoine LISSAJUS (1512) Gerardus MERCATOR ⎧ra ⎫ ⎧rb⎫ ⎧rc⎫ ⎧rd ⎫ 5 T + + + = (1759) Benjamin GOMPERTZ ⎨ ⎬ ⎨ ⎬ ⎨ ⎬ ⎨ ⎬ 2 (1817) Angelo GENOCCHI ⎩ p ⎭ ⎩ p ⎭ ⎩ p ⎭ ⎩ p ⎭ 6 F (1866) Ettore BORTOLOTTI for any integer r not divisible by p . Prove (1792) William HERSCHEL 7 S that at least two of the numbers a+b, a+c, (1824) Delfino CODAZZI a+d,b+c, b+d, c+d 8 S (1851) George CHRYSTAL are divisible by p . 11 9 M (1818) Ferdinand JOACHIMSTHAL (1900) Howard Hathaway AIKEN (Note: {}x = x − ⎣⎦x denotes the fractional 10 T (1864) William Fogg OSGOOD (1811) Urbain Jean Joseph LE VERRIER part of x.) 11 W (1853) Salvatore PINCHERLE Mathematic Terms 12 T (1685) George BERKELEY (1824) Gustav Robert KIRKHHOFF WLOG (Without Loss Of Generality): I’m not (1859) Ernesto CESARO about to do all the possible cases, so I’ll do one 13 F (1861) Jules Joseph DRACH and let you figure out the rest. (1957) Rudy D’ALEMBERT IT CAN EASILY BE SHOWN: Even you, in 14 S (1864) Jozef KURSCHAK (1879) Albert EINSTEIN your finite wisdom, should be able to prove (1860) Walter Frank Raphael WELDON 15 S this without me holding your hand. (1868) Grace CHISOLM YOUNG 12 16 M (1750) Caroline HERSCHEL The Four Operations (1789) Georg Simon OHM Ambition, distraction, uglification and (1846) Magnus Gosta MITTAG-LEFFLER derision. (L. Carroll) 17 T (1876) Ernest Benjamin ESCLANGON (1897) Charles FOX “Common sense is nothing more than a deposit 18 W (1640) Philippe de LA HIRE of prejudices laid down in the mind before you (1690) Christian GOLDBACH (1796) Jacob STEINER reach eighteen.” 19 T (1862) Adolf KNESER Albert EINSTEIN (1910) Jacob WOLFOWITZ “We [he and Halmos] share a philosophy about (1840) Franz MERTENS 20 F linear algebra: we think basis-free, we write (1884) Philip FRANCK (1938) Sergi Petrovich NOVIKOV basis-free, but when the chips are down we (1768) Jean Baptiste Joseph FOURIER close the office door and compute with 21 S (1884) George David BIRKHOFF matrices like fury.” 22 S (1917) Irving KAPLANSKY Irving KAPLANSKY 13 23 M (1754) Georg Freiherr von VEGA “A Mathematician is a machine for turning (1882) Emmy Amalie NOETHER coffee into theorems.” (1897) John Lighton SYNGE Paul ERDOS 24 T (1809) Joseph LIOUVILLE (1948) Sun-Yung (Alice) CHANG “Perfect numbers (like perfect men) are very 25 W (1538) Christopher CLAUSIUS rare.” (1848) Konstantin ADREEV 26 T René DESCARTES (1913) Paul ERDOS “A mathematician is a person who can find 27 F (1857) Karl PEARSON analogies between theorems; a better 28 S (1749) Pierre Simon de LAPLACE mathematician is one who can see analogies 29 S (1825) Francesco FAÀ DI BRUNO between proofs and the best mathematician (1873) Tullio LEVI-CIVITA can notice analogies between theories. One can (1896) Wilhelm ACKERMAN imagine that the ultimate mathematician is 14 30 M (1892) Stefan BANACH one who can see analogies between analogies.” 31 T (1596) René DESCARTES Stefan BANACH www.rudimathematici.com Rudi Mathematici April (1640) Georg MOHR 1 W USAMO 1999 – Pr. 4 (1776) Marie-Sophie GERMAIN (1895) Alexander Craig AITKEN ()> Let a1 ,a2 ,K,an n 3 be real 2 T (1934) Paul Joseph COHEN (1835) John Howard Van AMRINGE numbers such that: 3 F (1892) Hans RADEMACHER + + + ≥ (1900) Albert Edward INGHAM a1 a2 K an n (1909) Stanislaw Marcin ULAM (1971) Alice RIDDLE And (1809) Benjamin PEIRCE 2 2 2 2 4 S + + + ≥ .
Load more

Recommended publications
  • Pursuit of Genius: Flexner, Einstein, and the Early Faculty at the Institute
    i i i i PURSUIT OF GENIUS i i i i i i i i PURSUIT OF GENIUS Flexner, Einstein,and the Early Faculty at the Institute for Advanced Study Steve Batterson Emory University A K Peters, Ltd. Natick, Massachusetts i i i i i i i i Editorial, Sales, and Customer Service Office A K Peters, Ltd. 5 Commonwealth Road, Suite 2C Natick, MA 01760 www.akpeters.com Copyright ⃝c 2006 by A K Peters, Ltd. All rights reserved. No part of the material protected by this copyright notice may be reproduced or utilized in any form, electronic or mechanical, including photocopy- ing, recording, or by any information storage and retrieval system, without written permission from the copyright owner. Library of Congress Cataloging-in-Publication Data Batterson, Steve, 1950– Pursuit of genius : Flexner, Einstein, and the early faculty at the Institute for Advanced Study / Steve Batterson. p. cm. Includes bibliographical references and index. ISBN 13: 978-1-56881-259-5 (alk. paper) ISBN 10: 1-56881-259-0 (alk. paper) 1. Mathematics–Study and teaching (Higher)–New Jersey–Princeton–History. 2. Institute for Advanced Study (Princeton, N.J.). School of Mathematics–History. 3. Institute for Advanced Study (Princeton, N.J.). School of Mathematics–Faculty. I Title. QA13.5.N383 I583 2006 510.7’0749652--dc22 2005057416 Cover Photographs: Front cover: Clockwise from upper left: Hermann Weyl (1930s, cour- tesy of Nina Weyl), James Alexander (from the Archives of the Institute for Advanced Study), Marston Morse (photo courtesy of the American Mathematical Society), Albert Einstein (1932, The New York Times), John von Neumann (courtesy of Marina von Neumann Whitman), Oswald Veblen (early 1930s, from the Archives of the Institute for Advanced Study).
    [Show full text]
  • List of Members
    LIST OF MEMBERS, ALFRED BAKER, M.A., Professor of Mathematics, University of Toronto, Toronto, Canada. ARTHUR LATHAM BAKER, C.E., Ph.D., Professor of Mathe­ matics, Stevens School, Hpboken., N. J. MARCUS BAKER, U. S. Geological Survey, Washington, D.C. JAMES MARCUS BANDY, B.A., M.A., Professor of Mathe­ matics and Engineering, Trinit)^ College, N. C. EDGAR WALES BASS, Professor of Mathematics, U. S. Mili­ tary Academy, West Point, N. Y. WOOSTER WOODRUFF BEMAN, B.A., M.A., Member of the London Mathematical Society, Professor of Mathe­ matics, University of Michigan, Ann Arbor, Mich. R. DANIEL BOHANNAN, B.Sc, CE., E.M., Professor of Mathematics and Astronomy, Ohio State University, Columbus, Ohio. CHARLES AUGUSTUS BORST, M.A., Assistant in Astronomy, Johns Hopkins University, Baltimore, Md. EDWARD ALBERT BOWSER, CE., LL.D., Professor of Mathe­ matics, Rutgers College, New Brunswick, N. J. JOHN MILTON BROOKS, B.A., Instructor in Mathematics, College of New Jersey, Princeton, N. J. ABRAM ROGERS BULLIS, B.SC, B.C.E., Macedon, Wayne Co., N. Y. WILLIAM ELWOOD BYERLY, Ph.D., Professor of Mathematics, Harvard University, Cambridge*, Mass. WILLIAM CAIN, C.E., Professor of Mathematics and Eng­ ineering, University of North Carolina, Chapel Hill, N. C. CHARLES HENRY CHANDLER, M.A., Professor of Mathe­ matics, Ripon College, Ripon, Wis. ALEXANDER SMYTH CHRISTIE, LL.M., Chief of Tidal Division, U. S. Coast and Geodetic Survey, Washington, D. C. JOHN EMORY CLARK, M.A., Professor of Mathematics, Yale University, New Haven, Conn. FRANK NELSON COLE, Ph.D., Assistant Professor of Mathe­ matics, University of Michigan, Ann Arbor, Mich.
    [Show full text]
  • Academic Genealogy of the Oakland University Department Of
    Basilios Bessarion Mystras 1436 Guarino da Verona Johannes Argyropoulos 1408 Università di Padova 1444 Academic Genealogy of the Oakland University Vittorino da Feltre Marsilio Ficino Cristoforo Landino Università di Padova 1416 Università di Firenze 1462 Theodoros Gazes Ognibene (Omnibonus Leonicenus) Bonisoli da Lonigo Angelo Poliziano Florens Florentius Radwyn Radewyns Geert Gerardus Magnus Groote Università di Mantova 1433 Università di Mantova Università di Firenze 1477 Constantinople 1433 DepartmentThe Mathematics Genealogy Project of is a serviceMathematics of North Dakota State University and and the American Statistics Mathematical Society. Demetrios Chalcocondyles http://www.mathgenealogy.org/ Heinrich von Langenstein Gaetano da Thiene Sigismondo Polcastro Leo Outers Moses Perez Scipione Fortiguerra Rudolf Agricola Thomas von Kempen à Kempis Jacob ben Jehiel Loans Accademia Romana 1452 Université de Paris 1363, 1375 Université Catholique de Louvain 1485 Università di Firenze 1493 Università degli Studi di Ferrara 1478 Mystras 1452 Jan Standonck Johann (Johannes Kapnion) Reuchlin Johannes von Gmunden Nicoletto Vernia Pietro Roccabonella Pelope Maarten (Martinus Dorpius) van Dorp Jean Tagault François Dubois Janus Lascaris Girolamo (Hieronymus Aleander) Aleandro Matthaeus Adrianus Alexander Hegius Johannes Stöffler Collège Sainte-Barbe 1474 Universität Basel 1477 Universität Wien 1406 Università di Padova Università di Padova Université Catholique de Louvain 1504, 1515 Université de Paris 1516 Università di Padova 1472 Università
    [Show full text]
  • View Front and Back Matter from The
    TRANSACTIONS OF THE American Mathematical Society EDITED BY ElilAKIM HASTINGS MOOBE EDWARD BURR VAN VLECK HENRY SEELY WHITE WITH THE COOPERATION OF CHARLES LEONARD BOTJTON LEONARD EUGENE DICKSON JOHN IHWIN HUTCHINSON EDWARD KASNEH EDWIN BLDWELL WILSON J'UBLIWHEll QCABTEILT BI THE tSOCIKTT WITH THB BUPPOBT OF Yale University Nobthwestekn University Columbia University The University of Illinois Wesleyan University Cornell University ilavehfobd college the university of chicago The University of Missouri Stanford University Volume 8 1907 Lancaster, Pa., and New Yobk THE MACMIIXAN COMPANY Agents fob the Society 1907 Reprinted with the permission of The American Mathematical Society Johnson Reprint Corporation 111 Fifth Avenue, New York 3, N. Y. Johnson Reprint Company Limited Berkeley Square House, London, W. 1 First Reprinting, 1963, Johnson Reprint Corporation TABLE OF CONTENTS VOLUME 8 1907 PAGES Blichfeldt, H. F., of Stanford University, Cal. On modular groups isomorphic with a given linear group.30- 32 Bliss, Gilbert Ames, of Princeton, N. J. A new form of the simplest problem of the calculus of variations.405—414 Bolza, Oskar, of Chicago, 111. Existence proof for a field of extremals tangent to a given curve.399-404 Dickson, Leonard Eugene, of Chicago, 111. Invariants of binary forms under modular transformations.205-232 _Modular theory of group-matrices.389—398 Eisenhart, Luther Pfahler, of Princeton, N. J. Applicable surfaces with asymptotic lines of one surface corresponding to a conjugate system of another.113—134 Fite, William Benjamin, of Ithaca, N. Y. Irreducible linear homogeneous groups whose orders are powers of a prime . 107—112 Fréchet, Maurice, of Paris, France.
    [Show full text]
  • Rudi Mathematici
    Rudi Mathematici Y2K Rudi Mathematici Gennaio 2000 52 1 S (1803) Guglielmo LIBRI Carucci dalla Somaja Olimpiadi Matematiche (1878) Agner Krarup ERLANG (1894) Satyendranath BOSE P1 (1912) Boris GNEDENKO 2 D (1822) Rudolf Julius Emmanuel CLAUSIUS Due matematici "A" e "B" si sono inventati una (1905) Lev Genrichovich SHNIRELMAN versione particolarmente complessa del "testa o (1938) Anatoly SAMOILENKO croce": viene scritta alla lavagna una matrice 1 3 L (1917) Yuri Alexeievich MITROPOLSHY quadrata con elementi interi casuali; il gioco (1643) Isaac NEWTON consiste poi nel calcolare il determinante: 4 M (1838) Marie Ennemond Camille JORDAN 5 M Se il determinante e` pari, vince "A". (1871) Federigo ENRIQUES (1871) Gino FANO Se il determinante e` dispari, vince "B". (1807) Jozeph Mitza PETZVAL 6 G (1841) Rudolf STURM La probabilita` che un numero sia pari e` 0.5, (1871) Felix Edouard Justin Emile BOREL 7 V ma... Quali sono le probabilita` di vittoria di "A"? (1907) Raymond Edward Alan Christopher PALEY (1888) Richard COURANT P2 8 S (1924) Paul Moritz COHN (1942) Stephen William HAWKING Dimostrare che qualsiasi numero primo (con (1864) Vladimir Adreievich STELKOV l'eccezione di 2 e 5) ha un'infinita` di multipli 9 D nella forma 11....1 2 10 L (1875) Issai SCHUR (1905) Ruth MOUFANG "Die Energie der Welt ist konstant. Die Entroopie 11 M (1545) Guidobaldo DEL MONTE der Welt strebt einem Maximum zu" (1707) Vincenzo RICCATI (1734) Achille Pierre Dionis DU SEJOUR Rudolph CLAUSIUS 12 M (1906) Kurt August HIRSCH " I know not what I appear to the world,
    [Show full text]
  • RM Calendar 2017
    Rudi Mathematici x3 – 6’135x2 + 12’545’291 x – 8’550’637’845 = 0 www.rudimathematici.com 1 S (1803) Guglielmo Libri Carucci dalla Sommaja RM132 (1878) Agner Krarup Erlang Rudi Mathematici (1894) Satyendranath Bose RM168 (1912) Boris Gnedenko 1 2 M (1822) Rudolf Julius Emmanuel Clausius (1905) Lev Genrichovich Shnirelman (1938) Anatoly Samoilenko 3 T (1917) Yuri Alexeievich Mitropolsky January 4 W (1643) Isaac Newton RM071 5 T (1723) Nicole-Reine Etable de Labrière Lepaute (1838) Marie Ennemond Camille Jordan Putnam 2002, A1 (1871) Federigo Enriques RM084 Let k be a fixed positive integer. The n-th derivative of (1871) Gino Fano k k n+1 1/( x −1) has the form P n(x)/(x −1) where P n(x) is a 6 F (1807) Jozeph Mitza Petzval polynomial. Find P n(1). (1841) Rudolf Sturm 7 S (1871) Felix Edouard Justin Emile Borel A college football coach walked into the locker room (1907) Raymond Edward Alan Christopher Paley before a big game, looked at his star quarterback, and 8 S (1888) Richard Courant RM156 said, “You’re academically ineligible because you failed (1924) Paul Moritz Cohn your math mid-term. But we really need you today. I (1942) Stephen William Hawking talked to your math professor, and he said that if you 2 9 M (1864) Vladimir Adreievich Steklov can answer just one question correctly, then you can (1915) Mollie Orshansky play today. So, pay attention. I really need you to 10 T (1875) Issai Schur concentrate on the question I’m about to ask you.” (1905) Ruth Moufang “Okay, coach,” the player agreed.
    [Show full text]
  • Hilbert in Missouri Author(S): David Zitarelli Reviewed Work(S): Source: Mathematics Magazine, Vol
    Hilbert in Missouri Author(s): David Zitarelli Reviewed work(s): Source: Mathematics Magazine, Vol. 84, No. 5 (December 2011), pp. 351-364 Published by: Mathematical Association of America Stable URL: http://www.jstor.org/stable/10.4169/math.mag.84.5.351 . Accessed: 22/01/2012 11:15 Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at . http://www.jstor.org/page/info/about/policies/terms.jsp JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. Mathematical Association of America is collaborating with JSTOR to digitize, preserve and extend access to Mathematics Magazine. http://www.jstor.org VOL. 84, NO. 5, DECEMBER 2011 351 Hilbert in Missouri DAVIDZITARELLI Temple University Philadelphia, PA 19122 [email protected] No, David Hilbert never visited Missouri. In fact, he never crossed the Atlantic. Yet doctoral students he produced at Gottingen¨ played important roles in the development of mathematics during the first quarter of the twentieth century in what was then the southwestern part of the United States, particularly in that state. It is well known that Felix Klein exerted a primary influence on the emerging American mathematical research community at the end of the nineteenth century by mentoring students and educating professors in Germany as well as lecturing in the U.S.
    [Show full text]
  • U Iversidad Del Valle De Guatemala
    UIVERSIDAD DEL VALLE DE GUATEMALA Facultad de Ciencias y Humanidades Análisis de Cantor-Bendixson: La Hipótesis del Continuo para espacios polacos Gabriel Enrique Girón Garnica Guatemala 2008 Análisis de Cantor-Bendixson: La Hipótesis del Continuo para espacios polacos UIVERSIDAD DEL VALLE DE GUATEMALA Facultad de Ciencias y Humanidades Análisis de Cantor-Bendixson: La Hipótesis del Continuo para espacios polacos Trabajo de graduación presentado por Gabriel Enrique Girón Garnica para optar al grado académico de Licenciado en Matemática Guatemala 2008 Vo. Bo.: (f)_____________________________ PhD. L. Pedro Poitevin Asesor Tribunal: (f)_____________________________ Lic. Dorval Carías (f)_____________________________ PhD. L. Pedro Poitevin (f)_____________________________ Licda. María Eugenia de Nieves Fecha de aprobación: 19 de diciembre de 2008. «Creo que la verdad está bien en la matemática…. o en la vida. En la vida es más importante la ilusión, la imaginación, el deseo, la esperanza. Además, ¿sabemos acaso lo que es la verdad? Si yo le digo que aquel trozo de ventana es azul, digo una verdad. Pero es una verdad parcial, y por lo tanto una especie de mentira. Porque ese trozo de ventana no está solo, está en una casa, en una ciudad, en un paisaje. Está rodeado del gris de ese muro de cemento, del azul claro de este cielo, de aquellas nubes alargadas, de infinitas cosas más. Y si no digo todo, absolutamente todo, estoy mintiendo. Pero decir todo es imposible, aun en este caso de la ventana, de un simple trozo de la realidad física, de la simple realidad física. La realidad es infinita y además infinitamente matizada, y si me olvido de un solo matiz ya estoy mintiendo.
    [Show full text]
  • The First One Hundred Years
    The Maryland‐District of Columbia‐Virginia Section of the Mathematical Association of America: The First One Hundred Years Caren Diefenderfer Betty Mayfield Jon Scott November 2016 v. 1.3 The Beginnings Jon Scott, Montgomery College The Maryland‐District of Columbia‐Virginia Section of the Mathematical Association of America (MAA) was established, just one year after the MAA itself, on December 29, 1916 at the Second Annual Meeting of the Association held at Columbia University in New York City. In the minutes of the Council Meeting, we find the following: A section of the Association was established for Maryland and the District of Columbia, with the possible inclusion of Virginia. Professor Abraham Cohen, of Johns Hopkins University, is the secretary. We also find, in “Notes on the Annual Meeting of the Association” published in the February, 1917 Monthly, The Maryland Section has just been organized and was admitted by the council at the New York meeting. Hearty cooperation and much enthusiasm were reported in connection with this section. The phrase “with the possible inclusion of Virginia” is curious, as members from all three jurisdictions were present at the New York meeting: seven from Maryland, one from DC, and three from Virginia. However, the report, “Organization of the Maryland‐Virginia‐District of Columbia Section of the Association” (note the order!) begins As a result of preliminary correspondence, a group of Maryland mathematicians held a meeting in New York at the time of the December meeting of the Association and presented a petition to the Council for authority to organize a section of the Association in Maryland, Virginia, and the District of Columbia.
    [Show full text]
  • An Outline of the History of Mathematics in the U
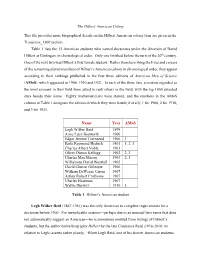
    The Hilbert American Colony This file provides more biographical details on the Hilbert American colony than are given in the Transition_1900 section. Table 1 lists the 13 American students who earned doctorates under the direction of David Hilbert at Göttingen, in chronological order. Only one finished before the turn of the 20th century. One of the next two was Hilbert’s first female student. Rather than describing the lives and careers of the remaining eleven members of Hilbert’s American colony in chronological order, they appear according to their rankings published in the first three editions of American Men of Science (AMoS), which appeared in 1906, 1910 and 1921. In each of the three lists, scientists regarded as the most eminent in their field were asked to rank others in the field, with the top 1000 awarded stars beside their name. Eighty mathematicians were starred, and the numbers in the AMoS column in Table 1 designate the edition in which they were listed (if at all): 1 for 1906, 2 for 1910, and 3 for 1921. Name Year AMoS Legh Wilber Reid 1899 Anne Lucy Bosworth 1900 Edgar Jerome Townsend 1900 3 Earle Raymond Hedrick 1901 1, 2, 3 Charles Albert Noble 1901 Oliver Dimon Kellogg 1902 2, 3 Charles Max Mason 1903 2, 3 Wilhelmus David Westfall 1905 David Clinton Gillespie 1906 William DeWeese Cairns 1907 Arthur Robert Crathorne 1907 Charles Haseman 1907 Wallie Hurwitz 1910 3 Table 1: Hilbert’s American student Legh Wilber Reid (1867-1961) was the only American to complete requirements for a doctorate before 1900.
    [Show full text]
  • From Robson Technique to Morley's Trisector Theorem
    FROM ROBSON TECHNIQUE TO MORLEY's TRISECTOR THEOREM Jean - Louis AYME A 3 2' L Q 2 N R 3' M P B C 1 1' Abstract. The author presents the forgotten synthetic proof of Alan Robson concerning the Morley's trisector theorem. Short biographies, the digital journal Revistaoim and two archives are given. The figures are all in general position and all the theorems quoted can be proved synthetically. 2 Summary A. Robson technique 2 1. Two isogonal lines from Darij Grinberg 2. Hesse theorem 's 3. A short biography of Ludwig Otto Hesse 4. Robson technique to prove that three diagonals are concurrent 5. About Revistaoim 6. A very short biography of Alan Robson B. Two nice applications 11 I. Morley 's trisector theorem 11 1. The problem 2. A short biography of Frank Morley II. Jacobi 's theorem 18 1. The problem 2. Comment C. Appendix 19 I. Anharmonic ratio of four collinear points 19 1. Definition 2. Two remarkable results II. Anharmonic ratio of four concurrent lines 1. Definition D. Annex 21 1. Angle I E. Archives 22 A. ROBSON TECHNIQUE 1. Two isogonal lines from Darij Grinberg VISION Figure : A 1 1' X P Q Y B C Features : ABC a triangle, 1, 1' two A-isogonal lines of ABC, 2 3 P, Q two points resp. on 1, 1' and X, Y the points of intersection resp. of BP and CQ, BQ and CP. Given : AX and AY are two A-isogonal lines of ABC. 1 VISUALIZATION A 1' U 1 Q' M X V P Q Y' B C • Note Q', U, V the points of intersection resp.
    [Show full text]
  • RM Calendar 2011
    Rudi Mathematici x4-8.212x3+25.286.894x2-34.603.963.748x+17.756.354.226.585 =0 Rudi Mathematici January 1 S (1894) Satyendranath BOSE Putnam 1996 - A1 (1878) Agner Krarup ERLANG (1912) Boris GNEDENKO Find the least number A such that for any two (1803) Guglielmo LIBRI Carucci dalla Sommaja RM132 squares of combined area 1, a rectangle of 2 S (1822) Rudolf Julius Emmanuel CLAUSIUS area A exists such that the two squares can be (1938) Anatoly SAMOILENKO packed in the rectangle (without interior (1905) Lev Genrichovich SHNIRELMAN overlap). You may assume that the sides of 1 3 M (1917) Yuri Alexeievich MITROPOLSKY the squares are parallel to the sides of the rectangle. 4 T (1643) Isaac NEWTON RM071 5 W (1871) Federigo ENRIQUES RM084 Math pickup lines (1871) Gino FANO (1838) Marie Ennemond Camille JORDAN My love for you is a monotonically increasing 6 T (1807) Jozeph Mitza PETZVAL unbounded function. (1841) Rudolf STURM MathJokes4MathyFolks 7 F (1871) Felix Edouard Justin Emile BOREL (1907) Raymond Edward Alan Christopher PALEY Ten percent of all car thieves are left-handed. 8 S (1924) Paul Moritz COHN All polar bears are left-handed. (1888) Richard COURANT If your car is stolen, there’s a 10% chance it (1942) Stephen William HAWKING was taken by a polar bear. 9 S (1864) Vladimir Adreievich STEKLOV The description of right lines and circles, upon 2 10 M (1905) Ruth MOUFANG which geometry is founded, belongs to (1875) Issai SCHUR mechanics. Geometry does not teach us to 11 T (1545) Guidobaldo DEL MONTE RM120 draw these lines, but requires them to be (1734) Achille Pierre Dionis DU SEJOUR drawn.
    [Show full text]