DOCSLIB.ORG

Characterization of Fracture Initiation in Non-Cylindrical Buckle Folds Using 3D Finite Element Analysis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Characterization of Fracture Initiation in Non-Cylindrical Buckle Folds Using 3D Finite Element Analysis Scholars' Mine Masters Theses Student Theses and Dissertations Summer 2016 Characterization of fracture initiation in non-cylindrical buckle folds using 3D finite element analysis Eli Jacob Steinbeck Follow this and additional works at: https://scholarsmine.mst.edu/masters_theses Part of the Geology Commons, and the Petroleum Engineering Commons Department: Recommended Citation Steinbeck, Eli Jacob, "Characterization of fracture initiation in non-cylindrical buckle folds using 3D finite element analysis" (2016). Masters Theses. 7570. https://scholarsmine.mst.edu/masters_theses/7570 This thesis is brought to you by Scholars' Mine, a service of the Missouri S&T Library and Learning Resources. This work is protected by U. S. Copyright Law. Unauthorized use including reproduction for redistribution requires the permission of the copyright holder. For more information, please contact [email protected]. CHARACTERIZATION OF FRACTURE INITIATION IN NON-CYLINDRICAL BUCKLE FOLDS USING 3D FINITE ELEMENT ANALYSIS by ELI JACOB STEINBECK A THESIS Presented to the Faculty of the Graduate School of the MISSOURI UNIVERSITY OF SCIENCE AND TECHNOLOGY In Partial Fulfillment of the Requirements for the Degree MASTER OF SCIENCE IN PETROLEUM ENGINEERING 2016 Approved by Dr. Andreas Eckert, Advisor Dr. John Hogan Dr. Runar Nygaard 2016 Eli Jacob Steinbeck All Rights Reserved iii ABSTRACT The spatial distribution of fracture sets associated with buckle folds has been well documented in field studies. There are difficulties, however, in placing accurate constraints on the timing of the initiation of individual fracture sets during the deformation history of the fold under in-situ conditions. This study investigates specific conditions that give rise to the initiation of various fracture sets in the hinge and limb of a pericline, based on an analysis of the effective stress evolution during the processes of buckling and erosional unloading. A 3D finite element modeling approach is used to simulate the effective stress evolution in single-layer folds with a Maxwell viscoelastic rheology, while including the influence of overburden stress, pore pressure, and a geologic strain rate. Several material properties and geometric features are varied to test their influence on fracture initiation. The modeling results show that fracturing is most heavily influenced by permeability, initial overburden thickness, and erosional unloading. Further analysis reveals that six fracture sets, which are observed in natural buckle folds, are also observed in the modeling results: outer arc tensile fractures, outer arc normal faults, and inner arc thrusts, all of which strike parallel to the fold axis, are determined to be common fracture sets; outer arc tensile fractures that strike perpendicular to the fold axis, and thrusts in the limb that strike roughly parallel to the fold axis are determined to be less common fracture sets that require low permeability (< 10-21 m2) folding layers in order to initiate; vertical conjugate shear fractures in the outer arc, where the fold axis bisects the acute angle between fracture planes, are determined to be a rare fracture set. Most importantly, the timing of initiation is determined for each set, thus providing the most difficult information to obtain from a field study on fold related fractures. iv ACKNOWLEDGMENTS I would like to thank my advisor, Dr. Andreas Eckert, for accepting me into the geomechanical modeling group. During my time as an undergraduate he was very influential in my decision to pursue a master’s degree, and throughout my last two years as a graduate student he has been a supportive and encouraging mentor and friend. His theoretical knowledge and technical guidance have proven to be invaluable tools that have helped guide me through my research and on to the completion of this thesis. I would also like to thank Dr. John Hogan and Dr. Runar Nygaard for the time and effort they have put forth as members of my graduate committee. Your advice regarding this thesis, my current academic career, and my future career in the petroleum industry has been very much appreciated. My thanks also go to my friends and colleagues that are, or have been a part of the geomechanical modeling group: Xiaolong Liu, Weicheng Zhang, Davi Rodrigues Damasceno, Huining Zhang, Zhe Yuan, and Mengke Li. Thank you all for all your help and support during my time as a master’s student; and most importantly, thank you for your friendship, and for keeping me sane during all those hours spent in B21 McNutt. Lastly I would like to thank my family: my parents, my sister Hannah, and my fiancée Erika Miller. Thank you for your unwavering love, and endless support and encouragement in all of my endeavors. You will always be my primary motivator to strive for success in everything that I do. v TABLE OF CONTENTS Page ABSTRACT ....................................................................................................................... iii ACKNOWLEDGMENTS ................................................................................................. iv LIST OF ILLUSTRATIONS ........................................................................................... viii LIST OF TABLES ............................................................................................................. xi NOMENCLATURE ......................................................................................................... xii SECTION 1. INTRODUCTION ...................................................................................................... 1 1.1. OVERVIEW ....................................................................................................... 1 1.2. LITERATURE REVIEW ................................................................................... 5 1.2.1. Non-cylindrical Folding in Three Dimensions ......................................... 5 1.2.2. Periclines .................................................................................................. 8 1.2.3. Fracture Patterns Associated With Buckle Folding ............................... 10 1.2.4. Limitations of Existing Literature .......................................................... 13 1.3. RESEARCH OBJECTIVES AND QUESTIONS ............................................ 14 2. THEORETICAL BACKGROUND ......................................................................... 16 2.1. ROCK PROPERTIES AND ROCK MECHANICS......................................... 16 2.2. BUCKLE FOLDING THEORY ....................................................................... 17 2.2.1. Single Layer Fold Theory ....................................................................... 17 2.2.2. Stress Distribution and Evolution in Buckle Folds ................................ 19 2.2.3. Strain Distribution in Buckle Folds ........................................................ 20 2.3. FRACTURE PREDICTION ............................................................................. 22 2.3.1. Combined Griffith/Navier-Coulomb Failure Criterion .......................... 23 2.3.2. Fracture Potential ................................................................................... 26 2.4. STEREOGRAPHIC PROJECTIONS AND STEREONETS ........................... 28 2.4.1. Plotting Lines on a Stereonet .................................................................. 29 2.4.2. Plotting Planes on a Stereonet ................................................................ 30 2.5. FINITE ELEMENT METHOD ........................................................................ 31 2.5.1. The Standard Discrete System ............................................................... 32 vi 2.5.2. The General Finite Element Method ...................................................... 33 3. METHODOLOGY ................................................................................................... 36 3.1. NUMERICAL MODELING APPROACH ...................................................... 36 3.1.1. Governing Equations for 3D Viscoelastic Folding ................................ 36 3.1.2. The ABAQUSTM Solver ......................................................................... 38 3.2. MODEL SETUP ............................................................................................... 39 3.2.1. Material Properties ................................................................................. 39 3.2.2. Model Geometry ..................................................................................... 42 3.2.3. Loading Procedures ................................................................................ 45 4. RESULTS ................................................................................................................. 48 4.1. BASE MODEL RESULTS ANALYSIS .......................................................... 48 4.1.1. Stress Analysis ....................................................................................... 51 4.1.2. Fracture Potential Results ....................................................................... 55 4.2. PARAMETRIC ANALYSIS ............................................................................ 58 4.2.1. Influence of Permeability Magnitude ..................................................... 58 4.2.2. Influence of Anisotropic Permeability ................................................... 61 4.2.2.1 High permeability buckling ........................................................61 4.2.2.2 Low permeability buckling .........................................................63
Load more

Recommended publications
  • Poster Final
    Evidence for polyphase deformation in the mylonitic zones bounding the Chester and Athens Domes, in southeastern Vermont, from 40Ar/39Ar geochronology Schnalzer, K., Webb, L., McCarthy, K., University of Vermont Department of Geology, Burlington Vermont, USA CLM 40 39 Sample Mineral Assemblage Metamorphic Facies Abstract Microstructure and Ar/ Ar Geochronology 18CD08A Quartz, Muscovite, Biotite, Feldspar, Epidote Upper Greenschist to Lower Amphibolite The Chester and Athens Domes are a composite mantled gneiss QC Twelve samples were collected during the fall of 2018 from the shear zones bounding the Chester and Athens Domes for 18CD08B Quartz, Biotite, Feldspar, Amphibole Amphibolite Facies 18CD08C Quartz, Muscovite, Biotite, Feldspar, Epidote Upper Greenschist to Lower Amphibolite dome in southeast Vermont. While debate persists regarding Me 40 39 microstructural analysis and Ar/ Ar age dating. These samples were divided between two transects, one in the northeastern 18CD08D Quartz, Muscovite, Biotite, Feldspar, Garnet Upper Greenschist to Lower Amphibolite the mechanisms of dome formation, most workers consider the VT NH section of the Chester dome and the second in the southern section of the Athens dome. These samples were analyzed by X-ray 18CD08E Quartz, Muscovite Greenschist Facies domes to have formed during the Acadian Orogeny. This study diraction in the fall of 2018. Oriented, orthogonal thin sections were also prepared for each of the twelve samples. The thin sec- 18CD09A Quartz, Amphibole Amphib olite Facies 40 CVGT integrates the results of Ar/Ar step-heating of single mineral NY tions named with an “X” were cut parallel to the stretching lineation (X) and normal to the foliation (Z) whereas the thin sections 18CD09B Quartz, Biotite, Feldspar, Amphibole, Muscovite Amphibolite Facies grains, or small multigrain aliquots, with data from microstruc- 18CD09C Quartz, Amphibole, Feldspar Amphibolite Facies named with a “Y” have been cut perpendicular to the ‘X-Z’ thin section.
    [Show full text]
  • 326-97 Lab Final S.D
    Geol 326-97 Name: KEY 5/6/97 Class Ave = 101 / 150 Geol 326-97 Lab Final s.d. = 24 This lab final exam is worth 150 points of your total grade. Each lettered question is worth 15 points. Read through it all first to find out what you need to do. List all of your answers on these pages and attach any constructions, tracing paper overlays, etc. Put your name on all pages. 1. One way to analyze brittle faults is to calculate and plot the infinitesimal shortening and extension directions on a lower hemisphere, stereographic projection. These principal axes lie in the “movement plane”, which contains the pole to the fault plane and the slickensides, and are at 45° to the pole. The following questions apply to a single fault described in part (a), below: (a) A fault has a strike and dip of 250, 57 N and the slickensides have a rake of 63°, measured from the given strike azimuth. Plot the orientations of the fault plane and the slickensides on an equal area projection. (b) Bedding in the vicinity of the fault is oriented 37, 42 E. Assuming that the fault formed when the bedding was horizontal, determine and plot the original geometry of the fault and the slickensides. (c) Determine the original (pre-rotation)orientation of the infinitesimal shortening and extension axes for fault. 2. All of the following questions apply to the map shown on the next page. In all of the rocks with cleavage, you may assume that both cleavage and bedding strike 024°.
    [Show full text]
  • Sedimentary Record of Cretaceous And
    SEDIMENT AR Y RECORD OF CRETACEOUS AND TER TIAR Y SALT MOVEMENT, EAST TEXAS BASIN: TIMES, RATES, AND LUMES OF SALT FLOW, IMPLICATIONS TO NUCLEAR-WA TE ISOLATION AND PETROLEUM EXPLO ATION by Steven J. Seni and M. P. A. ackson This work was supported by U.S. Depart ent of Energy and funded under Contract No. DE-AC 7-80ET46617 CONTENTS ABSTRACT . • 00 INTRODUCTION. • 00 Data Base. • 00 Early History of Basin Formation and Infilling • 00 Geometry of Salt Structures • 00 EVOLUTIONARY STAGES OF DOME GROWTH. • 00 Pillow Stage . • 00 Geometry of Overlying Strata . • 00 Geometry of Surrounding Strata • 00 Depositional Facies and Lithostratigraph • 00 Diapir Stage • • 00 Geometry of Surrounding Strata • 00 Depositional Facies and Lithostratigraph • 00 Post-Diapir Stage • 00 Geometry of Surrounding Strata • 00 Depositional Facies and Lithostratigraphy • 00 Holocene Analogues. • 00 Discussion • 00 Significance to Subtle Petroleum Traps • 00 PATTERNS OF SALT MOVEMENT IN TIME AND SPAC • 00 Group 1: Pre-Glen Rose Subgroup (pre-112 Ma) - Periphery of Diapir Province • • 00 Group 2: Glen Rose Subgroup to Washita Group 112 to 98 Ma)-­ Basin Axis • 00 Group 3: Post-Austin Group (86 to 56 Ma) -- Per phery of Diapir Province • • 00 Initiation and Acceleration of Salt Flow • • 00 Overview of Dome History • • 00 RATES OF SALT MOVEMENT AND DOME GROWTH • • 00 Assumptions • • 00 Proven Propositions. • 00 Unproven Propositions • 00 Incorrect Propositions • • 00 Distinguishing Between Syndepositional and Post-D positional Thickness Variations. • 00 The Problem • • 00 Structural Evidence • • 00 Sedimentological Evidence • • 00 Methodology • • 00 Distinguishing Between Regional and Salt-Re ated Thickness Variations. • 00 Volume of Salt Mobilized and Estimates of S t Loss • 00 Rates of Dome Growth • • 00 Net Rates of Pillow Growth • 00 Net Rates of Diapir Growth • 00 Gross Rates of Diapir Growth • • 00 Growth Rates and Strain Rates • 00 IMPLICA TIONS TO WASTE ISOLATION • • 00 CONCLUSIONS • • 00 ACKNOWLEDGMENTS • • 00 REFERENCES • 00 APPENDICES • 00 Figures 1.
    [Show full text]
  • Influences of Surface Processes on Fold Growth During 3D Detachment
    PUBLICATIONS Geochemistry, Geophysics, Geosystems RESEARCH ARTICLE Influences of surface processes on fold growth during 3-D 10.1002/2014GC005450 detachment folding Key Point: M. Collignon1, B. J. P. Kaus2, D. A. May3, and N. Fernandez2 Influences of surface processes on the fold pattern in fold-and-thrust 1Geological Institute, ETH Zurich, Zurich, Switzerland, 2Institut fur€ Geowissenschaften, Johannes Gutenberg-Universit€at, belts Mainz, Germany, 3Institute of Geophysics, ETH Zurich, Zurich, Switzerland Correspondence to: M. Collignon, Abstract In order to understand the interactions between surface processes and multilayer folding sys- [email protected] tems, we here present fully coupled three-dimensional numerical simulations. The mechanical model repre- sents a sedimentary cover with internal weak layers, detached over a much weaker basal layer representing Citation: salt or evaporites. Applying compression in one direction results in a series of three-dimensional buckle folds, Collignon, M., B. J. P. Kaus, D. A. May, and N. Fernandez (2014), Influences of of which the topographic expression consists of anticlines and synclines. This topography is modified through surface processes on fold growth time by mass redistribution, which is achieved by a combination of fluvial and hillslope erosion, as well as during 3-D detachment folding, deposition, and which can in return influence the subsequent deformation. Model results show that surface Geochem. Geophys. Geosyst., 15, doi:10.1002/2014GC005450. processes do not have a significant influence on folding patterns and aspect ratio of the folds. Nevertheless, erosion reduces the amount of shortening required to initiate folding and increases the exhumation rates. Received 9 JUN 2014 Increased sedimentation in the synclines contributes to this effect by amplifying the fold growth rate by grav- Accepted 29 JUL 2014 ity.
    [Show full text]
  • Pacific Petroleum Eology
    Pacific Petroleum Geology NEWSLETTER Pacific Section • American Association of Petroleum Geologists September & October• 2010 School of Rock Ridge Basin CONTENTS 2010-2011 OFF I C E RS EV E RY ISSU E President Cynthia Huggins 661.665.5074 [email protected] 4 Message from the President • C. Huggins President-Elect John Minch 805.898.9200 6 Editor’s Corner • E. Washburn [email protected] Vice President Jeff Gartland 7 PS-AAPG News 661.869.8204 [email protected] 13 Publications Secretary Tony Reid 661.412.5467 17 Member Society News [email protected] Treasurer 2009-2011 Cheryl Blume TH I S ISSU E 661.864.4722 [email protected] 8 Sharktooth Hill Fossil Fund • K. Hancharick Treasurer 2010-2012 Jana McIntyre 661.869.8231 [email protected] 10 AAPG Young Professionals • J. Allen Past President Scott Hector 11 Serpentine: The Rest of the Story • Mel 707.974.6402 [email protected] Erskine Editor-in-Chief Ed Washburn 661.654.7182 [email protected] ST AFF Web Master Bob Countryman 661.589.8580 [email protected] Membership Chair Brian Church 661.654.7863 [email protected] Publications Chair Larry Knauer 661.392.2471 [email protected] [email protected] Advisory Council Representative Kurt Neher 661.412.5203 [email protected] Cover photo of Ridge Basin outcrop courtesy Jonathan Allen Page 3 Pacific Petroleum Geologist Newsletter September & October • 2010 MESSAGE FRO M THE PRESIDENT CYNTHIA HUGGINS Do you know what Marilyn Bachman, Mike Fillipow, Peggy Lubchenco, and Jane Justus Frazier have in common? They were all recipients of the Teacher of the Year Award from AAPG, and they all came from the Pacific Section! Of the 13 recipients of this award, four have been from PSAAPG.
    [Show full text]
  • Chapter 01.Pdf
    Mathematical Background in Aircraft Structural Mechanics CHAPTER 1. Linear Elasticity SangJoon Shin School of Mechanical and Aerospace Engineering Seoul National University Active Aeroelasticityand Rotorcraft Lab. Basic equation of Linear Elasticity Structural analysis … evaluation of deformations and stresses arising within a solid object under the action of applied loads - if time is not explicitly considered as an independent variable → the analysis is said to be static → otherwise, structural dynamic analysis or structural dynamics Small deformation Under the assumption of { Linearly elastic material behavior - Three dimensional formulation → a set of 15 linear 1st order PDE involving displacement field (3 components) { stress field (6 components) strain field (6 components) plane stress problem → simpler, 2-D formulations { plane strain problem For most situations, not possible to develop analytical solutions → analysis of structural components … bars, beams, plates, shells 1-2 Active Aeroelasticity and Rotorcraft Lab., Seoul National University 1.1 The concept of Stress 1.1.1 The state of stress at a point State of stress in a solid body… measure of intensity of forces acting within the solid - distribution of forces and moments appearing on the surface of the cut … equipollent force F , and couple M - Newton’s 3rd law → a force and couple of equal magnitudes and opposite directions acting on the two forces created by the cut Fig. 1.1 A solid body cut by a plane to isolate a free body 1-3 Active Aeroelasticity and Rotorcraft
    [Show full text]
  • Folds and Folding
    Chapter ................................ 11 Folds and folding Folds are eye-catching and visually attractive structures that can form in practically any rock type, tectonic setting and depth. For these reasons they have been recognized, admired and explored since long before geology became a science (Leonardo da Vinci discussed them some 500 years ago, and Nicholas Steno in 1669). Our understanding of folds and folding has changed over time, and the fundament of what is today called modern fold theory was more or less consolidated in the 1950s and 1960s. Folds, whether observed on the micro-, meso- or macroscale, are clearly some of our most important windows into local and regional deformation histories of the past. Their geometry and expression carry important information about the type of deformation, kinematics and tectonics of an area. Besides, they can be of great economic importance, both as oil traps and in the search for and exploitation of ores and other mineral resources. In this chapter we will first look at the geometric aspects of folds and then pay attention to the processes and mechanisms at work during folding of rock layers. 220 Folds and folding 11.1 Geometric description (a) Kink band a a It is fascinating to watch folds form and develop in the laboratory, and we can learn much about folds and folding by performing controlled physical experiments and numerical simulations. However, modeling must always be rooted in observations of naturally folded Trace of Axial trace rocks, so geometric analysis of folds formed in different bisecting surface settings and rock types is fundamental. Geometric analy- (b) Chevron folds sis is important not only in order to understand how various types of folds form, but also when considering such things as hydrocarbon traps and folded ores in the subsurface.
    [Show full text]
  • The Role of Flexural Slip in the Development of Chevron Folds
    Scholars' Mine Masters Theses Student Theses and Dissertations Spring 2018 The role of flexural slip in the development of chevron folds Yuxing Wu Follow this and additional works at: https://scholarsmine.mst.edu/masters_theses Part of the Petroleum Engineering Commons Department: Recommended Citation Wu, Yuxing, "The role of flexural slip in the development of chevron folds" (2018). Masters Theses. 7788. https://scholarsmine.mst.edu/masters_theses/7788 This thesis is brought to you by Scholars' Mine, a service of the Missouri S&T Library and Learning Resources. This work is protected by U. S. Copyright Law. Unauthorized use including reproduction for redistribution requires the permission of the copyright holder. For more information, please contact [email protected]. i THE ROLE OF FLEXURAL SLIP IN THE DEVELOPMENT OF CHEVRON FOLDS by YUXING WU A THESIS Presented to the Faculty of the Graduate School of the MISSOURI UNIVERSITY OF SCIENCE AND TECHNOLOGY In Partial Fulfillment of the Requirements for the Degree MASTER OF SCIENCE IN PETROLEUM ENGINEERING 2018 Approved by Andreas Eckert, Advisor John Patrick Hogan Jonathan Obrist Farner ii 2018 Yuxing Wu All Rights Reserved iii ABSTRACT Chevron folds are characterized by straight limbs and narrow hinge zones. One of the conceptual models to initiate and develop chevron folds involves flexural slip during folding. While some kinematical models show the necessity for slip to initiate during chevron folding, recent numerical modeling studies of visco-elastic effective single layer buckle folding have shown that flexural slip does not result in chevron folds. In this study, several 2D finite element analysis models are run, distinguished by 1) geometry of the initial perturbation (sinusoidal and white noise), 2) varying thewavelength of the initial perturbation (10%, 50%, and 100% of the dominant wavelength) and 3) variation of the friction coefficient (high and low friction coefficient between interlayers).
    [Show full text]
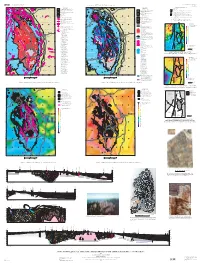
  • Map Showing Geology, Structure, and Geophysics of the Central Black
    U.S. DEPARTMENT OF THE INTERIOR Prepared in cooperation with the SCIENTIFIC INVESTIGATIONS MAP 2777 U.S. GEOLOGICAL SURVEY SOUTH DAKOTA SCHOOL OF MINES AND TECHNOLOGY FOUNDATION SHEET 2 OF 2 Pamphlet accompanies map 104°00' 103°30' 103°00' 104°00' 103°30' 103°00' ° ° EXPLANATION FOR MAPS F TO H 44 30' 44°30' EXPLANATION 44 30' 44°30' EXPLANATION Spearfish Geologic features 53 54 Tertiary igneous rocks (Tertiary and post-Tertiary Spearfish PHANEROZOIC ROCKS 90 1 90 sedimentary rocks not shown) Pringle fault 59 Tertiary igneous rocks (Tertiary and post-Tertiary Pre-Tertiary and Cretaceous (post-Inyan Kara sedimentary rocks not shown) Monocline—BHM, Black Hills monocline; FPM, Fanny Peak monocline 52 85 Group) rocks 85 Sturgis Sturgis Pre-Tertiary and Cretaceous (post-Inyan Kara A Proposed western limit of Early Proterozoic rocks in subsurface 55 Lower Cretaceous (Inyan Kara Group), Jurassic, Group) rocks 57 58 60 14 and Triassic rocks 14 Lower Cretaceous (Inyan Kara Group), Jurassic, B Northern extension (fault?) of Fanny Peak monocline and Triassic rocks Paleozoic rocks C Possible eastern limit of Early Proterozoic rocks in subsurface 50 Paleozoic rocks Precambrian rocks S Possible suture in subsurface separating different tectonic terranes 89 51 89 2 PRECAMBRIAN ROCKS of Sims (1995) 49 Contact St 3 G Harney Peak Granite (unit Xh) Geographic features—BL, Bear Lodge Mountains; BM, Bear Mountain; Fault—Dashed where approximately located G DT DT, Devils Tower 48 B Early Proterozoic rocks, undivided Anticline—Showing trace of axial surface and 1 St Towns and cities—B, Belle Fourche; C, Custer; E, Edgemont; HS, Hot direction of plunge.
    [Show full text]
  • Joints, Folds, and Faults
    Structural Geology Rocks in the Crust Are Bent, Stretched, and Broken … …by directed stresses that cause Deformation. Types of Differential Stress Tensional, Compressive, and Shear Strain is the change in shape and or volume of a rock caused by Stress. Joints, Folds, and Faults Strain occurs in 3 stages: elastic deformation, ductile deformation, brittle deformation 1 Type of Strain Dependent on … • Temperature • Confining Pressure • Rate of Strain • Presence of Water • Composition of the Rock Dip-Slip and Strike-Slip Faults Are the Most Common Types of Faults. Major Fault Types 2 Fault Block Horst and Graben BASIN AND Crustal Extension Formed the RANGE PROVINCE Basin and Range Province. • Decompression melting and high heat developed above a subducted rift zone. • Former margin of Farallon and Pacific plates. • Thickening, uplift ,and tensional stress caused normal faults. • Horst and Graben structures developed. Fold Terminology 3 Open Anticline – convex upward arch with older rocks in the center of the fold (symmetrical) Isoclinal Asymmetrical Overturned Recumbent Evolution Simple Folds of a fold into a reverse fault An eroded anticline will have older beds in the middle An eroded syncline will have younger beds in middle Outcrop patterns 4 • The Strike of a body of rock is a line representing the intersection of A layer of tilted that feature with the plane of the horizon (always measured perpendicular to the Dip). rock can be • Dip is the angle below the horizontal of a geologic feature. represented with a plane. o 30 The orientation of that plane in space is defined with Strike-and- Dip notation. Maps are two- Geologic Map Showing Topography, Lithology, and dimensional Age of Rock Units in “Map View”.
    [Show full text]
  • TIES, MONTANA. by CF BOWEN. Previo
    ANTICLINES IN A PART OF THE MUSSELSHELL VALLEY, MUSSELSHELL, MEAGHER, AND SWEETGRASS COUN­ TIES, MONTANA. By C. F. BOWEN. INTRODUCTION. Previous investigations had shown that the Musselshell Valley, Mont, is an area in which the rocks have undergone considerable folding. On the basis of this information work was begun in June, 1916, to determine the nature and extent of the folds and to make examination as to the possible occurrence of accumulations of oil and gas in them. The work has demonstrated the existence within the area studied of several well-developed anticlines and domes, which seem to offer structurally favorable places for the accumulation of oil and gas. The demonstration of the presence or absence of commercial accumulations of these fluids in the folds has been less conclusive, owing largely to the undeveloped condition of the area. No direct surface indications of oil were observed, but hydrogen sulphide gas escapes from several water seeps in one part of the area. It is also reported that gas was encountered in several wells dug for water. None of these reports could be verified. At the time of the examination drilling operations within the area were confined to two wells. One of these wells, on the Big Elk dome, had reached the Kootenai formation; the other, in the Woman's Pocket anticline, was probably somewhat more than halfway through the Colorado shale. In neither place had oil been discovered. Two other wells, one about 15 miles east of the area and the other about 12 miles south of the central portion of it, had previously been drilled through the Colo­ rado shale without any discovery of oil.
    [Show full text]
  • Deformation in the Hinge Region of a Chevron Fold, Valley and Ridge Province, Central Pennsylvania
    JournalofStructuraIGeolog3`ko{ ~,.No 2, pp 157tolt, h, 1986 (~IUI-~',I41/gc~$03(10~0(Ki Printed in Oreal Britain ~{: ]t~s¢~Pcrgam-n Press lJd Deformation in the hinge region of a chevron fold, Valley and Ridge Province, central Pennsylvania DAVID K. NARAHARA* and DAVID V. WILTSCHKO% Department of Geological Sciences, The University of Michigan, Ann Arbor, Michigan 481(19, U.S A (Received 27 November 1984: accepted in revised form 18 July 1985) Abstract--The hinge region of an asymmetrical chevron fold in sandstone, taken from the Tuscarora Formation of central Pennsylvania. U.S.A., was studied in detail in an attempt to account for the strain that produced the fold shape. The'fold hinge consists of a medium-grained quartz arenite and was deformed predominantly by brittle fracturing and minor amounts of pressure solution and intracrystalline strain. These fractures include: (1) faults, either minor offsets or major limb thrusts, (2) solitary well-healed quartz veins and (3) fibrous quartz veins which are the result of repeated fracturing and healing of grains. The fractures formed during folding as they are observed to cross-cut the authigenic cement. Deformation lamellae and in a few cases, pressure solution, occurred contemporaneously with folding. The fibrous veins appear to have formed as a result of stretching of one limb: the', cross-cut all other structures. Based upon the spatial relationships between the deformation features, we believe that a neutral surface was present during folding, separating zones of compression and extension along the inner and outer arcs, respectively. Using the strain data from the major faults, the fold can be restored back to an interlimb angle of 157°; however, the extension required for such an angle along the outer arc is much more than was actually measured.
    [Show full text]