DOCSLIB.ORG

S9708 - STRONG SCALING HPC APPLICATIONS: BEST PRACTICES with a LATTICE QCD CASE STUDY Kate Clark, Mathias Wagner Lattice Quantum Chromodynamics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
S9708 - STRONG SCALING HPC APPLICATIONS: BEST PRACTICES with a LATTICE QCD CASE STUDY Kate Clark, Mathias Wagner Lattice Quantum Chromodynamics S9708 - STRONG SCALING HPC APPLICATIONS: BEST PRACTICES WITH A LATTICE QCD CASE STUDY Kate Clark, Mathias Wagner Lattice Quantum Chromodynamics QUDA Bandwidth Optimization AGENDA Latency Optimization Multi-node scaling NVSHMEM Summary 2 3",6@0*,/7*A#"./0 QUANTUM CHROMODYNAMICS ! V*0$0$6./A*<.6-2$(,$"#0$"A$-*0$'&,()$A"1)0,$"A$#&-O10$+&?"#R$ F(-*$R1&/(-2<$0?0)-1"K&R#0-(,K<$&#@$-*0$F0&H$A"1)03P ! 6-h,$F*&-$'(#@,$-"R0-*01$-*0$B",6@0$&#@$A#"./0$(#$-*0$E1"-"#$ The strong force is one of the basic+&#@$-*0$#0O-1"#<$&,$F0??$&,$*O#@10@,$"A$"-*01$E&1-()?0,$,00#$(#$ forces of nature (along with gravity, em and weak) &))0?01&-"1$0cE01(K0#-,3P It’s what binds together the quarks and gluons in the proton and the neutron (as well as hundreds of other particles seen in accelerator experiments) Responsible for the particle zoo seen at sub-nuclear scales (mass, decay rate, etc.) QCD is the theory of the strong force It’s a beautiful theory… 1 d4xL(U) ⌦ = [dU]e− ⌦(U) …but h i Z R V*"K&,$M0AA01,"#$C&-("#&?$7))0?01&-"1$i&)(?(-2Z i01K($C&-("#&?$7))0?01&-"1$G&'"1&-"12!3 !"#$%&'()*$+%",-"#$.#(/01,(-23$$4$$5678$95:;;$$4$$8&1)*$;<$=>;; X LATTICE QUANTUM CHROMODYNAMICS Theory is highly non-linear ⇒ cannot solve directly Must resort to numerical methods to make predictions Lattice QCD Discretize spacetime ⇒ 4-d dimensional lattice of size Lx x Ly x Lz x Lt Finite spacetime ⇒ periodic boundary conditions PDEs ⇒ finite difference equations Consumer of 10-20% of public supercomputer cycles Traditionally highly optimized on every HPC platform for the past 30 years Andre Walker-Loud S91010: Accelerating our Understanding of Nuclear Physics and the Early Universe Jiqun Tu S9330: Lattice QCD with Tensor Cores !4 STEPS IN AN LQCD CALCULATION ↵ β ↵ Dij (x, y; U) j (y)=⌘i (x) 1. Generate an ensemble of gluon field configurations “gauge generation” or Ax = b Produced in sequence, with hundreds needed per ensemble Strong scaling required with 100-1000 TFLOPS sustained for several months Simulation Cost ~ a-6 V5/4 50-90% of the runtime is in the linear solver O(1) solve per linear system Target 164 per GPU 2. “Analyze” the configurations Can be farmed out, assuming ~10 TFLOPS per job Task parallelism means that clusters reign supreme here 80-99% of the runtime is in the linear solver Many solves per system, e.g., O(106) Target 244-324 per GPU !5 LATTICE QCD IN A NUTSHELL Multi GPU Parallelization face 1 4 exchange d xL(U) wrap ⌦ = [dU]e− ⌦(U) around h i Z Z R face exchange wrap around experiment) theory' ! ! Tuesday, July 12, 2011 !6 Large&Hadron&Collider& Davies'et#al# Brookhaven*Na,onal*Laboratory* NVIDIA POWERS WORLD'S FASTEST SUPERCOMPUTER Summit Becomes First System To Scale The 100 Petaflops Milestone 122 PF 3 EF 27,648 HPC AI Volta Tensor Core GPUs 7 STRONG SCALING Multiple meanings Same problem size, more nodes, more GPUs Same problem, next generation GPUs Multigrid - strong scaling within the same run (not discussed here) To tame strong scaling we have to understand the limiters Bandwidth limiters Latency limiters !8 QUDA 9 QUDA • “QCD on CUDA” – http://lattice.github.com/quda (open source, BSD license) • Effort started at Boston University in 2008, now in wide use as the GPU backend for BQCD, Chroma, CPS, MILC, TIFR, etc. • Provides: — Various solvers for all major fermionic discretizations, with multi-GPU support — Additional performance-critical routines needed for gauge-field generation • Maximize performance – Exploit physical symmetries to minimize memory traffic – Mixed-precision methods – Autotuning for high performance on all CUDA-capable architectures – Domain-decomposed (Schwarz) preconditioners for strong scaling – Eigenvector and deflated solvers (Lanczos, EigCG, GMRES-DR) – Multi-source solvers – Multigrid solvers for optimal convergence • A research tool for how to reach the exascale !10 QUDA CONTRIBUTORS 10 years - lots of contributors § Ron Babich (NVIDIA) § Dean Howarth (BU) § Simone Bacchio (Cyprus) § Bálint Joó (Jlab) § Michael Baldhauf (Regensburg) § Hyung-Jin Kim (BNL -> Samsung) § Kip Barros (LANL) § Bartek Kostrzewa (Bonn) § Rich Brower (Boston University) § Claudio Rebbi (Boston University) § Nuno Cardoso (NCSA) § Hauke Sandmeyer (Bielefeld) § Kate Clark (NVIDIA)* § Guochun Shi (NCSA -> Google) § Michael Cheng (Boston University) § Mario Schröck (INFN) § Carleton DeTar (Utah University) § Alexei Strelchenko (FNAL) § Justin Foley (Utah -> NIH) § Jiqun Tu (Columbia) § Joel Giedt (Rensselaer Polytechnic Institute) § Alejandro Vaquero (Utah University) § Arjun Gambhir (William and Mary) § Mathias Wagner (NVIDIA)* § Steve Gottlieb (Indiana University) § Evan Weinberg (NVIDIA)* *this work § Kyriakos Hadjiyiannakou (Cyprus) § Frank Winter (Jlab) !11 LINEAR SOLVERS while (|rk|> ε) { •βk = (rk,rk)/(rk-1,rk-1) •pk+1 = rk - βkpk qk+1 = A pk+1 QUDA supports a wide range of linear solvers •α = (rk,rk)/(pk+1, qk+1) •r = r - αq CG, BiCGstab, GCR, Multi-shift solvers, etc. k+1 k k+1 •xk+1 = xk + αpk+1 •k = k+1 } Condition number inversely proportional to mass Light (realistic) masses are highly singular conjugate gradient Naive Krylov solvers suffer from critical slowing down at decreasing mass Entire solver algorithm must run on GPUs Time-critical kernel is the stencil application Also require BLAS level-1 type operations !12 MAPPING THE DIRAC OPERATOR TO CUDA review basic details of the LQCD application and of NVIDIA x GPU hardware. We then briefly consider some related work in Section IV before turning to a general description of the QUDA library in Section V. Our parallelization of the quark U interaction matrix is described in VI, and we present and x discuss our performance data for the parallelized solver in • Finite difference operator in LQCDSection is VII. known We finish as with Dslash conclusions and aD discussionx,x of = 0 x x future work in Section VIII. − x U μ • Assign a single space-time point to each thread x II. LATTICE QCD ν 4 6 V = XYZT threads, e.g., V = 24 =>The 3.3x10 necessity forthreads a lattice discretized formulation of QCD μ arises due to the failure of perturbative approaches commonly x− • Looping over direction each threadused for must calculations in other quantum field theories, such as electrodynamics. Quarks, the fundamental particles that are at – Load the neighboring spinor (24 numbers x8) Fig. 1. The nearest neighbor stencil part of the lattice Dirac operator D, the heart of QCD, are described by the Dirac operator acting as defined in (2), in the µ ⇥ plane. The color-spinor fields are located on − µ – Load the color matrix connectingin the the presence sites of (18 a local numbers SU(3) symmetry. x8) On the lattice, the sites. The SU(3) color matrices Ux are associated with the links. The the Dirac operator becomes a large sparse matrix, M, and the nearest neighbor nature of the stencil suggests a natural even-odd (red-black) Do the computation coloring for the sites. – calculation of quark physics is essentially reduced to many – Save the result (24 numbers) solutions to systems of linear equations given by X[1] Mx = b. (1) as red-black) preconditioning is used to accelerate the solution • Each thread has (Wilson Dslash) 0.92 naive arithmetic intensity finding process, where the nearest neighbor property of the The form of M on which we focus in this work is the Dx,x0 matrix (see Fig. 1) is exploited to solve the Schur com- • QUDA reduces memory traffic Sheikholeslami-Wohlert [6] (colloquially known as Wilson- plement system [9]. This has no effect on the overall efficiency Exact SU(3) matrix compressionclover (18) form,=> 12 which or is 8 a centralreal numbers) difference discretization of the since the fields are reordered such that all components of Dirac operator. When acting in a vector space that is the tensor a given parity are contiguous. The quark mass controls the Use 16-bit fixed-point representationproduct of with a 4-dimensional mixed-precision discretized Euclidean solver spacetime, condition number of the matrix, and hence the convergence of spin space, and color space it is given by such iterative solvers.X[0] Unfortunately, physical quark masses 4 correspond to nearly indefinite matrices.!13 Given that current 1 µ µ +µ µ † 3 8 Mx,x0 = P − Ux δx+ˆµ,x0 + P Ux µˆ δx µ,xˆ 0 leading lattice volumes are 32 256, for > 10 degrees of −2 ⇤ ⇤ − − ⇥ µ=1 freedom in total, this represents an extremely computationally ⇤ ⇥ +(4+m + Ax)δx,x0 demanding task. 1 D +(4+m + A )δ . (2) III. GRAPHICS PROCESSING UNITS ⌅2 x,x0 x x,x0 µ In the context of general-purpose computing, a GPU is Here δ is the Kronecker delta; P ± are 4 4 matrix x,y ⇥ effectively an independent parallel processor with its own projectors in spin space; U is the QCD gauge field which locally-attached memory, herein referred to as device memory. is a field of special unitary 3 3 (i.e., SU(3)) matrices acting ⇥ The GPU relies on the host, however, to schedule blocks of in color space that live between the spacetime sites (and hence code (or kernels) for execution, as well as for I/O. Data is are referred to as link matrices); Ax is the 12 12 clover matrix 1⇥ exchanged between the GPU and the host via explicit memory field acting in both spin and color space, corresponding to copies, which take place over the PCI-Express bus. The low- a first order discretization correction; and m is the quark level details of the data transfers, as well as management of mass parameter. The indices x and x0 are spacetime indices the execution environment, are handled by the GPU device (the spin and color indices have been suppressed for brevity).
Load more

Recommended publications
  • Energy-Efficient VLSI Architectures for Next
    UNIVERSITY OF CALIFORNIA Los Angeles Energy-Efficient VLSI Architectures for Next- Generation Software-Defined and Cognitive Radios A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Electrical Engineering by Fang-Li Yuan 2014 c Copyright by Fang-Li Yuan 2014 ABSTRACT OF THE DISSERTATION Energy-Efficient VLSI Architectures for Next- Generation Software-Defined and Cognitive Radios by Fang-Li Yuan Doctor of Philosophy in Electrical Engineering University of California, Los Angeles, 2014 Professor Dejan Markovic,´ Chair Dedicated radio hardware is no longer promising as it was in the past. Today, the support of diverse standards dictates more flexible solutions. Software-defined radio (SDR) provides the flexibility by replacing dedicated blocks (i.e. ASICs) with more general processors to adapt to various functions, standards and even allow mutable de- sign changes. However, such replacement generally incurs significant efficiency loss in circuits, hindering its feasibility for energy-constrained devices. The capability of dy- namic and blind spectrum analysis, as featured in the cognitive radio (CR) technology, makes chip implementation even more challenging. This work discusses several design techniques to achieve near-ASIC energy effi- ciency while providing the flexibility required by software-defined and cognitive radios. The algorithm-architecture co-design is used to determine domain-specific dataflow ii structures to achieve the right balance between energy efficiency and flexibility. The flexible instruction-set-architecture (ISA), the multi-scale interconnects, and the multi- core dynamic scheduling are also proposed to reduce the energy overhead. We demon- strate these concepts on two real-time blind classification chips for CR spectrum anal- ysis, as well as a 16-core processor for baseband SDR signal processing.
    [Show full text]
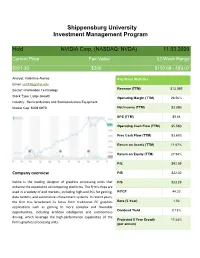
  • Shippensburg University Investment Management Program
    Shippensburg University Investment Management Program Hold NVIDIA Corp. (NASDAQ: NVDA) 11.03.2020 Current Price Fair Value 52 Week Range $501.36 $300 $180.68 - 589.07 Analyst: Valentina Alonso Key Stock Statistics Email: [email protected] Sector: Information Technology Revenue (TTM) $13.06B Stock Type: Large Growth Operating Margin (TTM) 28.56% Industry: Semiconductors and Semiconductors Equipment Market Cap: $309.697B Net Income (TTM) $3.39B EPS (TTM) $5.44 Operating Cash Flow (TTM) $5.58B Free Cash Flow (TTM) $3.67B Return on Assets (TTM) 11.67% Return on Equity (TTM) 27.94% P/E $92.59 Company overview P/B $22.32 Nvidia is the leading designer of graphics processing units that P/S $23.29 enhance the experience on computing platforms. The firm's chips are used in a variety of end markets, including high-end PCs for gaming, P/FCF 44.22 data centers, and automotive infotainment systems. In recent years, the firm has broadened its focus from traditional PC graphics Beta (5-Year) 1.54 applications such as gaming to more complex and favorable Dividend Yield 0.13% opportunities, including artificial intelligence and autonomous driving, which leverage the high-performance capabilities of the Projected 5 Year Growth 17.44% firm's graphics processing units. (per annum) Contents Executive Summary ....................................................................................................................................................3 Company Overview ....................................................................................................................................................4
    [Show full text]
  • Manycore GPU Architectures and Programming, Part 1
    Lecture 19: Manycore GPU Architectures and Programming, Part 1 Concurrent and Mul=core Programming CSE 436/536, [email protected] www.secs.oakland.edu/~yan 1 Topics (Part 2) • Parallel architectures and hardware – Parallel computer architectures – Memory hierarchy and cache coherency • Manycore GPU architectures and programming – GPUs architectures – CUDA programming – Introduc?on to offloading model in OpenMP and OpenACC • Programming on large scale systems (Chapter 6) – MPI (point to point and collec=ves) – Introduc?on to PGAS languages, UPC and Chapel • Parallel algorithms (Chapter 8,9 &10) – Dense matrix, and sorng 2 Manycore GPU Architectures and Programming: Outline • Introduc?on – GPU architectures, GPGPUs, and CUDA • GPU Execuon model • CUDA Programming model • Working with Memory in CUDA – Global memory, shared and constant memory • Streams and concurrency • CUDA instruc?on intrinsic and library • Performance, profiling, debugging, and error handling • Direc?ve-based high-level programming model – OpenACC and OpenMP 3 Computer Graphics GPU: Graphics Processing Unit 4 Graphics Processing Unit (GPU) Image: h[p://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 5 Graphics Processing Unit (GPU) • Enriching user visual experience • Delivering energy-efficient compung • Unlocking poten?als of complex apps • Enabling Deeper scien?fic discovery 6 What is GPU Today? • It is a processor op?mized for 2D/3D graphics, video, visual compu?ng, and display. • It is highly parallel, highly multhreaded mulprocessor op?mized for visual
    [Show full text]
  • Lecture: Manycore GPU Architectures and Programming, Part 1
    Lecture: Manycore GPU Architectures and Programming, Part 1 CSCE 569 Parallel Computing Department of Computer Science and Engineering Yonghong Yan [email protected] https://passlab.github.io/CSCE569/ 1 Manycore GPU Architectures and Programming: Outline • Introduction – GPU architectures, GPGPUs, and CUDA • GPU Execution model • CUDA Programming model • Working with Memory in CUDA – Global memory, shared and constant memory • Streams and concurrency • CUDA instruction intrinsic and library • Performance, profiling, debugging, and error handling • Directive-based high-level programming model – OpenACC and OpenMP 2 Computer Graphics GPU: Graphics Processing Unit 3 Graphics Processing Unit (GPU) Image: http://www.ntu.edu.sg/home/ehchua/programming/opengl/CG_BasicsTheory.html 4 Graphics Processing Unit (GPU) • Enriching user visual experience • Delivering energy-efficient computing • Unlocking potentials of complex apps • Enabling Deeper scientific discovery 5 What is GPU Today? • It is a processor optimized for 2D/3D graphics, video, visual computing, and display. • It is highly parallel, highly multithreaded multiprocessor optimized for visual computing. • It provide real-time visual interaction with computed objects via graphics images, and video. • It serves as both a programmable graphics processor and a scalable parallel computing platform. – Heterogeneous systems: combine a GPU with a CPU • It is called as Many-core 6 Graphics Processing Units (GPUs): Brief History GPU Computing General-purpose computing on graphics processing units (GPGPUs) GPUs with programmable shading Nvidia GeForce GE 3 (2001) with programmable shading DirectX graphics API OpenGL graphics API Hardware-accelerated 3D graphics S3 graphics cards- single chip 2D accelerator Atari 8-bit computer IBM PC Professional Playstation text/graphics chip Graphics Controller card 1970 1980 1990 2000 2010 Source of information http://en.wikipedia.org/wiki/Graphics_Processing_Unit 7 NVIDIA Products • NVIDIA Corp.
    [Show full text]
  • Cuda-Gdb Cuda Debugger
    CUDA-GDB CUDA DEBUGGER DU-05227-042 _v5.0 | October 2012 User Manual TABLE OF CONTENTS Chapter 1. Introduction.........................................................................................1 1.1 What is CUDA-GDB?...................................................................................... 1 1.2 Supported Features...................................................................................... 1 1.3 About This Document.................................................................................... 2 Chapter 2. Release Notes...................................................................................... 3 Chapter 3. Getting Started.....................................................................................6 3.1 Installation Instructions..................................................................................6 3.2 Setting Up the Debugger Environment................................................................6 3.2.1 Linux...................................................................................................6 3.2.2 Mac OS X............................................................................................. 6 3.2.3 Temporary Directory................................................................................ 7 3.3 Compiling the Application...............................................................................8 3.3.1 Debug Compilation.................................................................................. 8 3.3.2 Compiling for Fermi GPUs........................................................................
    [Show full text]
  • GPU Architecture:Architecture: Implicationsimplications && Trendstrends
    GPUGPU Architecture:Architecture: ImplicationsImplications && TrendsTrends DavidDavid Luebke,Luebke, NVIDIANVIDIA ResearchResearch Beyond Programmable Shading: In Action GraphicsGraphics inin aa NutshellNutshell • Make great images – intricate shapes – complex optical effects – seamless motion • Make them fast – invent clever techniques – use every trick imaginable – build monster hardware Eugene d’Eon, David Luebke, Eric Enderton In Proc. EGSR 2007 and GPU Gems 3 …… oror wewe couldcould justjust dodo itit byby handhand Perspective study of a chalice Paolo Uccello, circa 1450 Beyond Programmable Shading: In Action GPU Evolution - Hardware 1995 1999 2002 2003 2004 2005 2006-2007 NV1 GeForce 256 GeForce4 GeForce FX GeForce 6 GeForce 7 GeForce 8 1 Million 22 Million 63 Million 130 Million 222 Million 302 Million 754 Million Transistors Transistors Transistors Transistors Transistors Transistors Transistors 20082008 GeForceGeForce GTX GTX 200200 1.41.4 BillionBillion TransistorsTransistors Beyond Programmable Shading: In Action GPUGPU EvolutionEvolution -- ProgrammabilityProgrammability ? Future: CUDA, DX11 Compute, OpenCL CUDA (PhysX, RT, AFSM...) 2008 - Backbreaker DX10 Geo Shaders 2007 - Crysis DX9 Prog Shaders 2004 – Far Cry DX7 HW T&L DX8 Pixel Shaders 1999 – Test Drive 6 2001 – Ballistics TheThe GraphicsGraphics PipelinePipeline Vertex Transform & Lighting Triangle Setup & Rasterization Texturing & Pixel Shading Depth Test & Blending Framebuffer Beyond Programmable Shading: In Action TheThe GraphicsGraphics PipelinePipeline Vertex Transform
    [Show full text]
  • Cinefx Architecture Siggraph 2002 NV1 SEGA Virtua Fighter 50K Polygons/Sec 1M Pixel Ops/Sec Circa 1995
    CineFX Architecture Siggraph 2002 NV1 SEGA Virtua Fighter 50K polygons/sec 1M pixel ops/sec Circa 1995 NVIDIA CONFIDENTIAL XBOX 100MPolys/sec 1G pixel ops/sec Circa 2001 NVIDIA CONFIDENTIAL Convergence of Film and Real-time Rendering NVIDIA CONFIDENTIAL CinematicCinematic ShadingShading Final Fantasy NVIDIA CONFIDENTIAL The Spirits Within Square Real-time Cinematic Shading requires new levels of features and performance • Advanced Programmability • High-precision color • High-level Shading Language • Highly efficient architecture • High bandwidth to system memory and CPU NVIDIA CONFIDENTIAL Artist: Count Love Introducing the CineFX Architecture Generalized Vertex Processing Generalized Pixel Processing 128-bit Floating Point Precision Highly advanced rendering architecture Dramatically improved performance NVIDIA CONFIDENTIAL CineFX Generalized Vertex Processing DX8.0 R300 CineFX Up to 65536 vertex Vertex Shaders 1.1 2.0 2.0+ Max Instructions 128 1024 65536 instructions Max Static Instructions 128 256 256 Max. Constants 96 256 256 256 constants Temporary Registers 12 12 16 Loops & Branching Max Loops 0 4 256 Conditional Write Masks - - ü Forward & backwards Call & Return - - ü Static Flow Control - ü ü Data Dependent Dynamic Flow Control - - ü Call & Return - Subroutines Per component condition codes & write masks Faster than branching for short basic blocks NVIDIA CONFIDENTIAL CineFX Vertex Processing Instruction Set Add & multiply instructions ADD, DP3, DP4, DPH, MAD, MOV, SUB Math functions ABS, COS, EX2, EXP, FLR, FRC, LG2, LOG, RCP,
    [Show full text]
  • Your Graphic Designer
    Monday-Friday 9am-6pm Holiday/Weekend Closed (619) 425-5592 We Custom Built Computers PC . Upgrade . Fix Probems. Remove Virus Free No Obligation Computer Diagnostic | Free Upgrade Consultation ON-SALE : $995.00 Asus ExpertBook P2451FA-XS74 (14 inch) Intel Core i7-10510U 1.8GHz up to 4.9 GHz Memory 16GB DDR4 (On-Board) SSD 512GB PCIE SSD + TPM Operating System Windows 10 Professional Webcam HD IR Camera Illuminated Chiclet Keyboard with Track Point Add $149 : Microso� Office Home/Student Classic 2019 versions of Word, Excel and PowerPoint. Plus OneNote Add $239 : Microso� Office Home/Business Classic 2019 versions of Word, Excel, PowerPoint, and Outlook Add $115 : Microso� Windows 10 Home Add $139 : Microso� Windows 10 Pro In-Win Case Add $26.00 Custom Ul�mate Performance PC Custom AMD The Elite Gaming PC SSD 1TB NVMe M.2 Solid State Price $1159.00: ON SALE! Custom Pro PC : Home/Business Memory Kingston 16GB DDR4-3600 DEEPCOOL Mid Tower 3-Fans RGB $1059.00 SSD 500GB NVMe M.2 Solid State EVGA Super NOVA GOLD 650W SPU Processor Ryzen 5 3600 6-Core 3.6GHz SSD 500GB NVMe M.2 Solid State Memory Kingston 16GB DDR4-2666 Gigabyte Intel Z590 Motherboard SuperCase w/ 300W SPU Integrated Graphics, Ethernet, audio Memory Kingston 16GB DDR4-3200 Antec NX400 NX Gaming Case Asus Intel B460M Motherboard Intel Core i5-11600K 3.9GHz : $1090.00 EVGA Super NOVA GOLD 650W SPU Integrated Graphics, Ethernet, audio Asus B550M-A WiFi Motherboard Intel i5 2.9GHz Six-Core : $645.00 Intel Core i7-11700K 3.6GHz : $1223.00 Graphic nVidia GTX 1050 Ti OC 4GB Intel Core i9-11900K 3.5GHz : $1440.00 OS: Windows 10 Home 64bit Intel i7 2.5GHz Eight-Core : $845.00 Best Deal Computer Services, Inc.
    [Show full text]
  • Linux Hardware Compatibility HOWTO
    Linux Hardware Compatibility HOWTO Steven Pritchard Southern Illinois Linux Users Group / K&S Pritchard Enterprises, Inc. <[email protected]> 3.2.4 Copyright © 2001−2007 Steven Pritchard Copyright © 1997−1999 Patrick Reijnen 2007−05−22 This document attempts to list most of the hardware known to be either supported or unsupported under Linux. Copyright This HOWTO is free documentation; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free software Foundation; either version 2 of the license, or (at your option) any later version. Linux Hardware Compatibility HOWTO Table of Contents 1. Introduction.....................................................................................................................................................1 1.1. Notes on binary−only drivers...........................................................................................................1 1.2. Notes on proprietary drivers.............................................................................................................1 1.3. System architectures.........................................................................................................................1 1.4. Related sources of information.........................................................................................................2 1.5. Known problems with this document...............................................................................................2 1.6. New versions of this document.........................................................................................................2
    [Show full text]
  • NVIDIA Opengl Extension Specifications
    NVIDIA OpenGL Extension Specifications NVIDIA OpenGL Extension Specifications NVIDIA Corporation Mark J. Kilgard, editor [email protected] May 21, 2001 1 NVIDIA OpenGL Extension Specifications Copyright NVIDIA Corporation, 1999, 2000, 2001. This document is protected by copyright and contains information proprietary to NVIDIA Corporation as designated in the document. Other OpenGL extension specifications can be found at: http://oss.sgi.com/projects/ogl-sample/registry/ 2 NVIDIA OpenGL Extension Specifications Table of Contents Table of NVIDIA OpenGL Extension Support.............................. 4 ARB_imaging........................................................... 6 ARB_multisample....................................................... 7 ARB_multitexture..................................................... 18 ARB_texture_border_clamp............................................. 19 ARB_texture_compression.............................................. 25 ARB_texture_cube_map................................................. 48 ARB_texture_env_add.................................................. 62 ARB_texture_env_combine.............................................. 65 ARB_texture_env_dot3................................................. 73 ARB_transpose_matrix................................................. 76 EXT_abgr............................................................. 81 EXT_bgra............................................................. 84 EXT_blend_color...................................................... 86 EXT_blend_minmax....................................................
    [Show full text]
  • NVIDIA Topology-Aware GPU Selection 0.1.0 (Early Access)
    NVIDIA Topology-Aware GPU Selection 0.1.0 (Early Access) User Guide DU-09998-001_v0.1.0 (Early Access) | July 2020 Table of Contents Chapter 1. Introduction........................................................................................................ 1 Chapter 2. Getting Started................................................................................................... 4 2.1. Prerequisites............................................................................................................................. 4 2.2. Installing NVTAGS..................................................................................................................... 4 Chapter 3. Using NVTAGS.................................................................................................... 6 3.1. NVTAGS Tune Mode..................................................................................................................6 3.1.1. Tune with profiling............................................................................................................. 6 3.1.2. Run NVTAGS in Tune with Profiling Mode........................................................................7 3.2. Tune NVTAGS without Profiling Mode..................................................................................... 7 3.2.1. Run NVTAGS in Tune without Profiling Mode...................................................................7 3.3. NVTAGS Run Mode..................................................................................................................
    [Show full text]
  • John Carmack Archive - Interviews
    John Carmack Archive - Interviews http://www.team5150.com/~andrew/carmack August 2, 2008 Contents 1 John Carmack Interview5 2 John Carmack - The Boot Interview 12 2.1 Page 1............................... 13 2.2 Page 2............................... 14 2.3 Page 3............................... 16 2.4 Page 4............................... 18 2.5 Page 5............................... 21 2.6 Page 6............................... 22 2.7 Page 7............................... 24 2.8 Page 8............................... 25 3 John Carmack - The Boot Interview (Outtakes) 28 4 John Carmack (of id Software) interview 48 5 Interview with John Carmack 59 6 Carmack Q&A on Q3A changes 67 1 John Carmack Archive 2 Interviews 7 Carmack responds to FS Suggestions 70 8 Slashdot asks, John Carmack Answers 74 9 John Carmack Interview 86 9.1 The Man Behind the Phenomenon.............. 87 9.2 Carmack on Money....................... 89 9.3 Focus and Inspiration...................... 90 9.4 Epiphanies............................ 92 9.5 On Open Source......................... 94 9.6 More on Linux.......................... 95 9.7 Carmack the Student...................... 97 9.8 Quake and Simplicity...................... 98 9.9 The Next id Game........................ 100 9.10 On the Gaming Industry.................... 101 9.11 id is not a publisher....................... 103 9.12 The Trinity Thing........................ 105 9.13 Voxels and Curves........................ 106 9.14 Looking at the Competition.................. 108 9.15 Carmack’s Research......................
    [Show full text]