DOCSLIB.ORG

Discrete Simulation of Colored Noise and Stochastic Processes and 1/F

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Discrete Simulation of Colored Noise and Stochastic Processes and 1/F Discrete Simulation of Colored Noise and Stochastic Processes and llf" Power Law Noise Generation ~ ~ N. JEREMY USDIN, MEMBER, IEEE This paper discusses techniquesfor generating digital sequences [lo], [121-[14], [271, 1341, P71, [391, [411, [441, of noise which simulate processes with certain known properties [531, [541, [571, [581, [@I, 1681, [@I, [731-[751, [771, [791. or describing equations. Part I of the paper presents a review This paper discusses the theory and mechanics of gen- of stochastic processes and spectral estimation (with some new results) and a tutorial on simulating continuous noise processes erating digital, pseudorandom sequences on a computer with a known autospectral density or autocorrelation function. In as simulations of known stochastic processes. In other defining these techniques for computer generating sequences, it words, given the autospectral density or autocorrelation of also defines the necessary accuracy criteria. These methods are a process or a differential equation describing a system, compared to some of the common techniques for noise generation methods are presented for producing digital sequences with and the problems, or advantages, of each are discussed. Finally, Part I presents results on simulating stochastic differential equa- the "correct" discrete spectrum or correlations. The precise tions. A Runge-Kutta (RK) method is presented for numerically meaning of correct is discussed but can vary depending solving these equations. upon the specific application. Though many new results are Part I1 of the paper discusses power law, or 1/ f a, noises. Such reported, particularly in the area of nonlinear differential noise processes occur frequently in nature and, in many cases, with equation integration and power law noise simulation, this nonintegral values for a. A review of 1/ f noises in devices and systems is followed by a discussion of the most common continuous paper is also intended as a tutorial on colored noise analysis 1/ f noise models. The paper then presents a new dim1 model for and generation. Thus the detailed proofs or derivations are power law noises. This model allows for very accurate and efficient omitted or referred to cited works. computer generation of l/f" noises for any a. Many of the The paper is divided into two parts. The first discusses statistical properties of this model are discussed and compared to the previous continuous models. Lastly, a number of approximate the general problem of simulating stochastic processes on techniquesfor generating power law noises are presented for rapid a computer. Some time is spent defining what is meant by or real time simulation. a stochastic simulation and criteria are presented for eval- uating the effectiveness of a generation method. Some past I. INTRODUCTION techniques, particularly those involving direct simulation in the frequency domain from given spectra, are reviewed The need for accurate simulation of stochastic processes with an eye toward pointing out some of their deficiencies. and stochastic differential equations arises across almost Part I presents two techniques for simulating noise with a all disciplines of science and engineering. Mechanical and given spectra or autocorrelation function-a time domain aerospace engineers often simulate complex, nonlinear and frequency domain method. In addition, a RK algorithm models of dynamic systems acted upon by noise. In for simulating general, nonlinear, inhomogeneous stochastic electrical engineering and physics it is common to simulate differential equations is reviewed. various types of colored noises as models for sensors The second part focuses on the problem of generating and actuators. There are numerous nonlinear systems sequences of power law or l/f" noises (also often called arising in all areas of physics that require techniques for fractal processes). This is a remarkably ubiquitous prob- simulating stochastic differential equations. And the timing lem spanning innumerable fields, from music and to community has a long history of simulation for modeling art hydrology and low temperature physics. Countless devices phase and frequency noise in oscillators [2], [4], [5], [8], and systems have been seen to produce noises with an Manuscript received August 9, 1993; revised January 30, 1995. This autospectral density proportional to f-" with f the cyclic work was supported by NASA Contract NAS8-36125. frequency and a a real number between 0 and 2. Many The author is with the W.W. Hansen Experimental Physics Laboratory, models and techniques have been proposed in the past Relativity MissiodGravity Probe B, Stanford University, Stanford, CA 94305-4085 USA. to simulate these noises. Because the spectrum is not IEEE Log Number 9410317. rational, it is impossible to use standard linear system 0018-9219/95$04.00 0 1995 IEEE 802 PROCEEDINGS OF THE IEEE, VOL. 83, NO. 5, MAY 1995 - theory and differential equation models to simulate the In most cases, and all those in this paper, only the first noise via the techniques in Part I. Thus in Part 11, after and second order properties of the process are desired rather a review of past generation techniques, a new model is than the complete joint distribution function. For Gaussian proposed. This model, first proposed by Hosking [31] and processes, these second order properties completely define later independently by the author, can be used to generate the process distribution. These properties are defined via digital sequences of l/fa noise. The properties of this the following equations: model are discussed in some detail as well as the advantages it has as a generating mechanism over previous methods. In particular, it can be used over a frequency band of arbitrary J -00 size and it is strictly scale invariant. Because noise simulation spreads over so many diverse where q is the mean value of the process and the notation disciplines, it is difficult to find a notation agreeable to all E{ } refers to the expected value operation taken over the participants. This paper, therefore, uses common engineer- ensemble of processes {z(t,C)}. ing notation and methodology for the stochastic process The two-time autocorrelation of the process is given by and system theory discussions. This notation is consistent with that used in [9], [14], [33], [52], [62]. Discussions of discrete system theory and the a-transform can be found in [231, 1511, [521. PART I: STOCHASTIC PROCESS SIMULATION The autocovariance is defined by 11. REVIEW AND DEFINITIONS (Note that all processes in this paper are real). Before embarking on the detailed discussion of noise Thus, the variance of the process, a2(t),is given by simulation, it is useful to review some fundamentals of C(t,t). For this paper, all processes will be assumed zero stochastic process theory and noise measurements. This mean so that the autocorrelation and autocovariance are section presents background information and definitions as well as some new, and important, results in stochastic identical. process analysis and spectral measurement and estimation In general, the moments of a stochastic process defined in that will form the foundation for the simulation techniques (2) and (3) vary with time. However, a stationary process discussed in Section 111. The review material in this section is defined as one whose density function is invariant to follows the presentation in [52]. Further reading can be time shifts and thus independent of the times tl,tz, . ,t,. found in [9], [26], [62], [70], [74]. Much of the information Such a process is called strict-sense stationary. A wide- on spectral density measurements and estimation can also sense stationary process is one whose first and second order be found in [9]. properties only are independent of time, that is, q(t) = q, and R(t1,tz)= R(t1 - tz). A. Stochastic Processes For stationary processes the autocorrelation function def- It is assumed that the reader is familiar with the funda- inition is often written in the asymmetric form: mental axioms of probability and basic random variables. If we are given the probability space (R,7,F), then the stochastic process z(t)is defined in [52] as follows: "z(t,C) is a stochastic process when the random variable The variance of the process is then given by R(0). z represents the value of the outcome < of an experiment Since we will be dealing with many nonstationary and 7 for every time t," where R represents the sample space, transient processes, it is more convenient to use a symmetric 7 the event space or sigma algebra, and F the probability definition of the autocorrelation function: measure [26]. Normally, the dependence upon the event space, C, is omitted and the stochastic process is written as z(t).If the probability distribution function for z is given by F(z), For stationary processes, (6) and (5) give the same result. then we can define the general nth order, time-varying, However, when we later compute spectra and other prop- erties of nonstationary processes, (6) will be necessary in joint distribution function, F(z1,.. ,z,; tl,. , tn), for the random variables z(tl),. ,z(tn). The joint probability order to achieve consistent and accurate results. density function is then given by This distinction is important as we consider noise gen- eration. In simulation, we must be concerned with the transients of processes, thus implying that all signals under consideration for simulation will be nonstationary. How- ever, we can define an asymptotically stationary process as KASDIN DISCRETE SIMULATION OF COLORED NOISE AND STOCHASTIC PROCESSES 803 ~~ ~ - __ - one whose autocorrelation function satisfies: It is straightforward to show from this that Brown- ian motion is a nonstationary process with symmetric lim R(~,T)= R(T). (7) t+m autocorrelation: Many of the process models used for simulation will be asymptotically stationary. RB(t,r)= Q(1- 7). Lastly, it is useful to have a measure of the “memory” of a process.
Load more

Recommended publications
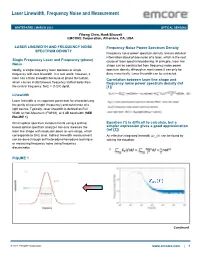
  • Laser Linewidth, Frequency Noise and Measurement
    Laser Linewidth, Frequency Noise and Measurement WHITEPAPER | MARCH 2021 OPTICAL SENSING Yihong Chen, Hank Blauvelt EMCORE Corporation, Alhambra, CA, USA LASER LINEWIDTH AND FREQUENCY NOISE Frequency Noise Power Spectrum Density SPECTRUM DENSITY Frequency noise power spectrum density reveals detailed information about phase noise of a laser, which is the root Single Frequency Laser and Frequency (phase) cause of laser spectral broadening. In principle, laser line Noise shape can be constructed from frequency noise power Ideally, a single frequency laser operates at single spectrum density although in most cases it can only be frequency with zero linewidth. In a real world, however, a done numerically. Laser linewidth can be extracted. laser has a finite linewidth because of phase fluctuation, Correlation between laser line shape and which causes instantaneous frequency shifted away from frequency noise power spectrum density (ref the central frequency: δν(t) = (1/2π) dφ/dt. [1]) Linewidth Laser linewidth is an important parameter for characterizing the purity of wavelength (frequency) and coherence of a Graphic (Heading 4-Subhead Black) light source. Typically, laser linewidth is defined as Full Width at Half-Maximum (FWHM), or 3 dB bandwidth (SEE FIGURE 1) Direct optical spectrum measurements using a grating Equation (1) is difficult to calculate, but a based optical spectrum analyzer can only measure the simpler expression gives a good approximation laser line shape with resolution down to ~pm range, which (ref [2]) corresponds to GHz level. Indirect linewidth measurement An effective integrated linewidth ∆_ can be found by can be done through self-heterodyne/homodyne technique solving the equation: or measuring frequency noise using frequency discriminator.
    [Show full text]
  • Tm Synchronization and Channel Coding—Summary of Concept and Rationale
    Report Concerning Space Data System Standards TM SYNCHRONIZATION AND CHANNEL CODING— SUMMARY OF CONCEPT AND RATIONALE INFORMATIONAL REPORT CCSDS 130.1-G-3 GREEN BOOK June 2020 Report Concerning Space Data System Standards TM SYNCHRONIZATION AND CHANNEL CODING— SUMMARY OF CONCEPT AND RATIONALE INFORMATIONAL REPORT CCSDS 130.1-G-3 GREEN BOOK June 2020 TM SYNCHRONIZATION AND CHANNEL CODING—SUMMARY OF CONCEPT AND RATIONALE AUTHORITY Issue: Informational Report, Issue 3 Date: June 2020 Location: Washington, DC, USA This document has been approved for publication by the Management Council of the Consultative Committee for Space Data Systems (CCSDS) and reflects the consensus of technical panel experts from CCSDS Member Agencies. The procedure for review and authorization of CCSDS Reports is detailed in Organization and Processes for the Consultative Committee for Space Data Systems (CCSDS A02.1-Y-4). This document is published and maintained by: CCSDS Secretariat National Aeronautics and Space Administration Washington, DC, USA Email: [email protected] CCSDS 130.1-G-3 Page i June 2020 TM SYNCHRONIZATION AND CHANNEL CODING—SUMMARY OF CONCEPT AND RATIONALE FOREWORD This document is a CCSDS Report that contains background and explanatory material to support the CCSDS Recommended Standard, TM Synchronization and Channel Coding (reference [3]). Through the process of normal evolution, it is expected that expansion, deletion, or modification of this document may occur. This Report is therefore subject to CCSDS document management and change control procedures, which are defined in Organization and Processes for the Consultative Committee for Space Data Systems (CCSDS A02.1-Y-4). Current versions of CCSDS documents are maintained at the CCSDS Web site: http://www.ccsds.org/ Questions relating to the contents or status of this document should be sent to the CCSDS Secretariat at the email address indicated on page i.
    [Show full text]
  • 10S Johnson-Nyquist Noise Masatsugu Sei Suzuki Department of Physics, SUNY at Binghamton (Date: January 02, 2011)
    Chapter 10S Johnson-Nyquist noise Masatsugu Sei Suzuki Department of Physics, SUNY at Binghamton (Date: January 02, 2011) Johnson noise Johnson-Nyquist theorem Boltzmann constant Parseval relation Correlation function Spectral density Wiener-Khinchin (or Khintchine) Flicker noise Shot noise Poisson distribution Brownian motion Fluctuation-dissipation theorem Langevin function ___________________________________________________________________________ John Bertrand "Bert" Johnson (October 2, 1887–November 27, 1970) was a Swedish-born American electrical engineer and physicist. He first explained in detail a fundamental source of random interference with information traveling on wires. In 1928, while at Bell Telephone Laboratories he published the journal paper "Thermal Agitation of Electricity in Conductors". In telecommunication or other systems, thermal noise (or Johnson noise) is the noise generated by thermal agitation of electrons in a conductor. Johnson's papers showed a statistical fluctuation of electric charge occur in all electrical conductors, producing random variation of potential between the conductor ends (such as in vacuum tube amplifiers and thermocouples). Thermal noise power, per hertz, is equal throughout the frequency spectrum. Johnson deduced that thermal noise is intrinsic to all resistors and is not a sign of poor design or manufacture, although resistors may also have excess noise. http://en.wikipedia.org/wiki/John_B._Johnson 1 ____________________________________________________________________________ Harry Nyquist (February 7, 1889 – April 4, 1976) was an important contributor to information theory. http://en.wikipedia.org/wiki/Harry_Nyquist ___________________________________________________________________________ 10S.1 Histrory In 1926, experimental physicist John Johnson working in the physics division at Bell Labs was researching noise in electronic circuits. He discovered random fluctuations in the voltages across electrical resistors, whose power was proportional to temperature.
    [Show full text]
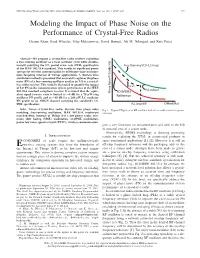
  • Modeling the Impact of Phase Noise on the Performance of Crystal-Free Radios Osama Khan, Brad Wheeler, Filip Maksimovic, David Burnett, Ali M
    IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS—II: EXPRESS BRIEFS, VOL. 64, NO. 7, JULY 2017 777 Modeling the Impact of Phase Noise on the Performance of Crystal-Free Radios Osama Khan, Brad Wheeler, Filip Maksimovic, David Burnett, Ali M. Niknejad, and Kris Pister Abstract—We propose a crystal-free radio receiver exploiting a free-running oscillator as a local oscillator (LO) while simulta- neously satisfying the 1% packet error rate (PER) specification of the IEEE 802.15.4 standard. This results in significant power savings for wireless communication in millimeter-scale microsys- tems targeting Internet of Things applications. A discrete time simulation method is presented that accurately captures the phase noise (PN) of a free-running oscillator used as an LO in a crystal- free radio receiver. This model is then used to quantify the impact of LO PN on the communication system performance of the IEEE 802.15.4 standard compliant receiver. It is found that the equiv- alent signal-to-noise ratio is limited to ∼8 dB for a 75-µW ring oscillator PN profile and to ∼10 dB for a 240-µW LC oscillator PN profile in an AWGN channel satisfying the standard’s 1% PER specification. Index Terms—Crystal-free radio, discrete time phase noise Fig. 1. Typical PN plot of an RF oscillator locked to a stable crystal frequency modeling, free-running oscillators, IEEE 802.15.4, incoherent reference. matched filter, Internet of Things (IoT), low-power radio, min- imum shift keying (MSK) modulation, O-QPSK modulation, power law noise, quartz crystal (XTAL), wireless communication.
    [Show full text]
  • Arxiv:2003.13216V1 [Cs.CV] 30 Mar 2020
    Learning to Learn Single Domain Generalization Fengchun Qiao Long Zhao Xi Peng University of Delaware Rutgers University University of Delaware [email protected] [email protected] [email protected] Abstract : Source domain(s) <latexit sha1_base64="glUSn7xz2m1yKGYjqzzX12DA3tk=">AAAB8nicjVDLSsNAFL3xWeur6tLNYBFclaQKdllw47KifUAaymQ6aYdOJmHmRiihn+HGhSJu/Rp3/o2TtgsVBQ8MHM65l3vmhKkUBl33w1lZXVvf2Cxtlbd3dvf2KweHHZNkmvE2S2SieyE1XArF2yhQ8l6qOY1Dybvh5Krwu/dcG5GoO5ymPIjpSIlIMIpW8vsxxTGjMr+dDSpVr+bOQf4mVViiNai894cJy2KukElqjO+5KQY51SiY5LNyPzM8pWxCR9y3VNGYmyCfR56RU6sMSZRo+xSSufp1I6exMdM4tJNFRPPTK8TfPD/DqBHkQqUZcsUWh6JMEkxI8X8yFJozlFNLKNPCZiVsTDVlaFsq/6+ETr3mndfqNxfVZmNZRwmO4QTOwINLaMI1tKANDBJ4gCd4dtB5dF6c18XoirPcOYJvcN4+AY5ZkWY=</latexit> <latexit sha1_base64="9X8JvFzvWSXuFK0x/Pe60//G3E4=">AAACD3icbVDLSsNAFJ3UV62vqks3g0Wpm5LW4mtVcOOyUvuANpTJZNIOnUzCzI1YQv/Ajb/ixoUibt26829M2iBqPTBwOOfeO/ceOxBcg2l+GpmFxaXllexqbm19Y3Mrv73T0n6oKGtSX/iqYxPNBJesCRwE6wSKEc8WrG2PLhO/fcuU5r68gXHALI8MJHc5JRBL/fxhzyMwpEREjQnuAbuD6AI3ptOx43uEy6I+muT6+YJZMqfA86SckgJKUe/nP3qOT0OPSaCCaN0tmwFYEVHAqWCTXC/ULCB0RAasG1NJPKataHrPBB/EioNdX8VPAp6qPzsi4mk99uy4Mtle//US8T+vG4J7ZkVcBiEwSWcfuaHA4OMkHOxwxSiIcUwIVTzeFdMhUYRCHOEshPMEJ98nz5NWpVQ+LlWvq4VaJY0ji/bQPiqiMjpFNXSF6qiJKLpHj+gZvRgPxpPxarzNSjNG2rOLfsF4/wJA4Zw6</latexit> S S : Target domain(s) <latexit sha1_base64="ssITTP/Vrn2uchq9aDxvcfruPQc=">AAACD3icbVDLSgNBEJz1bXxFPXoZDEq8hI2Kr5PgxWOEJAaSEHonnWTI7Owy0yuGJX/gxV/x4kERr169+TfuJkF8FTQUVd10d3mhkpZc98OZmp6ZnZtfWMwsLa+srmXXN6o2iIzAighUYGoeWFRSY4UkKayFBsH3FF57/YvUv75BY2WgyzQIselDV8uOFECJ1MruNnygngAVl4e8QXhL8Rkvg+ki8Xbgg9R5uzfMtLI5t+COwP+S4oTk2ASlVva90Q5E5KMmocDaetENqRmDISkUDjONyGIIog9drCdUg4+2GY/+GfKdRGnzTmCS0sRH6veJGHxrB76XdKbX299eKv7n1SPqnDRjqcOIUIvxok6kOAU8DYe3pUFBapAQEEYmt3LRAwOCkgjHIZymOPp6+S+p7heKB4XDq8Pc+f4kjgW2xbZZnhXZMTtnl6zEKkywO/bAntizc+88Oi/O67h1ypnMbLIfcN4+ATKRnDE=</latexit>
    [Show full text]
  • What Is Different? Between Impulse Noise and Electrical Fast Transient Burst】
    【What is different? Between Impulse Noise and Electrical Fast Transient Burst】 The Inquiry about "a distinction between an impulse noise simulator (following and our company model INS series) and a Fast transient Burst simulator (following and our company model FNS series)" is one of the major questions in a lot of quries from customers. Herewith the difference is focused and presented. The phenomenon which are reproduced and backgraound Both INS and FNS reproduce phenomenon of back electromotive energy noise which may be generated in ON/OFF of power supply switching (like a gas insulated braker and/or electromagnetism relay, etc.). INS was introduced by Mr. Manohar L.Tandor (at that time worked in I.B.M) as a simulator of the high frequency noise to data processing apparatus in the 1960s, and the computer maker of those days adopted it in the 1970s, and it spread widely. FNS is indicated as a basic standard of the immunity type test which reproduces the malfunction by the noise phenomenon of switching ON/OFF and adopted not only in Europe but also world-wide. The 1st edition of Standard for this test was issued as IEC801-4 in IEC TC65 (Industrial Process Controls) in 1988. Then, in order to adopt to all the electric devices, IEC1000-4-4 was issued in 1995. Moreover, in order to differenciate the numbering between ISO and IEC, “60000” has been added to the Stadanrd number. Consequently, it has been named as IEC61000-4-4. output waveform Rise time / the pulse width [INS] It is a rectangular wave whose pulse width is 50ns-1μs and rise time is less than 1ns.
    [Show full text]
  • Improved 1/F Noise Measurements for Microwave Transistors Clemente Toro Jr
    University of South Florida Scholar Commons Graduate Theses and Dissertations Graduate School 6-25-2004 Improved 1/f Noise Measurements for Microwave Transistors Clemente Toro Jr. University of South Florida Follow this and additional works at: https://scholarcommons.usf.edu/etd Part of the American Studies Commons Scholar Commons Citation Toro, Clemente Jr., "Improved 1/f Noise Measurements for Microwave Transistors" (2004). Graduate Theses and Dissertations. https://scholarcommons.usf.edu/etd/1271 This Thesis is brought to you for free and open access by the Graduate School at Scholar Commons. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Scholar Commons. For more information, please contact [email protected]. Improved 1/f Noise Measurements for Microwave Transistors by Clemente Toro, Jr. A thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in Electrical Engineering Department of Electrical Engineering College of Engineering University of South Florida Major Professor: Lawrence P. Dunleavy, Ph.D. Thomas Weller, Ph.D. Horace Gordon, Jr., M.S.E., P.E. Date of Approval: June 25, 2004 Keywords: low, frequency, flicker, model, correlation © Copyright 2004, Clemente Toro, Jr. DEDICATION This thesis is dedicated to my father, Clemente, and my mother, Miriam. Thank you for helping me and supporting me throughout my college career! ACKNOWLEDGMENT I would like to acknowledge Dr. Lawrence P. Dunleavy for proving the opportunity to perform 1/f noise research under his supervision. For providing software solutions for the purposes of data gathering, I give credit to Alberto Rodriguez. In addition, his experience in the area of noise and measurements was useful to me as he generously brought me up to speed with understanding the fundamentals of noise and proper data representation.
    [Show full text]
  • A Mathematical and Physical Analysis of Circuit Jitter with Application to Cryptographic Random Bit Generation
    WJM-6500 BS2-0501 A Mathematical and Physical Analysis of Circuit Jitter with Application to Cryptographic Random Bit Generation A Major Qualifying Project Report: submitted to the Faculty of the WORCESTER POLYTECHNIC INSTITUTE in partial fulfillment of the requirements for the Degree of Bachelor of Science by _____________________________ Wayne R. Coppock _____________________________ Colin R. Philbrook Submitted April 28, 2005 1. Random Number Generator Approved:________________________ Professor William J. Martin 2. Cryptography ________________________ 3. Jitter Professor Berk Sunar 1 Abstract In this paper analysis of jitter is conducted to determine its suitability for use as an entropy source for a true random number generator. Efforts are taken to isolate and quantify jitter in ring oscillator circuits and to understand its relationship to design specifications. The accumulation of jitter via various methods is also investigated to determine whether there is an optimal accumulation technique for sampling the uncertainty of jitter events. Mathematical techniques are used to analyze the accumulation process and an attempt at modeling a signal with jitter is made. The physical properties responsible for the noise that causes jitter are also briefly investigated. 2 Acknowledgements We would like to thank our faculty advisors and our mentors at GD, without whom this project would not have been possible. Our advisors, Professor Bill martin and Professor Berk Sunar, were indispensable in keeping us focused on the tasks ahead as well as for providing background to help us explore new questions as they arose. Our mentors at GD were also key to the project’s success, and we owe them much for this.
    [Show full text]
  • Improving Speech Quality for Hearing Aid Applications Based on Wiener Filter and Composite of Deep Denoising Autoencoders
    signals Article Improving Speech Quality for Hearing Aid Applications Based on Wiener Filter and Composite of Deep Denoising Autoencoders Raghad Yaseen Lazim 1,2 , Zhu Yun 1,2 and Xiaojun Wu 1,2,* 1 Key Laboratory of Modern Teaching Technology, Ministry of Education, Shaanxi Normal University, Xi’an 710062, China; [email protected] (R.Y.L.); [email protected] (Z.Y.) 2 School of Computer Science, Shaanxi Normal University, No.620, West Chang’an Avenue, Chang’an District, Xi’an 710119, China * Correspondence: [email protected] Received: 10 July 2020; Accepted: 1 September 2020; Published: 21 October 2020 Abstract: In hearing aid devices, speech enhancement techniques are a critical component to enable users with hearing loss to attain improved speech quality under noisy conditions. Recently, the deep denoising autoencoder (DDAE) was adopted successfully for recovering the desired speech from noisy observations. However, a single DDAE cannot extract contextual information sufficiently due to the poor generalization in an unknown signal-to-noise ratio (SNR), the local minima, and the fact that the enhanced output shows some residual noise and some level of discontinuity. In this paper, we propose a hybrid approach for hearing aid applications based on two stages: (1) the Wiener filter, which attenuates the noise component and generates a clean speech signal; (2) a composite of three DDAEs with different window lengths, each of which is specialized for a specific enhancement task. Two typical high-frequency hearing loss audiograms were used to test the performance of the approach: Audiogram 1 = (0, 0, 0, 60, 80, 90) and Audiogram 2 = (0, 15, 30, 60, 80, 85).
    [Show full text]
  • Enhanced-SNR Impulse Radio Transceiver Based on Phasers Babak Nikfal,Studentmember,IEEE, Qingfeng Zhang, Member, IEEE,Andchristophe Caloz, Fellow, IEEE
    778 IEEE MICROWAVE AND WIRELESS COMPONENTS LETTERS, VOL. 24, NO. 11, NOVEMBER 2014 Enhanced-SNR Impulse Radio Transceiver Based on Phasers Babak Nikfal,StudentMember,IEEE, Qingfeng Zhang, Member, IEEE,andChristophe Caloz, Fellow, IEEE Abstract—The concept of signal-to-noise ratio (SNR) enhance- transmitter. The message data, which are reduced in the figure ment in impulse radio transceivers based on phasers of opposite to a single baseband rectangular pulse representing a bit of in- chirping slopes is introduced. It is shown that SNR enhancements formation, is injected into the pulse shaper to be transformed by factors and are achieved for burst noise and Gaussian into a smooth Gaussian-type pulse, , of duration .This noise, respectively, where is the stretching factor of the phasers. An experimental demonstration is presented, using stripline cas- pulse is mixed with an LO signal of frequency , which yields caded C-section phasers, where SNR enhancements in agreement the modulated pulse , of peak power . with theory are obtained. The proposed radio analog signal pro- This modulated pulse is injected into a linear up-chirp phaser, cessing transceiver system is simple, low-cost and frequency scal- and subsequently transforms into an up-chirped pulse, . able, and may therefore be suitable for broadband impulse radio Assuming energy conservation (lossless system), the duration ranging and communication applications. of this pulse has increased to while its peak power has de- Index Terms—Dispersion engineering, impulse radio, phaser, creased to ,where is the stretching factor of the phaser, radio analog signal processing, signal-to-noise ratio. given by ,where and are the duration of the input and output pulses, respectively, is the slope of the group delay response of the phaser (in I.
    [Show full text]
  • Next Topic: NOISE
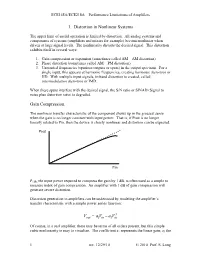
    ECE145A/ECE218A Performance Limitations of Amplifiers 1. Distortion in Nonlinear Systems The upper limit of useful operation is limited by distortion. All analog systems and components of systems (amplifiers and mixers for example) become nonlinear when driven at large signal levels. The nonlinearity distorts the desired signal. This distortion exhibits itself in several ways: 1. Gain compression or expansion (sometimes called AM – AM distortion) 2. Phase distortion (sometimes called AM – PM distortion) 3. Unwanted frequencies (spurious outputs or spurs) in the output spectrum. For a single input, this appears at harmonic frequencies, creating harmonic distortion or HD. With multiple input signals, in-band distortion is created, called intermodulation distortion or IMD. When these spurs interfere with the desired signal, the S/N ratio or SINAD (Signal to noise plus distortion ratio) is degraded. Gain Compression. The nonlinear transfer characteristic of the component shows up in the grossest sense when the gain is no longer constant with input power. That is, if Pout is no longer linearly related to Pin, then the device is clearly nonlinear and distortion can be expected. Pout Pin P1dB, the input power required to compress the gain by 1 dB, is often used as a simple to measure index of gain compression. An amplifier with 1 dB of gain compression will generate severe distortion. Distortion generation in amplifiers can be understood by modeling the amplifier’s transfer characteristic with a simple power series function: 3 VaVaVout=−13 in in Of course, in a real amplifier, there may be terms of all orders present, but this simple cubic nonlinearity is easy to visualize.
    [Show full text]
  • Dithering and Quantization of Audio and Image
    Dithering and Quantization of audio and image Maciej Lipiński - Ext 06135 1. Introduction This project is going to focus on issue of dithering. The main aim of assignment was to develop a program to quantize images and audio signals, which should add noise and to measure mean square errors, comparing the quality of the quantized images with and without noise. The program realizes fallowing: - quantize an image or audio signal using n levels (defined by the user); - measure the MSE (Mean Square Error) between the original and the quantized signals; - add uniform noise in [-d/2,d/2], where d is the quantization step size, using n levels; - quantify the signal (image or audio) after adding the noise, using n levels (user defined); - measure the MSE by comparing the noise-quantized signal with the original; - compare results. The program shows graphic result, presenting original image/audio, quantized image/audio and quantized with dither image/audio. It calculates and displays the values of MSE – mean square error. 2. DITHERING Dither is a form of noise, “erroneous” signal or data which is intentionally added to sample data for the purpose of minimizing quantization error. It is utilized in many different fields where digital processing is used, such as digital audio and images. The quantization and re-quantization of digital data yields error. If that error is repeating and correlated to the signal, the error that results is repeating. In some fields, especially where the receptor is sensitive to such artifacts, cyclical errors yield undesirable artifacts. In these fields dither is helpful to result in less determinable distortions.
    [Show full text]