DOCSLIB.ORG

End-To-End Deep Learning for Phase Noise-Robust Multi-Dimensional Geometric Shaping

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
End-To-End Deep Learning for Phase Noise-Robust Multi-Dimensional Geometric Shaping MITSUBISHI ELECTRIC RESEARCH LABORATORIES https://www.merl.com End-to-End Deep Learning for Phase Noise-Robust Multi-Dimensional Geometric Shaping Talreja, Veeru; Koike-Akino, Toshiaki; Wang, Ye; Millar, David S.; Kojima, Keisuke; Parsons, Kieran TR2020-155 December 11, 2020 Abstract We propose an end-to-end deep learning model for phase noise-robust optical communications. A convolutional embedding layer is integrated with a deep autoencoder for multi-dimensional constellation design to achieve shaping gain. The proposed model offers a significant gain up to 2 dB. European Conference on Optical Communication (ECOC) c 2020 MERL. This work may not be copied or reproduced in whole or in part for any commercial purpose. Permission to copy in whole or in part without payment of fee is granted for nonprofit educational and research purposes provided that all such whole or partial copies include the following: a notice that such copying is by permission of Mitsubishi Electric Research Laboratories, Inc.; an acknowledgment of the authors and individual contributions to the work; and all applicable portions of the copyright notice. Copying, reproduction, or republishing for any other purpose shall require a license with payment of fee to Mitsubishi Electric Research Laboratories, Inc. All rights reserved. Mitsubishi Electric Research Laboratories, Inc. 201 Broadway, Cambridge, Massachusetts 02139 End-to-End Deep Learning for Phase Noise-Robust Multi-Dimensional Geometric Shaping Veeru Talreja, Toshiaki Koike-Akino, Ye Wang, David S. Millar, Keisuke Kojima, Kieran Parsons Mitsubishi Electric Research Labs., 201 Broadway, Cambridge, MA 02139, USA., [email protected] Abstract We propose an end-to-end deep learning model for phase noise-robust optical communi- cations. A convolutional embedding layer is integrated with a deep autoencoder for multi-dimensional constellation design to achieve shaping gain. The proposed model offers a significant gain up to 2 dB. Introduction with codeength scalability and residual PN. The main contributions are summarized below: Due to laser linewidth and fiber nonlinerity, phase 1. We apply DL to joint optimization of both the noise (PN) has been one of the major issues in HDM constellations and DNN demapper in coherent optical communications. To tackle the an E2E framework for optical communication PN issue, there has been a lot of research re- channels. [1] lated to carrier phase estimation and PN-robust 2. We develop a PN-robust E2E model using [2] techniques . For example, modified closed-form convolutional embedding layers, which en- [2],[3] log-likelihood ratio (LLR) calculations have ables scaling to larger code lengths. been proposed to deal with the residual PN. 3. We verify that the E2E model can achieve [4],[5] High-dimensional modulation (HDM) has also high shaping gain close to the Polyanskiy’s shown benefit to mitigate nonlinear PN. bound[14]. Recently, deep learning (DL) has garnered a 4. We demonstrate that the PN-robust E2E can lot of attention in the field of optical communica- offer 2 dB gain in the presence of strong PN. tions. DL has been used for various tasks such as mitigation of fiber nonlinearity[6]–[9], modulation Phase Noise-Robust End-to-End System classification, link quality monitoring, resource al- We implement a typical optical communications location, and end-to-end (E2E) design[10]–[13]. In system including the encoder, the decoder, and many of these advancements, deep neural net- channel as a complete E2E deep neural network works (DNN) have been applied to optimize an with a focus on PN channels as shown in Fig. 1. individual function of the optical communication Unlike the typical E2E methods, the input mes- sub-systems, e.g., coding, modulator, demodula- sage to our embedding layers is not one-hot en- tor, and equalizer. However, such an approach coded, but instead represented as a k-bit vec- may be sub-optimal and therefore, an E2E de- tor x 2 f0; 1gK . This representation of the input sign could be more beneficial for next-generation enables scalability to larger block lengths, while optical communications. E2E method is a novel we introduce a tail-biting convolutional embed- concept that can be utilized to optimize the the ding layer to retain rich encoding capability with transmitter and receiver jointly in interaction with reasonable computational efficiency. This em- the communication channel in an end-to-end pro- bedding layer, parameterized by a dictionary of cess. It was shown that E2E approaches[10]–[13] 2m embedding vectors of length L, maps each can achieve a significant shaping gain in vari- segment of m consecutive bits to an embedding ous fiber-optic systems, by jointly optimizing HDM vector of size L. This embedding layer is cyclically constellation paired with DNN demodulator. applied across the K message bits with a stride However, in most existing E2E literature, one- of one. Then all of the embeddings are concate- hot encoding of the input message is considered, nated vertically to form a vector xe, which is given which limits the practical application to only small as input to the encoder. In our experiments, we codeword lengths. In this paper, we propose an use m = 3 and L = 8. E2E framework optimized for optical communica- The encoder is implemented as a feed forward tions, enabling scalability to larger codelengths as MLP, which consists of an input layer, one hidden well as robustness against PN. Our E2E frame- layer that uses tanh activation and an output layer, work employs tail-biting convolutional embedding followed by a power normalization layer. The in- layers integrated with a deep autoencoder to deal put layer is of size KL, which is equal to that of Hidden Hidden Layer Layer E2E 10-1 Polyanskiy BCH MLD Convolutional Embedding m bits Channel Enc(x ) -2 K bits e y x' 10 x WER AWGN Noise -3 1dB Gain xe 10 xe= K * L Power Normalization Layer Encoder Decoder Fig. 1: Proposed architecture of end to end model. 10-4 3 4 5 6 7 8 9 10 the output of the embedding layer, xe. The output SNR (dB) layer size is N, which effectively yields encoding Fig. 2: AWGN performance for (4,7) codeword. with the parameters (N; K). We use hidden layer E2E 10-1 Polyanskiy size equal to the sum of the input layer and output BCH MLD layer sizes for simplicity. The power normalization is performed with batch normalization (BN), while -2 disabling scale and shift operations. 10 The PN channel is modeled as r = exp(θ)s + WER w, where r is the received symbols vector at the -3 demapper, s is the transmitted symbols vector, 10 θ is the residual PN, which follows the Gaussian 2 distribution of zero mean and variance σρ, and w -4 10 is an additive white Gaussian noise (AWGN) vec- 3 4 5 6 7 8 9 10 tor, whose element follows circularly symmetric SNR (dB) Fig. 3: AWGN performance for (7,15) codeword. complex-Gaussian distribution of zero mean and variance σ2. In coherent optical communications, Hamming distance for (7; 4) codes. Here, we also the PN may come from laser spectrum linewidth, plot the Polyanskiy normal approximation (NA)[14]. fiber nonlinearity, imperfect phase recovery, etc. From the figure, it can be observed that our In the presence of laser linewidth ∆ν, the effec- proposed model outperforms the BCH-MLD by 2 −3 tive PN variance is expressed as σρ = 2π∆νTs nearly 1 dB for a WER of 10 . This suggests that where Ts is the symbol duration. our E2E design can enjoy the geometric shaping The decoder is also implemented as a feed for- gain over the best-known linear coded hyper-cube ward MLP, which consists of an input layer, one modulation. The proposed E2E model also out- hidden layer with tanh activation and an output performs the Polyanskiy’s bound, which is due to layer. The input layer and output layer sizes are the NA being loose for small codeword lengths. equal to N and K, respectively. The hidden layer Fig. 3 shows performance for a (15; 7) code size is equal to the sum of the input layer and out- in AWGN channels. As observed, our pro- put layer sizes. The output layer of decoder uses posed model consistently outperforms MLD per- a sigmoid activation to output a vector x0 repre- formance of the BCH code across all SNRs. We senting the likelihoods for each bit. We use bi- can also observe that performance of our E2E nary cross entropy (BCE) loss to train the E2E model approaches the Polyanskiy NA. network, and hence the DNN output can be di- We verified that our E2E method can achieve rectly fed into a soft-decision FEC without relying excellent performance close to Polyanskiy’s NA in on an external LLR converter. the AWGN channels. We now show the benefit of the E2E design in the PN channels. Fig. 4 shows Performance Analysis the performance of E2E shaping methods with- We evaluated the performance of the proposed /without residual PN. We assume a residual PN 2 E2E system for the AWGN and PN channels. variance of σρ = 0:05, which corresponds to an Fig. 2 compares the word error rate (WER) of our effective linewidth of 239 MHz for 30 GBd. When proposed method for a (7; 4) code in the AWGN E2E is trained at AWGN channels without deal- channel against BCH (7; 4) maximum likelihood ing with the PN, the optimized E2E works well for decoding (MLD). Note that there is no better lin- the AWGN channel as expected, whereas it can ear codes than this BCH code in term of minimum suffer from a significant degradation in the pres- [6] T.
Load more

Recommended publications
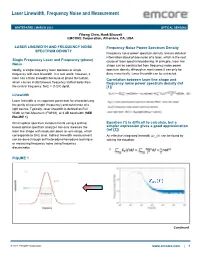
  • Laser Linewidth, Frequency Noise and Measurement
    Laser Linewidth, Frequency Noise and Measurement WHITEPAPER | MARCH 2021 OPTICAL SENSING Yihong Chen, Hank Blauvelt EMCORE Corporation, Alhambra, CA, USA LASER LINEWIDTH AND FREQUENCY NOISE Frequency Noise Power Spectrum Density SPECTRUM DENSITY Frequency noise power spectrum density reveals detailed information about phase noise of a laser, which is the root Single Frequency Laser and Frequency (phase) cause of laser spectral broadening. In principle, laser line Noise shape can be constructed from frequency noise power Ideally, a single frequency laser operates at single spectrum density although in most cases it can only be frequency with zero linewidth. In a real world, however, a done numerically. Laser linewidth can be extracted. laser has a finite linewidth because of phase fluctuation, Correlation between laser line shape and which causes instantaneous frequency shifted away from frequency noise power spectrum density (ref the central frequency: δν(t) = (1/2π) dφ/dt. [1]) Linewidth Laser linewidth is an important parameter for characterizing the purity of wavelength (frequency) and coherence of a Graphic (Heading 4-Subhead Black) light source. Typically, laser linewidth is defined as Full Width at Half-Maximum (FWHM), or 3 dB bandwidth (SEE FIGURE 1) Direct optical spectrum measurements using a grating Equation (1) is difficult to calculate, but a based optical spectrum analyzer can only measure the simpler expression gives a good approximation laser line shape with resolution down to ~pm range, which (ref [2]) corresponds to GHz level. Indirect linewidth measurement An effective integrated linewidth ∆_ can be found by can be done through self-heterodyne/homodyne technique solving the equation: or measuring frequency noise using frequency discriminator.
    [Show full text]
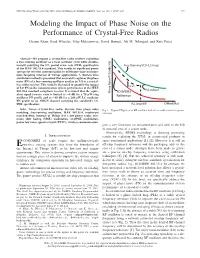
  • Modeling the Impact of Phase Noise on the Performance of Crystal-Free Radios Osama Khan, Brad Wheeler, Filip Maksimovic, David Burnett, Ali M
    IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS—II: EXPRESS BRIEFS, VOL. 64, NO. 7, JULY 2017 777 Modeling the Impact of Phase Noise on the Performance of Crystal-Free Radios Osama Khan, Brad Wheeler, Filip Maksimovic, David Burnett, Ali M. Niknejad, and Kris Pister Abstract—We propose a crystal-free radio receiver exploiting a free-running oscillator as a local oscillator (LO) while simulta- neously satisfying the 1% packet error rate (PER) specification of the IEEE 802.15.4 standard. This results in significant power savings for wireless communication in millimeter-scale microsys- tems targeting Internet of Things applications. A discrete time simulation method is presented that accurately captures the phase noise (PN) of a free-running oscillator used as an LO in a crystal- free radio receiver. This model is then used to quantify the impact of LO PN on the communication system performance of the IEEE 802.15.4 standard compliant receiver. It is found that the equiv- alent signal-to-noise ratio is limited to ∼8 dB for a 75-µW ring oscillator PN profile and to ∼10 dB for a 240-µW LC oscillator PN profile in an AWGN channel satisfying the standard’s 1% PER specification. Index Terms—Crystal-free radio, discrete time phase noise Fig. 1. Typical PN plot of an RF oscillator locked to a stable crystal frequency modeling, free-running oscillators, IEEE 802.15.4, incoherent reference. matched filter, Internet of Things (IoT), low-power radio, min- imum shift keying (MSK) modulation, O-QPSK modulation, power law noise, quartz crystal (XTAL), wireless communication.
    [Show full text]
  • AN279: Estimating Period Jitter from Phase Noise
    AN279 ESTIMATING PERIOD JITTER FROM PHASE NOISE 1. Introduction This application note reviews how RMS period jitter may be estimated from phase noise data. This approach is useful for estimating period jitter when sufficiently accurate time domain instruments, such as jitter measuring oscilloscopes or Time Interval Analyzers (TIAs), are unavailable. 2. Terminology In this application note, the following definitions apply: Cycle-to-cycle jitter—The short-term variation in clock period between adjacent clock cycles. This jitter measure, abbreviated here as JCC, may be specified as either an RMS or peak-to-peak quantity. Jitter—Short-term variations of the significant instants of a digital signal from their ideal positions in time (Ref: Telcordia GR-499-CORE). In this application note, the digital signal is a clock source or oscillator. Short- term here means phase noise contributions are restricted to frequencies greater than or equal to 10 Hz (Ref: Telcordia GR-1244-CORE). Period jitter—The short-term variation in clock period over all measured clock cycles, compared to the average clock period. This jitter measure, abbreviated here as JPER, may be specified as either an RMS or peak-to-peak quantity. This application note will concentrate on estimating the RMS value of this jitter parameter. The illustration in Figure 1 suggests how one might measure the RMS period jitter in the time domain. The first edge is the reference edge or trigger edge as if we were using an oscilloscope. Clock Period Distribution J PER(RMS) = T = 0 T = TPER Figure 1. RMS Period Jitter Example Phase jitter—The integrated jitter (area under the curve) of a phase noise plot over a particular jitter bandwidth.
    [Show full text]
  • AN10062 Phase Noise Measurement Guide for Oscillators
    Phase Noise Measurement Guide for Oscillators Contents 1 Introduction ............................................................................................................................................. 1 2 What is phase noise ................................................................................................................................. 2 3 Methods of phase noise measurement ................................................................................................... 3 4 Connecting the signal to a phase noise analyzer ..................................................................................... 4 4.1 Signal level and thermal noise ......................................................................................................... 4 4.2 Active amplifiers and probes ........................................................................................................... 4 4.3 Oscillator output signal types .......................................................................................................... 5 4.3.1 Single ended LVCMOS ........................................................................................................... 5 4.3.2 Single ended Clipped Sine ..................................................................................................... 5 4.3.3 Differential outputs ............................................................................................................... 6 5 Setting up a phase noise analyzer ...........................................................................................................
    [Show full text]
  • MDOT Noise Analysis and Public Meeting Flow Chart
    Return to Handbook Main Menu Return to Traffic Noise Home Page SPECIAL NOTES – Special Situations or Definitions INTRODUCTION 1. Applicable Early Preliminary Engineering and Design Steps 2. Mandatory Use of the FHWA Traffic Noise Model (TMN) 1.0 STEP 1 – INITIAL PROJECT LEVEL SCOPING AND DETERMINING THE APPROPRIATE LEVEL OF NOISE ANALYSIS 3. Substantial Horizontal or Vertical Alteration 4. Noise Analysis and Abatement Process Summary Tables 5. Controversy related to non-noise issues--- 2.0 STEP 2 – NOISE ANALYSIS INITIAL PROCEDURES 6. Developed and Developing Lands: Permitted Developments 7. Calibration of Noise Meters 8. Multi-family Dwelling Units 9. Exterior Areas of Frequent Human Use 10. MDOT’s Definition of a Noise Impact 3.0 STEP 3 – DETERMINING HIGHWAY TRAFFIC NOISE IMPACTS AND ESTABLISHING ABATEMENT REQUIREMENTS 11. Receptor Unit Soundproofing or Property Acquisition 12. Three-Phased Approach of Noise Abatement Determination 13. Non-Barrier Abatement Measures 14. Not Having a Highway Traffic Noise Impact 15. Category C and D Analyses 16. Greater than 5 dB(A) Highway Traffic Noise Reduction 17. Allowable Cost Per Benefited Receptor Unit (CPBU) 18. Benefiting Receptor Unit Eligibility 19. Analyzing Apartment, Condominium, and Single/Multi-Family Units 20. Abatement for Non-First/Ground Floors 21. Construction and Technology Barrier Construction Tracking 22. Public Parks 23. Land Use Category D 24. Documentation in the Noise Abatement Details Form Return to Handbook Main Menu Return to Traffic Noise Home Page Return to Handbook Main Menu Return to Traffic Noise Home Page 3.0 STEP 3 – DETERMINING HIGHWAY TRAFFIC NOISE IMPACTS AND ESTABLISHING ABATEMENT REQUIREMENTS (Continued) 25. Barrier Optimization 26.
    [Show full text]
  • Analysis of Oscillator Phase-Noise Effects on Self-Interference Cancellation in Full-Duplex OFDM Radio Transceivers
    Revised manuscript for IEEE Transactions on Wireless Communications 1 Analysis of Oscillator Phase-Noise Effects on Self-Interference Cancellation in Full-Duplex OFDM Radio Transceivers Ville Syrjälä, Member, IEEE, Mikko Valkama, Member, IEEE, Lauri Anttila, Member, IEEE, Taneli Riihonen, Student Member, IEEE and Dani Korpi Abstract—This paper addresses the analysis of oscillator phase- recently [1], [2], [3], [4], [5]. Such full-duplex radio noise effects on the self-interference cancellation capability of full- technology has many benefits over the conventional time- duplex direct-conversion radio transceivers. Closed-form solutions division duplexing (TDD) and frequency-division duplexing are derived for the power of the residual self-interference stemming from phase noise in two alternative cases of having either (FDD) based communications. When transmission and independent oscillators or the same oscillator at the transmitter reception happen at the same time and at the same frequency, and receiver chains of the full-duplex transceiver. The results show spectral efficiency is obviously increasing, and can in theory that phase noise has a severe effect on self-interference cancellation even be doubled compared to TDD and FDD, given that the in both of the considered cases, and that by using the common oscillator in upconversion and downconversion results in clearly SI problem can be solved [1]. Furthermore, from wireless lower residual self-interference levels. The results also show that it network perspective, the frequency planning gets simpler, is in general vital to use high quality oscillators in full-duplex since only a single frequency is needed and is shared between transceivers, or have some means for phase noise estimation and uplink and downlink.
    [Show full text]
  • AN-839 RMS Phase Jitter
    RMS Phase Jitter AN-839 APPLICATION NOTE Introduction In order to discuss RMS Phase Jitter, some basics phase noise theory must be understood. Phase noise is often considered an important measurement of spectral purity which is the inherent stability of a timing signal. Phase noise is the frequency domain representation of random fluctuations in the phase of a waveform caused by time domain instabilities called jitter. An ideal sinusoidal oscillator, with perfect spectral purity, has a single line in the frequency spectrum. Such perfect spectral purity is not achievable in a practical oscillator where there are phase and frequency fluctuations. Phase noise is a way of describing the phase and frequency fluctuation or jitter of a timing signal in the frequency domain as compared to a perfect reference signal. Generating Phase Noise and Frequency Spectrum Plots Phase noise data is typically generated from a frequency spectrum plot which can represent a time domain signal in the frequency domain. A frequency spectrum plot is generated via a Fourier transform of the signal, and the resulting values are plotted with power versus frequency. This is normally done using a spectrum analyzer. A frequency spectrum plot is used to define the spectral purity of a signal. The noise power in a band at a specific offset (FO) from the carrier frequency (FC) compared to the power of the carrier frequency is called the dBc Phase Noise. Power Level of a 1Hz band at an offset (F ) dBc Phase Noise = O Power Level of the carrier Frequency (FC) A Phase Noise plot is generated using data from the frequency spectrum plot.
    [Show full text]
  • Non-Stationary Noise Cancellation Using Deep Autoencoder Based on Adversarial Learning
    Non-stationary Noise Cancellation Using Deep Autoencoder Based on Adversarial Learning Kyung-Hyun Lim, Jin-Young Kim, and Sung-Bae Cho(&) Department of Computer Science, Yonsei University, Seoul, South Korea {lkh1075,seago0828,sbcho}@yonsei.ac.kr Abstract. Studies have been conducted to get a clean data from non-stationary noisy signal, which is one of the areas in speech enhancement. Since conven- tional methods rely on first-order statistics, the effort to eliminate noise using deep learning method is intensive. In the real environment, many types of noises are mixed with the target sound, resulting in difficulty to remove only noises. However, most of previous works modeled a small amount of non-stationary noise, which is hard to be applied in real world. To cope with this problem, we propose a novel deep learning model to enhance the auditory signal with adversarial learning of two types of discriminators. One discriminator learns to distinguish a clean signal from the enhanced one by the generator, and the other is trained to recognize the difference between eliminated noise signal and real noise signal. In other words, the second discriminator learns the waveform of noise. Besides, a novel learning method is proposed to stabilize the unstable adversarial learning process. Compared with the previous works, to verify the performance of the propose model, we use 100 kinds of noise. The experimental results show that the proposed model has better performance than other con- ventional methods including the state-of-the-art model in removing non- stationary noise. To evaluate the performance of our model, the scale-invariant source-to-noise ratio is used as an objective evaluation metric.
    [Show full text]
  • This Section Addresses the Potential Noise and Vibration Impacts of The
    4.11 Noise and Vibration 4.11 Noise and Vibration This section addresses the potential noise and vibration impacts of the proposed E&B Oil Development Project, including the development and ongoing operation of the oil drilling and production facility, the truck routes and construction of oil and gas pipelines that would extend out from Hermosa Beach into the cities of Redondo Beach and Torrance and the relocation of the City Yard. It describes the existing noise and vibration environment, identifies significance criteria for noise and vibration impact, assesses the likely impacts of the Project in the context of those criteria and identifies feasible mitigation measures. 4.11.1 Environmental Setting 4.11.1.1 Characteristics of Noise Sound is most commonly experienced by people as pressure waves passing through the air. These rapid fluctuations in air pressure are processed by the human auditory system to produce the sensation of sound. Noise is defined as unwanted sound that may be disturbing or annoying. The character of noise is defined by its loudness and its pitch and also by the way the noise varies with time. Loudness and Sound Level Human perception of loudness is logarithmic rather than linear: On the logarithmic scale, an increase of 10 dB in sound level represents a perceived doubling of loudness. Conversely, a decrease of 10 dB in sound level is perceived as being half as loud. For this reason, sound level is usually measured on a logarithmic decibel (dB) scale, which is calculated from the ratio of the sound pressure to a reference pressure level.
    [Show full text]
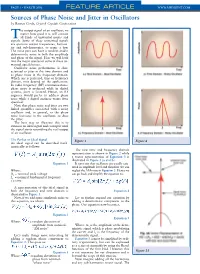
  • Sources of Phase Noise and Jitter in Oscillators by Ramon Cerda, Crystek Crystals Corporation
    PAGE • MARCH 2006 FEATURE ARTICLE WWW.MPDIGEST.COM Sources of Phase Noise and Jitter in Oscillators by Ramon Cerda, Crystek Crystals Corporation he output signal of an oscillator, no matter how good it is, will contain Tall kinds of unwanted noises and signals. Some of these unwanted signals are spurious output frequencies, harmon- ics and sub-harmonics, to name a few. The noise part can have a random and/or deterministic noise in both the amplitude and phase of the signal. Here we will look into the major sources of some of these un- wanted signals/noises. Oscillator noise performance is char- acterized as jitter in the time domain and as phase noise in the frequency domain. Which one is preferred, time or frequency domain, may depend on the application. In radio frequency (RF) communications, phase noise is preferred while in digital systems, jitter is favored. Hence, an RF engineer would prefer to address phase noise while a digital engineer wants jitter specified. Note that phase noise and jitter are two linked quantities associated with a noisy oscillator and, in general, as the phase noise increases in the oscillator, so does the jitter. The best way to illustrate this is to examine an ideal signal and corrupt it until the signal starts resembling the real output of an oscillator. The Perfect or Ideal Signal Figure 1 Figure 2 An ideal signal can be described math- ematically as follows: The new time and frequency domain representation is shown in Figure 2 while a vector representation of Equation 3 is illustrated in Figure 3 (a and b.) Equation 1 It turns out that oscillators are usually satu- rated in amplitude level and therefore we can Where: neglect the AM noise in Equation 3.
    [Show full text]
  • Phase Noise Cancellation in Coherent Communication Systems Using a Radio Frequency Pilot Tone
    applied sciences Article Phase Noise Cancellation in Coherent Communication Systems Using a Radio Frequency Pilot Tone Tianhua Xu 1,2,3,* , Cenqin Jin 2, Shuqing Zhang 4,*, Gunnar Jacobsen 5,6, Sergei Popov 6, Mark Leeson 2 and Tiegen Liu 1 1 Key Laboratory of Opto-Electronic Information Technology (MoE), School of Precision Instruments and Opto-Electronics Engineering, Tianjin University, Tianjin 300072, China; [email protected] 2 School of Engineering, University of Warwick, Coventry CV4 7AL, UK; [email protected] (C.J.); [email protected] (M.L.) 3 Optical Networks Group, University College London, London WC1E 7JE, UK 4 Department of Optical Engineering, Harbin Institute of Technology, Harbin 150001, China 5 NETLAB, RISE Research Institutes of Sweden, SE-16440 Stockholm, Sweden; [email protected] 6 Optics and Photonics Group, KTH Royal Institute of Technology, SE-16440 Stockholm, Sweden; [email protected] * Correspondence: [email protected] (T.X.); [email protected] (S.Z.) Received: 26 September 2019; Accepted: 3 November 2019; Published: 5 November 2019 Featured Application: This work is performed for the compensation of the laser phase noise (LPN) and the equalization enhanced phase noise (EEPN) in high-capacity, long-haul, coherent optical fiber networks. Abstract: Long-haul optical fiber communication employing digital signal processing (DSP)-based dispersion compensation can be distorted by the phenomenon of equalization-enhanced phase noise (EEPN), due to the reciprocities between the dispersion compensation unit and the local oscillator (LO) laser phase noise (LPN). The impact of EEPN scales increases with the increase of the fiber dispersion, laser linewidths, symbol rates, signal bandwidths, and the order of modulation formats.
    [Show full text]
  • Phase Noise Effect on the Minimum Shift Keying Modulator
    AICT 2019 : The Fifteenth Advanced International Conference on Telecommunications Phase Noise Effect on the Minimum Shift Keying Modulator MohammaMahdi Asgharzadeh, Emil Novakov, Ghislaine Maury Institut de Microélectronique, Electromagnétisme et Photonique (IMEP-LAHC) University oF Grenoble Alpes Grenoble, France Email: { mohammad-mahdi.asgharzadeh, emil.novakov, ghislaine.maury}@grenoble-inp.fr Abstract— It is essential to synchronize the receiver and the over a larger band and the receiver sensitivity improvement transmitter during any transmission. In a given receiver, the is related to the spreading factor. sensitivity of the synchronization system is usually higher than Another solution to increase the sensitivity of the receiver the sensitivity of the detection system. The performance of the is to decrease the data rate. Retransmitting the signal and synchronization system and the detection system in a given process it later in the receiver is an example of this method. receiver depends on the signal to noise ratio at the input of the receiver. Phase noise must be carefully considered when This can be viewed as spreading the signal over the time oF applying any signal processing method, which involves the transmission (a time-domain solution). synchronization. The effect of amplitude noise on the sensitivity In [6], the Time Synchronous Averaging (TSA) method of the receiver is a well-studied subject. On the other hand, the is proposed to increase the sensitivity of a digital receiver impact of phase noise on the phase synchronization process is based on the signal retransmission. It is shown that the not well-studied in literature. In this paper, the effect of phase synchronization system limits the performance of the TSA noise on the Minimum Shift Keying (MSK) modulator is method.
    [Show full text]